一个夹角 七种视角 精彩纷呈
——2020年浙江卷高考向量压轴题多维赏析
2022-01-22浙江省海宁市南苑中学314499李安毓
浙江省海宁市南苑中学 (314499) 李安毓
众所周知,浙江卷独特的命题风格对全国卷也有着潜移默化的影响,每年的浙江高考试题八方关注,被研究高考试题的广大师生所青睐.正如2020年浙江卷填空压轴第17题就是一道经典的浙式风格的向量试题,该题入手容易,角度多,突出数学本质.本文就以这道“雅俗共赏”的向量压轴题为例,多角度呈现和品味这道“津津乐道”的好题,以此作为我们日常复习教学中的一个深入浅出的教学素材,与广大数学教师同仁们交流探讨.
一、试题再现,品味经典
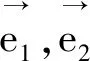
平面向量是沟通代数、几何与三角函数的一种强有力工具,也是高考数学考查的重点知识.纵观近几年《浙江高考考试说明》对此的考试要求都是“理解、掌握、会用”等关键词.然而从平时各种考试情况来看,遗憾的是对学生来说,向量试题由于灵活度大,往往成为他们解题之路难以逾越的鸿沟.此道向量试题作为填空题最后一道压轴题,对学生来讲,背景朴实熟悉,下手容易,有一种似曾相识的感觉.但要真正顺利解出,还是需要具备良好的运算能力与数学推理能力.因此该题是一道命制很完美很具研究价值的一道经典试题.
二、解法赏析
平面向量同时兼具数与形的特征,是数形结合数学思想的完美载体,这意味着向量试题的解放极具多样化.因此,笔者把握机会,对本道高考向量试题的解法进行全方位、多视角剖析,并对其拓展与探究.教学实践表明,有效地落实“一题多解”是提升学生数学能力的重要途径,教师通过引导学生发散思维,思考与呈现不同解法的同时,充分暴露思维痕迹和过程,从而使学生解题能力得以提升!
1 代数法视角(化归转化,凸显通法)
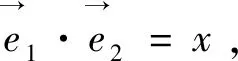
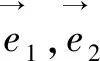
2 坐标法视角(巧妙消元,合理构造)
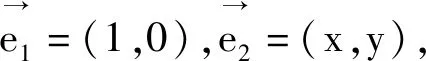
评注:此法的关键是把向量问题坐标化,坐标法是解决向量问题最常用也是最重要的方法之一,学生还是很容易想到和入手,很适合学生的胃口.此法的主要特点是把几何问题代数化,思维起点低,易于操作.但关键要灵活运用消元思想,并要注意到“x”的隐含条件即“x”的范围,最后利用分式函数单调性求解,这一点与解法一相似.
3 三角化处理(三角转化,柳暗花明)

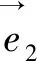
4 基底转化法视角(巧妙转换,简化运算)

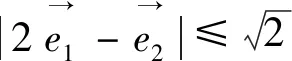
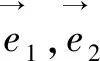
5 平面几何法视角(回到原点,峰回路转)
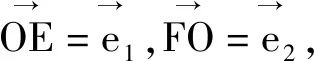

图1
评注:本解法的关键在于以圆为背景,借助向量加法的三角形法则将向量问题几何化.然后巧妙构造ΔAEF的外接圆,进而利用圆周角性质将问题转化为只需求线段GH的最小值即可.其中巧妙灵活应用了初中平面几何知识与锐角三角函数知识将该向量综合问题灵活解决.
6 数形结合法(几何意义,直观具体)
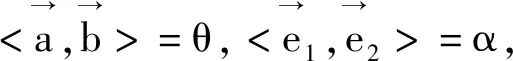
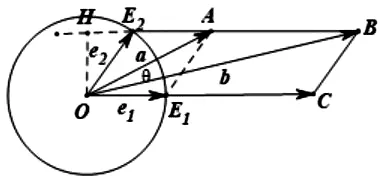
图2
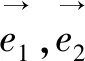
7 介入导数处理(巧用导数,快速求解)
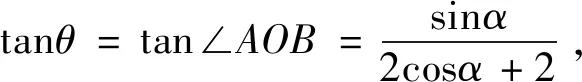
三、追根溯源,品味联系
通过上述对本题命题角度以及解法的研究,笔者发现了好几道与本道浙江高考向量试题的同源题目,它们无论是命题特点还是命题本质都非常接近,给人似曾相识的感觉.以下是笔者收集整理的一些同源变式题,与同行们一起鉴赏和品评一下它们间的内在联系!

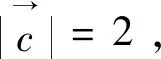
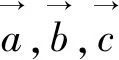


四、探究一般化,结论推广
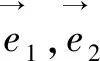
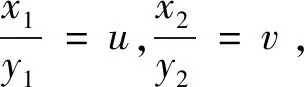
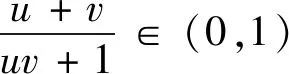
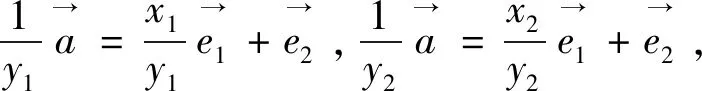
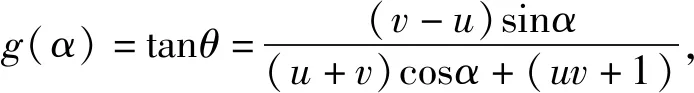

五、教学感悟
每年的高考试题都是高考命题者集体智慧的结晶,高考试题作为载体除了选拔功能更具有很好的教学价值,是一种不可多得的教学素材.本文中笔者正是通过对一道精彩的向量问题从不同层面深入剖析,进行多角度研究和“二次开发利用”,让学生通过一道题明晰一类题,从而使学生认知得到优化、能力得到提升.
向量高考试题一般以平面向量为载体,常常结合其它模块知识如三角函数、解三角形、解析几何等交叉渗透,是高考命题的一个亮点!然而,每年的浙江高考向量试题命制的大都较为新颖,且具有一定难度和技巧,很多考生望而生畏.而2020年这道向量题作为填空压轴题,入口宽解法多,给人似曾相识的感觉,考生无论从那个视角都容易上手,结果也不是很难算.应该说是一道精彩的不可多得的向量好题.在求解过程中,既要将繁琐抽象的代数运算巧妙转化成几何关系,又能对图形性质与特征赋予相应的代数运算,才能使解题事半功倍、游刃有余.
