核心素养视角下几道与球相关的模考题求解赏析*

江西师范大学数学与统计学院 (330022) 梁梦娇

立体几何是高中数学的重要模块内容，近年的高考卷中一般包括一道解答题和两道客观题.而且解答题主要考查学生对传统立体几何求解的一作、二证、三求等三个步骤要求的掌握情况，其中能较好考查到学生直观想象、逻辑推理、数学运算等核心素养.相应地，两道客观题的考查背景中以球为模型出现的频数较高，本文例析几道与球相关的模考题，赏析其在核心素养视角下的求解方法.

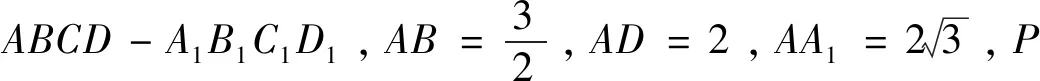
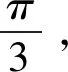
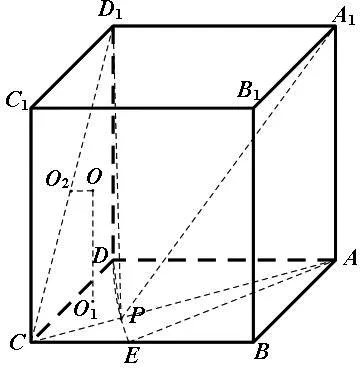
图1

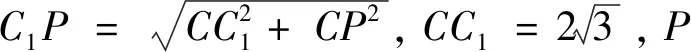
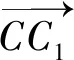
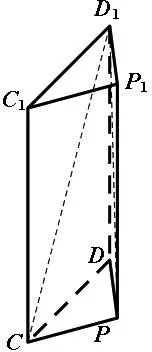
图2

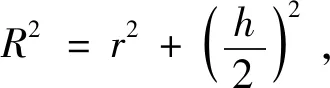
赏析：本题第二问的解法1为定义法，通过分别作三棱锥底面和某一侧面的外心的垂线，进而确定了外接球球心位置，考查学生直观想象、逻辑推理等核心素养.解法2为补体法，它将三棱锥补体成三棱柱，将三棱锥外接球半径问题转化为三棱柱外接球半径，体现了转化思想，考查学生直观想象素养.解法3为公式法，它直接利用已知的半径公式简单快速的解决问题，考查学生数学运算素养.

例2 (2021年江苏省新高考基地学校大联考试卷16题)已知等边△ABC的边长为2，点D,E分别在边AC,BC上，且DE//AB，将ΔCDE沿DE折起，则四棱锥C-DABE的体积的最大值为________，此时四棱锥C-DABE的外接球的表面积为________.

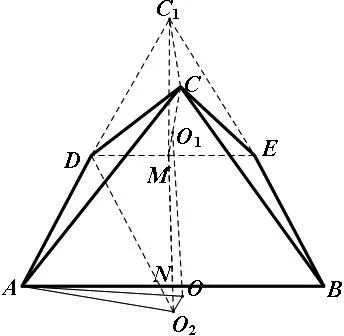
图3

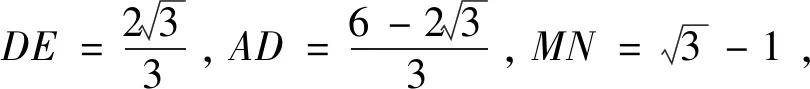
赏析：本题第一问先用翻折角度的三角函数表示出四棱锥的高，确定高的最大值，再设值，用三次函数表示出四棱锥的体积，求导后利用函数单调性求最值问题，其中运用了数形结合、转化与化归及函数与方程等思想方法，能综合考查学生的逻辑推理、数学建模及数学运算等核心素养.

例3 (2021年江苏省六校适应性试卷16题)在长方体ABCD-A1B1C1D1中，AB=13,AD=5,AA1=12,过点A且与直线CD平行的平面α将长方体分成两部分，现同时将两个球分别放入这两部分几何体内，则在平面α变化的过程中，这两个球的半径之和的最大值为________.

解析：如图4，在长方体ABCD-A1B1C1D1中，过点A且与直线CD平行的平面α既有可能与平面CDD1C1相交，也有可能与平面A1B1C1D1相交.由对称性可知，平面α无论与哪个平面相交，两球半径之和的最大值都是相同的，故解答仅考虑平面α与平面CDD1C1相交于直线MN的情况.

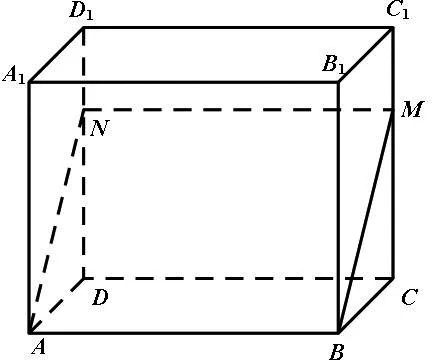
图4

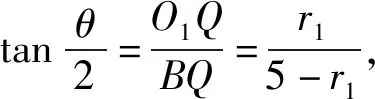
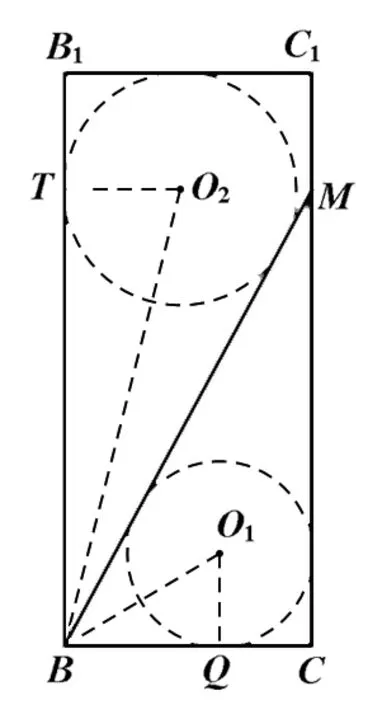
图5

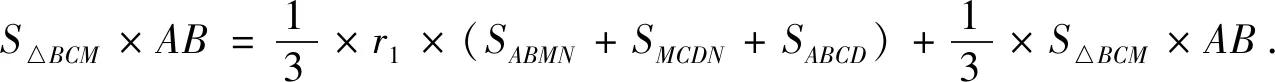
赏析：由求解可知，题中的长方体内两球半径之和与二面角M-AB-C有关，关键是达到构建以二面角为自变量再半径之和为因变量的函数模型，再通过求函数最值达到解决本题最值问题，求解中考查学生数学抽象、数学建模等核心素养.解法1通过作轴截面，将空间中球的半径问题转化为平面内圆的半径问题，降低了思维难度，体现了平面化思想，考查学生直观想象素养.解法2用等体积法，将棱柱分割成几个棱锥，利用几何体等体积的性质，求出球半径，体现了整体转化部分的思想，考查学生逻辑推理、数学运算等核心素养.

用上述三道例题的求解可以发现，在核心素养视角下，以球为模型的客观题不再是单一的考查几何体外接球的表面积和体积，它还会与轨迹、翻折、函数等问题相结合，这样能更好地考查学生的核心素养.