一类带有p-Laplacian算子的分数阶积分边值问题的正解与逐次迭代方法
2022-01-19王文霞段佳艳郭晓珍
王文霞, 段佳艳, 郭晓珍
(太原师范学院数学系, 山西 晋中 030619)
1.引言
由于分数阶微积分在物理学、生物学及工程学等众多领域中的广泛应用, 近年来分数阶微分方程理论得到了广泛而深入的研究[1−3].作为非牛顿力学、弹性理论等诸多研究领域中的重要数学模型,带有p-Laplacian算子的分数阶微分方程受到越来越多的关注[4−6].文[7]研究了如下带有p-Laplacian算子的Riemann-Liouville型分数阶边值问题

其中2< α ≤3, 1< β ≤2, 0< ξ <1, λ ≥0,φp(s) =|s|p−2s,p >1.应用锥上的不动点理获得了上述边值问题至少存在一个和两个正解的充分条件.文[8]运用单调迭代技术研究了如下带有p-Laplacian算子的Riemann-Liouville型分数阶微分方程边值问题

正解的存在性, 其中1<α,γ ≤2,β >0,1+β ≤α, 0<ξ,η <1,φp(s)=|s|p−2s,p>1.
受上述文献的启迪, 本文将研究如下带有p-Laplacian算子并且非线性项f中含有分数阶导数项的分数阶微分方程的积分边值问题(简记为BVP)


众所周知, 使用单调迭代方法研究边值问题解的存在性时, 需要以边值问题的上下解作为迭代序列的初值.特别的, 当使用该方法研究带有p-Laplacian算子且非线性项f中含有分数阶导数项的分数阶边值问题解的存在性时, 所获结论中通常都会把“边值问题存在上解以及下解”作为假设条件, 见文[9-10]及其参考文献.但是本文并不需要这样的假设条件.
2.预备知识
定义2.1[11]函数y:(0,+∞)→R的α>0 阶Riemann-Liouville分数阶积分为

只要上式右端在(0,+∞)有定义; 连续函数y: (0,+∞)→R的α >0阶Riemann-Liouville分数阶导数为

只要上式右端在(0,+∞)有定义, 其中n=min{m ∈Z|m ≥α},Γ(α)为Gamma函数.
引理2.1[11]设α>0,u ∈C(0,1)∩L(0,1),(0,1)∩L(0,1),则
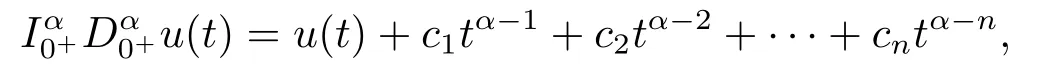
其中n=min{m ∈Z|m ≥α},ci ∈R,i=1,2,··· ,n.
引理2.2设y ∈C[0,1], 则分数阶微分方程边值问题

有唯一解

其中

证由以及引理2.1可得,等价于

进而等价于


可得

于是BVP(2.1)的唯一解为

证毕.
为了方便,记

引理2.3引理2.2中的G1(t,s)与G(t,s)满足如下性质:
(i)G(t,s)在[0,1]×[0,1]上连续;
(ii) 0≤G1(t,s)≤t,s ∈[0,1];
(iii) 0≤G(t,s)≤γtα−1≤γ, t,s ∈[0,1].
证由G(t,s)和G1(t,s)的表达式易知结论(i)和(ii)成立.
以下证明结论(iii).对于任意的t,s ∈[0,1], 显然有G(t,s)≥0.另一方面, 由结论(ii)可得

故结论(iii)成立.证毕.
3.主要结果
设X={u ∈C[0,1][0,1]}.对任意的u ∈X, 定义其范数为

容易证明X是为Banach空间.再令
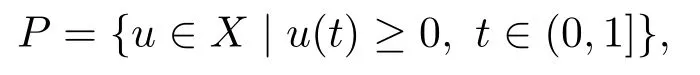
则P是X中的锥.定义算子T如下:对任意的u ∈P,

根据引理2.2的证明容易看到

引理3.1算子T:P →P是全连续算子.
证根据引理2.3及函数h(t),f(t,x)的非负连续性容易证明T:P →P是连续算子.以下证明T为紧算子.为此设Ω是锥P中的有界集.注意到f,h的非负连续性,于是存在正数W >0使得
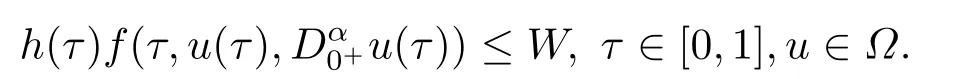
进而对任意的u ∈Ω, 由引理2.3有
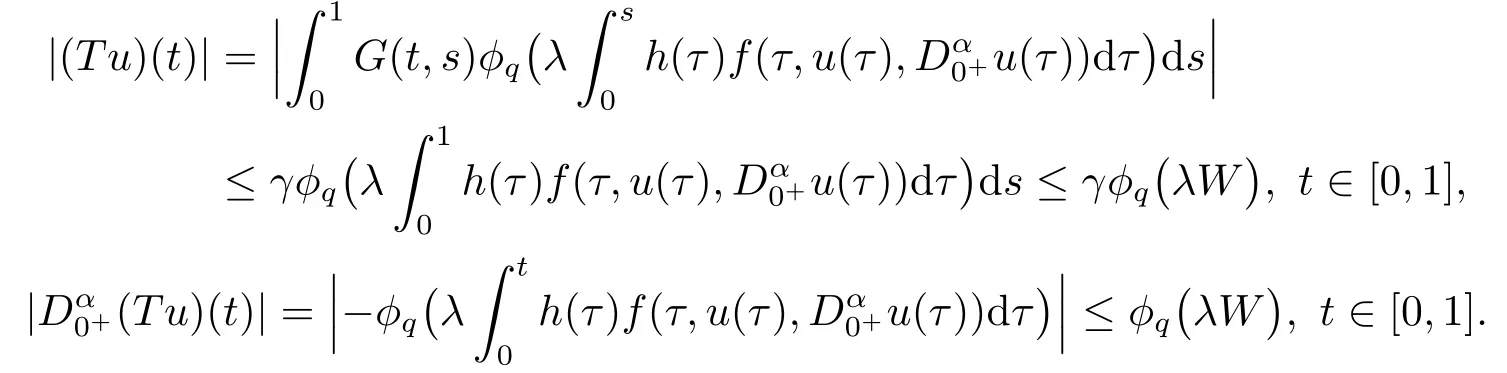
由此可知T(Ω)和)|u ∈Ω}皆为C[0,1]中一致有界的子集合.
再证T(Ω)和(Tu)|u ∈Ω}皆为C[0,1]中等度连续的子集合.对任意的0≤t1 既然G(t,s)在[0,1]×[0,1]上连续,从而一致连续性,故T(Ω)为C[0,1]中等度连续的子集合.此外, 考虑两种情况: (i) 当0 进而有 (ii) 当q −1≥1时, 根据拉格朗日中值定理可知, 存在ξ ∈(t1,t2)使得 进而有 这样, 由(3.1)式和(3.2)式可知(Tu)|u ∈Ω}亦为C[0,1]中等度连续的子集合. 既然集合T(Ω)和(Tu)|u ∈Ω}都是一致有界且等度连续的,根据Arzela-Ascoli定理可知T(Ω)和)|u ∈Ω}皆为C[0,1]中的相对紧集,进而可知T是全连续算子.证毕. 记 定理3.1若以下两个条件成立: (H1)f(t,0,0)在[0,1]上不恒为零, 且存在a>0, 使得 (H2) 对任意的0≤t ≤1,0≤u1≤u2≤a,0≤|v1|≤|v2|≤a有f(t,u1,v1)≤f(t,u2,v2).则BVP(1.1)存在正解v∗及u∗, 且满足0<‖v∗‖≤‖u∗‖≤a, 以及 其中 满足 证令Pa={u ∈P | ‖u‖≤a},则对任意的u ∈Pa有 于是由条件(H1)及(H2)可得 进而由引理2.3有 所以‖Tu‖≤a, 此即 取 则 故 此外, 根据引理2.3, 条件(H1), (H2)及(3.7)式得 此即 以此类推 再注意到 于是由引理3.1知{un |n=1,2,···}是中的列紧集, 于是存在u∗∈使得 进而由算子T的连续性以及un=Tun−1可得u∗=Tu∗, 即u∗是算子T在中的不动点.此外, 由引理2.2可知,x ∈P是T的不动点当且仅当x为BVP(1.1)在P中的解, 故u∗是BVP(1.1)的非负解.既然f(t,0,0)在[0,1]上不恒为零,h(t)在[0,1]上大于零, 于是u(t)>0,t ∈(0,1),即u∗是BVP(1.1)的正解, 且满足0<‖u∗‖≤a以及(3.4)式. 再取v0(t)≡0, 显然v0令 进而由(H2)得 以此类推 此即(3.3)式成立. 此外, 注意到 有 以此类推 由(3.8)-(3.12)式可知, 迭代序列{un},{vn}及BVP(1.1)的正解u∗和v∗还满足(3.5)式和(3.6)式,进而有0<‖v∗‖≤‖u∗‖≤a.证毕. 考虑如下带有p-Laplacian算子的分数阶微分方程边值问题 此即在BVP(1.1)中,p=3,α=η=1, 计算可得 选取a=32, 则有 故条件(H1)成立.此外由f的表达式易知, 对任意的0≤t ≤1,0≤u1≤u2≤32,0≤|v1| ≤|v2| ≤32 有f(t,u1,v1)≤f(t,u2,v2), 此即条件(H2)成立.于是根据定理3.1, BVP(4.1)存在正解v∗及u∗满足0<‖v∗‖≤‖u∗‖≤32, 以及 其中 (n=1,2,···) 满足定理3.1中的(3.5)式和(3.6)式.
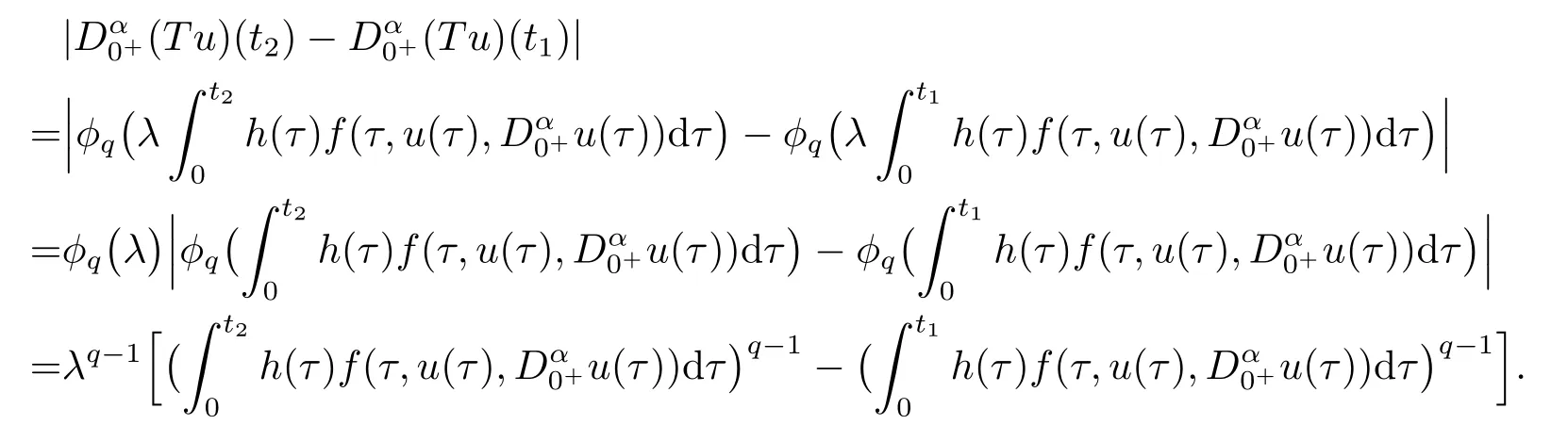
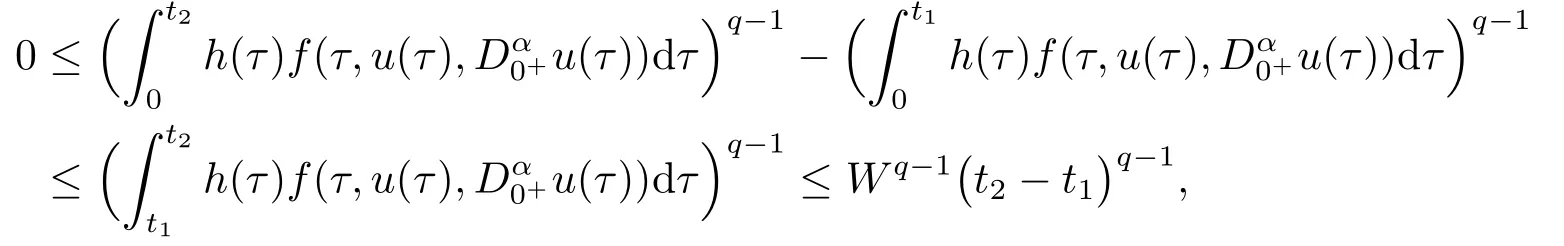

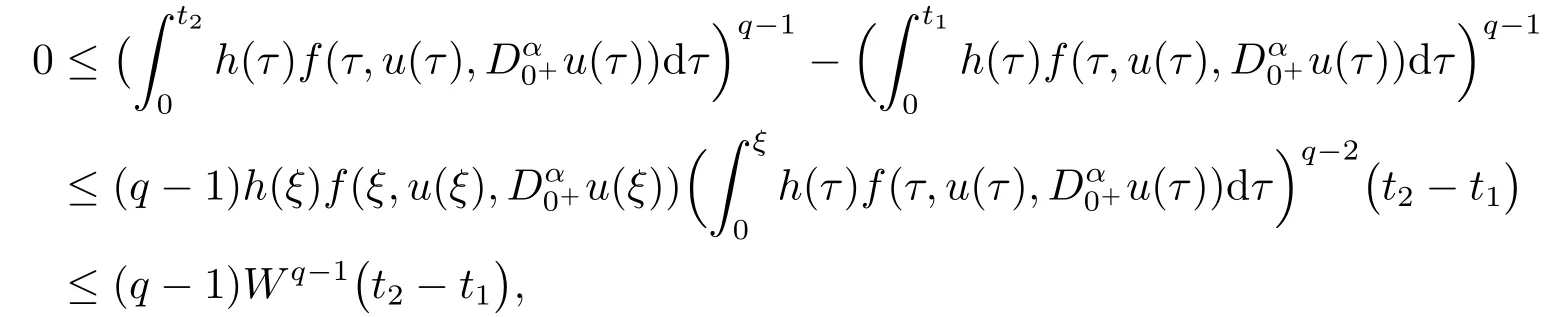




















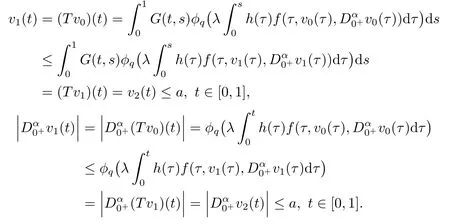

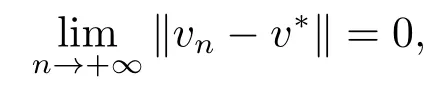




4.例







猜你喜欢
杂志排行
应用数学的其它文章
- Atomic Decomposition of Weighted Orlicz-Lorentz Martingale Spaces and Its Applications
- Solvability of Mixed Fractional Periodic Boundary Value Problem with p(t)-Laplacian Operator
- 一类含Hardy-Leray势的分数阶p-Laplacian方程解的单调性和对称性
- 一类非线性趋化方程的能控性及时间最优控制
- Existence of Positive Solutions for a Fractional Differential Equation with Multi-point Boundary Value Problems
- 奇异椭圆方程Robin问题多重正解的存在性
