奇异椭圆方程Robin问题多重正解的存在性
2022-01-19吴德科索洪敏
吴德科, 索洪敏
(贵州民族大学数据科学与信息工程学院, 贵州 贵阳 550025)
1.引言
本文考虑如下奇异椭圆方程Robin边值问题非平凡解的存在性:

其中Ω ⊂RN(N ≥3)是光滑有界区域, 2< p <2∗,2∗=是Sobolev临界指数, 0< γ <1,参数λ>0, 0≤a(x)∈L∞(∂Ω)是一个非负函数,n为外法向单位向量.
文[1-6] 研究了如下奇异的Dirichlet边值问题:

其中Ω ⊂RN(N ≥3)是光滑有界区域,0<γ <1,参数λ>0.当指数1
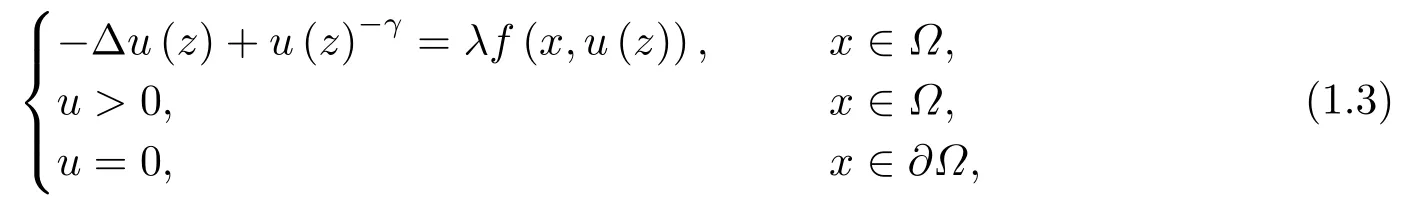
其中Ω ⊂RN(N ≥3)是光滑有界区域, 0< γ <1, 参数λ >0,f:Ω ×R→R是一个Carathodory函数.利用变分法证明了存在一个临界参数λ∗, 当λ > λ∗时, 问题(1.3)至少存在两个非平凡解, 当0<λ<λ∗时, 问题(1.3)无解.
2014年, 文[8]考虑已下奇异的Neumann边值问题:
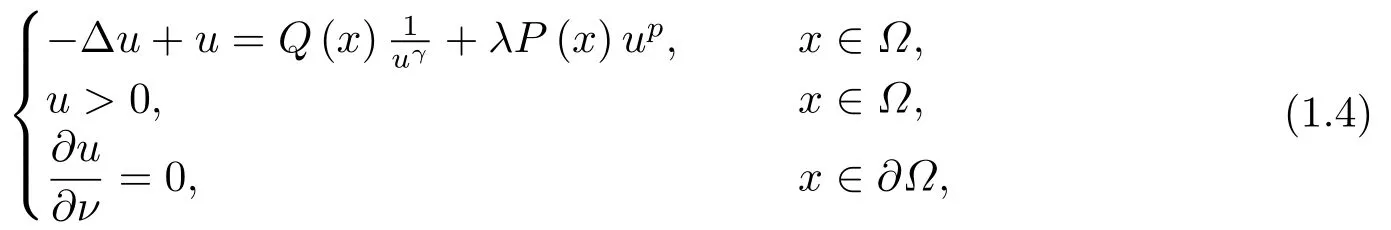
其中Ω ⊂RN(N ≥3)是光滑有界区域, 1
受以上文献启发, 本文拟研究问题(1.1) 非平凡解的存在性与多重性.主要思路: 首先运用Nehari流形方法解决带奇异项问题所对应泛函在零点处不可微的难点, 其次应用Ekeland变分原理得到该问题对应泛函存在的临界点, 最后通过极大值原理得到两个正解的存在性.本文的主要结果如下:
定理1.1假设0 < γ < 1, 2 < p < 2∗, a(x) ∈L∞(∂Ω)为非负函数, 则存在一个常数Λ∗>0, 使得对任意的λ ∈(0,Λ∗), 问题(1.1)至少存在两个正解u1,u2∈H1(Ω).
2.准备工作
问题(1.1)对应的变分泛函Iλ:H1(Ω)→R为

众所周知, 奇异项导致泛函Iλ不属于C1(H1(Ω),R).然而, 我们可以通过研究泛函Iλ的合适的最小化问题来获得问题(1.1)的多重解.
记Sp为Sobolev最佳嵌入常数, 且

若u>0, u ∈H1(Ω)且满足

就称u是问题(1.1) 的弱解.
定义纤维映射:
Φ:t →Iλ(tu)(t>0).
当u ∈H1(Ω)时,
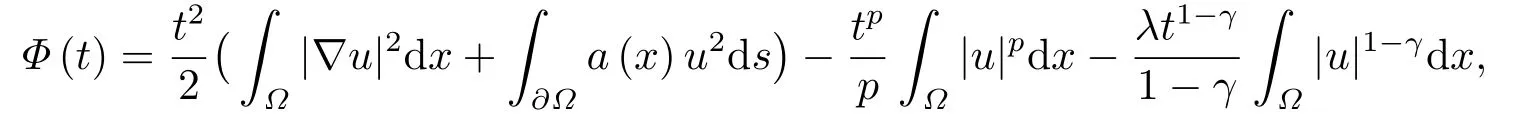
上式关于t求一阶导数和二阶导数, 可得
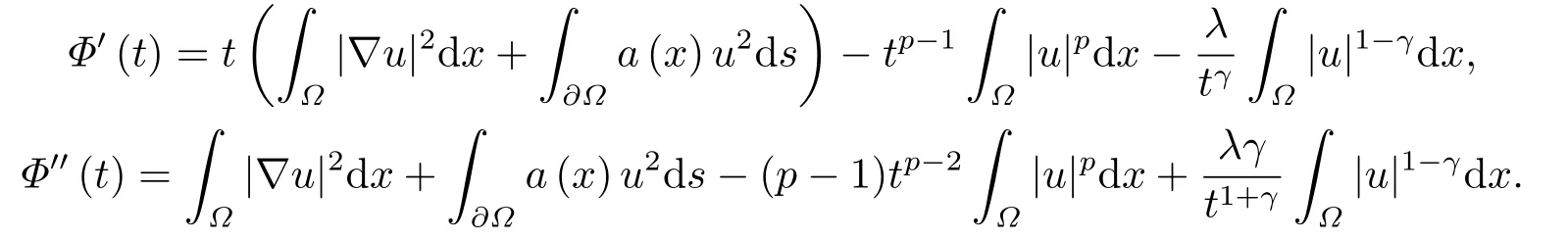
令t=1, 可得
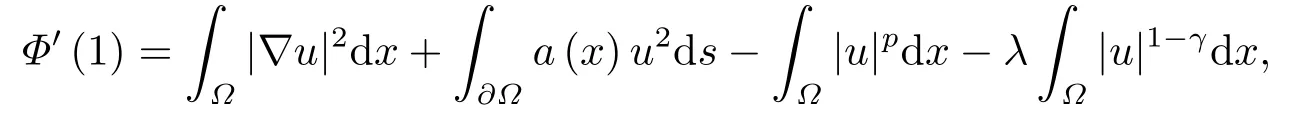
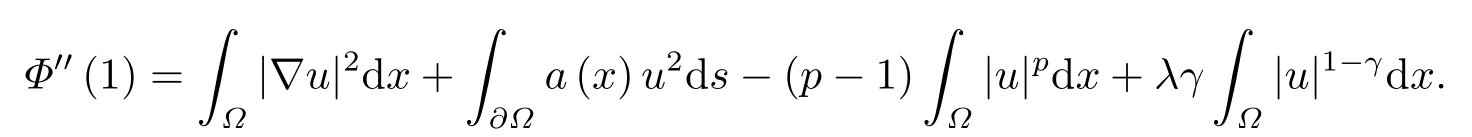
问题(1.1)对应的Nehari流形为
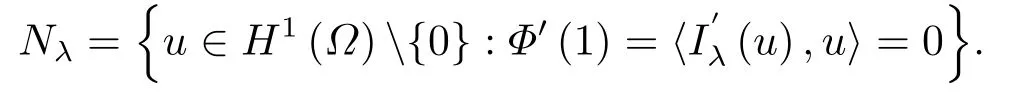
因此,Nλ包含了问题(1.1)所有的非零弱解, 即对任意的u ∈Nλ当且仅当
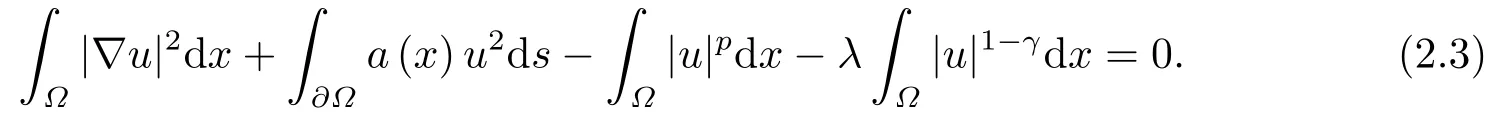
然而当t>0,u ∈H1(Ω){0}, 可得到

通过(2.3)和(2.4), 显然可得Φ′(t) = 0当且仅当tu ∈Nλ.可直接验证Φ′(1) = 0等价于u ∈Nλ.现在, 把Nλ划分为三个部分

当u ∈Nλ时, 可得

3.定理1.1的证明
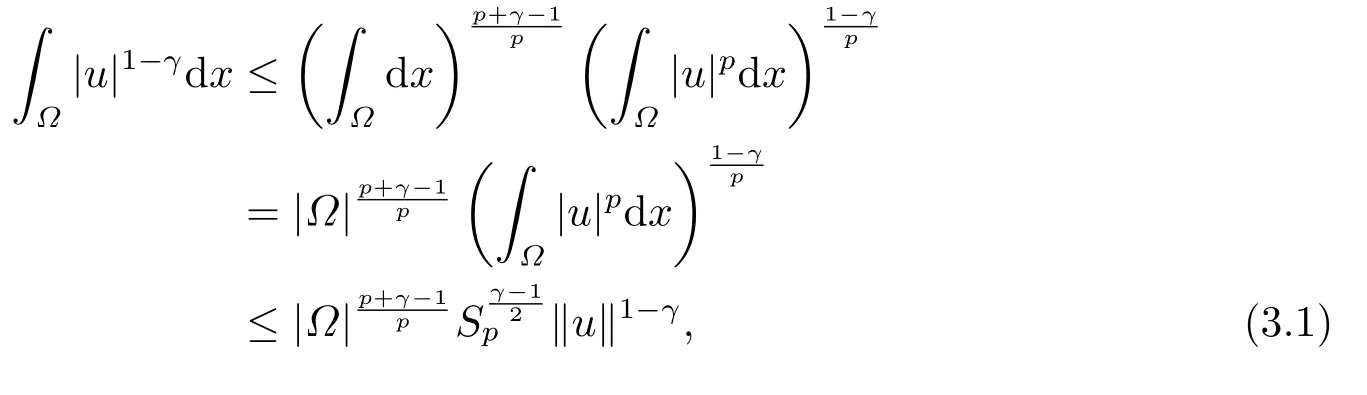
和

这里0<γ <1, 2 引理3.1[9](迹定理) 设1≤p ≤∞,Ω是有界域且∂Ω是C1的光滑边界, 则存在一个有界线性算子 使得 (i)Tu=u|∂Ω,若 (ii)‖Tu‖Lp(∂Ω)≤C‖u‖W1,p(Ω), 其中C是仅与p和Ω有关的常数. 根据引理3.1, 可得 证(i) 当u ∈H1(Ω){0}时, 依据(2.4)式可得 定义Q(t)∈C(R+,R)有 上式分别对t求一阶导数和二阶导数, 得到 令Q′(t)=0, 有 通过一系列计算, 很容易的算出当0< t < tmax时, 有Q′(t)>0; 当t > tmax时, 有Q′(t)<0.因此显然当t=tmax时, 有Q(t)能取到最大值, 即 通过(3.5), 可得 这里 于是对∀0<λ<λ1, 可得 注意到u0, 有 由(3.7)可得 结合(3.9)和(3.8)可得 一方面, 对u00}, 由不等式这里为了方便使用参数Θ, 利用Sobolev不等式, 可得 另一方面, 当0<λ<λ2时, 有 其中 根据(3.11)式和(3.12)式可得到是矛盾的, 那么, 当0 < λ < λ2时, 有= ∅.除此之外取Λ0=min{λ1,λ2}, 当0<λ<Λ0时, 引理3.2也是成立的. 引理3.3设0<γ <1且0 ≤a(x)∈L∞(∂Ω).则泛函Iλ在Nλ中强制且下方有界. 证当u ∈Nλ时, 利用Sobolev不等式, 可以得到 由于0<γ <1且0 ≤a(x)∈L∞(∂Ω), 因此泛函Iλ在Nλ中强制且下方有界. 根据引理3.2知, 对∀0<λ<Λ0有Nλ=∪成立.此外, 由于和非空, 再依据引理3.3知如下下确界的定义有意义 引理3.4设0<γ <1 且0 ≤a(x)∈L∞(∂Ω).则对任意的0<λ<Λ0都有αλ≤<0. 证当u ∈时, 可得 结合(2.3)式和(3.13)式, 可得 因为0<γ <1且0 ≤a(x)∈L∞(∂Ω), 则Iλ(u)<0.通过αλ和的定义可推出αλ≤<0. 引理3.5设0 < γ < 1且0 ≤a(x) ∈L∞(∂Ω).则存在常数ε > 0及光滑连续可微泛函τ :H1(Ω)→(0,+∞)(也就是τ :ω →τ(ω)>0), 使得对任意的u ∈Nλ(), ω ∈H1(Ω),当‖ω‖<ε时总有 证任给u ∈Nλ, 定义函数F(t,ω):R×H1(Ω)→R为 因u ∈Nλ, 能推出F(1,0)=0且 其中0.通过引理3.2知Ft(1,0)0.进一步, 根据隐函数存在唯一性定理知, 存在常数>0及光滑连续可微函数τ=τ(ω)>0,ω ∈H1(Ω)使得τ(0) = 1且F(τ(ω),ω)≡0, 也就是说 于是, 对任意的ω ∈H1(Ω), 当‖ω‖<时, 有τ(ω)(u+ω)∈Nλ.因此当ε ∈(0,)充分小时, 对任意的ω ∈H1(Ω), 当‖ω‖<ε时, 有τ(ω)(u+ω)∈Nλ. 定理1.1的证明设0<λ<Λ0, 我们将分两部分来完成证明. 第一部分 证明问题(1.1)在存在一个解. 由引理3.3知{un}在H1(Ω)中有界.运用Ekeland变分原理, 则存在Iλ的一个极小化序列{un}⊂Nλ, 使得 显然Iλ(|un|)=Iλ(un).现在假设在Ω上un ≥0, 那么存在一个极小化序列(仍记为{un})和u ∈H1(Ω)有 下面证明u1是问题(1.1)的解. 首先证明在Ω中u10.根据Vitalian定理可以得到 由{un}在H1(Ω)中有界, 可得 根据范数的弱下半连续性, 结合(3.14)式和(3.15) 式, 有 这就意味着:在Ω中u10. 其次, 证明在Ω中几乎处处都有u1(x)>0.由于un ∈N+λ, 所以可以断言存在一个C1>0使得下式成立 事实上, (3.16)式等价于下式 由于un ∈可得 从而, 根据(3.15)式和(3.14)式, 进一步得到 因此, 只需证明下式成立 反证法, 假设下式成立 由 根据范数的弱下半连续性, 结合(3.15)式、(3.14) 式以及(3.19)式, 有 从而, 由(3.6)式, 当0<λ<λ1时, 有 这是矛盾的.因此, (3.18)式成立.在引理3.5中取u=un以及φ ∈H1(Ω),φ ≥0,t>0充分小,可以获得一列连续函数列τn=τ(ω)使得τn(0) = 1以及τn(ω)(un+ωφ)∈Λ+以及un ∈Λ+,可得 从而, 结合(3.20)式, 进一步可得 上式两边同时除以ω >0, 可得 令 类似于文[8]的证明, 可以得到 这里的C2为常数.根据范数的次可加性, 可得 两边同时除以ω, 有 根据(3.20)式, 可得 和 因此, 由(3.24)式, 可得 因为 则根据Fatou引理可得 从而, 结合(3.25)式和(3.23)式, 可推得 当n充分大时, 有 再次利用Fatou引理可得 即 这里φ ∈H1(Ω),φ ≥0.这意味着u1在弱意义上满足 又因为u1≥0且u10, 根据强极大值原理, 可得 接下来, 证明u1∈N+.一方面, 由(3.27)式, 在(3.26)式中选取φ=u1, 可得 另一方面, 有 因此 这就意味:u1∈N.再次利用(3.20)式, 可得 因此, 根据(3.28)式, 可得在空间H1(Ω)当n → ∞时有un → u1.特别地, 结合(3.28)式和(3.18)式, 可得 从而可推得u1∈N+. 最后, 证明u1是问题(1.1)的解.对任意的φ ∈H1(Ω),ε >0, 令Ψ= (u1+εφ)+∈H1(Ω),从而可以将(3.26) 式中的Ψ代替φ.在结合(3.28) 式, 可以得到 这里Ω1={x ∈Ω|u1+εφ>0},Ω2={x ∈Ω|u1+εφ ≤0}, 当ε →0时, 其测度|Ω2|→0, 故有 在(3.30)式的不等式两边同除以ε且让ε →0, 有 在(3.31)式中用−φ来代替, 有 那么 由于φ是任意的, 所以u1是问题(1.1) 的解. 第二部分 证明问题(1.1)在存在一个解, 令Λ∗= min{Λ0,1}.因此, 当0< λ < Λ∗时,引理3.2-3.5都是成立的, 下面分两步来证明. 由于{un}在H1(Ω)上是有界的, 若有必要时取其子列, 故∃u2∈H1(Ω), 使得当n →∞时, 有 同第一个解的证明类似, 可得到u2是问题(1.1)的一个非负解.因un ∈依据(3.2)式可得 可推导出 当n →∞时, 使得在H1(Ω)中,un →u2.这意味着u20.因此, 根据强极大值原理在Ω中有u2>0. 第2步 证明u2由的定义知 当n →∞时, 使得在H1(Ω)中有un →u2.又由(3.35)式可以得出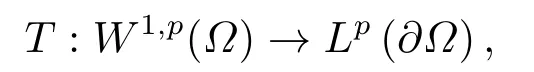
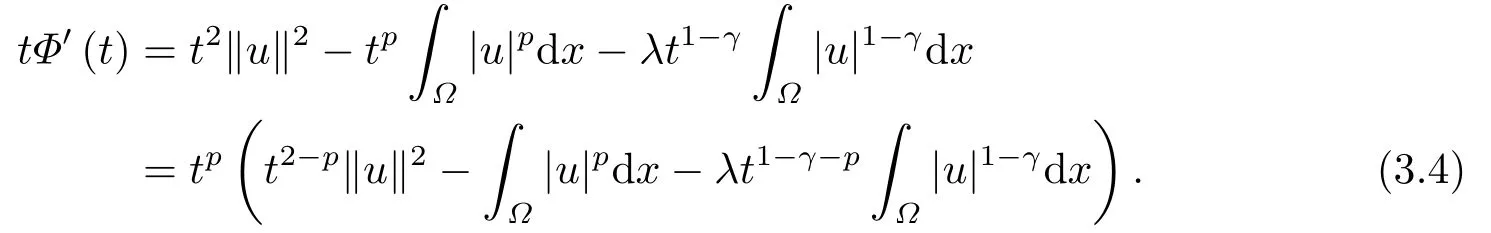

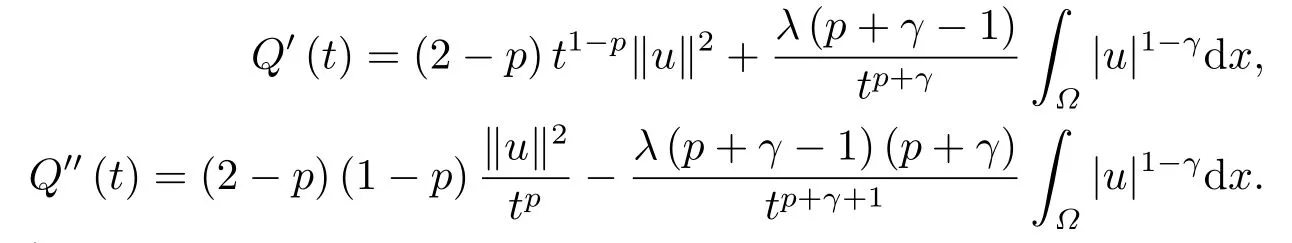
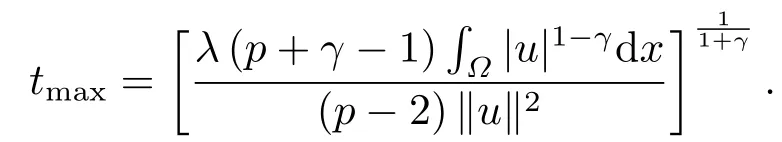
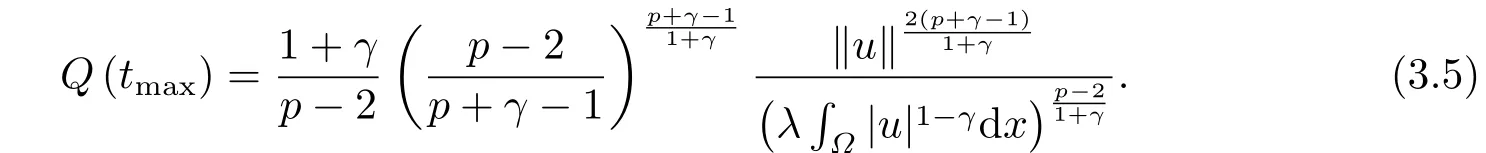

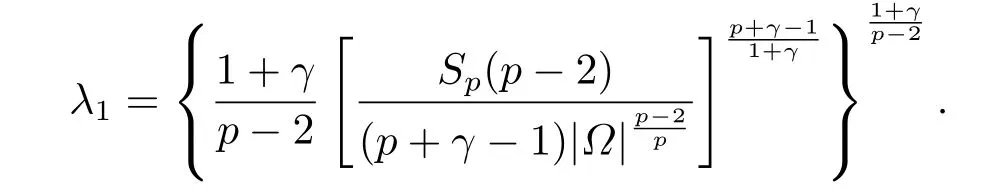


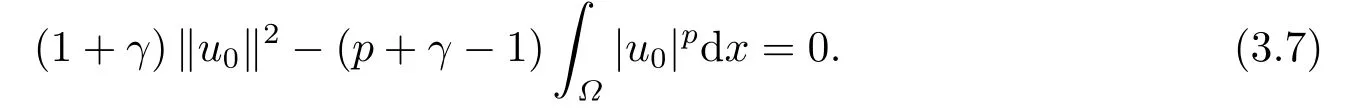

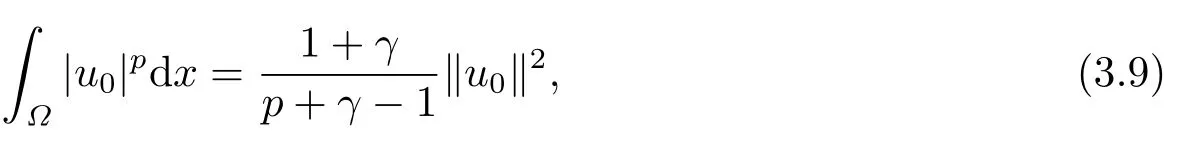
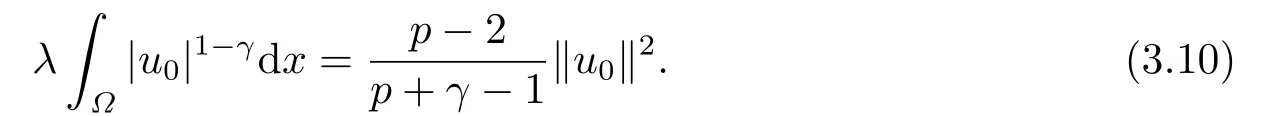

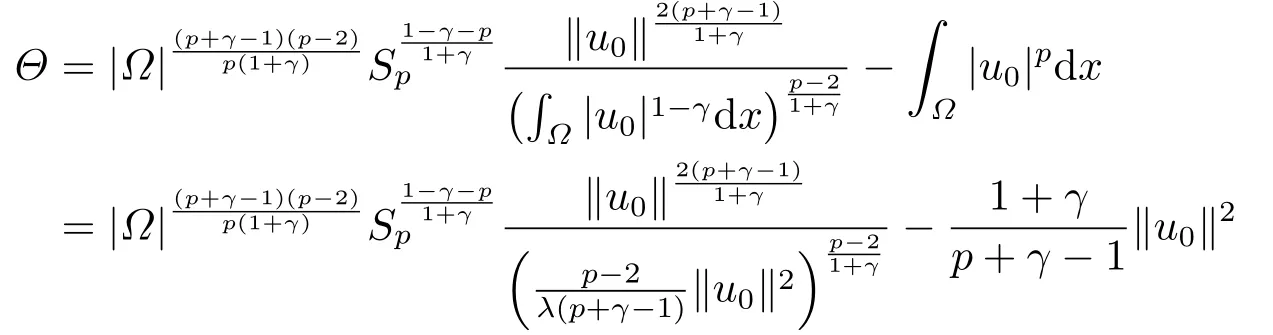
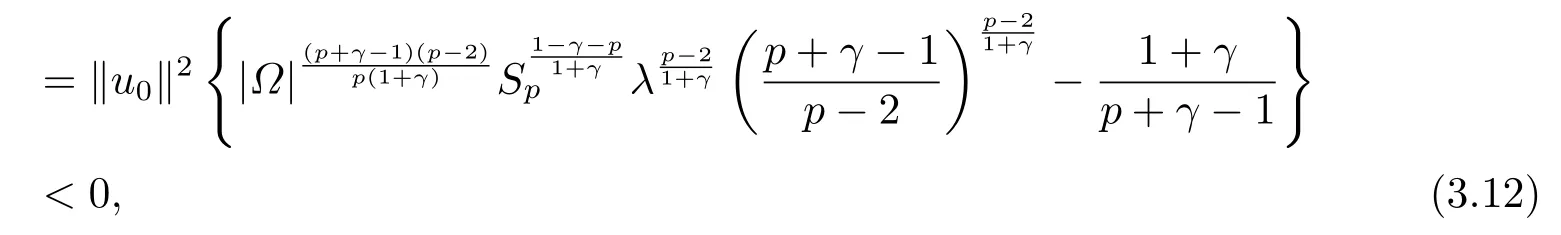
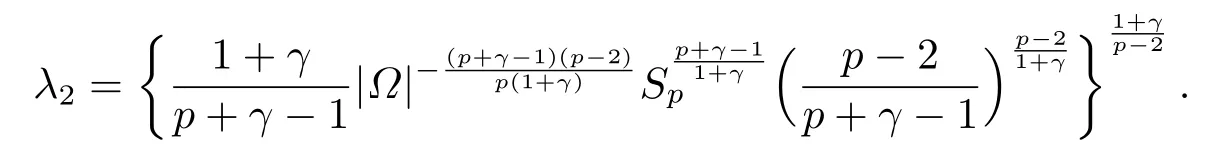
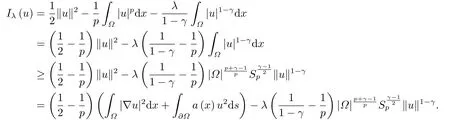
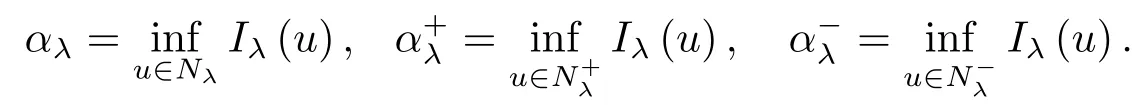

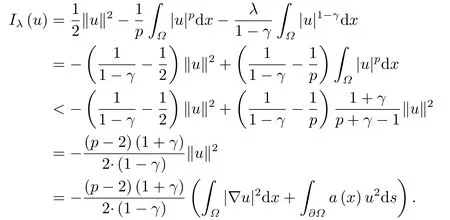

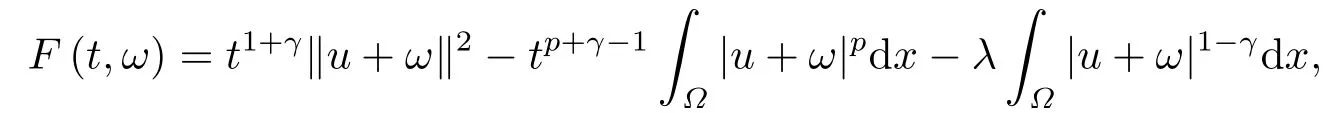
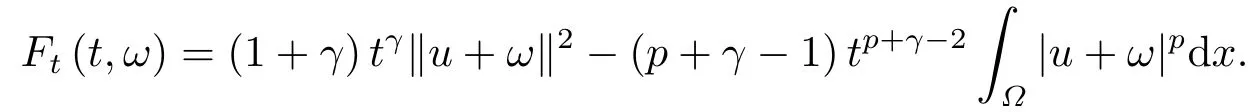
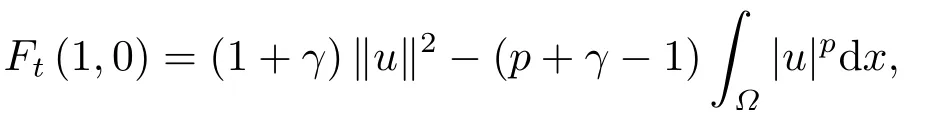
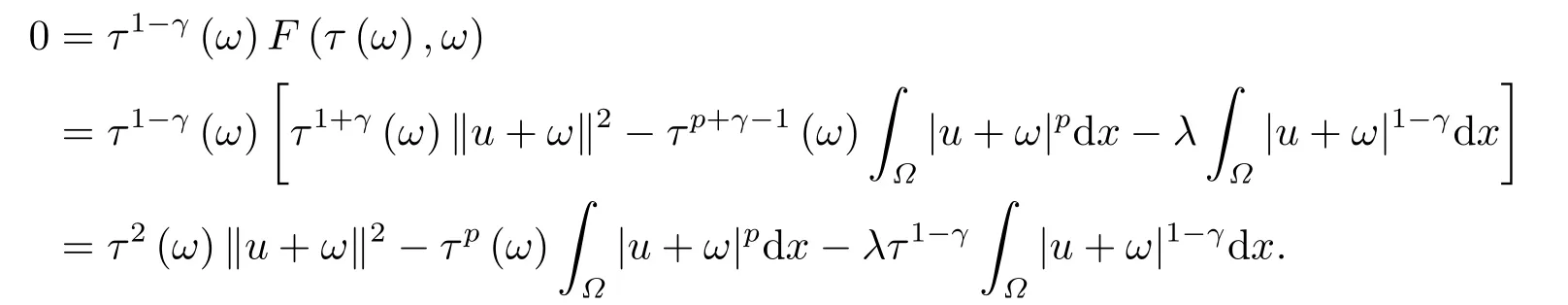
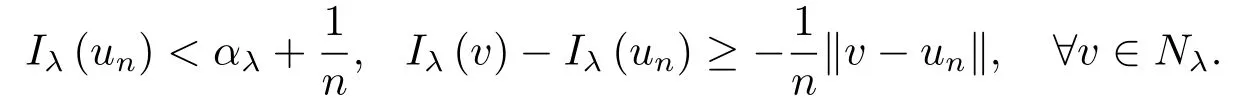
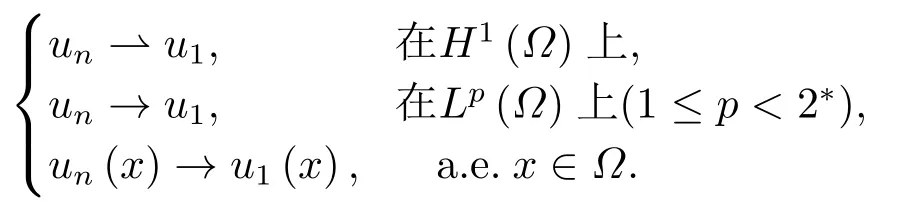
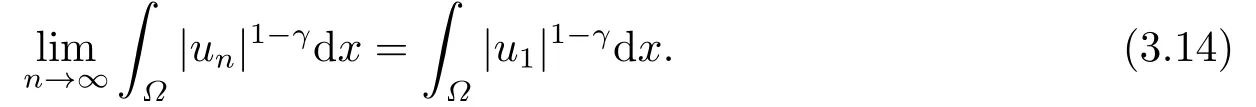
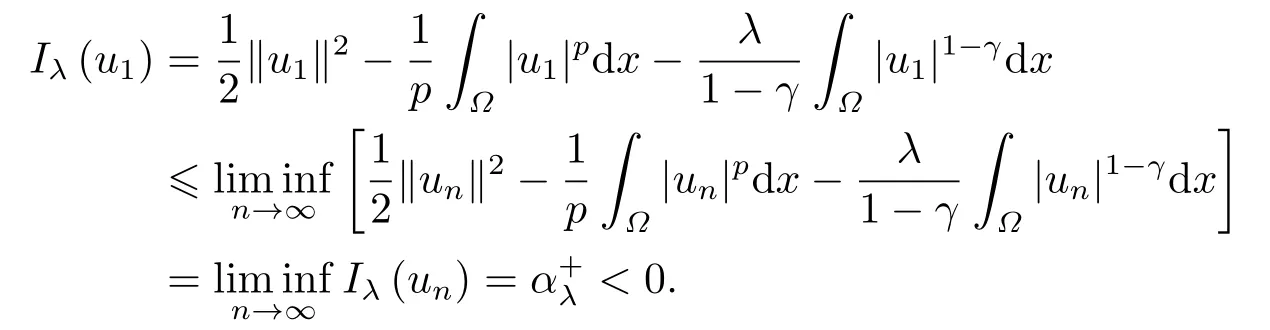

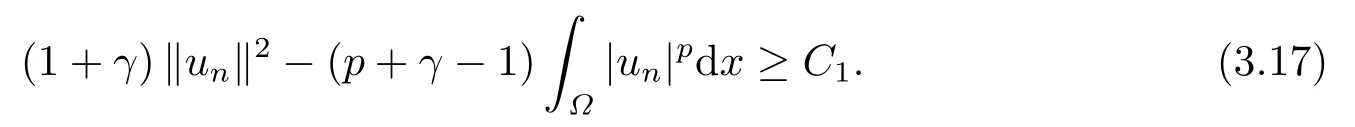


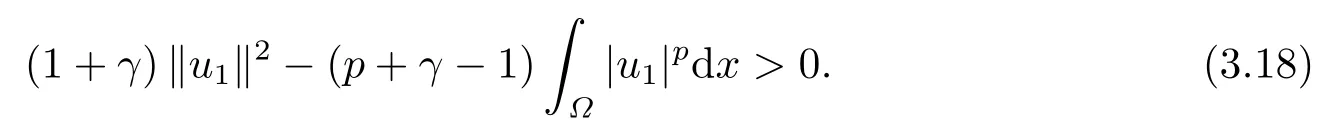
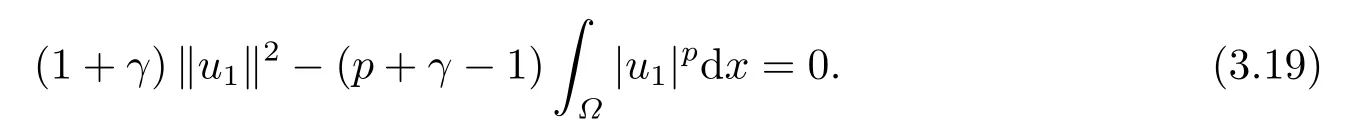
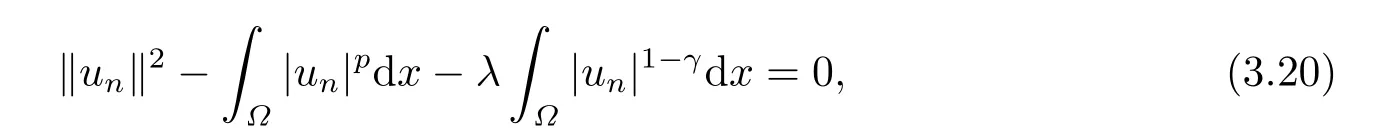
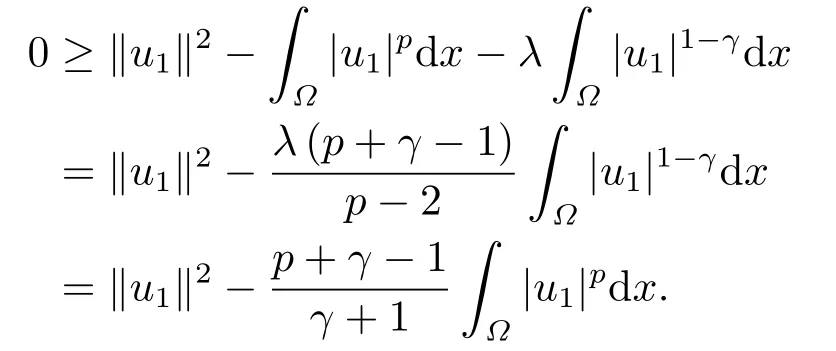

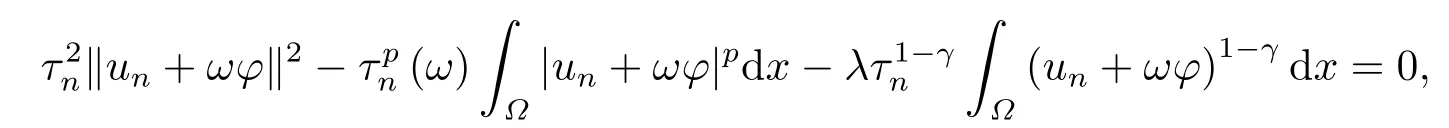
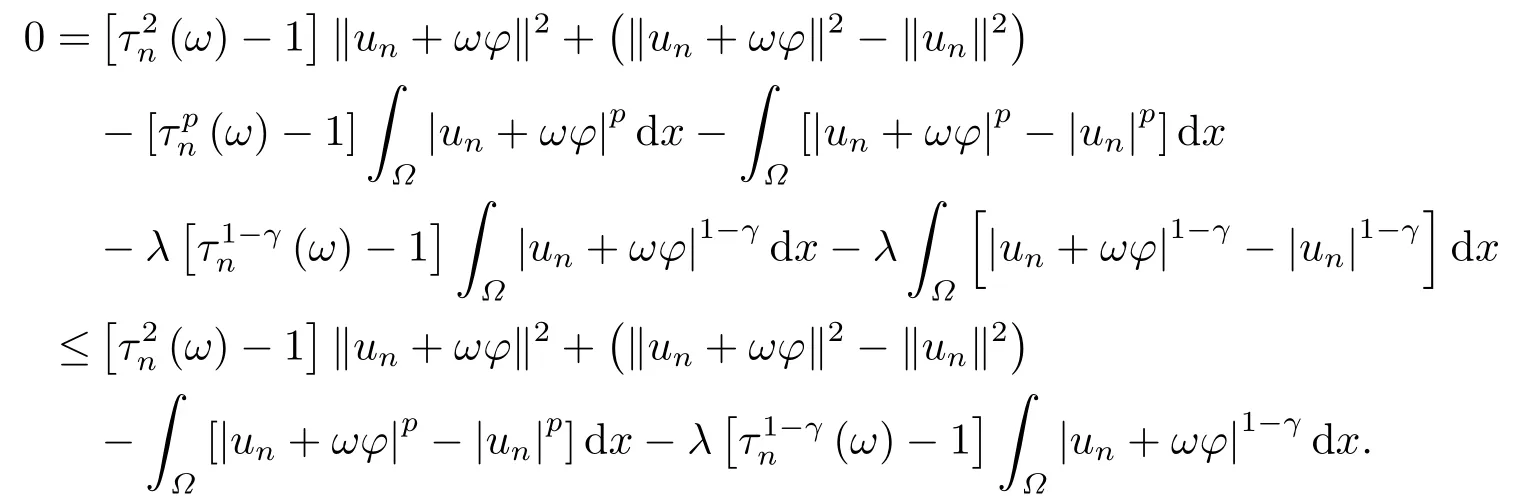
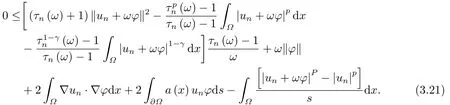


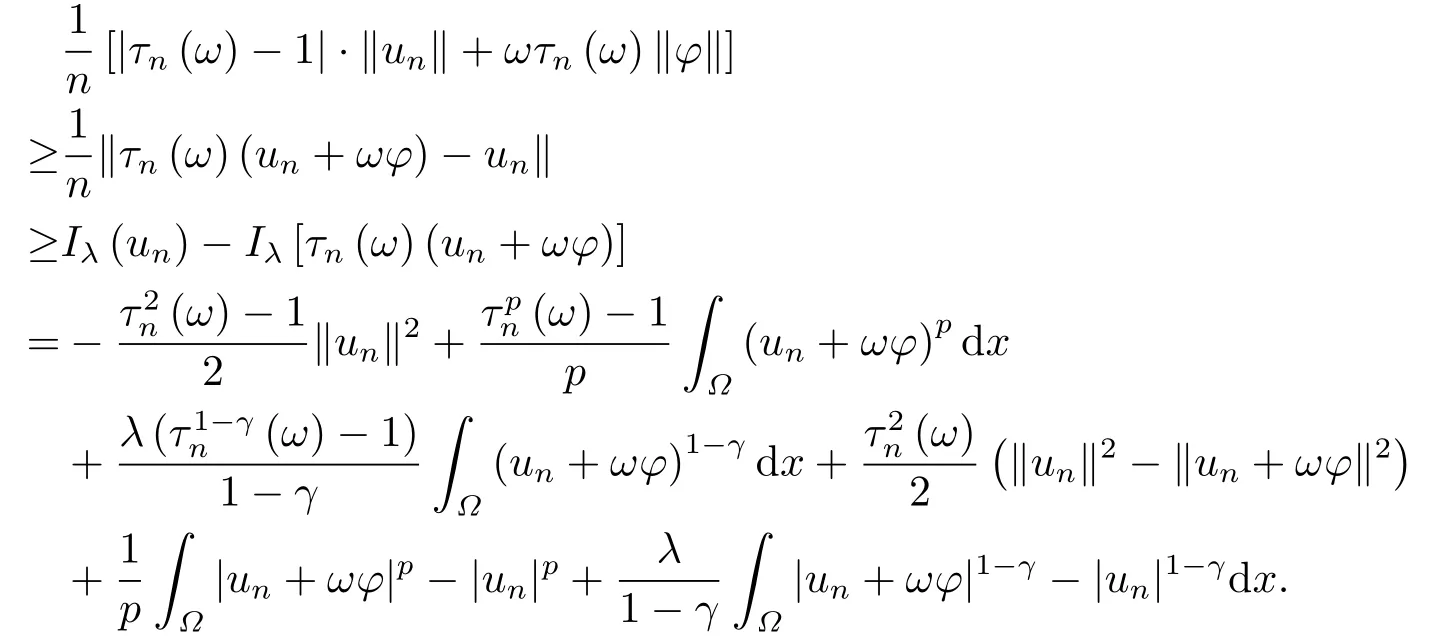
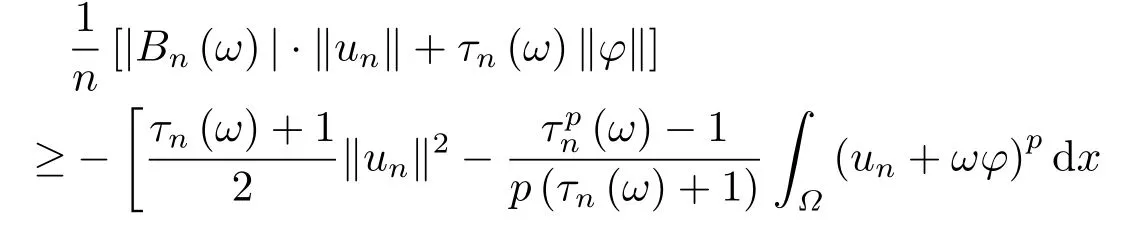
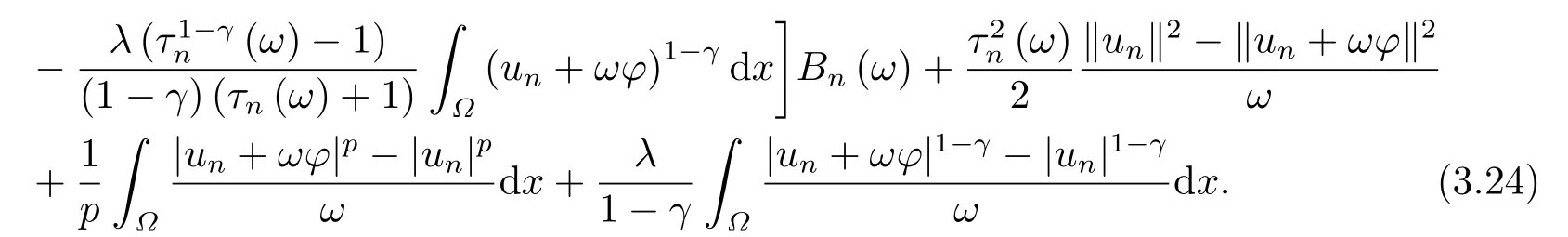
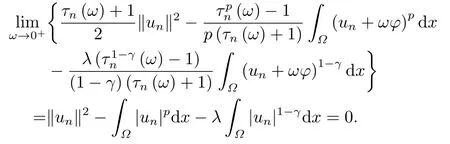

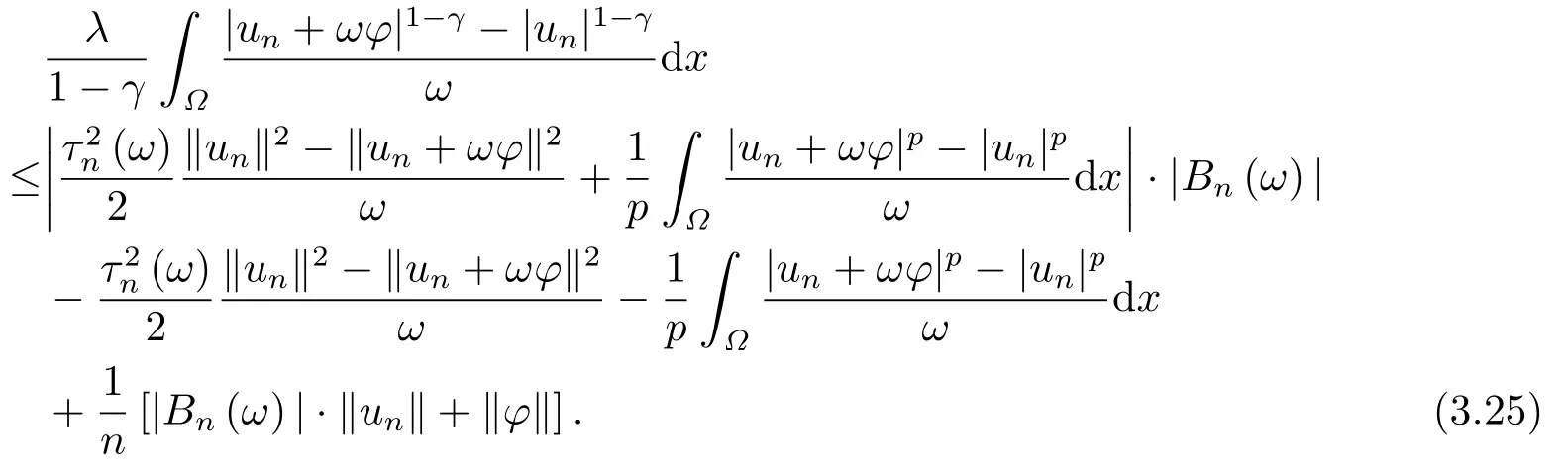
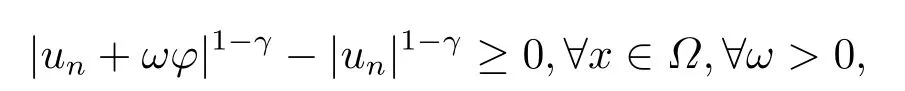
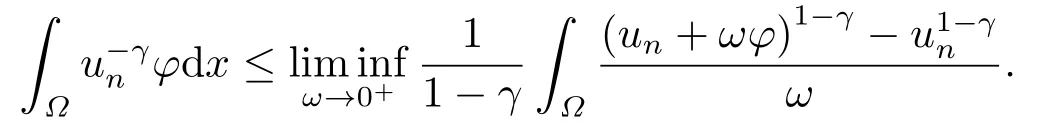
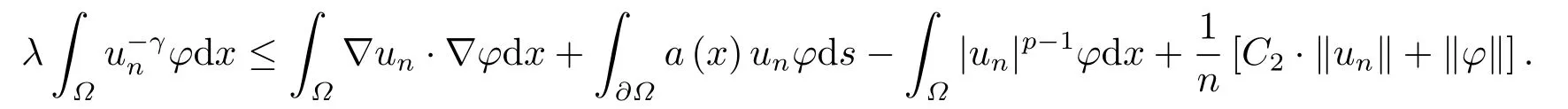
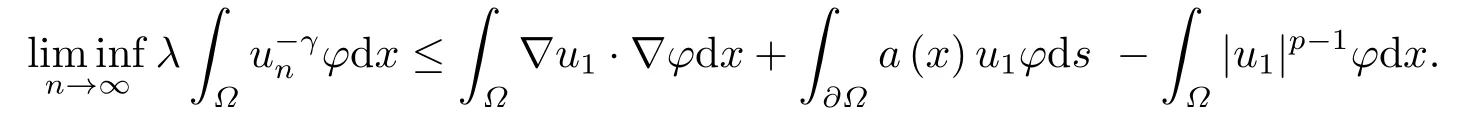
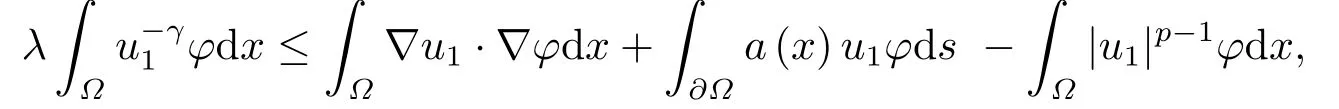
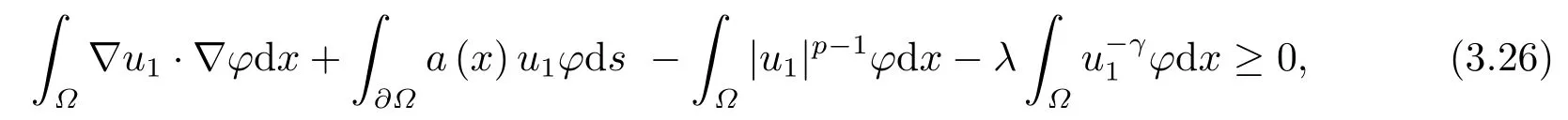
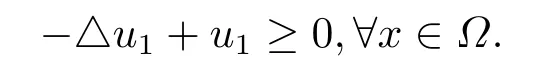



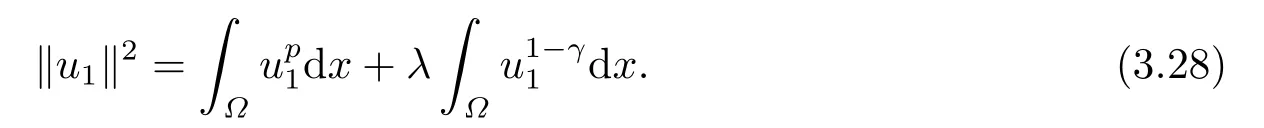
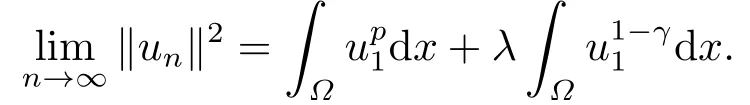
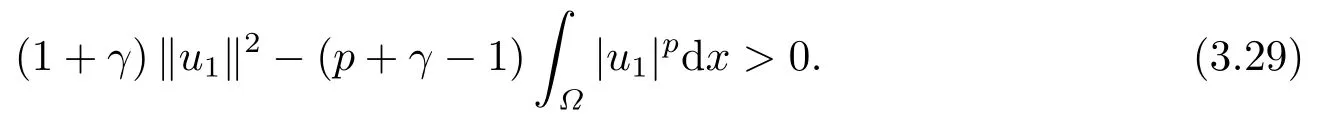
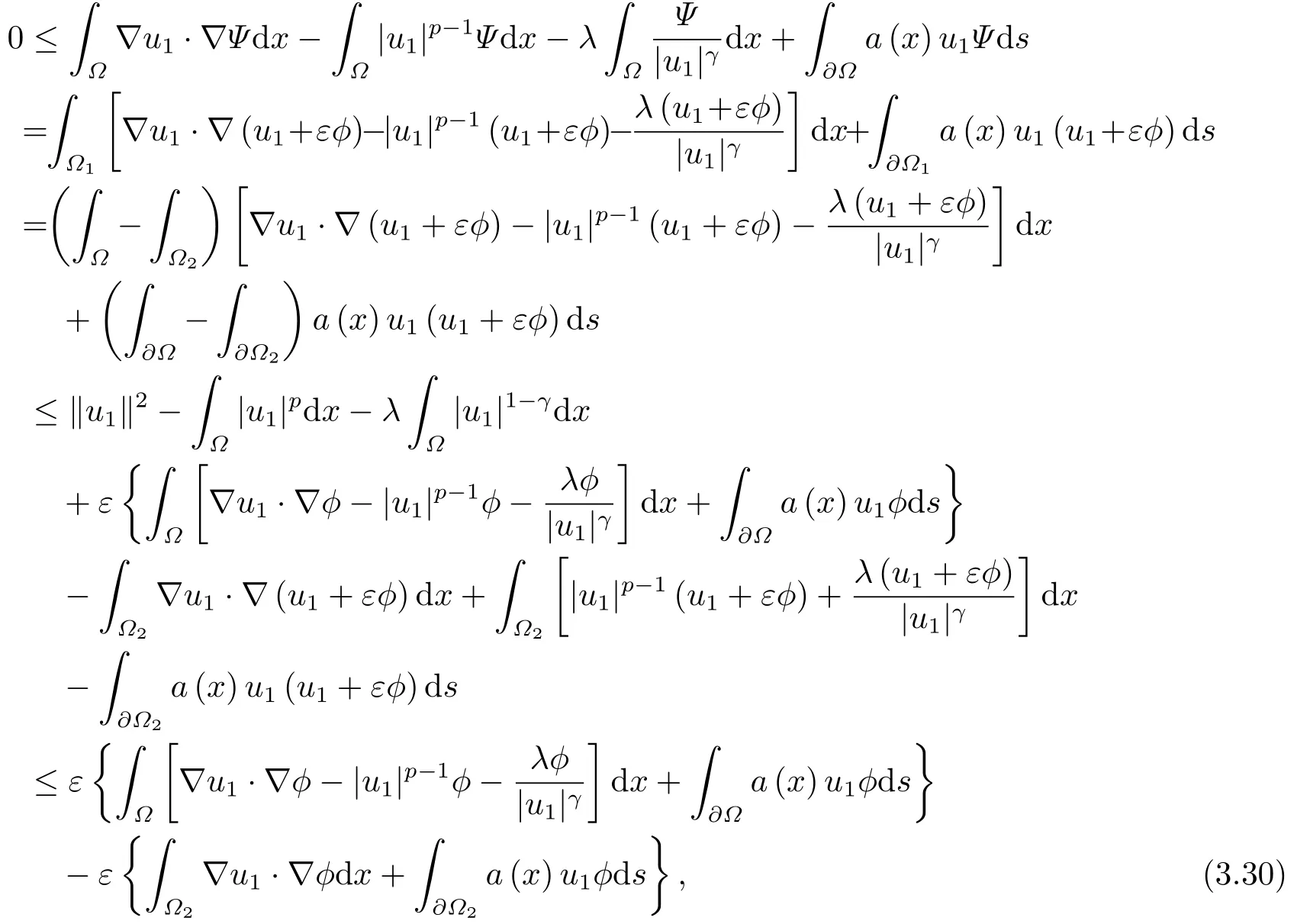
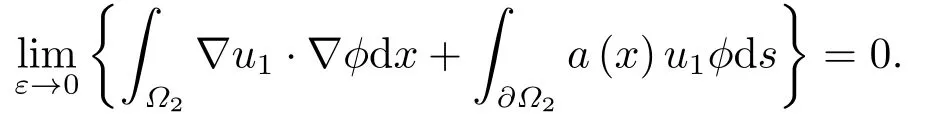

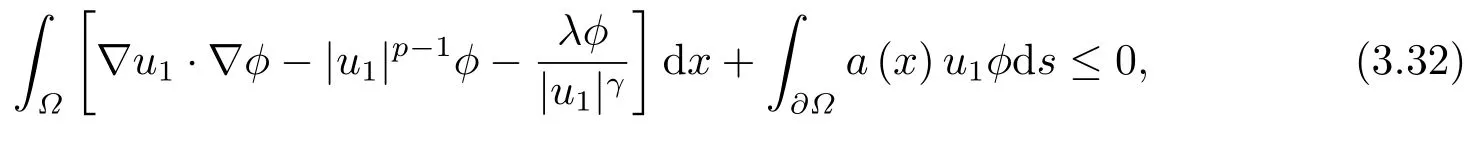


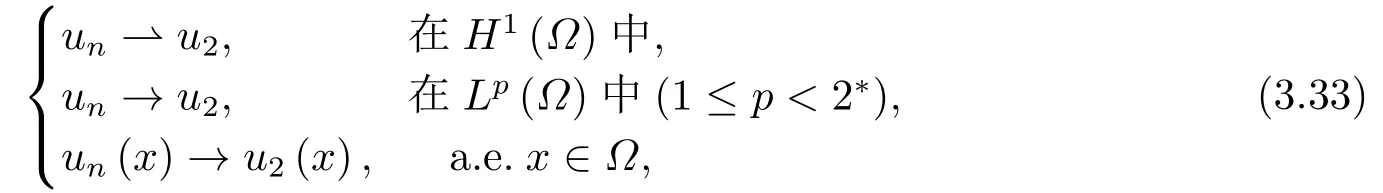
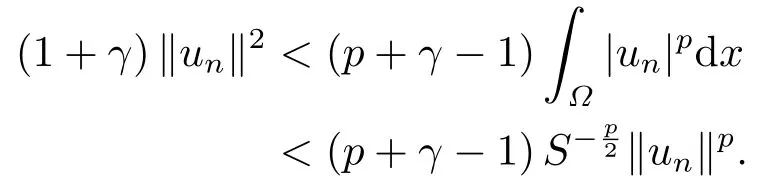

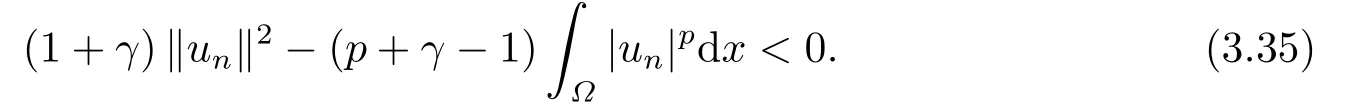


猜你喜欢
杂志排行
应用数学的其它文章
- Atomic Decomposition of Weighted Orlicz-Lorentz Martingale Spaces and Its Applications
- Solvability of Mixed Fractional Periodic Boundary Value Problem with p(t)-Laplacian Operator
- 一类含Hardy-Leray势的分数阶p-Laplacian方程解的单调性和对称性
- 一类非线性趋化方程的能控性及时间最优控制
- Existence of Positive Solutions for a Fractional Differential Equation with Multi-point Boundary Value Problems
- A Higher Order Wolfe Converse Duality in Multiobjective Programming with Cone Constraints
