Atomic Decomposition of Weighted Orlicz-Lorentz Martingale Spaces and Its Applications
2022-01-19ZHANGChuanzhou张传洲LITiantian李甜甜ZHANGXueying张学英
ZHANG Chuanzhou(张传洲), LI Tiantian(李甜甜), ZHANG Xueying(张学英)
(College of Science, Wuhan University of Science and Technology, Wuhan 430065, China)
Abstract: In this paper, we research the atomic decomposition theorems of weighted Orlicz-Lorentz martingale spaces.We give the interpolation theorem of weighted Orlicz-Lorentz martingale spaces and boundedness of matingale’s transform operator on different weighted Orlicz-Lorentz martingale spaces by atomic decompositions.The conclusions develop the theory of Orlicz and Lorentz martingale spaces.
Key words: Atomic decomposition; Interpolation theorem; Martingale’s transform
1.Introduction
Lorentz space was first introduced by Lorentz, which is generalization of Lebesgue spaceLp.In the past, Lorentz spaces have been studied heavily, including the Marcinkiewicz interpolation theorem, Hardy-Littlewood maximal inequality,Apweight, atomic decomposition theorem.The results are widely used not only in harmonic analysis but also in partial differential equations.
Recently, in probability theory, the study of Lorentz martingale spaces has attracted a steadily increasing interest.Weisz[1]introduced the martingale Hardy-Lorentz spaces and discussed the real interpolation between them.JIAO et al.[2−3]studied the weak type inequalities for maximal operator and square operator on Hardy-Lorentz spaces, which improves some results of [1].In 2017, JIAO et al.[4]studied the small-index Hardy-Lorentz martingale spaces and established the predual and John-Nirenberg inequalities for the generalized BMO spaces.They also extended the boundedness of fractional integrals to martingale Hardy-Lorentz spaces.Weisz[5]characterized the dual of multi-parameter martingale Hardy-Lorentz spaces.In [6], HAO and LI studied the atomic decomposition and dual theorem of Orlicz-Lorentz martingale spaces.Inspired by them, we study the weighted Orlicz-Lorentz martingale spaces.
Let (Ω,F,P) be a complete probability space, andFnbe a nondecreasing sequence of sub-σ-algebra ofFsuch thatF=σ(∪nFn),whereFnis generated by countably many atoms.The conditional expectation operators relative toFnare denoted byEn.
LetΦ:[0,∞)→[0,∞) be an increasing function,Φ(0)=0, limt→∞Φ(t)=∞andΦ′be the derivative ofΦ.SetpΦ=andqΦ=It is well known that ifΦis convex then 1≤pΦ ≤qΦ ≤∞and ifΦis concave then 0≤pΦ ≤qΦ ≤1.LetGbe the set of all increasing functionsΦ:[0,∞)→[0,∞) withΦ(0)=0, limt→∞Φ(t)=∞andpΦ >0.
Letωbe a nonnegative random variable on (Ω,F,P).For everyA ∈F, we defineω(A)=∫
A ωdP.For a measurable functionf, we denote its distribution function
λf,ω(t)=ω(x:|f(x)|>t),t ≥0,
and its decreasing rearrangement functionf∗is defined as
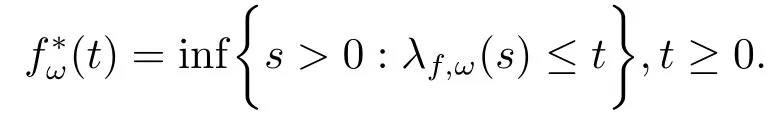
Definition 1.1Given anF-measurable functionfon (Ω,F,P), we define
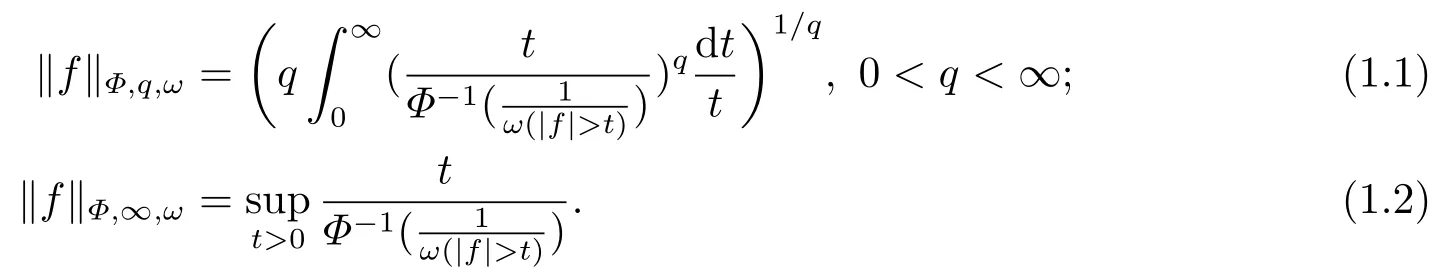
The set of allfwith‖f‖Φ,q,ω < ∞is denoted byLΦ,q,ω(Ω,F,P) (or brieflyLΦ,q,ω) and is called the weighted Orlicz-Lorentz space with indicesΦ,qandω.
These spaces are the generalizations of classical Lorentz spacesLp,qand they coincide withLp,qwhenΦ(t) =tpfor 0< p < ∞andω ≡1.IfΦ(t) =tqfor 0< q < ∞andω ≡1 thenLΦ,q,ωare the usual Lebesgue spacesLq.
Remark 1.1LetΦ ∈G, qΦ−1< ∞andωbe a nonnegative random variable on(Ω,F,P).Then
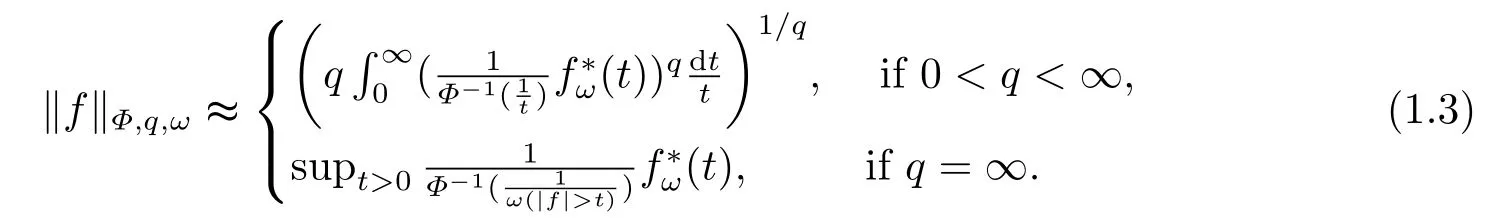
ProofIt’s known that for any measurable functionf, there exists a sequence of nonnegative simple functions{fn}n∈Nsuch thatfn ↑|f|a.e.Moreover,Therefore,it suffices to establish (1.3) for non-negative simple functions by using Lebesgue monotone convergence theorem.
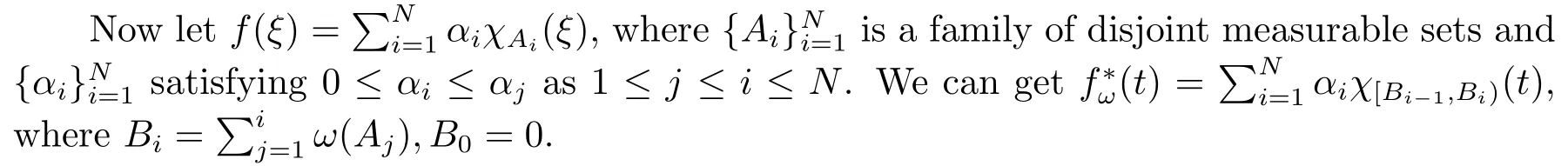
(i) If 0 Similarly, by (1.5) and (1.6) we can get the equivalence as follows: (ii) Ifq=∞,it is easy to get the conclusion. Thus we complete the proof. Remark 1.2LetΦ ∈G,0< s < q, qΦ−1<1/sandωbe a nonnegative random variable on (Ω,F,P).Then It follows from P.64 of [7] that for 0 Remark 1.3(see Proposition 2.6 in [6]) If 0 For a complex valued martingalef= (fn)n≥0relative to (Ω,F,P;(Fn)n≥0), we denote its martingale difference bydfi=fi −fi−1(with conventiondf−1=0) and define the maximal function, the square function and the conditional square function offrespectively as follows: Definition 1.2LetΦ ∈Gandωbe a nonnegative random variable on (Ω,F,P).A measurable functionais called a (1,Φ,∞,ω)-atom (resp.(2,Φ,∞,ω)-atom, (3,Φ,∞,ω)-atom) if there exists a stopping timeτ ∈Tsuch that 1)an=Ena=0,ifτ ≥n; 2)‖σ(a)‖∞(resp.‖S(a)‖∞,‖M(a)‖∞)≤Φ−1 LetΛbe the collection of all sequences(λn)n≥0of nondecreasing,nonnegative and adapted functions, setλ∞= limn→∞λn.Thus the weighted Orlicz-Lorentz martingale spaces are defined as follows: At the end of this section,we make some conventions.Throughout this paper,we denote by the absolute positive constantcthat is independent of the main parameters involved but whose value may differ from line to line.The symbolf ≼gstands for the inequalityf ≤cg.If we writef ≈g, then it stands forf ≼g ≼f. The atomic decomposition is a powerful tool for dealing with some interpolation theorems and fundamental inequalities in martingale theory.In this section,we present and prove one of the remarkable features of martingale function spaces,the atomic decompositions of weighted Orlicz-Lorentz martingale spaces. Theorem 2.1LetΦ ∈G, 0< q < ∞andωbe a nonnegative random variable on(Ω,F,P).If the martingalef=(fn)n≥0is inthen there exists a sequence (ak)k∈Zof(1,Φ,∞,ω) atoms and a sequence (µk)k∈Z∈ℓqof real numbers such that for eachn ≥0 and where the infimum is taken over all the preceding decompositions offof the form (2.1). ProofAssumeLet us consider the stopping times for allk ∈Z, τk=inf{n ∈N:σn+1(f)>2k},inf ∅=∞. For each stopping timeτk, we define=fn∧τk.It is easy to see that Let Ifuk= 0, let= 0 for allk ∈Z,n ∈N.Thenis a martingale for eachk ∈Z.Further we can see and We also get Thus which means that (2.2) is true. It follows thatσ(f −fτM+1)2=σ(f)2−σ(fτM+1)2thenσ(f −fτM+1)≤σ(f),σ(fτN)≤σ(f),andσ(f −fτM+1)→0 andσ(fτN)→0 asM →∞,N →−∞.Then by the Lebesgue convergence theorem, we obtain For the converse part, assume that 0< q ≤1,Φis concave withqΦ−1<1/qand the martingalef=(fn)n≥0has a decomposition of type (2.1).By (1.9), it is easy to see that and Sinceakis a (1,Φ,∞,ω)-atom, then it comes from its definition thatσ(ak) = 0 on the set{τk=∞}.Consequently,{σ(ak)>t}⊆{τk <∞}.Thus we have Thus Taking the preceding decompositions offof the form (2.1), the conclusion holds.This completes the proof of the theorem. Theorem 2.2LetΦ ∈G, 0< q < ∞andωbe a nonnegative random variable on(Ω,F,P).If the martingalef=(fn)n≥0is inQΦ,q,ω, then there exists a sequence (ak)k∈Zof(2,Φ,∞,ω) atoms and a sequence (µk)k∈Z∈ℓqof real numbers such that for eachn ≥0, and Moreover, the sum ∑k∈Zµkakconverges tofinQΦ,q,ωnorm.Conversely, if 0< q ≤1,Φis concave withqΦ−1<1/qand the martingalef=(fn)n≥0has a decomposition of type (2.12),thenf ∈QΦ,q,ωand where the infimum is taken over all the preceding decompositions offof the form (2.12). ProofThe proof is similar to the one of Theorem 2.1, so we only give it in sketch.Iff=(fn)n≥0∈QΦ,q,ω, the stopping timesτkare defined by τk=inf{n ∈N:λn >2k},inf ∅=∞, Thus we get This completes the proof of the theorem. Theorem 2.3LetΦ ∈G, 0< q < ∞andωbe a nonnegative random variable on(Ω,F,P).If the martingalef=(fn)n≥0is inDΦ,q,ω, then there exists a sequence (ak)k∈Zof(3,Φ,∞,ω) atoms and a sequence (µk)k∈Z∈ℓqof real numbers such that for eachn ≥0 and Moreover, the sum ∑k∈Zµkakconverges tofinDΦ,q,ωnorm.Conversely, if 0< q ≤1,Φis concave withqΦ−1<1/qand the martingalef=(fn)n≥0has a decomposition of type (2.16),thenf ∈DΦ,q,ωand where the infimum is taken over all the preceding decompositions offof the form (2.16). ProofThe only difference in the proof is thatλn= ∑k∈Zµk‖S(ak)‖∞χ{τk≤n}is replaced byλn=∑k∈Zµk‖M(ak)‖∞χ{τk≤n}and (ak)k∈Zare of (3,Φ,∞,ω) atoms.We omit the proof. Definition 3.1Φis said to obey the Δ(∇)-condition written often asΦ ∈Δ (Φ ∈∇),if there exists a positive constantc(b>0) such that for arbitraryx,y ≥0.(The details can be seen in [8]) Theorem 3.1LetΦ ∈G ∩Δ∩∇, 0 Moreover by (1.9) we have Then we give the estimation‖σ(T(ak))‖LΦ,∞,ω.SinceTis bounded fromto where{σ(T(ak))>y}=A. Thus Sinceakis a (1,Φ,∞,ν)-atom, it comes from its definition thatσ(ak) = 0 on the set{τk=∞}.Consequently,{σ(ak)>t}⊆{τk <∞}. Thus we have fori=0,1, which means that By Theorem 2.1, we get Thus we complete the proof. Theorem 3.2LetΦ ∈G ∩Δ∩∇, 0 If linear operatorTis bounded fromQΦ,qi,νtoQΦ,∞,ωi, thenTis bounded fromQΦ,q,νtoQΦ,∞,ω, i.e., there exists a constantc>0 such that Now we can only estimateSinceTis bounded fromQΦ,qi,νtoQΦ,∞,ωi, SinceΦ ∈Δ∩∇, similarly to Theorem 3.1 we have where=B. Thus which means that By Theorem 2.2, we get Thus we complete the proof. Similarly, we get the following Theorem 3.3.We omit the proof. Theorem 3.3LetΦ ∈G ∩Δ∩∇, 0 If the linear operatorTis bounded fromDΦ,qi,νtoDΦ,∞,ωi, thenTis bounded fromDΦ,q,νtoDΦ,∞,ω, i.e., there exists a constantc>0 such that The proof is similar to Page 64 in [7] and we omit it. LetΦ ∈G, 0 wherevis adapted process.Then we define the martingale transform as follows: Theorem 4.1LetΦ ∈G ∩Δ∩∇, 0< q0,q1<1, 0< r1,r2≤∞,ωis nonnegative random variable and Thus by the interpolation theorem we have Thus we complete the proof. Similarly, we get the following theorems. Theorem 4.2LetΦ ∈G ∩Δ∩∇, 0< q0,q1<1, 0< r1,r2≤∞,ωis nonnegative random variable and Ifv ∈V,thenTvis bounded fromQΦ(r2),q,ωtoQΦ(r),∞,ω, i.e., there exists a constantc >0 such that Theorem 4.3LetΦ ∈G ∩Δ∩∇, 0 Ifv ∈V,thenTvis bounded fromDΦ(r2),q,ωtoDΦ(r),∞,ω, i.e., there exists a constantc >0 such that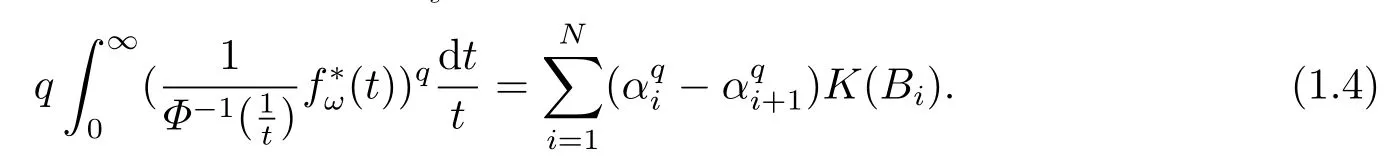
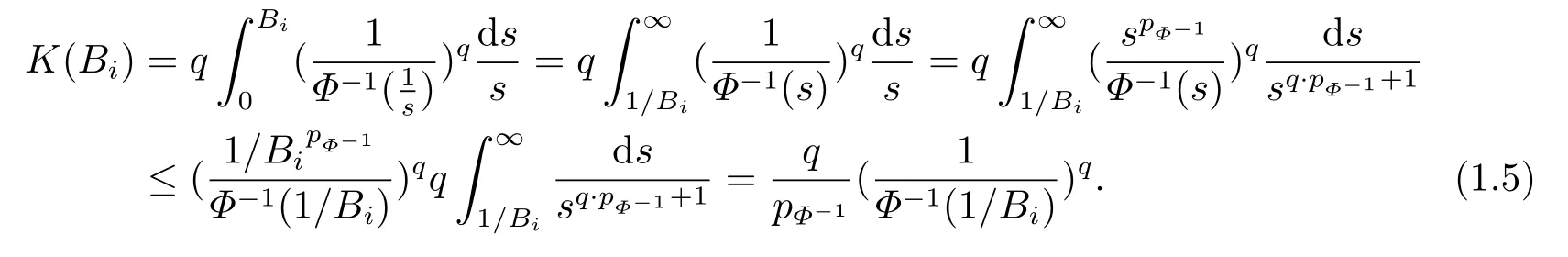
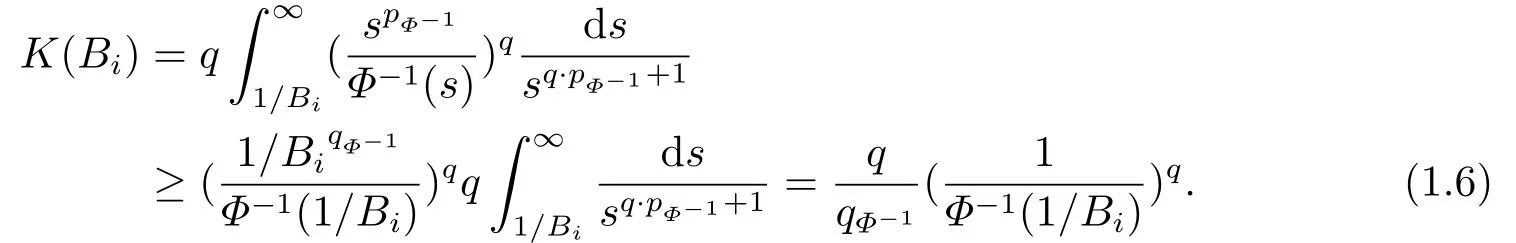
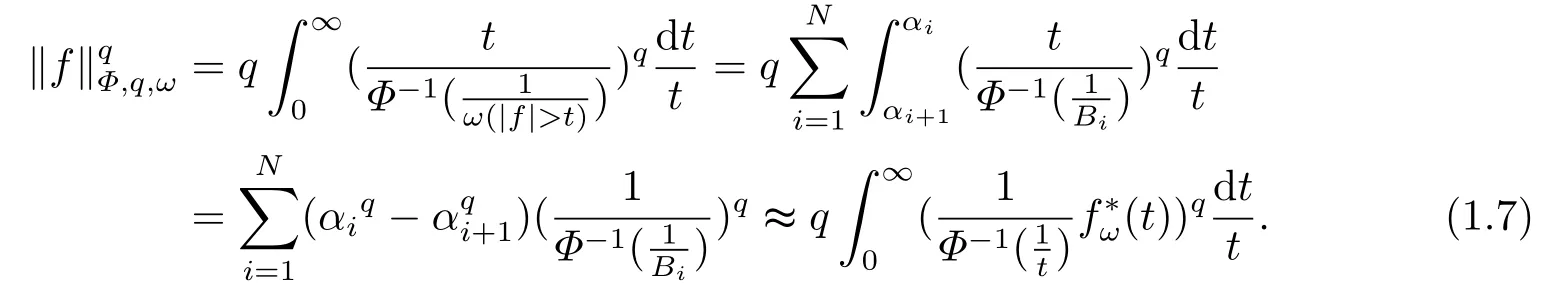

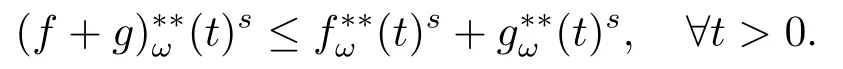
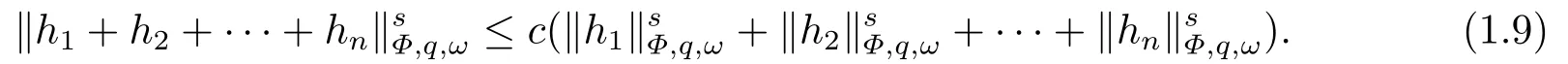
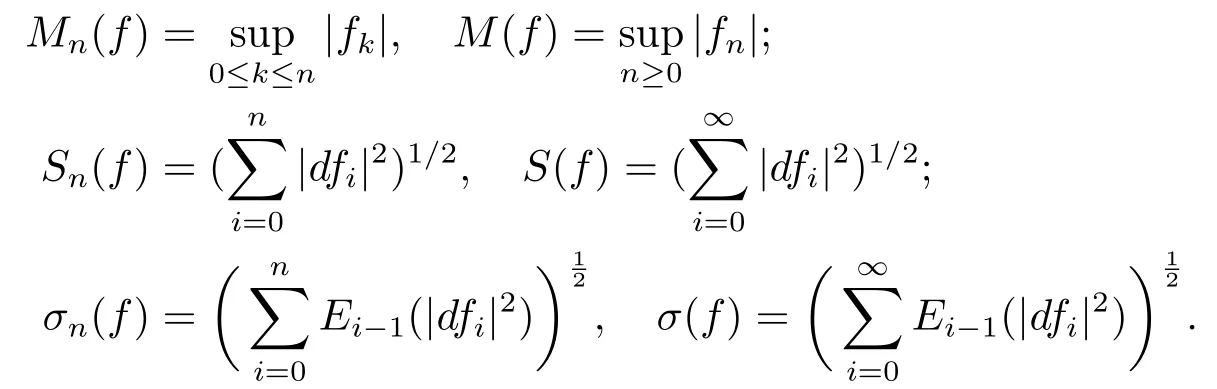
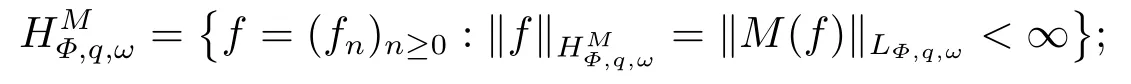
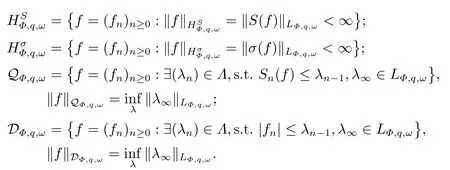
2.Atomic Decomposition of Weighted Orlicz-Lorentz Martingale Spaces


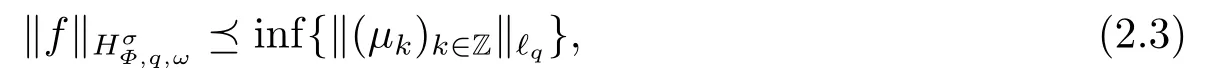
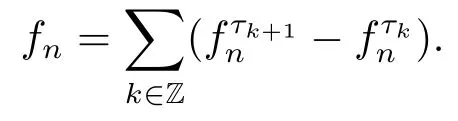
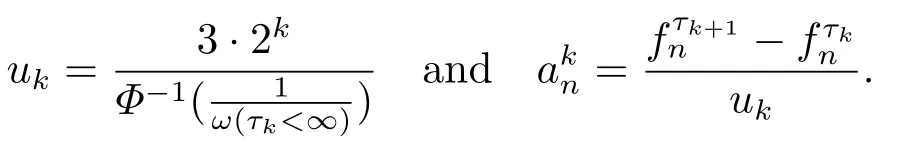

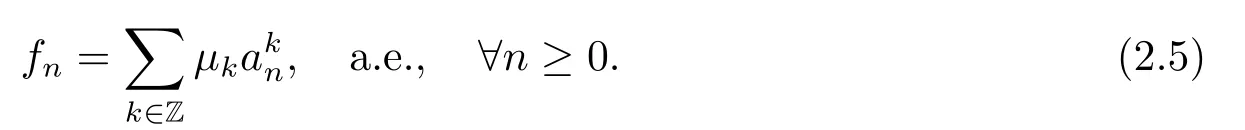
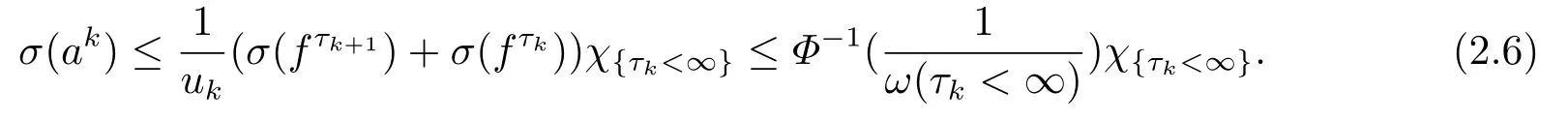
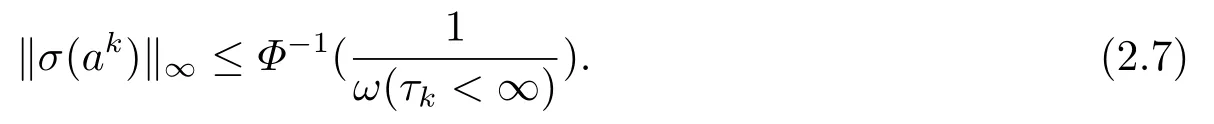
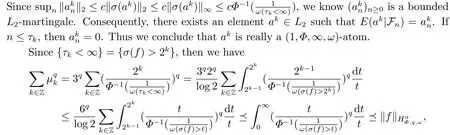
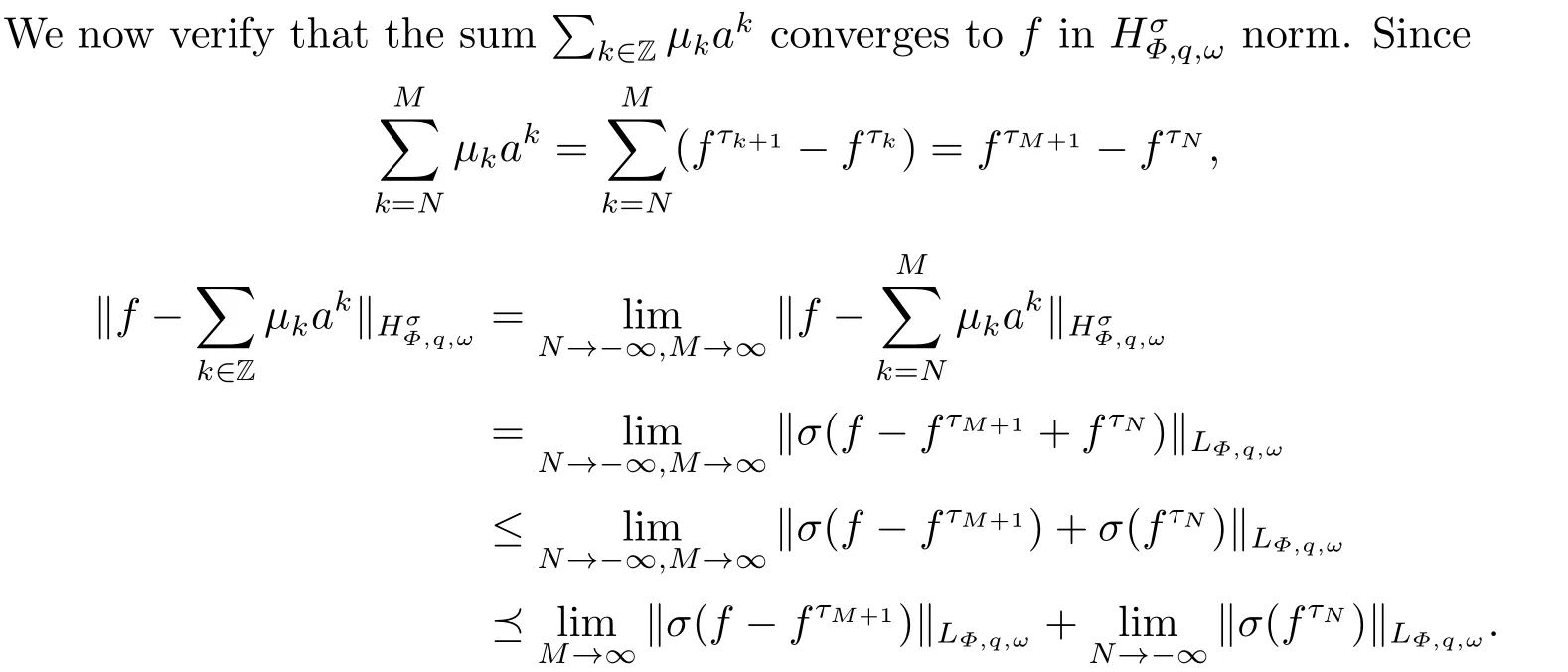
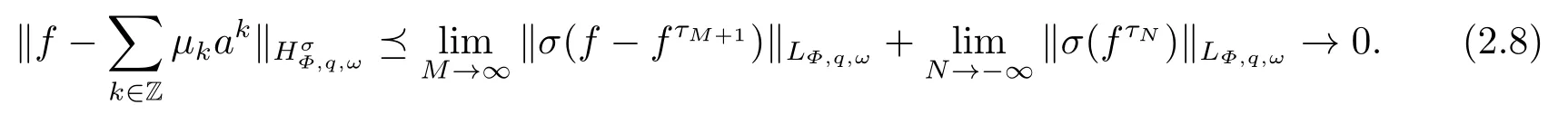

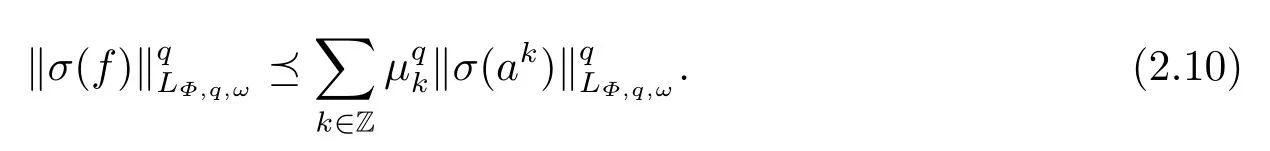
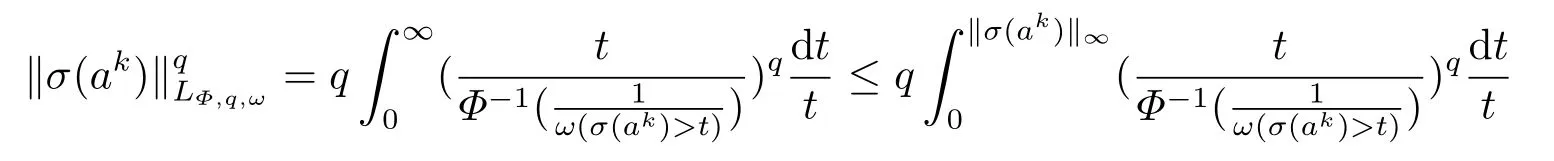
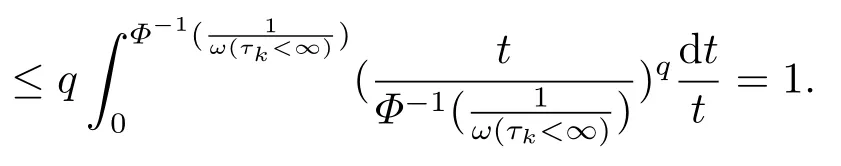
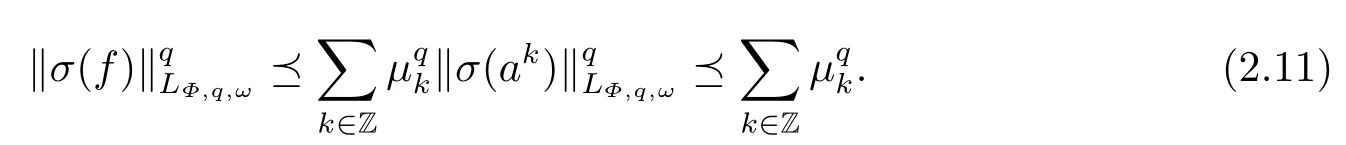


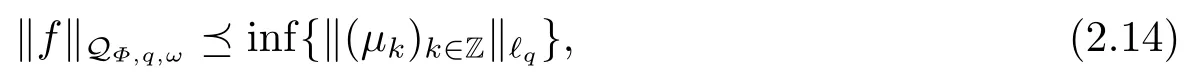

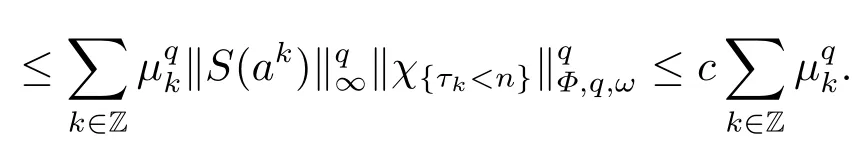
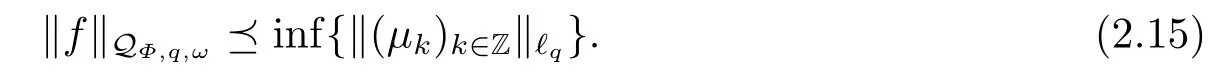


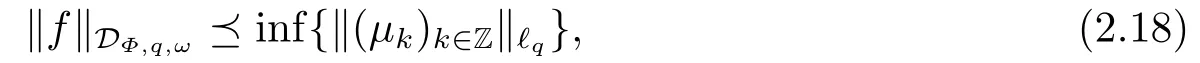
3.Interpolation of Weighted Orlicz-Lorentz Martingale Spaces


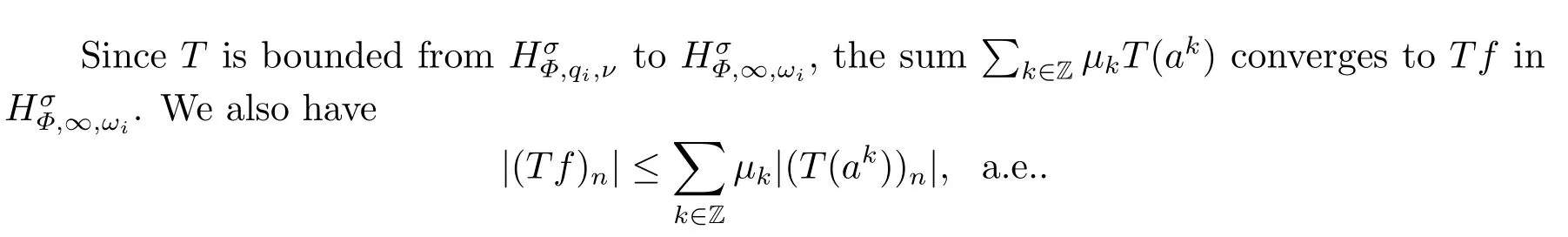
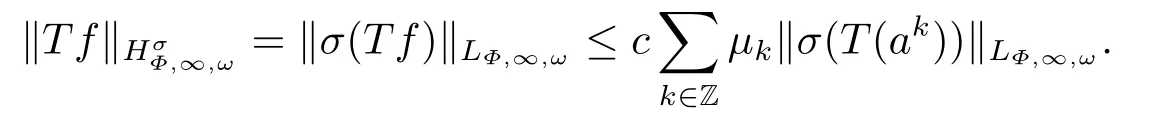


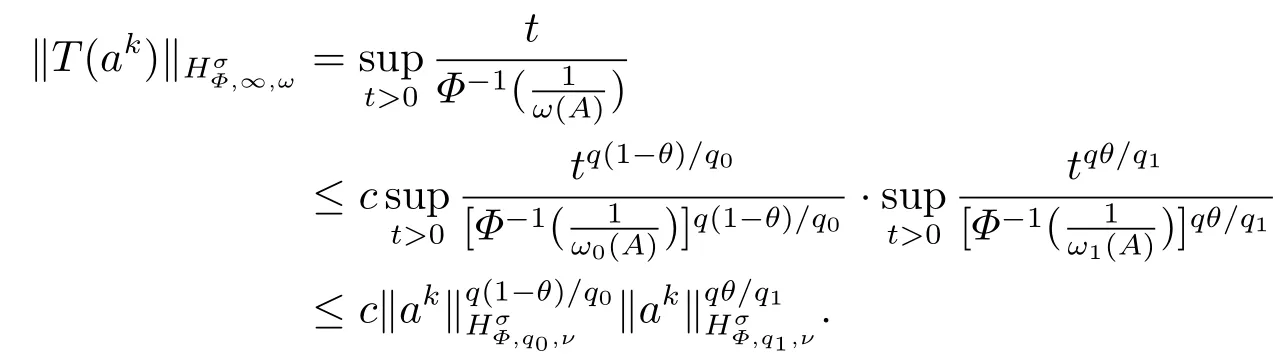
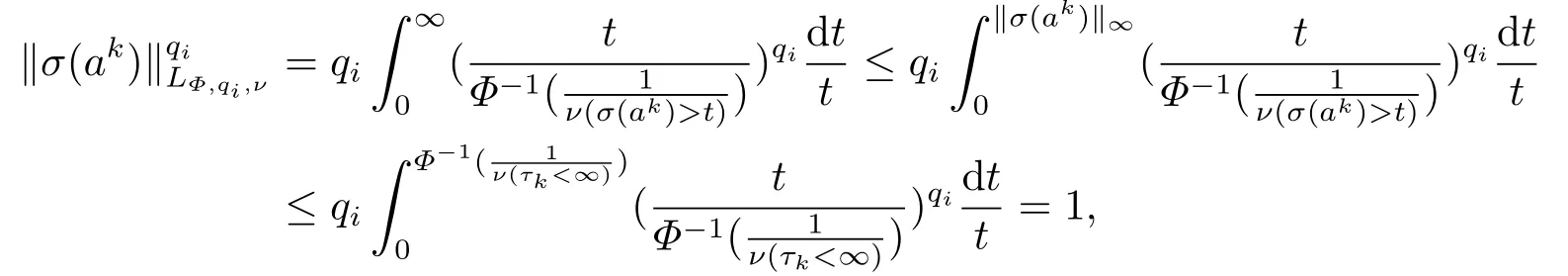
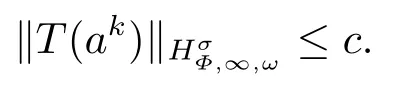

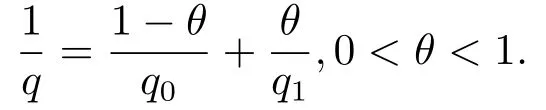
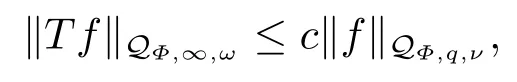

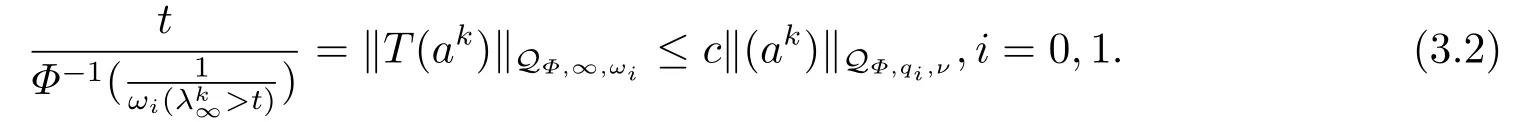
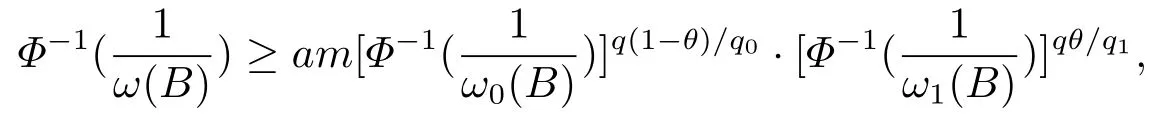
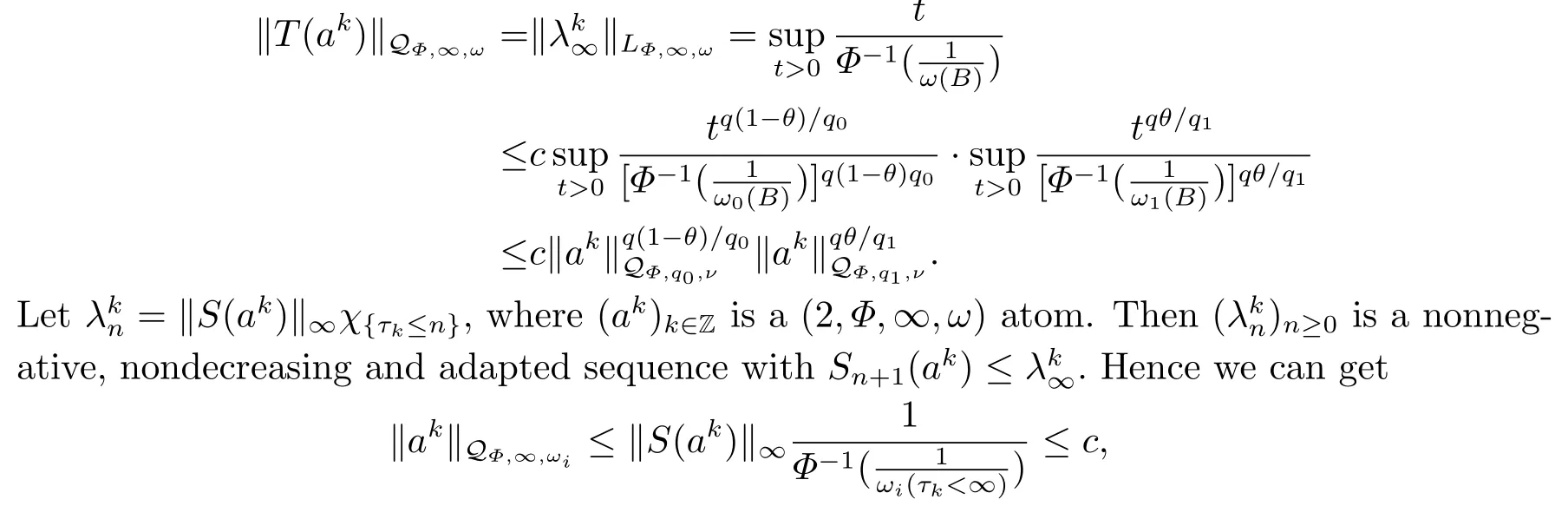
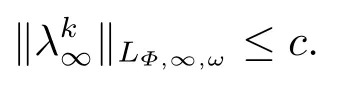
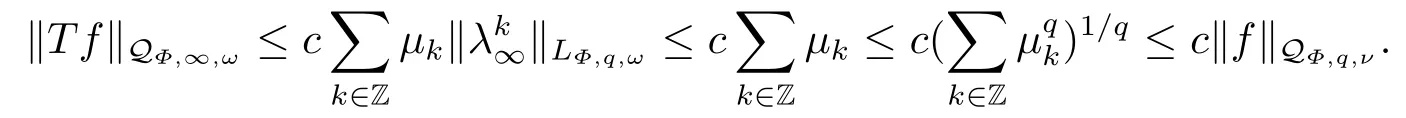
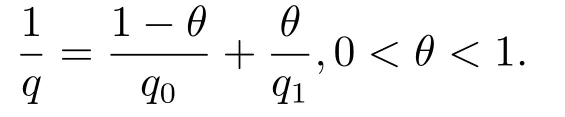
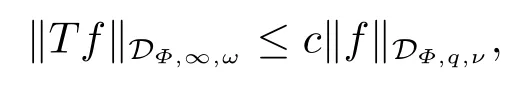
4.Boundedness of Martingale’s Transform Operator
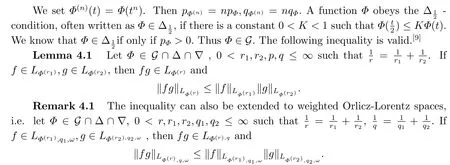
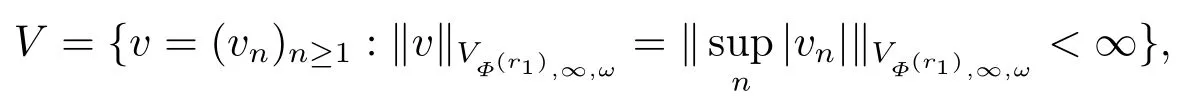
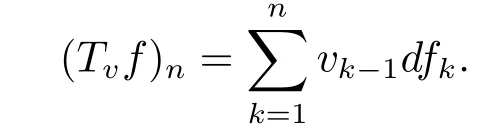
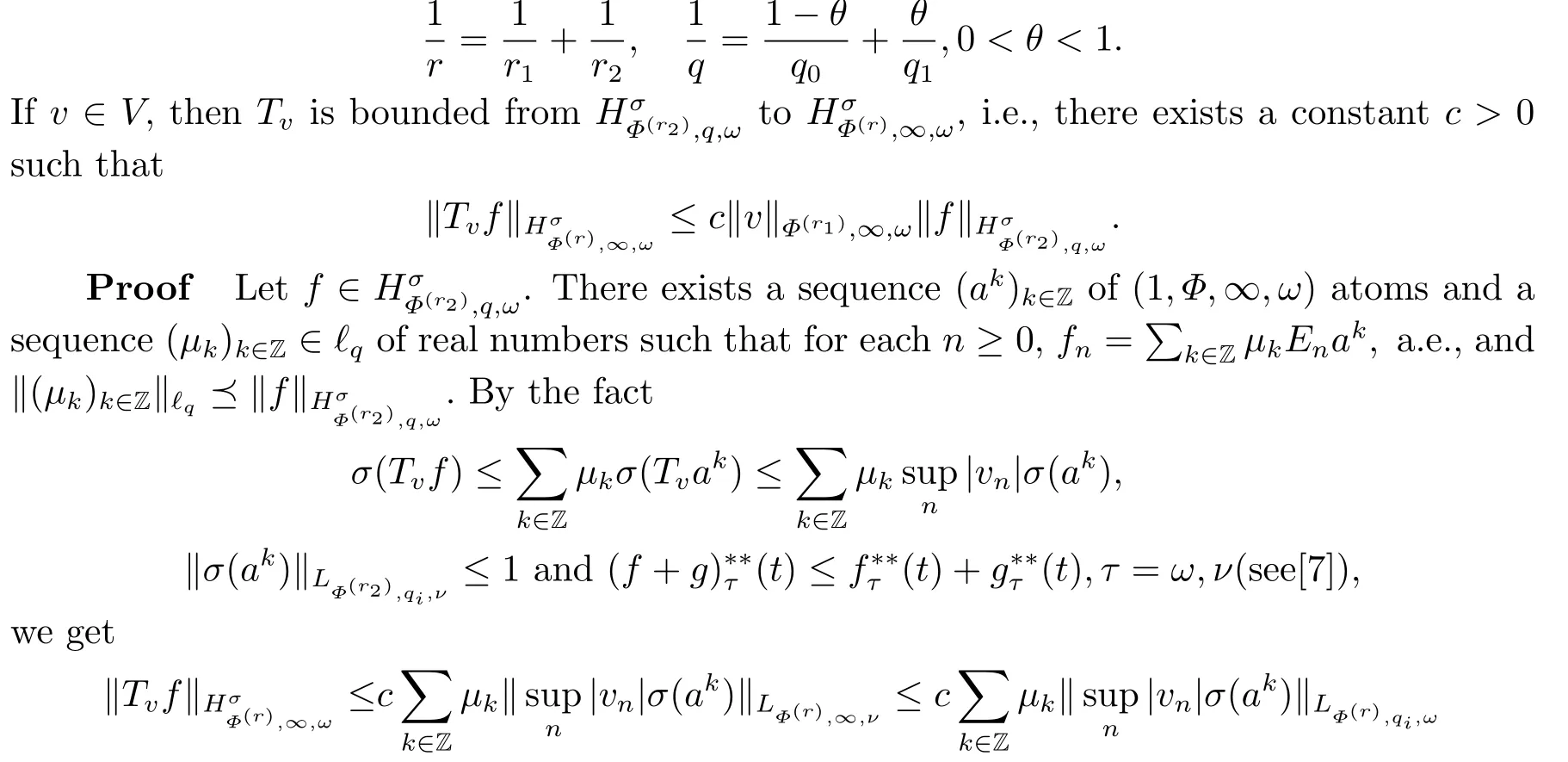
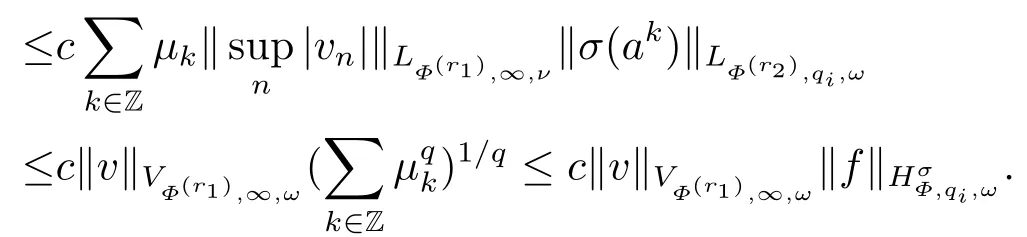
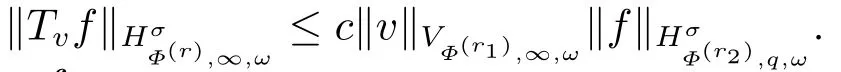
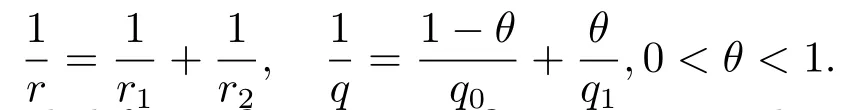

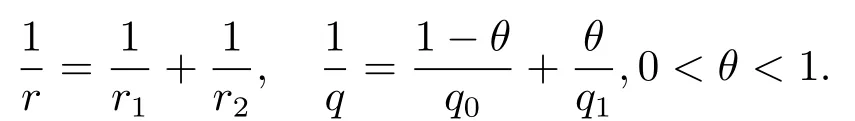
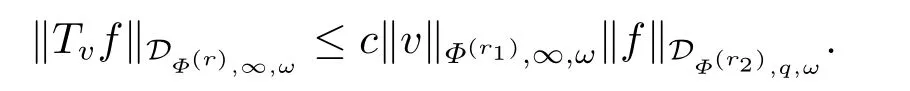
杂志排行
应用数学的其它文章
- Solvability of Mixed Fractional Periodic Boundary Value Problem with p(t)-Laplacian Operator
- 一类含Hardy-Leray势的分数阶p-Laplacian方程解的单调性和对称性
- 一类非线性趋化方程的能控性及时间最优控制
- Existence of Positive Solutions for a Fractional Differential Equation with Multi-point Boundary Value Problems
- 奇异椭圆方程Robin问题多重正解的存在性
- A Higher Order Wolfe Converse Duality in Multiobjective Programming with Cone Constraints
