一类非线性趋化方程的能控性及时间最优控制
2022-01-19李文娟张亮
李文娟, 张亮
(武汉理工大学理学院, 湖北 武汉 430070)
1.引言
设Ω ⊂R3为带光滑边界∂Ω的有界邻域,ω为Ω的非空开子集.令T >0, 记QT=Ω ×(0,T),ΣT=∂Ω×(0,T), Lebesgue空间Lp(Ω),Lp(QT)(1≤p ≤∞)的范数分别为|·|p,‖·‖p.
考虑如下非线性趋化方程

其中ut=∂u/∂t,vt=∂v/∂t.∂ν=∂/∂ν表示边界∂Ω的外法向量.1ω指ω上的特征函数,g=g(x,t)为控制函数,u=u(x,t)为细菌密度,v=v(x,t)为氧气浓度,χ >0为给定的常数,u0(x)和v0(x) 表示初始值, 函数f(v)为氧气消耗速率.为简化符号, 本文省略函数表达式中的x和t.这里f和χ满足

且

定义1.1称函数(u,v)为方程(1.1)的弱解, 如果
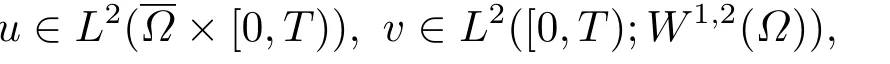
u ≥0,v ≥0, a.e.在Ω×(0,T)中, 且
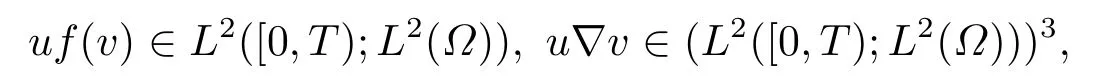
并且等式

方程(1.1)是由Tuval和Cisneros等[15]提出的, 该方程主要是为了描述在氧气的趋化作用下细菌向液体与空气接触面的游动和在细菌重力的作用下液体产生流动这一生物过程.本文将讨论非线性趋化方程(1.1)的能控性及时间最优控制的存在性.
当方程(1.1)没有控制项时, 该方程为标准的趋化模型, 也是一类典型的非线性Keller-Segel方程, 即

关于Keller-Segel方程(1.4)的研究, 在过去的几年里取得了一些进展.若f是连续可微的单调递增函数且满足f(0) = 0, 在有界区域Ω ⊂RN(N= 2,3)上, Lorz[16]得出了局部弱解,当N=3且参数χ和f满足条件(1.2)和(1.3)时, Winkler[18]给出在带光滑边界的有界凸区域上方程(1.1)弱解的存在性.


然而, 关于Keller-Segel方程在控制方面的相关成果很少.在文[7]中作者研究了Keller-Segel方程的最优控制问题.在文[9]中, 作者给出如下描述药物浓度不瞬时溶解情况下Keller-Segel方程的局部精确能控性,
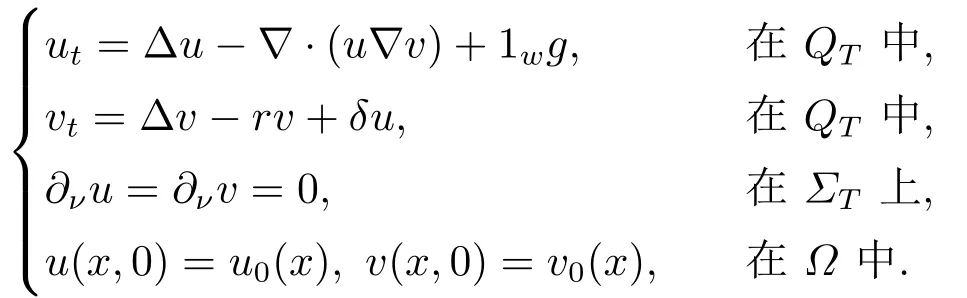
本文考虑方程(1.1)的能控性和时间最优控制, 原因如下: 其一, 由于drift-diffusion 项的存在, 使得在证明方程(1.1)的正则性和线性方程的能观性估计等方面更为困难; 其二, 非线性项uf(v)的存在使得方程(1.1)的难度更大, 但结果也更为丰富; 其三, 本文考虑的是方程组在一个控制下的能控性问题和时间最优控制问题, 该类问题近年来愈发引起关注.
本文将采用近年来发展的处理非线性方程的经典方法证明(1.1)的能控性: 首先将非线性方程线性化, 然后运用线性方程的能控性结果, 结合不动点定理, 最后得到非线性方程的能控性.
2.线性抛物方程的正则性
考虑如下的线性抛物型方程组

其中a1(·,·),a2(·,·),B2(·,·)∈L∞(QT), B1(·,·)∈L∞(QT)N, B1·ν=0在ΣT上.ρ0(·), θ0(·)∈L2(Ω), G ∈L2(QT).
命题2.1设a1,a2,B2∈L∞(QT),B1∈L∞(QT)N,B1·ν=0在ΣT上.
1) 若ρ0, θ0∈L2(Ω),G ∈L2(QT), 则方程(2.1)有唯一解(ρ,θ)∈L2([0,T))×L2([0,T);W1,2(Ω)), 且满足
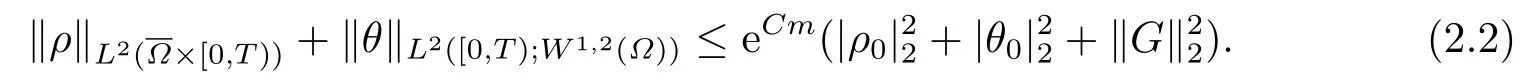
2) 当2≤p < ∞时, 若G ∈Lp(QT),ρ0∈Lp(Ω), θ0∂νθ0= 0在∂Ω上,则方程(2.1)有唯一解(ρ,θ)∈Lp(QT)×且满足
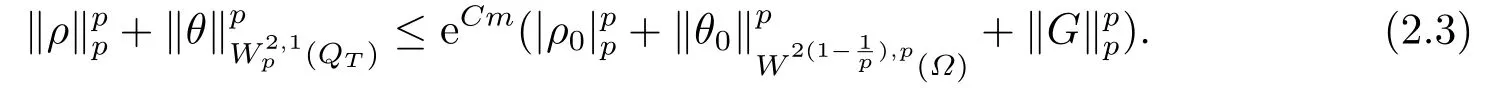
3) 当p >5时, 若G ∈L∞(QT),ρ0∈L∞(Ω), θ0∈W1,p(Ω), ∂νθ0= 0在∂Ω上, 则方程(2.1)有唯一解(ρ,θ)∈L∞(QT)×L∞(QT), 且满足

其中

并且常数C=C(Ω).
证由于解的存在性证明类似于文[1], 不等式(2.2)与(2.3)的证明相似, 故本文只证明不等式(2.3)和(2.4)成立.
首先, 证明不等式(2.3)成立.
对(2.1)的第一、二个方程分别乘|ρ|p−2ρ, |θ|p−2θ, 并分别在Ω上积分, 可得

对关于t微分, 并利用(2.1)的第二个方程, 有
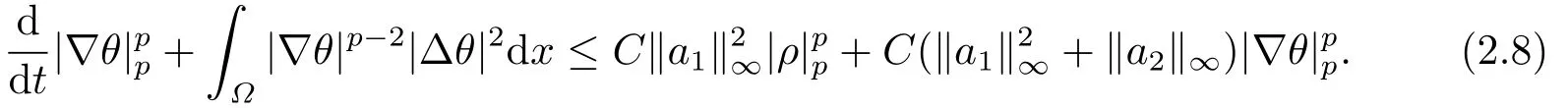
对(2.1)的第二个方程利用最大正则性[9]得
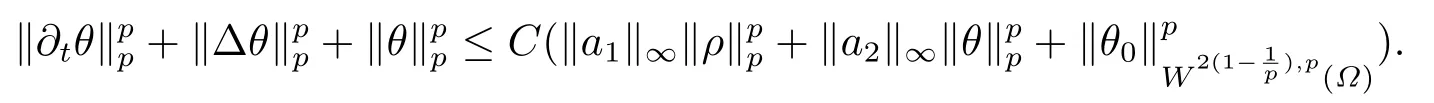
对(2.6)-(2.8)利用Gronwall不等式, 并在[0,T]上积分, 可得

综上可得

故不等式(2.3)成立.
然后证明不等式(2.4)成立.
对于p ∈(1,∞),A=:Ap指扇形算子
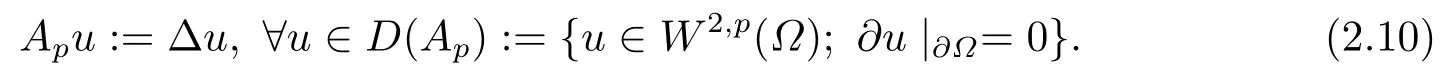
假设γ为正常数,ρ0∈C(().{e−tA}t≥0和{e−t(A+γ)}t≥0是由Lp(Ω)(1< p <∞) 中−A和−(A+γ)生成的解析C0半群.关于(2.1)第一个方程的解可表示为

对上式(2.11)两边取范数可得
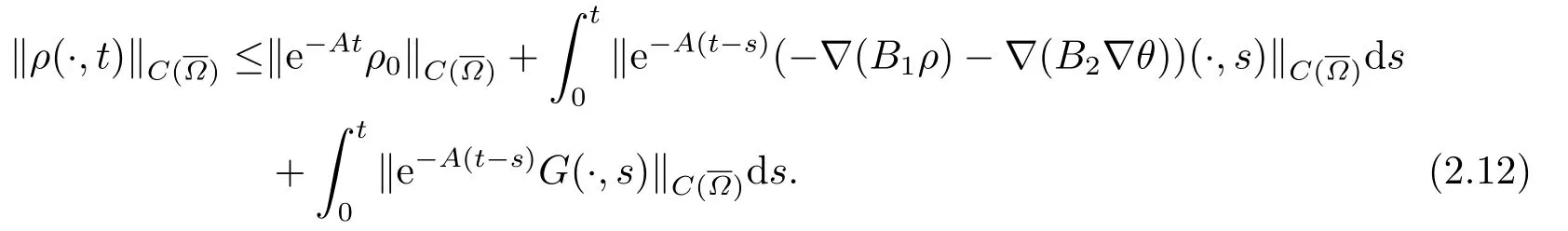
对于任意的0≤s 设τ >0, D((A+γ)τ)是具有图像范数的Banach空间, 并满足如下嵌入性质 由于p >5, 取ε足够小,τ满足(2.15), 对(2.12)通过Hlder不等式和文[9]中的Proposition 1得 由(2.9), (2.12)-(2.16)得 同理关于(2.1)第二个方程的解可表示为 对式(2.18)两边取W1,p(Ω)范数 对(2.19)作估计 再通过(2.9)、(2.19)-(2.21)和Sobolev嵌入W1,p(Ω)(p>3), 有 引理3.1设z(x,t)为方程 的弱解,fi ∈L2(QT), ∂fi/∂xi是fi的弱导数(i= 1,...,N), 存在常数C=C(Ω,ω0,d)和常数λ0=λ0(Ω,ω0,d)>1, 对所有的λ ≥λ0和s ≥r(λ)(T+T2), 有 其中d是实数, 且 不等式(3.2)的证明类似于文[6], 证明过程只需将ω=esνu替换成ω=(sφ)desνu, 并利用相同的方法估计. 考虑线性方程组(2.1)的共轭方程组 其中ζT,ϱT ∈L2(Ω).已知线性抛物方程的精确能控等价于其共轭方程的能观性估计, 因此,为了研究方程(2.1)的零可控, 需对共轭方程(3.4)进行能观性估计, 为了得到共轭方程的能观性估计, 需利用共轭方程的Carleman估计. 其中常数C1=C1(Ω, ω, ω0), 且 证存在常数C0(Ω,ω0) 和满足 对所有的和s ≥r(λ)(T+T2), 对(3.4)运用引理3.1, 并分别令d=2, d=0, 有 其中(ζ,ϱ)为方程(3.4)关于ζT,ϱT ∈L2(Ω)的解,Ci(i=1,2,3)为仅依赖于Ω,ω,ω0的正常数. 需对不等式(3.9)的后半部分作处理. 令(Ω),ξ=1在ω0上;ξ=0在中; 0≤ξ ≤1在ω中, 并且满足 令η=λ4(sφ)3e2sν,将(3.4)的第一个方程化为a1ϱ=∂tζ+Δζ+B1∇ζ, 再两边同乘ϱηξ, 可得 上式利用分部积分得 通过(3.3)和(3.10)得 对Ψ1,Ψ2利用Cauchy不等式, 有 其中ε1和ε2是任意的正常数. 再利用Cauchy不等式得 (3.5)成立.证明完毕. 众所周知, 方程(2.1)关于L2(QT)的零可控等价于方程(3.4)的可观测不等式, 其中(ζ,ϱ)为方程(3.4)的解.为了使控制在空间L∞(QT)上, 需建立改进的可观测不等式. 命题3.3存在正常数λ和s, 对任意的T >0, ζT,ϱT ∈L2(Ω), 则方程(3.4)的解(ζ,ϱ)满足 这里m由(2.5)给定. 证存在正常数λ1=λ1(Ω,ω,ω0), 对于任意的λ ≥λ1和s ≥r(λ)(T+T2), 令 根据引理3.2, 对方程(3.4)利用分部积分, 可得 由(3.6), (3.7)得 由于 再利用(3.5), 可得 故得到(3.14)成立. 证明非线性方程(1.1)的局部精确能控: 先证明线性方程(2.1)的零可控, 再利用不动点定理. Ⅰ 在一个控制下线性方程的零能控性 定理4.1对于T >0, 任意的(ρ0,θ0)∈L2(Ω)×L2(Ω), 存在控制函数g ∈L∞(QT),使得方程(2.1)相对于g的解(ρ,θ)满足(ρ,θ)∈L2([0,T))×L2([0,T);W1,2(Ω)),ρ(x,T) =θ(x,T)=0,∀x ∈Ω, 且控制函数g满足 其中C为依赖于Ω,ω的正常数,m满足(2.5). 证对于∀ε>0, 考虑下面的最优控制问题 其中 这里(ρ,θ)是方程(2.1)相对于g的解.存在控制问题(4.2)的最优对(gε,(ρε,θε)),通过Pontryagin最大原理, 可得 令ν0=则有 其中r(λ)由(3.3)给定. 假设参数λ,s足够大, 使得可观测不等式(3.14)和 成立. 对每个i(i=0,1,...,k,k+1), 定义 对方程(4.7)利用Lp −Lq估计, 则方程的解可表示为 对(4.8), (4.9)利用Lpi−1−Lpi估计, Young卷积不等式和文[9]中的Proposition 1, 可得 又 通过(4.10)-(4.12)得‖^ζi‖pi+‖^ϱi‖pi ≤eCm(‖^ζi−1‖pi−1+‖^ϱi−1‖pi−1),上式从0到k迭代, 再利用(4.4), 则有 即 由(4.11)得 再由(4.12)和(4.13)可得 利用嵌入不等式, 有 即 选择δ足够小, 由r(λ)>4, 可得通过(4.5), (4.14)得 Ⅱ 非线性方程的局部精确能控性 这部分, 通过线性抛物方程(2.1)的局部精确零能控性和Kakutani不动点定理来证明非线性方程(1.1)的局部精确能控性. 定理4.2p >5, (是方程(1.4)相对于的轨迹, 存在不依赖于T的正常数C, 对于任意的(当满足 证首先将非线性抛物方程(1.1)线性化. 其中(ρ,θ)是方程(4.17)的轨迹. 令K={(α,β)∈L∞(QT)×L∞(QT)| ‖α‖∞≤e−ςTm0,‖β‖∞≤m0}, 这里m0>0.对任意的(α,β)∈K, 将(4.17)化为线性方程, 有 故方程(1.1)的局部精确可控等价于方程(4.18)的局部零可控.已知(ρ,θ)是方程(4.18)相对于g和(α,β)的解, 由定理4.1得ρ(x,T)=θ(x,T)=0, 且控制函数满足以下估计 然后利用Kakutani不动点定理. 对于(α,β)∈K, 定义一个多值映射Λ:K →2L2(QT),(α,β)→Λ(α,β), Λ(α,β)={(ρ,θ)∈L2(QT)×L2(QT);∃g满足(4.19),方程(4.18) 相对于 (α,β) 和g的解(ρ,θ),满足ρ(x,T)=θ(x,T)=0 a.e.在Ω中}. 下面将证明多值映射Λ满足Kakutani不动点定理. 1) 证明Λ(α,β)是(L2(QT))2的非空紧凸集.通过前面的讨论, 可得Λ(α,β)对每个(α,β)∈K是非空凸的, 通过(4.19)和(2.4)得(ρ,θ)满足 通过(4.20)可得,Λ(α,β)在L2(Ω×[0,T))×L2([0,T);W1,2(Ω))中对每个(α,β)∈K是有界的, 再通过Aubin-Lions引理得Λ(α,β)是(L2(QT))2的紧子集. 2)证明Λ是上半连续.取K中的有序数列(αn,βn)在L2(QT)中强收敛于(α,β),对每个n.设(ρn,θn)∈Λ(αn,βn), 由Λ(αn,βn)的定义, 对每个n, 存在gn, 使得(ρn,θn)为以下方程的解, 并且ρn(x,T)=θn(x,T)=0, 对几乎所有的x ∈Ω, 此外, 控制函数gn满足 由(4.22)和命题2.1 得 在方程(4.21)中, 当n →∞时, 可得(4.21)相对于(α,β)的弱解为(ρ,θ).下面需证明(ρ,θ)∈Λ(α,β).令Yn=ρn −ρ,Zn=θn −θ,Gn=1wgn.设(Yn,Zn)为以下方程的解 其中‖(B2)αn‖∞≤C,‖(a1)βn‖∞≤C,‖(a2)βn‖∞≤C, 对所有的n成立.通过能量估计, 有 又(ρ,θ)是(4.18)的解.当2≤p<∞时, 由命题2.1(ii)得 由(4.19)得1wg是有界的, 通过Sobolev嵌入(QT)1(QT) (P >5), 可得 因为(αn,βn)→(α,β)在L2(QT)中强收敛, (Yn,Zn)→(0,0)在L2(QT)中强收敛, (Gn −G)→0在L2(QT)中弱收敛, 当n →∞时, (4.25)的右边趋于0, 所以|Yn(·,t)|2→0,|Zn(·,t)|2→0,∀t ∈[0,T], 由于ρn(x,T) =θn(x,T) = 0,∀x ∈Ω, 可得ρ(x,T) =θ(x,T) = 0,∀x ∈Ω,即(ρ,θ)∈Λ(α,β).综上可得,Λ是上半连续. 本节, 利用定理4.2的局部精确能控性, 讨论具有控制的非线性趋化方程(1.1)关于时间最优控制的存在性问题. 则(1.5)至少存在一个时间最优控制. 取T >T1, 作辅助函数


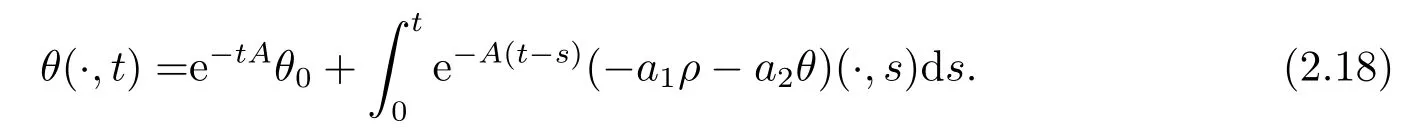


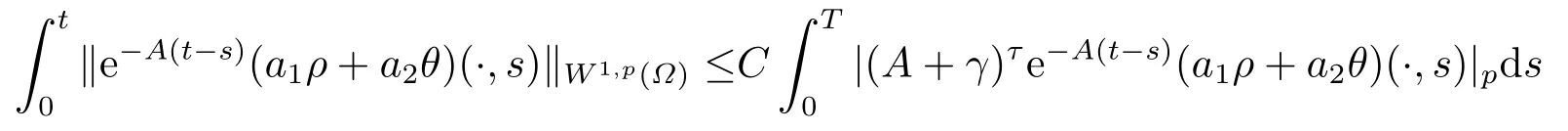
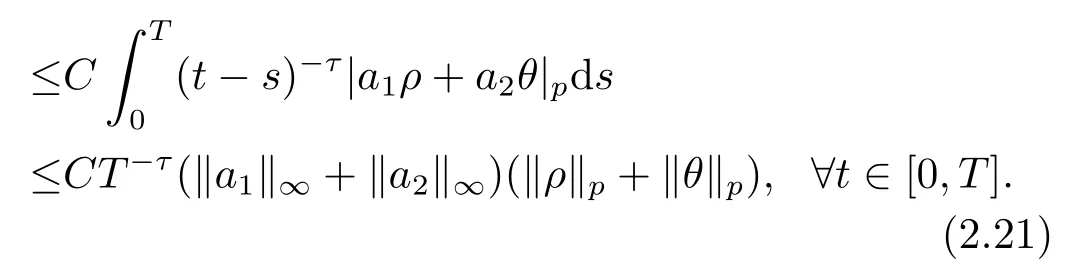


3.能观性估计

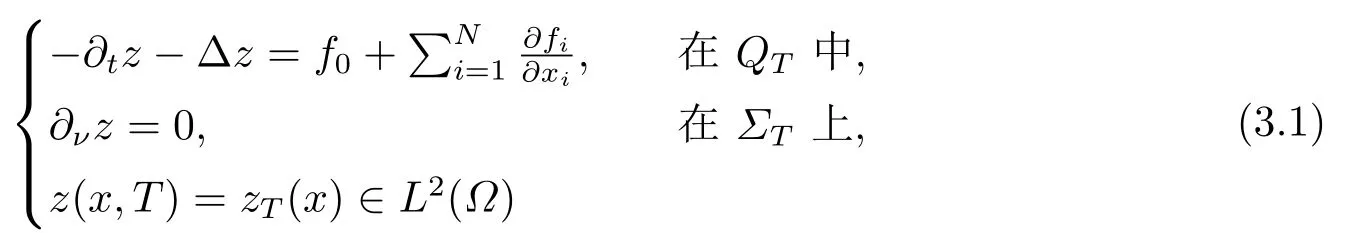

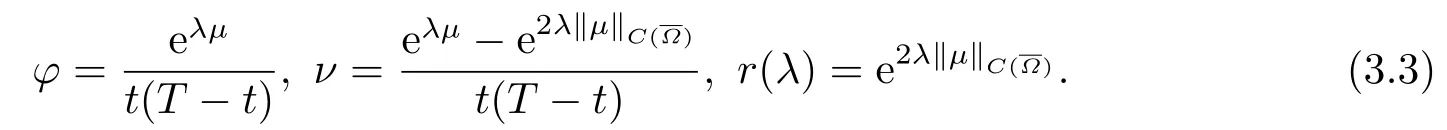


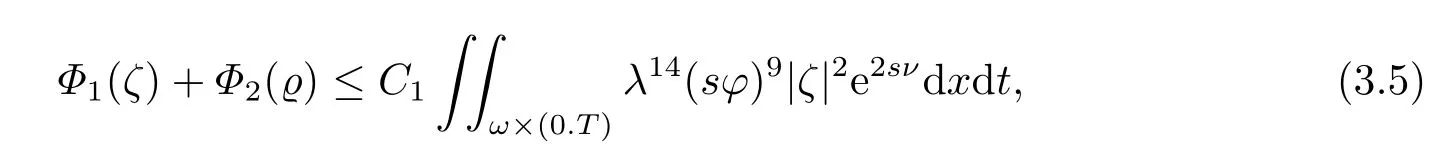
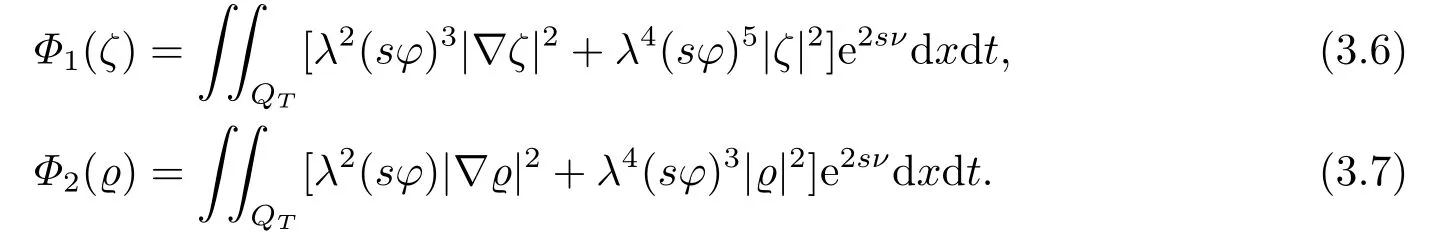

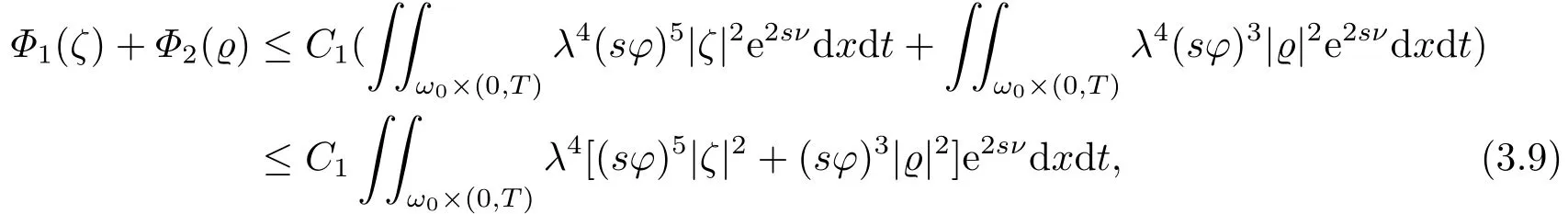
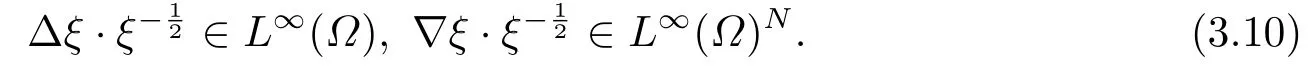




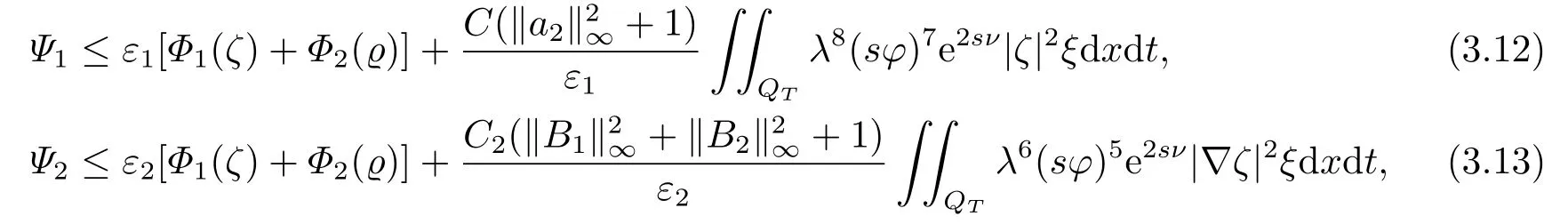
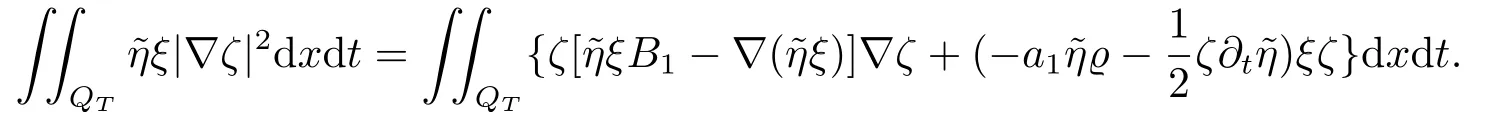
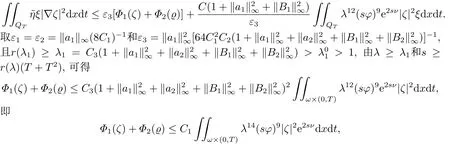
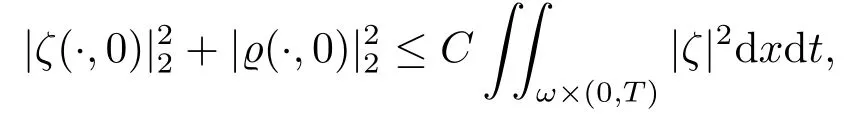
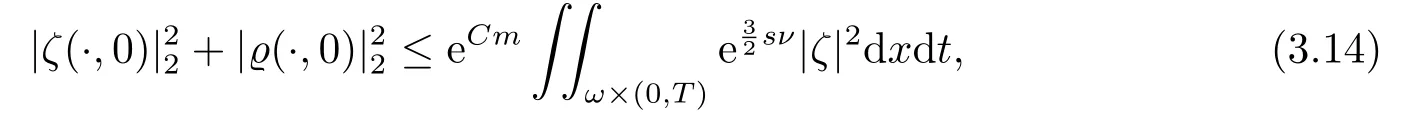
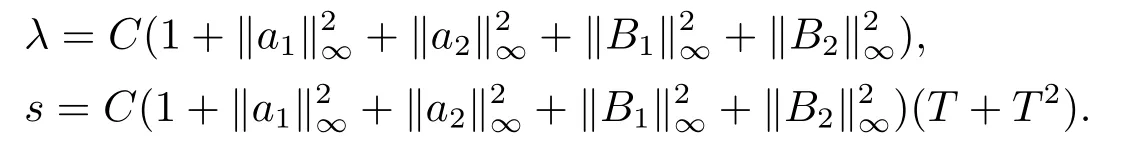
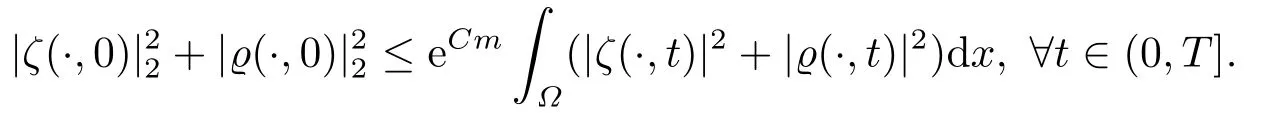
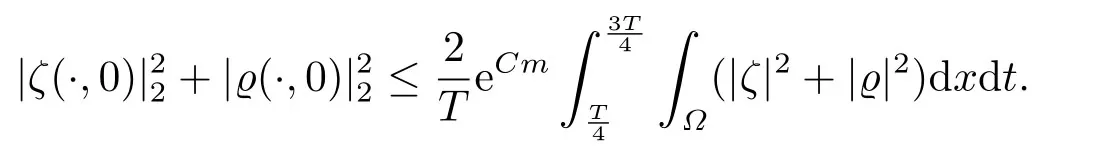

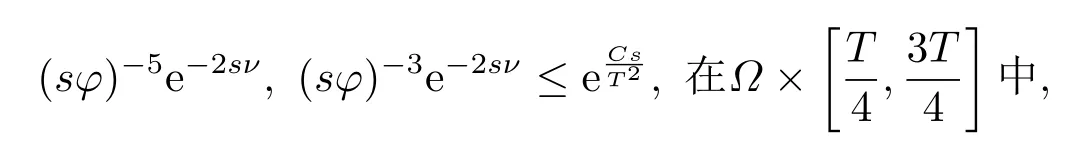

4.能控性


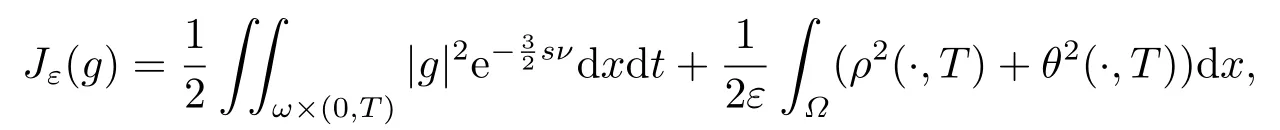


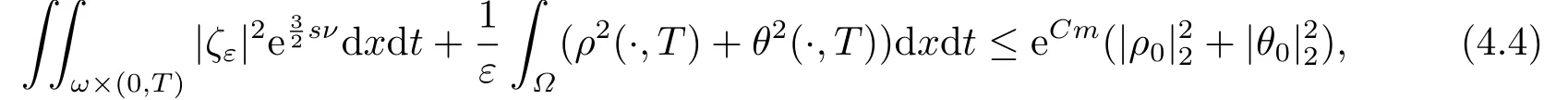



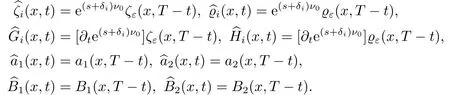
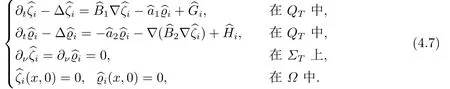
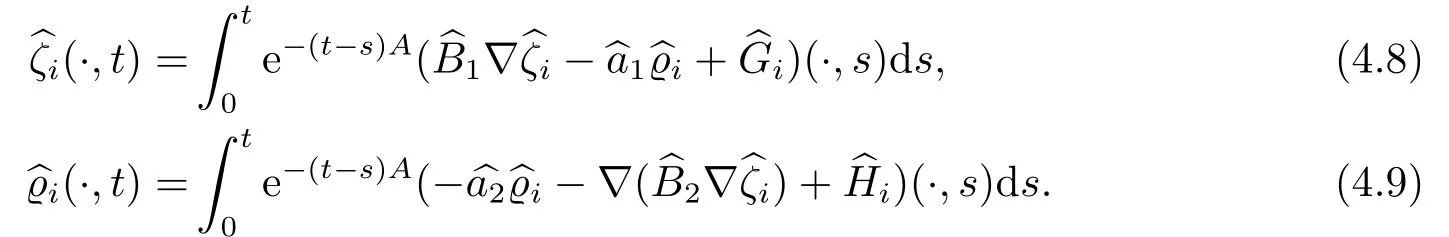
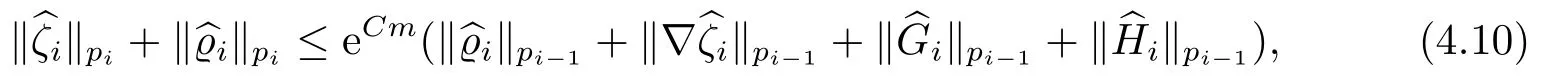

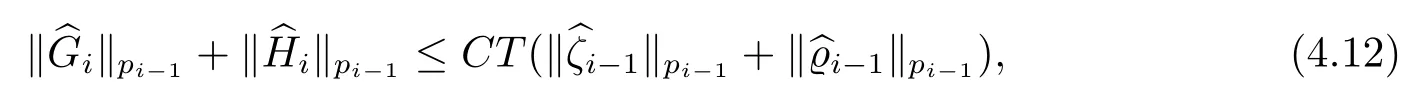
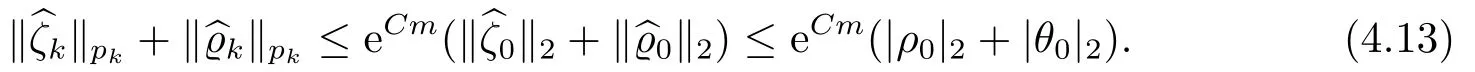
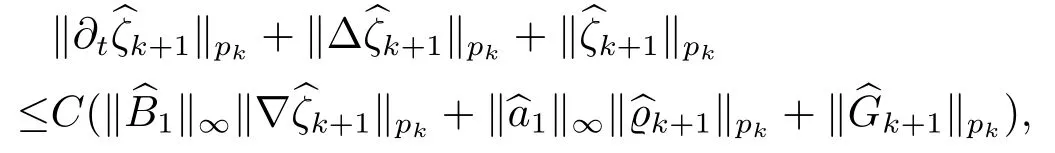

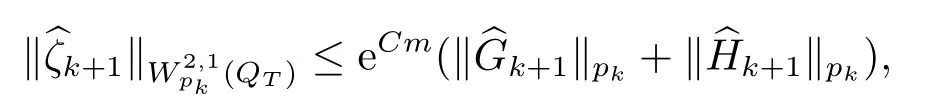

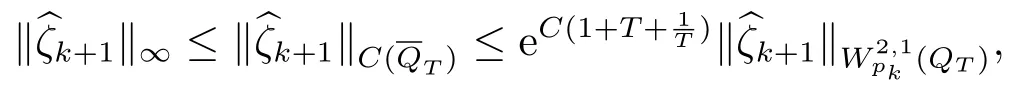

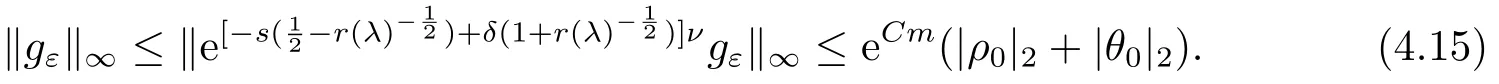






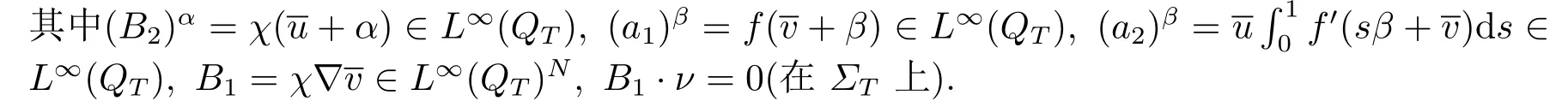
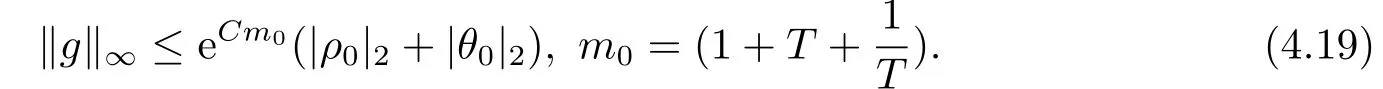
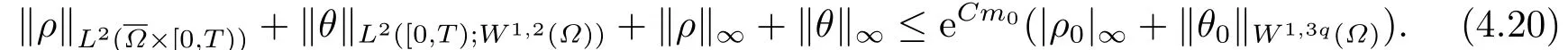

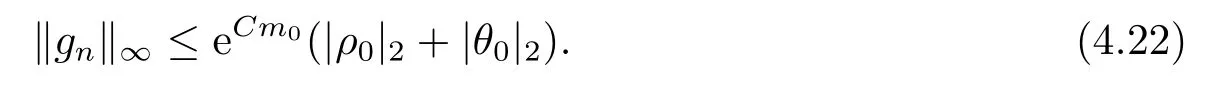
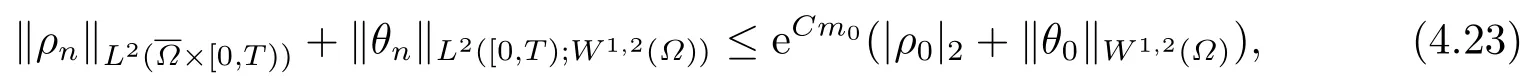



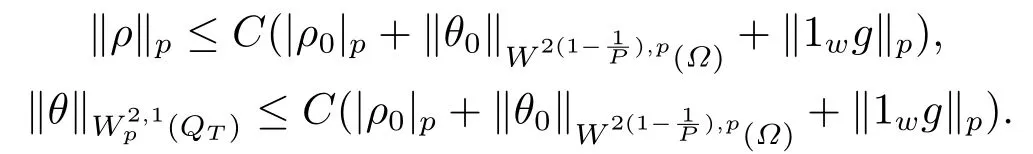
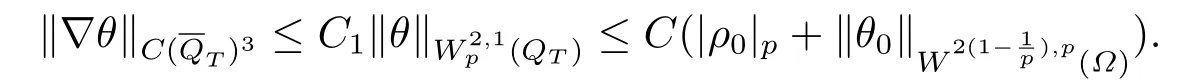

5.时间最优控制的存在性