一类含Hardy-Leray势的分数阶p-Laplacian方程解的单调性和对称性
2022-01-19蒋艳琳沃维丰
蒋艳琳, 沃维丰
(宁波大学数学与统计学院, 浙江 宁波 315000)
1.引言
本文主要研究含Hardy-Leray势的分数阶p-Laplacian方程
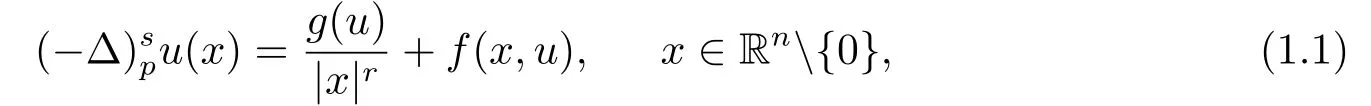
其中sp < r < n,0< s <1,p >2,(−Δ)是分数阶p-Laplacian算子, 这个非局部算子的定义为:

这里的PV代表柯西原理值,Cn,sp是一个依赖于n,s,p的正常数.为使积分有意义, 本文要求u(x)
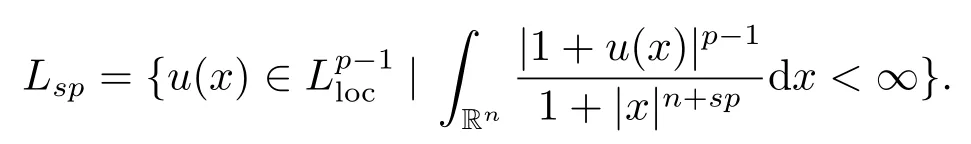
当p=2,r=2s时, 方程(1.1)为

Barrios等[1]证明了方程(1.2)在有界域上正解的单调性和对称性.HU[2]运用了完全不同的方法证明了此方程在有界域上正解的单调性和对称性.此外, 近年来国内外对含Hardy-Leray势的椭圆型方程解的存在性、单调性、对称性以及渐近性行为也取得了许多研究成果[3−6].
由于分数阶Laplacian算子的非局部性, 对它们研究存在困难.为了解决此问题, Caffarelli和Silvestre采用了将非局部问题简化为更高维的局部问题的方法[7].另一个方法则是积分方程法[8−10], 即在建立了分数阶方程与积分方程的等价性后, 采用积分形式的移动平面法,得到分数阶方程解的对称性.但运用上述方法, 对研究分数阶p-Laplacian是不起作用的, 因此CHEN等采用了直接的移动平面法, 建立了关于分数阶Laplacian的极值原理、窄域原理以及无穷远处衰减定理[11], 使得不经过空间延拓和积分方程的方法就可以研究各种非局部问题正解的单调性和对称性等.之后, 在文[12]中他们研究了关于分数阶p-Laplacian算子的极值原理和边界估计, 并得到了方程

在单位球和全空间上正解的单调性和对称性.后来, 许多学者应用了他们的方法研究了其他问题解的单调性、对称性和不存在性等[13−18].
其中, 文[15]中定理1.1证明了关于分数阶p-Laplacian问题的窄域原理.文[16]研究了分数阶p-Laplacian方程的衰减定理, 并推广了(1.3), 得到了方程(−Δ)(x) =f(x,u,∇u)在有界域和全空间上正解的单调性和对称性.
本文基于相关研究结果, 运用直接的移动平面法, 依托窄域原理、无穷远处衰减定理和边界估计, 通过在给定方向上移动平面至极限位置, 比较方程在两个不同点上解的值, 研究了方程(1.1)正解的单调性和对称性.
2.准备工作
本节介绍一些文中用到的相关定义、假设和引理.
首先, 引入一些定义、记号和假设.令x=(x1,x2··· ,xn)=(x1,x′).定义
Tλ={x ∈Rn|x1=λ,λ ∈R}
是Rn上的一个超平面, 并且
Σλ={x ∈Rn|x1<λ}
是超平面Tλ左边的区域.设
xλ=(2λ −x1,x′),
0λ表示原点0关于Tλ的对称点.Ci(i ∈N)表示一致常数.令u(xλ)=uλ(x),为了比较u(x)与uλ(x)的值, 定义
wλ(x)=uλ(x)−u(x).
在本文的定理中,对于f(x,u),g(u)有以下三个条件:
(h1)f(x,u)和g(u)是关于u局部Lipschitz连续的, 且g(u)是非负函数;
(h2) 当λ<0,x ∈Σλ, 且u ∈[0,∞)时,f(x,u)≤f(xλ,u);
(h3) 当λ=0,x ∈Σλ, 且u ∈[0,∞)时,f(x,u)=f(xλ,u).
下面将介绍本文所需的引理.
引理2.1[1](窄域原理) 设Ωλ是Σλ内的有界狭窄区域, 且包含在{x|λ −β < x1< λ}中,β是常数.假设u(x), 且wλ(x)是上的下半连续函数, 满足
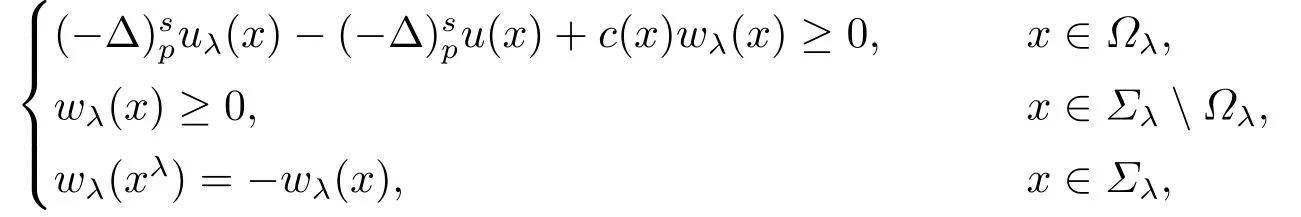
其中c(x)在Ωλ中一致下有界.
若存在一个点y0∈Ωλ, 使得wλ(y0)>0, 则对于足够小的β, 有
wλ(x)≥0,x ∈Ωλ.
进一步, 若对于Ωλ中的某个点y′, 使得wλ(y′)=0, 则
wλ(x)≡0,x ∈Rn.
对于一个无界区域, 如果进一步假设:
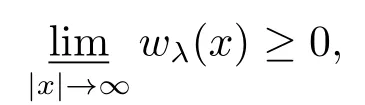
那么上述结论依然成立.
引理2.2[4](无穷远处衰减定理) 设Ω是Σλ中的无界区域,u(x)且wλ(x)是上的下半连续函数, 满足
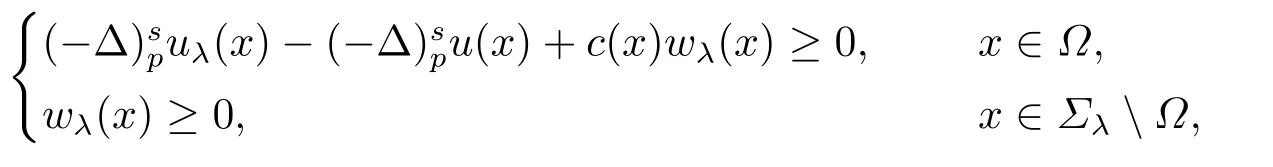
其中
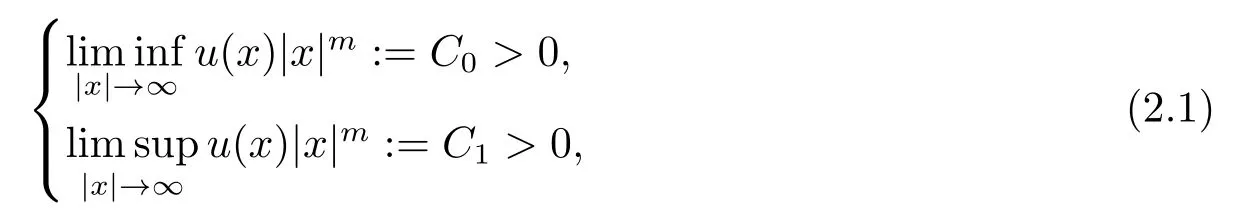
这里的m是正常数.若
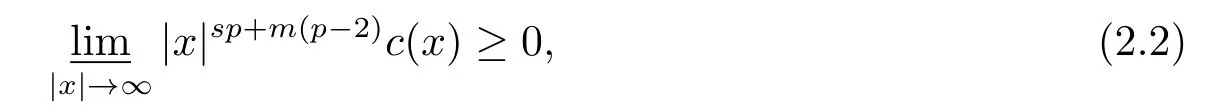
则存在一个正常数R0(依赖于c(x)和C0), 使得如果wλ(x0)=<0, 那么

引理2.3[12](边界估计) 设wλ0(x)>0,∀x ∈Σλ0.对于序列{λk}和{xk}, 若λk ↘λ0, 并且xk ∈Σλk, 使得
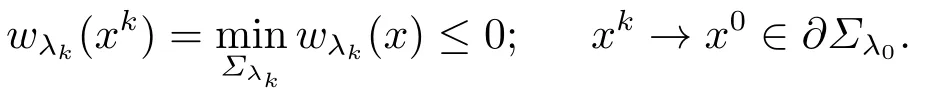
令δk=dist{xk,∂Σλk}≡|λk −, 那么
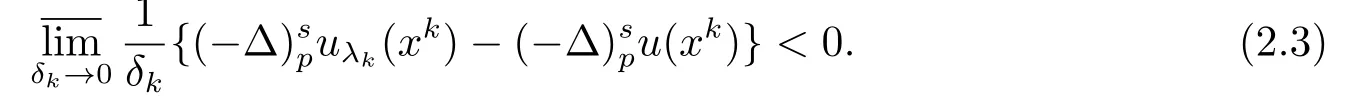
3.主要结论
定理3.1Ω是Rn上包含原点的有界开区域, 在x1方向上是凸的, 且关于T0={x ∈Rn|x1=0}对称.设u(x)是方程
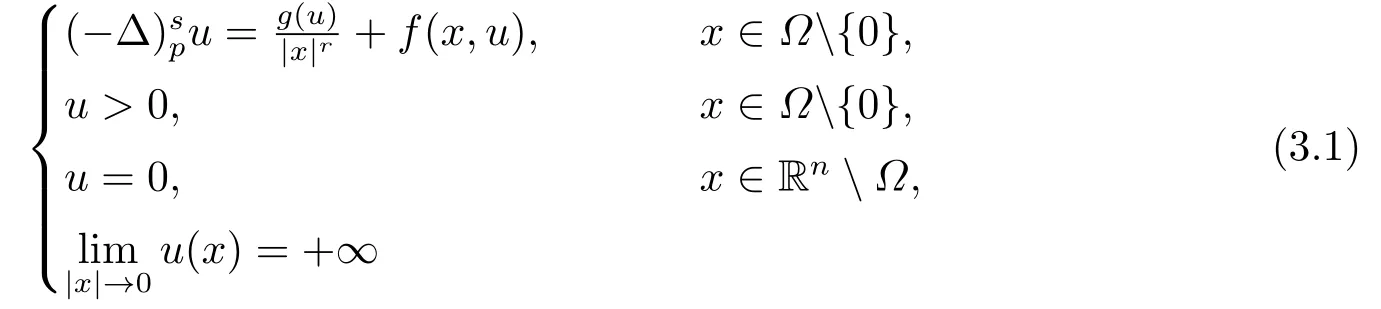
的正解, 若f(x,u),g(u)满足条件(h1),(h2), 则有

且当x1<0时,u(x)是关于x1严格单调递增的.若f(x,u)进一步满足条件(h3), 那么u(x)是关于T0对称的, 即u(x1,x′)=u(−x1,x′).
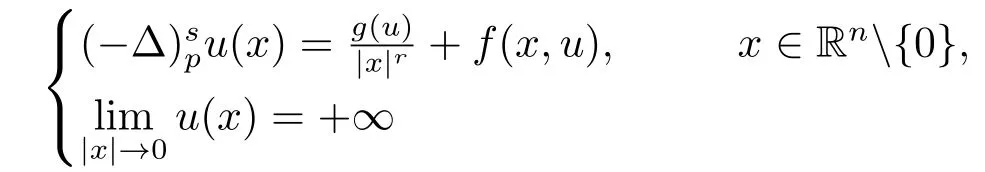
定理3.2设u(x)是方程的正解, 并满足条件(2.1), 其中若f满足
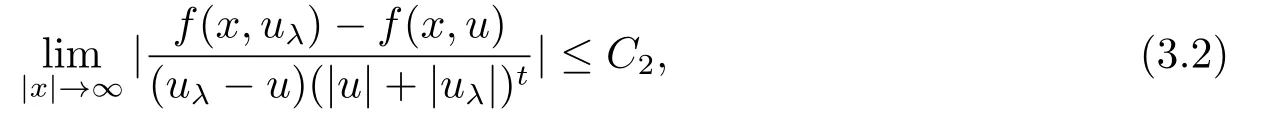
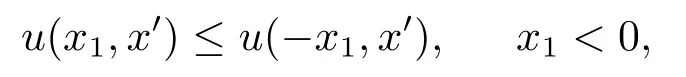
且当x1<0时,u(x)是关于x1严格单调递增的.若f(x,u)进一步满足条件(h3), 那么u(x)是关于T0对称的.
在第四节和第五节将给出定理3.1与定理3.2的证明.
4.定理3.1的证明
证定义Hλ=Σλ ∩Ω.不妨假设证明分为以下两步.
步1 让λ充分接近−a, 即存在足够小的δ(0< δ < β), 使得λ ∈(−a,−a+δ], 且0λ不在Hλ中, 则可以得到



令
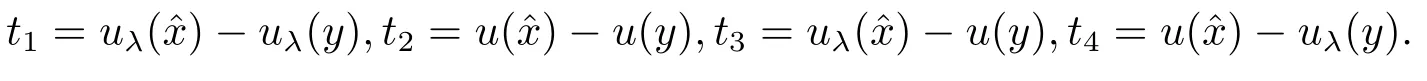
故
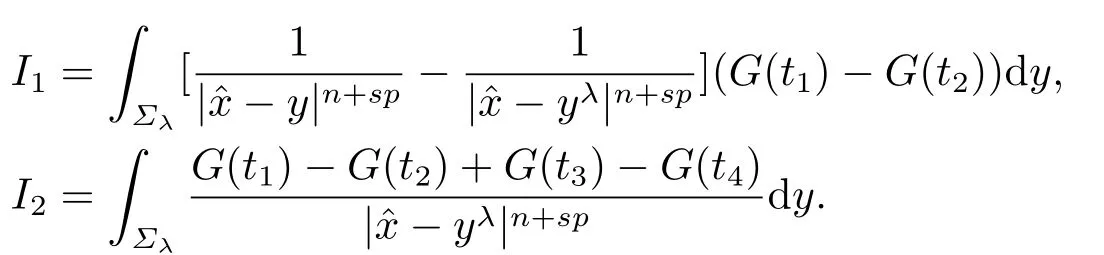


与此同时, 对于任意的y ∈Σλ,∈Σλ, 有

其中ζ(y)介于y与yλ之间, 因此根据引理2.1的证明可知存在正常数C3, 使得

对于I2,

其中ξ(y)介于t1和t4之间,η(y)介于t2和t3之间.结合(4.2), (4.5)与(4.6), 有
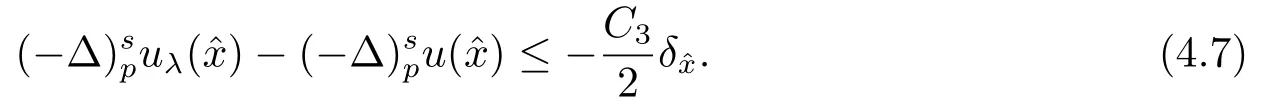
假设f(x,u)和g(u)满足条件(h1),(h2), 则存在正常数C4,C5, 使得对于任意的x ∈Hλ, 有

令

则对于x ∈Hλ,c(x)是有界的, 故
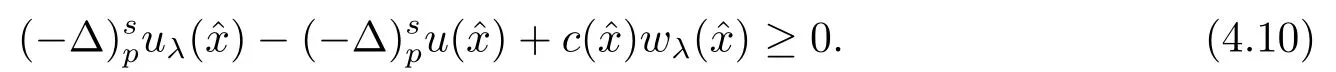

再由(4.9), 可得
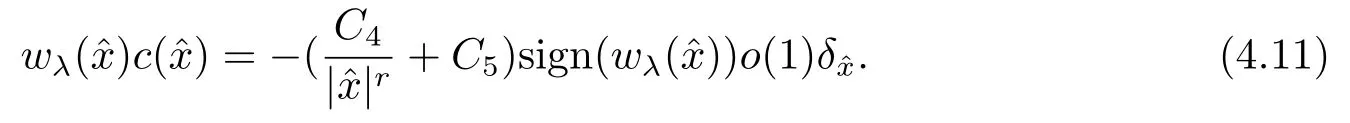
结合(4.7)和(4.11)可知, 当δ足够小时, 有
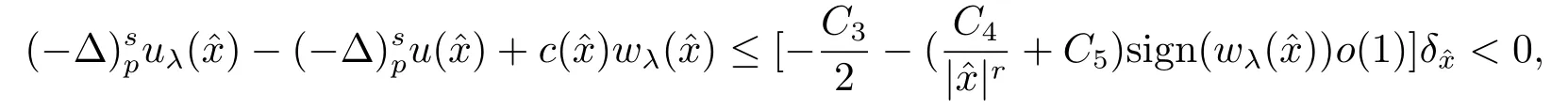
这与(4.10)矛盾, 故(4.1)成立, 因此
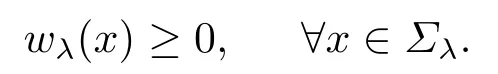

可以证明

若(4.12)不成立, 则λ0<0.事实上, 首先可以证明
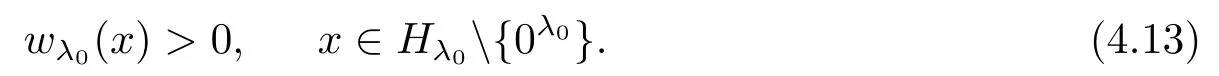


但是, 由(4.8)可知
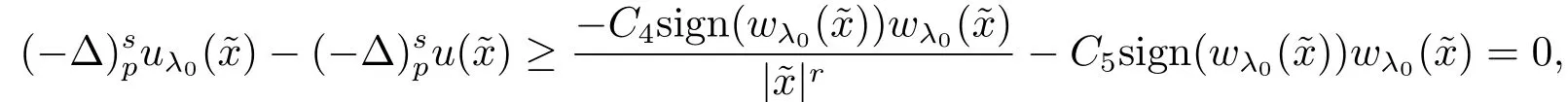
这与(4.14)矛盾, 则(4.13)成立.
由λ0的定义可知, 存在序列{λk}和{xk}, 有0≥λk ↘λ0, 并且xk ∈Hλk{0λk}, 使得
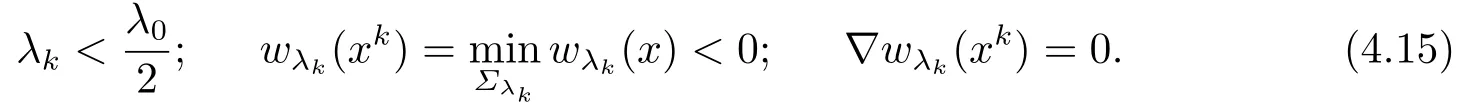
因为|xk|是有界的, 所以对于{xk}的子列(仍记为{xk}), 存在x0使得xk →x0.由(4.15)可知wλ0(x0)≤0, 则

于是, 当k →∞时, 有

因此, 根据(4.8),(4.9)和(4.16)可知, 当k →∞时,δk →0, 有
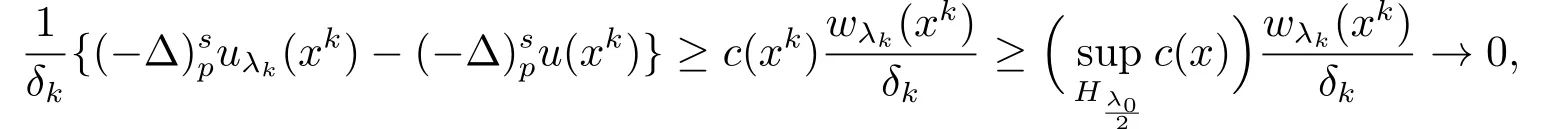
这与引理2.3矛盾, 故(4.12)成立, 于是
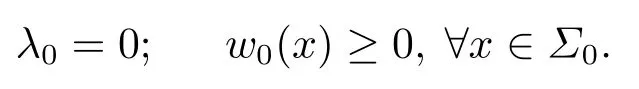
再根据(4.13)的证明可知, 当x1<0时,u(x)是关于x1严格单调递增的.
若f(x,u)进一步满足条件(h3), 则可以证明u(x)在x1方向上是关于T0对称的.事实上, 根据以上的证明可知

再由(h3)的假设,则(x1,x′):=u(−x1,x′)也是问题(3.1)的解,故(x1,x′)≤(−x1,x′),x1<0,即
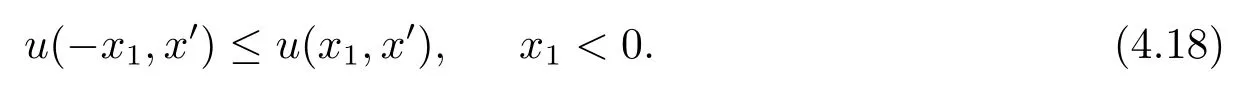
结合(4.17)和(4.18)有
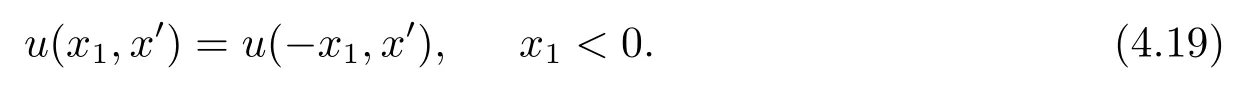
至此, 定理3.1证毕.
5.定理3.2的证明
证证明分为以下两步.
步1 证明存在一个常数R0>0, 使得对于λ<−R0, 有


假设f(x,u)和g(u)满足条件(h1),(h2), 根据(4.10)的证明, 有
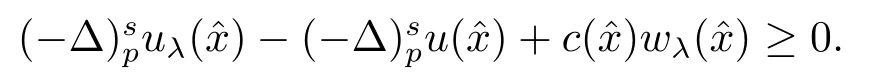

则条件(2.2)成立.因此根据引理2.2可知, 存在常数R0>0, 使得|ˆx| ≤R0, 对于λ ≤−R0,有(5.1)成立, 即


可以证明

否则, 对于λ0<0, 首先根据(4.13)的证明(这里的x所在区域与其不同, 但证明思路相同,故过程省略), 可得
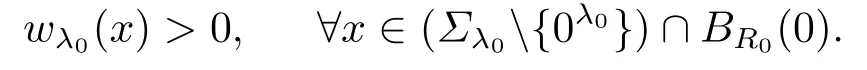
由λ0的定义可知, 存在序列{λk}和{xk},有0≥λk ↘λ0, 并且xk ∈(Σλ0{0λ0})∩BR0(0),使得
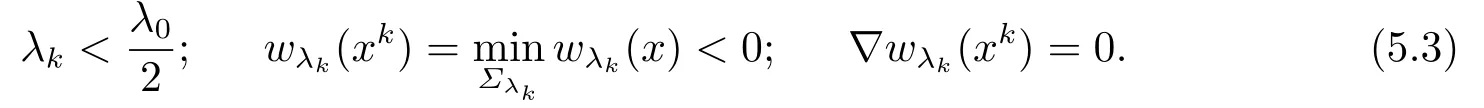
因为|xk| 于是, 当k →∞时,δk →0, 有 这与引理2.3矛盾.故(5.2)成立, 于是 再根据(4.13)的证明可知, 当x1<0时,u(x)是关于x1严格单调递增的. 若f(x,u)进一步满足条件(h3), 根据(4.19)的证明, 可以得到u(x)在x1方向上是关于T0对称的.至此定理3.2证毕.

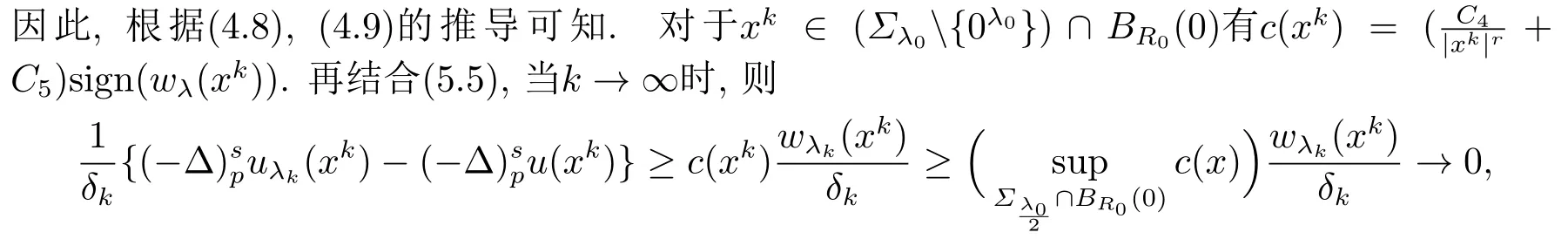

猜你喜欢
杂志排行
应用数学的其它文章
- Atomic Decomposition of Weighted Orlicz-Lorentz Martingale Spaces and Its Applications
- Solvability of Mixed Fractional Periodic Boundary Value Problem with p(t)-Laplacian Operator
- 一类非线性趋化方程的能控性及时间最优控制
- Existence of Positive Solutions for a Fractional Differential Equation with Multi-point Boundary Value Problems
- 奇异椭圆方程Robin问题多重正解的存在性
- A Higher Order Wolfe Converse Duality in Multiobjective Programming with Cone Constraints
