指向抽象思想培养的小学数学试题命制

陈小英

（霞浦县第四小学，福建 霞浦 355100）

试题检测一直是考查学生学习目标是否达成的主要手段。合理的命题有利于考核学生的阶段学习成果，反馈教师的教学效果，从而优化教师的教和学生的学，提升教学质量。近年来，小学数学命题改革从“双基”向“四基”发展，不仅重视学生基础知识、基本技能的掌握情况，还关注到学生基本思想的渗透和基本活动经验的积累。抽象、推理和模型是数学的三大基本思想，其中抽象思想又是这三大基本思想中最核心的思想。史宁中教授认为，数学在本质上研究的是抽象的事物，教学的最终目标也是培养学生具有初步的抽象能力。［1］抽象能力是一种重要的科学研究能力，是一个人智慧的表现。如何优化命题的价值取向，以“抽象”这个基本的数学思想来导向命题策略，通过合理地命题，培养学生抽象能力呢？

一、依托生活素材，抽象数学问题

数学与生活联系紧密。在命题时，把自然、社会、生活中与数学有关的因素作为素材，让数学与生活在命题中“友好牵手”，一直都是命题改革发展的趋势所在。生活问题富含生活味，包裹着各色各样华丽的生活外衣，它与学生在课堂上学习的数学问题是不能完全等同的。将生活问题抽象成数学问题，是学生解题前的关键步骤，同时也是培养学生抽象能力的有利抓手。只有通过阅读、想象、分析，剔除生活问题中的无关因素，选取有用的数学信息，才能抽象成数学问题。这一个抽象化的过程，有利于学生建立抽象思想，发展抽象能力。

试题1：霞浦县游泳馆内有一个长40 米，宽30 米，池深约2 米的游泳池。（1）工人师傅要在游泳池的底部贴上地砖，你认为买以下哪种型号的地砖比较合适，无需裁剪？需要买多少块地砖？A 型地砖：边长5分米；B 型地砖：边长6 分米。（2）游泳池里水深约1.2米，如果每周换一次水，每次换水大约多少升？（3）工人准备用绳子将游泳池隔成长40 米，宽2 米的若干泳道，请你算一算，至少要用绳子多少米？

由生活素材创设的情境，比枯燥的数学问题更生动。面对熟悉的生活情境，有利于激发学生的解题兴致，激活已有经验。此题表面上是给游泳池贴地砖、换水和做隔离带的生活问题，实际上，游泳馆是长方体，题（1）贴地砖是有关公因数知识的应用问题；题（2）给游泳池换水是求长方体的容积问题；题（3）给游泳池做隔离带，包含间隔排列和整数乘法的问题。将生活问题抽象成数学问题，只是解题时的第一次抽象，接着还要在数学问题中抽象出数量关系，用数学语言来表达，进而解决问题。熟悉的生活素材为学生抽象数学问题提供正向刺激，使学生在积极的心向中达成对问题的抽象与解决，亲身感悟数学抽象思想。

二、借助图像呈现，抽象思考方法

数学学科具有很强的抽象性，也最能体现思维能力。抽象思维反映数学学习的高层次水平，是创新性学习的主要体现。小学生以具体形象思维为主要思维形式，如何助推学生思维向抽象发展、感悟抽象思想呢？在试题设计中，可将试题与图像携手呈现，丰富试题内涵。图像指的是图形、图画、表格等。学生在答题时，首先要摒弃图像中的无关因素，搜集有关信息；接着将搜集到的有关图像信息转化为数学语言，将图像信息与文字信息联合起来，观察、分析、抽象、概括，直至解决问题。学生的解题过程也是抽象思维孕育生长的过程。

试题2：如图1，把0°到180°平均分成4 份，A、B、C、D 四点表示不同的角度，其中（ ）点的角度大小等于直角三角形中两个锐角度数之和。

图1

这是“直角三角形知识”与“数轴”的综合应用。在直观图上，学生要自觉将二维平角的角度抽象为一维线段的长度，将角度与数轴上的位置一一对应，然后利用已有的知识经验，开展思维推理活动。线段表示0°到180°的角，平均分成4 份，可以推导出每一份表示45°，那么点A 所在的位置表示的是45°的锐角，点B 表示直角，点C 表示大于90°而小于180°的钝角，点D 表示平角。从文字信息中得出答案是直角，所以正确选项是B。学生经过练习，深化对直角三角形相关知识理解的同时，感悟到这种有条有理、有根有据思考方法的价值。

试题3：“垃圾分类”社团小组对班级学生进行调查，并绘制以下的统计图表（如图2），你能结合图表中的信息，求出b=（ ）吗？

图2

此题把信息融入图表中，需要学生认真阅读图表，将图表中的信息抽象为数学语言，然后对试题进行推理分析和解答。统计图表上的已知信息有：①非常了解的人数是18，占全班总人数30%，②基本了解的有30 人。要求解答的问题是：b（不了解的人数所占的百分比）等于多少？此题可以先求出全班总人数18÷30%=60（人），接着求出b=（60-18-30）÷60=20%；也可以先求出基本了解的人数所占的百分比：a=30%÷18×30=50%，故b=1-30%-50%=20%等。学生经历一系列的解题过程，思维能力逐步由直观思维向抽象思维发展。

三、应用多元表征，抽象知识模型

“表征”指信息的记载或者表达的方式。在数学学习中，“表征”指学生用自己的方式表达对数学知识的理解。在解题过程中，引导学生从不同的视角出发，对知识进行多元化表征，有利于学生逐步剥离数学知识的非本质属性，获得对知识内涵的理解和知识外延的把握，逐步抽象出知识模型，提升抽象能力。

试题4：图3 中三角形和小棒的数量是相等的。先数一数图中有（ ）个三角形，画一画缺少的小棒根数，然后在计数器上用算珠表示出它们的数量，最后填空。

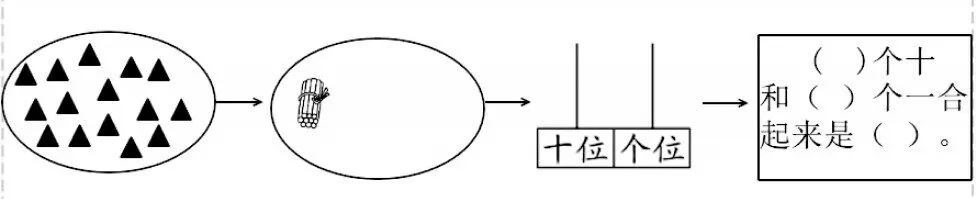
图3

此题要求学生从数出15，到补画15，再到计数器上拨出15，最后用语言描述出15 的组成。15 个三角形可以表示15，10 根小棒加上5 根小棒可以表示15，用十位上的1 颗珠子和个位上的5 颗珠子也可以表示15，不管哪种表征形式，只要是1 个十和5 个一合起来的数都是15。表征由简单变为复杂，直到抽象，学生从丰富的渐进式表征中体会到知识之间的勾连，抽象出立体、饱满的两位数的知识模型。［2］

（1）画：我会画图来表示。（2）说：本题是要把（ ）朵小红花看作单位“1”，平均分成（ ）份，送给乐乐的小红花占其中的（ ）份，也就是（ ）朵。（3）算：我会列式计算。（4）编：我会编这样列式解答的数学问题。

单一的表征形式不利于体现学生对知识理解的全面性。学生在解题中，循着知识脉络发展特点和自身认知生长特点，逐层进行不同方式的表征，从直观形象的图像表征到抽象的语言表征、符号表征，逐步触摸内化知识本质，抽象出“求一个数的几分之几是多少”要列乘法算式来解答的知识模型。模型抽象出来后，建模过程并未停止，题（4）改变问题的情境，让学生将初步建立的知识模型应用到实际中，促使模型内涵得到深化，模型外延得到拓宽，从而建立更加完善的结构化知识模型。