易腐食品生产的质量和成本双目标优化:以乳制品为例

詹沙磊 王海燕∗ 陈达强 左 超 高国亮

(1.浙江工商大学 管理工程与电子商务学院, 浙江 杭州 310018; 2.浙江食药质量安全工程研究院, 浙江 杭州 310018)

0 引言

近些年来,易腐食品质量安全事故时有发生,易腐食品质量安全问题引起了社会的普遍关注[1-2]。在供应链中,易腐食品需要经过原材料供应、生产加工、储存运输等环节,最终抵达消费者区域,这个过程被比喻为从农场到餐桌的过程[3-4]。在该过程中,不合适的储藏方法、不充分的卫生标准、以及滥用农药等都会造成食品质量安全风险[5]。在易腐食品生产过程中开展适当的质量改进活动,是解决易腐食品质量安全问题的有效方法[6]。但质量改进活动需要消耗成本的,且成本总量往往是有限的[7]。因此,研究如何权衡易腐食品质量改进和成本消耗的质量改进决策优化问题,具有重要意义。

与一般制造业产品不同,易腐食品,顾名思义,具有易腐性的特点[8]。在构建决策优化模型时,决策者将会面对易腐食品的质量演变的随机性和动态性难题。随机性源于易腐食品质量评价的不确定性,它与感知属性、隐藏属性等多种属性相关[2]。而且意外污染和变质可能发生在易腐食品生产和运输的任何阶段,这也增加了易腐食品质量演变的随机性[9]。动态性则源于多种质量改进活动的选择,因为不同的质量改进活动,既会消耗不同的成本,又会导致不同的质量改进效果[10]。然而,在已有的研究中,大多数学者仅考虑易腐食品质量演变的动态性,比如设计一个瓶颈质量退化方程[11],提出一个最小剩余保质期[12],设计一个时间变化的质量分段函数[13-14],以及定义一个最佳保鲜温度范围[15]等。但是这种动态性只能反映质量的被动变化,未考虑质量被质量改进活动影响后的主动变化。而且,考虑易腐食品质量演变的随机性的研究更少。鉴于此,本文拟同时考虑易腐食品质量演变的动态性和随机性,研究易腐食品生产过程中的质量改进决策优化问题。

在研究方法的使用上,多目标优化方法[16-17]、多准则决策方法[18]、博弈论方法[5-6,19-20]以及启发式算法[14,21]都是常用的质量改进决策优化方法。考虑到易腐食品质量演变过程的随机属性,随机规划方法更加适合易腐食品质量演变的建模和优化问题。GERT(Graphic Evaluation and Review Technique,图示评审技术)是网络理论、概率论、模拟技术、信号流图等理论方法的结合体,是一种新型的随机网络方法,其自带的随机网络参数可以很好地诠释易腐食品质量演变的随机属性[22-23]。贝叶斯方法则综合利用了易腐食品质量改进前的参数先验信息与拟采取的质量改进决策信息,可以很好地演示易腐食品质量受质量改进决策影响后的动态性[24-25]。因此本文拟采用GERT随机网络方法与贝叶斯方法相结合的研究方法,选取一种典型的易腐食品——乳制品为例,将乳制品生产过程看成一个GERT网络,将乳制品质量的演变受质量改进决策的影响设计成贝叶斯更新过程,在此基础上构建乳制品质量和成本双目标协调优化模型,并寻求成本与质量之间的平衡。

1 乳制品生产过程质量演变的GERT网络

某种乳制品生产过程(见图1)主要包括三个子过程:灌装乳生产、辅物生产、以及包装生产。其中,灌装乳生产过程中没有逆向流和自环流,因为对灌装乳的质量控制比较严格,不合格的在制品即被淘汰,不会对其进行再利用;而辅物和包装生产过程中存在自环流,允许对辅物和包装进行再加工。

图1 某种乳制品生产过程Figure 1Production process of a dairy product

基于该乳制品生产过程的视角,构建如图2所示的乳制品生产过程中的质量演变GERT网络。记所有节点的集合为J。节点1~11与乳制品生产过程的各个环节一一对应。随着质量的产生、传递和累积,除了节点8和节点10,每一个环节输出的质量都有合格与不合格两种结果。因此还需增加节点12,代表不合格品的废弃处理环节。节点8和节点10除了输出质量合格的部分与质量不合格的部分之外,还输出再加工的部分(假设再加工的部分与首次加工是无区别的)。记i和j是任意的两个相邻节点,(i,j)代表一条始于i终于j的弧线。每一条弧线代表不同质量水平的在制品的质量传递活动。如弧线(1,2)表示节点1输出的合格品的质量传递活动,弧线(1,12)表示节点1输出的不合格品的质量传递活动。因为乳制品生产过程中的质量演变具有随机属性,所以节点输出的质量也具有随机性质。假设每一条弧线上存在一对网络参数:(概率、成本)。用(pij,qij)来表示弧线(i,j)上的网络参数。其中pij为弧线(i,j)的质量传递概率,在这里代表在制品的质量合格率(流向下一个生产节点)、或质量不合格率(流向废弃处理节点)、或再加工率(专门用于节点8和10的自环弧线)。qij为弧线的成本,不失一般性,在这里代表每一单位在制品在弧线(i,j)上的生产成本(或再加工成本、废弃处理成本),假设其是连续型随机变量、服从正态分布且参数已知,即

图2 乳制品生产过程质量演变的GERT网络Figure 2GERT network for quality evolution of dairy product production process

节点输出的质量不仅具有随机性,而且具有动态性。这种动态性在于每一个节点输出质量的测评指标可分为感官指标(包括外观、重量、气味、味道等)和隐藏指标(包括理化指标、微生物指标等)[26]。与之相对应,质量的影响因素包括人力资源、机器设备、生产原料、工艺流程、环境状态(即人机料法环)[27]。为改进节点输出的质量水平,可从质量影响因素人机料法环的角度罗列出若干个质量改进活动。比如在奶牛输出原乳时,可以采取的改进活动有草料检测、畜类药物检测等,以及这些改进活动的组合。记节点i的质量改进活动为ωi,节点i所有质量改进活动的集合为Ωi,则ωi∈Ωi。一方面,节点i的质量改进活动ωi会提高弧线(i,j)的质量合格概率pij,另一方面也会增加弧线(i,j)的成本qij(这里“增加成本”可以理解为质量改进活动的实施是需要成本的,这种成本被计入到最终产品的售价中。如:一瓶采用了更先进消毒技术的牛奶比采用普通消毒技术的牛奶卖得更贵)。可见,质量改进活动的采用会导致“质量改进”和“成本增加”正反两种结果。因此,需要建立一个双目标优化模型对这两种结果进行权衡分析。

2 质量改进策略对网络参数的贝叶斯更新

考虑到质量改进活动的效果的两面性,决策者需要决定是否采取质量改进活动(Whether)、以及采取怎么样的质量改进活动(How)。定义两类决策变量:一是定位变量zi,表示是否对节点i进行质量改进,zi是0-1变量,取1表示采取、取0表示不采取;二是指派变量xωi,表示是否在节点i采取活动ωi,xωi也是0-1变量,取1表示采取、取0表示不采取。两类决策变量之间的关系表达式如下:

2.1 质量改进策略对概率的贝叶斯更新

假设弧线(i,j)的发生与活动ωi存在可以量化的相关关系,且弧线(i,j)的发生受到活动ωi影响的可能性可以用似然函数来表示。由贝叶斯定理可知:后验概率可由先验概率和似然函数运用贝叶斯公式算得。因此,参考文献[25]中有关离散型随机变量的概率更新的贝叶斯公式,计算出弧线(i,j)发生的后验概率πij为

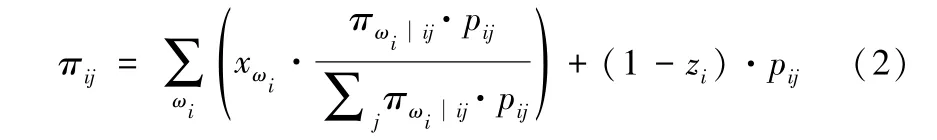
上式将质量改进策略整合到传统的贝叶斯公式中,当存在质量改进活动(即zi等于1)时,右式即是根据贝叶斯公式得到的后验概率值;当不采取质量改进活动(即zi等于0)时,右式为原来的先验概率值(即没有发生更新)。

2.2 质量改进策略对成本的贝叶斯更新

假设弧线(i,j)的成本qij与质量改进活动的成本cωi存在可以量化的相关关系,可以用似然函数

来表示:

参考文献[24]中有关连续型随机变量的概率更新的贝叶斯公式,首先计算出cωi的边际概率分布函数为

继而计算出弧线(i,j)的后验成本cij:

其中

以及

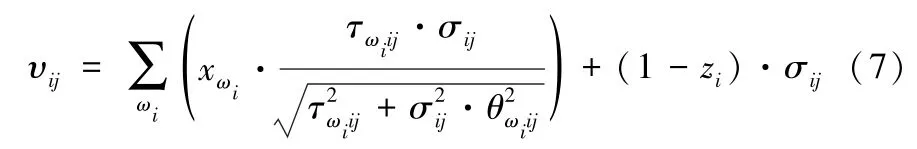
以上两式将质量改进策略整合到传统的贝叶斯公式中,当存在质量改进活动(即zi等于1)时,右式即是根据贝叶斯定理得到的后验成本均值和标准差;当不采取质量改进活动(即zi等于0)时,右式为原来的先验成本均值和标准差(即没有发生更新)。

3 乳制品生产过程质量改进策略优化模型

3.1 目标函数

为了对质量改进活动的两种结果(质量改进和成本增加)进行权衡分析,本文建立两个目标函数:质量水平最大化目标G1和成本最小化目标G2,分别如式(8)和(9)所示。

质量水平最大化目标旨在追求一单位最终产品的质量水平的最大化。因为最终产品由四种原材料(即原乳、矿物质、果蔬物质、包装原材料)生产得到,它们到最终产品的质量水平分别由四种原材料到最终产品的等价后验概率来表示,记为Eπ1,11、Eπ5,11、Eπ6,11和Eπ9,11,所以将该目标设计为最大化四种原材料到最终产品的等价后验概率的总和。

同理,成本最小化目标旨在追求一单位最终产品的总成本的最小化。因为一单位最终产品的总成本是由一系列生产过程累积过来的(或者可以理解成总成本可拆解成各个生产过程的子成本)。记Ec1,11、Ec5,11、Ec6,11和Ec9,11为四种原材料到最终产品的等价后验成本,则该目标为最小化四种原材料到最终产品的等价后验成本的总和。

等价后验概率和等价后验成本可利用后验矩母函数、后验传递函数、梅森增益公式等公式来算得,具体如下。

3.2 后验成本的矩母函数

在概率论和统计学中,随机变量的矩母函数是其概率分布的一种技术指标。由于本文的随机变量(即成本)是经过质量改进策略A影响后的后验成本,因此其矩母函数是一个特殊的矩母函数。

定义1 令Mij(A,s)为后验成本cij的矩母函数,则该矩母函数称为后验矩母函数,其公式为

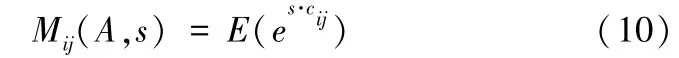
其中,s表示任意实数。由于本文中后验成本cij是连续型的随机变量,所以上式等价于

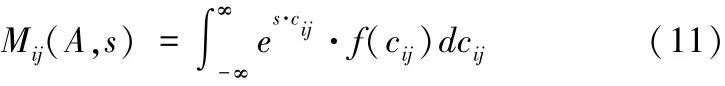
3.3 集成后验概率和后验成本的传递函数

传递函数的作用是将具有两个网络参数的GERT网络转换为一个与原网络结构相同、但只有一个网络参数的网络,以简化网络参数的复杂性。由于本文的网络参数都是后验网络参数,因此其传递函数也是一个特殊的传递函数。

定义2令Wij(A,s)为弧线(i,j)的传递函数,则该传递函数称为后验传递函数,其公式为

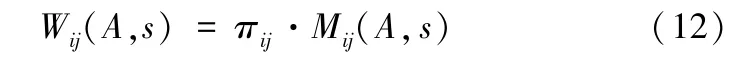
3.4 梅森增益公式

后验传递函数只是集成了相邻两个节点的后验概率和后验成本,当需要求任意两个不相邻节点的等价后验传递函数时,要使用梅森增益公式。梅森增益公式是一种求解线性信号流图传递函数的方法,它将信号流图简化为单一传递函数[22]。记EWm,n(A,s)为任意两个不相邻节点的等价后验传递函数,则梅森增益公式的表达式为

其中,g为前向通路(前向通路是GERT网络图中始于m终于n的一条通路,而且通路上的节点只经过一次)的条数,pmng为第g条前向通路的总增益(前向通路的总增益是组成第g条前向通路的各条弧线的后验传递函数的乘积),Δmng为不与第g条前向通路接触的剩余子图的特征式(特征式是网络图所表示的方程组的系数矩阵的行列式,其计算公式参照整个网络图的特征式计算公式)。Δ是整个网络图的特征式,其公式为

其中,k为回路(回路是起始及终止于同一节点,并与其他节点相遇仅一次的通路)的阶数,k阶回路是指k个互相不接触的回路的集合。h为k阶回路的个数,为第h个k阶回路的总增益(回路的总增益是第h个k阶回路中各个回路的后验传递函数的乘积)。

3.5 等价后验概率和等价后验成本

在获得任意不相邻节点的等价后验传递函数之后,就可以利用后验矩母函数的特性来求得任意不相邻节点的等价后验概率和等价后验成本,以下以始于节点1终于节点11的等价后验概率和等价后验成本为例,其他可参照此例。

3.5.1 等价后验概率

首先根据式(12),可将始于节点1终于节点11的等价后验传递系数EW1,11(A,s)写为

其中,Eπ1,11是始于节点1终于节点11的等价后验概率,EM1,11(A,s)是始于节点1终于节点11的等价后验矩母函数。

根据后验矩母函数的定义,当s=0时,有

将式(16)代入式(15),可得

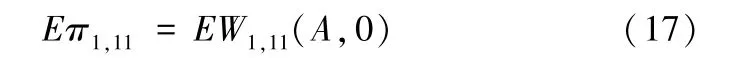
上式求得的即是始于节点1终于节点11的等价后验概率。

3.5 .2等价后验成本

将式(17)代入式(15),再变形,可得

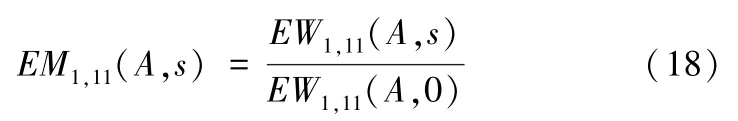
需要注意的是,后验成本cij的后验矩母函数具有以下重要性质:后验矩母函数在s=0时的一阶导数值是后验成本cij的一阶中心矩(即数学期望),即

将式(18)代入式(19),可得

上式求得的即是始于节点1终于节点11的等价后验成本。

4 模型求解

对于求解多目标规划,模糊目标规划方法(Fuzzy goal programming approach)是一种有效方法,它弥补了决策者在使用传统的目标规划法时无法为每一目标函数给出精确目标值的缺陷[28]。考虑到乳制品质量演变的特殊属性,决策者较难为质量和成本设置精准目标值。而模糊目标规划法可以为每个目标设置模糊目标值区间,适合求解该类问题。具体求解步骤如下:

步骤1为两个目标函数分别设定模糊目标值区间从而分别构建隶属函数β1和β2:

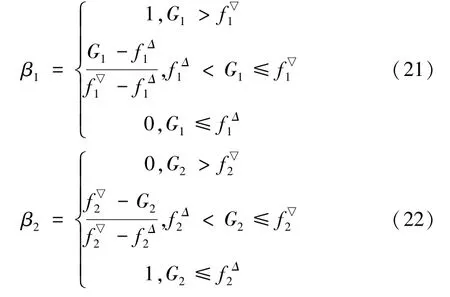
目标隶属函数可以看成是目标接近理想目标值的程度,即理想目标的实现程度。隶属函数值越大,表明目标越接近理想目标,从而理想目标的实现程度越大。

步骤2为两个目标函数分别设定优先级权重λ和1-λ,从而用加权法将原双目标函数转换为新的目标函数F:

步骤3将式(23)作为新的目标值,替代原模型的目标函数,原模型随即转化为单目标整数规划模型。由于模型输入参数“质量改进活动成本cωi”是一个随机变量,其分布函数见式(4),因此需要多次模拟产生cωi的随机数,获得多次目标函数F的求解结果,取平均值作为最终求解结果。

5 算例分析

5.1 算例描述

基于实验室数据的测算和仿真,将本文所提双目标模型和求解方法应用于一个乳制品企业的质量改进算例,以验证模型有效性,并探讨质量和成本的权衡关系。

国内某知名乳制品制造商是一家大型乳制品生产企业,主要从事乳制品生产、销售及相关业务。该企业计划在保持一定质量水平前提下控制乳制品的生产成本,从而为不同质量水平的产品做出差异化的定价策略,因此拟对乳制品生产质量与成本之间进行权衡性分析。已知在乳制品生产过程质量演变的GERT网络中,每个节点(除了两个终端节点11和12之外)有三种质量改进技术,可组合成七种质量改进活动(见表1)。网络弧线的参数值包括质量合格率和生产成本(见表2)。表3为弧线参数与质量改进活动的相关关系数据,每个单元格自上而下分别为这些数据可以通过实验室数据的反复测算和模拟分析得到(如质量合格率与质量改进活动的相关关系数据可通过拉曼光谱仪、MALDI-TOF/TOF质谱仪、以及离子迁移谱仪等测得质量分指标数据,再通过多谱融合技术结合实验室积累的模型库、算法库计算得到综合的质量评价数据;生产成本与质量改进活动成本的相关关系数据可通过两者历史数据或模拟数据的成本比例测算和误差分析得到)。

表1 GERT网络中各节点可采取的质量改进活动Table 1Available quality improvement activities in each node of GERT network

表2 GERT网络中各弧线的网络参数(×0.01)Table 2Parameter values on each arc of GERT network (×0.01)

表3 网络参数与质量改进活动的相关关系数据(×0.01)Table 3Data of correlation between network parameters and quality improvement activities (×0.01)

5.2 算例求解

在CPU为3.2 GHz、内存为4 GB的计算机上,通过Matlab编程求解。取两个目标函数的理想上下界值作为模糊目标值区间的上下界值,设定两个目标函数的模糊目标值区间为[1.74,3.42]和[11.35,16.55];同时,默认两个目标函数的优先级权重相等,即λ=0.5。对“质量改进活动成本”的取值进行了多次模拟,以观测求解结果的稳定性。图3显示了求解20次(每次求解时间为19分钟左右)后的目标函数F、隶属函数β1以及β2的求解结果波动曲线。据此可以进一步求得三者的均值分别为0.63、0.58、0.67以及标准差分别为0.04、0.11、0.12,说明目标函数F相对来说具有更高的求解结果稳定性。而隶属函数β1以及β2的稳定性稍弱于目标函数F。结果表明:在目标函数最优值具有较高稳定性的前提下,由于决策者视质量改进和成本控制两者的重要性并重(因为两者的优先级权重相等),因此可以有多种质量水平与生产成本的组合来满足总目标函数最优的需求(由图3可知,质量水平和生产成本的理想目标实现程度存在此消彼长的矛盾关系,高质量水平对应高生产成本,反之亦然),两者的取舍取决于决策者的态度。

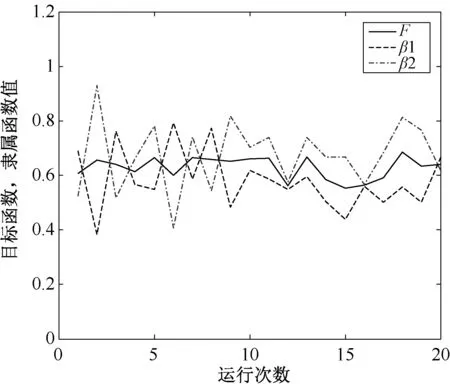
图3 质量改进活动成本模拟20次的求解结果Figure 3Solution results after twenty-time simulation on costs of quality improvement activities

5.3 质量和成本的权衡分析

为了探讨乳制品质量和成本之间的关系,本节通过改变权重λ的取值,来分析模型求解结果的变化。图4显示了当λ的取值由0.1逐渐变到0.9时,目标函数F、隶属函数β1以及β2的变化曲线。由图4所示,λ的取值由小增大意味着质量改进目标的重要性越来越大,而成本控制的重要性越来越小,因此从整体上看β1曲线呈“上坡”状,而β2曲线呈“下坡”状,符合决策者的态度。

在绘制图5之前,作者将每个节点的质量改进活动按照其期望成本进行排序,并赋予编号(0表示不采取质量改进活动),编号越大的质量改进活动其成本越高、技术复杂性越高,所带来的质量改进效果也越大。

由图5可知,λ的取值影响到质量改进活动的选择。图5的z坐标轴的刻度即是质量改进活动编号的刻度。显然,当质量改进越来越重要、同时成本控制越来越不重要时,质量改进活动的选择更为多样化,决策者会不惜成本代价地改进质量水平,质量改进的效果也更高。在本文的算例中,即使在最重“利”忘“质”的λ=0.1时,仍然有少数质量改进活动被采取了,而且集中在节点3—7,即罐装乳生产环节和辅物的生产环节,这些环节应被赋予其较高的质量改进优先级。因此我们认为,在预算有限的情况下,决策者应重点选择与可食用原材料生产有关的环节进行质量改进。

图5 权重取值发生变化时质量改进策略的变化Figure 5Variations of quality improvement strategies when the weight value changes

为了进一步判断各个环节的质量改进优先度、技术难度以及经济性,我们对权重取值发生变化时的质量改进策略做一个统计性分析(如表4所示)。其中,“采取质量改进活动的次数”一栏表示的是当权重取值发生变化时,节点有采取质量改进活动的次数,可反映节点的质量改进优先度;“三个技术同时被采用的次数”是指活动7被选择的次数,可反映对节点进行质量改进的技术难度;“质量改进策略的平均编号”是指节点采取的质量改进活动的编号的平均值,可反映节点进行质量改进的经济性。

由表4的数据可以得到以下管理学启示:

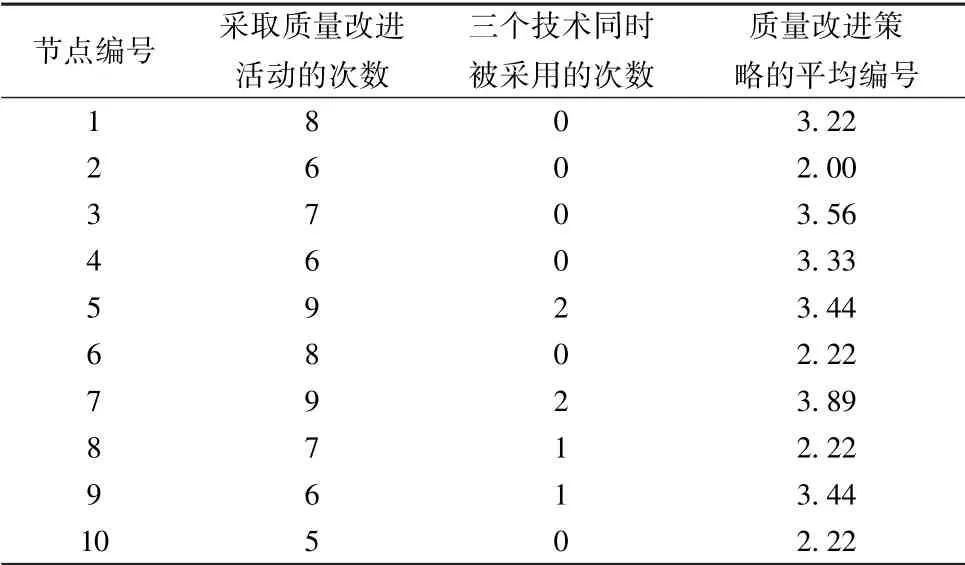
表4 权重取值发生变化时质量改进策略的统计性分析Table 4Statistics analysis of quality improvement strategies when the weight value changes

(1)节点5和7在权重取值发生任何变化时,都有采取质量改进活动。节点5和7对应“矿物质”和“混合物质”环节,说明辅物的原材料质量非常重要,其质量改进的优先度最高。

(2)在质量改进活动的选择上,节点5和7分别都进行了2次具有最高技术难度的质量改进活动。说明辅物的原材料的质量改进难度最大,也侧面说明了其质量安全风险较大。

(3)节点3和7的质量改进的经济性最差,说明对“液态乳”的处理和“辅物混合物质”的处理需要花费较大的成本。

以上三个启示也进一步验证了罐装乳生产环节和辅物生产环节的质量改进关键性。

6 结束语

易腐食品生产质量和成本的最优化是互为冲突的目标,本文将两者进行权衡分析,作为评价易腐食品质量改进策略优劣的标准。本文主要的创新点在于使用贝叶斯方法来演示随机环境下质量改进策略对易腐食品生产过程质量演变的GERT网络参数的改进效果,并将贝叶斯方法嵌入到GERT网络方法中,由两者来联合展示易腐食品质量演变的动态性和随机性。算例结果表明本文模型的优势在于:不仅可对易腐食品生产质量和成本进行权衡分析,还可以从中寻找出易腐食品生产过程的关键环节。

本文的决策优化模型仍较理想化,现实决策时决策者面对的问题更为复杂。有待进一步扩展的方向包括:研究更为复杂的易腐食品生产过程质量控制问题,从长期的角度研究易腐食品质量改进效果对成本控制的影响等。