成本分担机制下共享供应链产品质量水平与及时交货水平最优激励策略

徐 琪 郭丽晶

(东华大学 旭日工商管理学院, 上海 200051)

0 引言

近年来,分享经济领域持续拓展,正在从消费环节进入生产环节,并延伸到供应链层面,从而涌现很多共享平台,提供供需资源的匹配。由于零售商(如设计师、品牌商、淘宝店主)的订货存货能力大都较低,小批量订货为主。但传统加工生产行业由于成本等因素很少有工厂愿意接小订单。随着共享经济的发展,通过共享平台聚合海量工厂,帮助零售商解决找工厂难、小订单难、翻单备料难等问题,实现生产资源的共享。例如,阿里旗下的1688“淘工厂”平台,整合全国1.5万家服装工厂,通过一个订单多家工厂加工的在线协同,利用各工厂的空闲档期实现产能共享的定制化生产,实现了淡季不“淡”的盈利目标。此外,委托生产、激励策略等也在分享经济中得到实践应用。例如,国内一些自有品牌的零售商或者网络零售商生产能力较弱,会选择委托生产的方式,通过“淘工厂”平台来找到合适的工厂进行生产。雀巢作为家乐福的供货商,为了降低缺货率,更好地管理库存与生产,其和家乐福投入资金共同建置了一套库存管理系统。同时,家乐福作为零售商也对物流等方面进行激励。如此一来,半年后雀巢的产品到货率由原来的80%提升到了95%,使得热卖品缺货率大幅降低,库存天数、订单修改率也得到下降。因而,在共享供应链中,资源的有效匹配共享、平台或零售商对生产/供应商的有效激励,均能起到提高产品质量和及时交货率的作用。

随着共享经济的发展,共享供应链的运作也面临着一系列问题,如共享工厂产品的质量水平、及时交货水平等问题,特别是在销售热期,如“双十一”期间,共享工厂的及时交货率远没有达到需求方的要求,而如果一味要求及时交货率,又可能带来产品质量问题。因此如何解决产品质量和及时交货率的矛盾是共享供应链需要探讨的重要问题。

产品的质量水平与交货期相互影响,交货水平的提高会影响质量水平[1],而且两者较多的是动态关系,对此,学者们利用微分博弈等方法开展了较广泛的研究。如,洪江涛[2]等采用微分博弈的方法研究了两级供应链在四种质量管理博弈情形下的最优质量管理策略及最优利润。王艳[3]等人利用微分博弈模型得出双寡头厂商的单位产品质保服务投入越高、质保期越长,均衡价格越高等结论。Voros[4]建立了一个需求同时依赖于价格和质量的动态模型。研究得出质量可以通过对开发过程的投资来提高,并且积累的质量知识的价值可以被纳入到模型中。Chen[5]等人运用博弈论方法对投入能力约束对食品质量和质量调节的影响进行了理论分析,其研究结果表明,两种能力投入约束均导致产出水平、质量水平和消费者剩余水平降低,但价格水平提高。他们还发现在食品质量保障方案中,奖励比惩罚或罚款更有效。Cellini[6]等人应用微分博弈提出了一个关于价格和质量竞争的动态模型来分析竞争对于质量的影响,其研究结果表明,如果供应商采用闭环决策规则,竞争越激烈,质量会越高,但是质量仍比开环规则下的低。Heydari[7]等研究了由单一再制造商和单一回收商组成的两级逆向供应链,其存在回收产品质量和再制造能力的不确定性,为此文中开发了一个定制的收益共享契约,以实现参与者分担风险的双赢。

由于工厂投入的及时交货水平(即服务水平)对利润有影响,高服务水平需要承受利润损失,而采取动态定价和订购联合决策可以降低追求服务水平所带来的利润损失[8]。因而,如何优化产品的服务水平也是近年学界研究的热点。如,王大飞[9]等通过构建两个销售阶段的动态博弈模型,分析了产品服务系统价值、成本和服务价值占比对消费者策略行为的影响。田魏[10]等分析了由两个制造商和一个零售商组成的双渠道供应链中制造商服务努力与广告成本的分摊及服务竞争对各方利润的影响。Chang[11]等提出了一种面向服务的动态多级预测维护分组策略,构造了惩罚成本和分组服务成本,设计改进的k-means方法动态地将预测的最优服务分组。

上述文献大多研究了质量水平与价格、质量投资、竞争和契约的相互影响,以及服务水平对利润、对消费者策略和分担成本等的影响,但这些文献考虑的是质量水平或服务水平单方面对各因素的影响,而本文则主要研究在共享情形下,产品质量水平和及时交货水平两者相互影响及对其他变量的共同影响。现实中,通常如果工厂被要求提高质量水平,很有可能订单的及时交货水平会降低;反之,若大幅提高及时交货水平,则产品质量水平又很难得以保证。本文通过构造不同共享激励组合,研究如何使得产品质量水平不变的情况下提高及时交货水平,从而提高供应链整体利润,使得共享供应链共赢。

关于成本分担契约,彭鸿广[12]等提出了不对称信息下供应链成本分担激励契约,旨在为供应商的努力提供不同程度的激励。其分析表明,最优契约中供应商的成本分担系数皆随成本不确定性的增加而减少,采购方对供应商的固定支付皆随成本不确定性的增加而增加。李小美[13]等人考虑供需同时不确定条件,设计了回购和成本分担组合契约,以协调该供应链,实现供应链利润的任意分配。刘云志[14]等针对考虑损失规避型零售商与产品质量水平的二级供应链协调问题,构建了回购-质量成本分担契约下的供应链协调契约模型, 并且证明了该供应链协调契约模型的有效性。王磊[15]等人设计了 “基于生鲜农产品新鲜度的采购价”契约和 “批发价 +保鲜成本分担”契约两种促进供应商提高保鲜努力的激励机制。这两种机制均能提高供应商保鲜努力水平,并且在一定程度上实现供应链协调。王芹鹏[16]基于制造商的低碳声誉和零售商的促销都能增加产品的需求,比较了不合作、成本分担契约以及合作3个契约对供应链成员的影响,并得出供应链利润在合作下最优。

上述关于成本分担的文献中,讨论的较多的是通过成本分担契约与其他种契约的比较而进行契约的选择。本文的成本分担机制,是通过探讨不同激励强度的成本分担组合,研究哪种激励组合下的成本分担契约更有效。

综上所述,上述相关文献对于供应链的质量管理、服务水平及成本分担契约已有较深入的研究,但是鲜有文献研究关于共享供应链下产品质量水平和及时交货水平的联合决策。故本文以共享平台为供需双方匹配订货和生产资源为背景,利用微分博弈模型,对于一个由工厂、共享平台和零售商组成的三级共享供应链,研究动态需求下,平台和零售商的成本分担激励组合决策,以在保证工厂产品质量水平的前提下,提高及时交货水平,从而促使共享供应链各成员通过激励机制,共享供需资源,提升工厂的生产资源的利用率和及时交货率,减小零售商产品或积压或缺货问题,实现共享供应链各方双赢。

1 模型描述与构建

1.1 假设与符号说明

对于一个由零售商(R)、共享平台(P)和签约的工厂(M)组成的共享供应链,考虑质量水平、交货水平,以及需求动态变化的情形,零售商通过共享平台提交订单,共享平台为其匹配合作签约的工厂进行产品的生产。工厂决定产品的质量投入努力和及时交货投入努力,并按平台收费模式付佣金给平台;平台为了提高工厂的交货水平,对工厂的及时交货所投入的成本给予一定的补贴,以激励工厂的交货投入努力;而对零售商而言,为了吸引更多的零售商利用平台进行订货,平台并不收取零售商的佣金。零售商采取动态定价策略,同时,一定条件下也分担工厂的产品质量的投入成本和及时交货率的投入成本。我们对平台只分担交货投入成本和零售商只分担质量投入成本的分担机制称为弱激励,而对零售商两者投入成本均分担,但平台仍只分担交货成本的分担机制称为强激励。这样,通过共享平台及时交货补贴激励和交货与质量投入分担机制,工厂、共享平台和零售商均可从资源共享中获得更多的收益,实现共享共赢的目的。

假设1工厂对产品的质量投入努力(研究人员、新技术、新设备等)将提高产品的质量水平。随着时间的推移,由于设备的老化、技术的落后等因素,若无持续的投入,产品质量水平存在衰减的状况。假设产品质量水平变化的状态方程为:

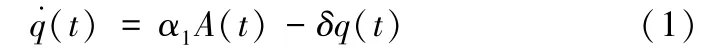
其中,表示t时刻产品的质量水平,初始质量水平q(0)=q0;A(t)为t时刻工厂的质量投入努力,α1＞0为工厂产品质量投入努力敏感系数,表示其质量投入对产品质量水平的影响程度;δ＞0为产品质量水平的衰减率。

假设2生产忙期,工厂往往由于忙于赶工而忽略产品质量[1],产品的及时交货水平(即准时交货率)和质量水平有一定的相关性。假设工厂的及时交货水平不仅与工厂的交货投入努力(用于增加工人、更新设备等)有关,还与产品的质量存在一定的负相关关系。则及时交货水平随时间的变化的状态方程可表示为:

其中,̇s(t)表示t时刻的及时交货水平,初始交货水平s(0)=s0;B(t)为t时刻工厂的及时交货投入努力,α2＞0为工厂及时交货投入努力敏感系数,表示及时交货投入努力对及时交货水平的影响程度;μ＞0为产品的质量水平对及时交货水平的影响程度;γ＞0为及时交货投入水平的衰减率,可由热销期、换季期或大型促销期间订单堆积而导致。

假设3通常零售商更倾向于寻找交货及时且产品质量高的共享平台下订单,为此参考Ouardigh[18]等将市场需求影响因素分为价格因素和非价格因素,且两因素可通过分离相乘的形式对市场需求产生影响的思路,假设产品的市场需求函数为:

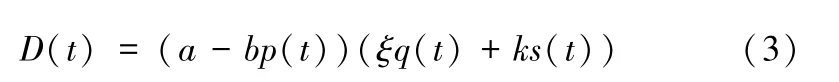
其中,p(t)为t时刻产品的零售价;ξ＞0,k＞0分别为消费者对产品质量水平和及时交货水平的敏感系数;b＞0表示消费者对价格的敏感系数,a＞0为市场规模,且a-bp(t)≥0。该需求函数说明市场需求受产品质量水平和及时交货水平的正影响,受价格的负影响(Dq＞0,Ds＞0,DP＜0)。产品质量水平和及时交货水平的增加会降低零售价对市场需求的负影响(Dpq=-ξb＜0,Dps=-bk＜0)。也就是说,随着产品质量水平和及时交货水平的提升,消费者对于该类产品的价格敏感度降低。其中Dq表示的是需求函数D(t)对q求一阶导,以此类推,Ds,Dp分别表示需求D对s,p求一阶导。Dpq表示需求函数D(t)先对p求一阶导,再对q求二阶导,Dps同理。

假设4质量水平和及时交货水平分别为质量投入努力和及时交货投入成本的凸函数:

其中,CMq(t)为t时刻工厂的产品质量投入成本,CMs(t)为t时刻工厂的交货投入成本;k1＞0,k2＞0分别表示工厂产品质量投入努力和交货投入的成本系数。

假设5假设工厂和零售商的基于完全信息的理性决策,不计供应链存货成本和缺货成本。工厂、平台、零售商有着相同的正贴现率。工厂产品的批发价为w(w＞0)。

以下是本文的关键符号和解释说明。

表1 符号及其解释说明Table 1Notations and explanations

1.2 模型构建与分析

1.2.1 共享平台和零售商弱激励下的投入努力和成本分担模型

弱激励成本分担是指平台只分担工厂及时交货努力的投入成本,而不分担产品质量投入的成本;零售商只分担工厂产品质量努力投入成本,不分担及时交货投入的成本。据了解,阿里的淘工厂平台关注于提高及时交货率,以吸引更多的零售商通过平台下单订货,因此平台对工厂实施及时交货努力的激励策略。

在此情形下,为吸引更多有资质的生产工厂和零售商加入平台,假设共享平台对每笔成交的订单向工厂收取佣金,比例为β,同时为工厂分担λ比例的及时交货的投入成本,以提高整个供应链的交货水平;零售商为提高消费者满意程度,也愿意为工厂分担一定比例的产品质量的投入成本,以提高产品的质量水平。在该共享供应链中,各成员的决策顺序为:首先零售商和平台同时决策他们各自最优的成本分担比例τ,λ,以及零售价p,接着工厂根据两类成本分担比例再分别决策其最优的质量水平投入和交货水平的投入(A,B)。

根据上述分析,工厂、平台和零售商的长期利润可分别表示为:

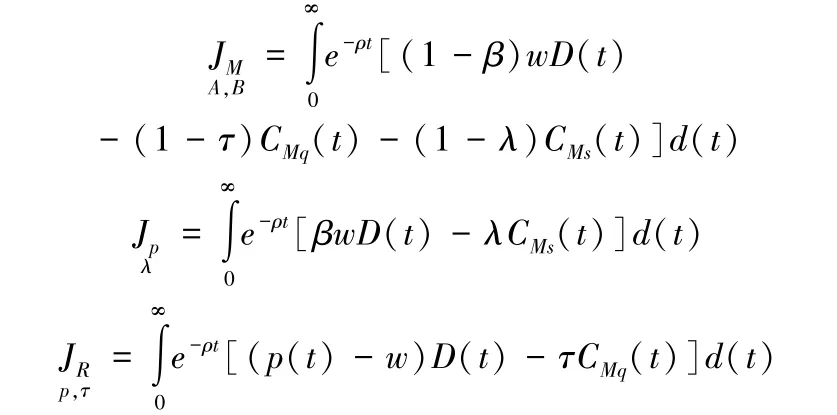
为方便书写,下文将不再列出时间t。

根据上述利润模型,我们采用逆向归纳法和最优控制理论对工厂的最优质量投入努力和及时交货水平投入努力,以及零售商和平台的成本分担比例进行求解分析,并由此可得到定理1。

定理1成本分担弱激励机制下,共享供应链中,工厂的最优产品质量投入努力、交货水平投入努力,零售商对工厂的质量投入成本的最优分担比例、最优零售价,以及平台对工厂的交货投入成本的最优分担比例分别如下:

证明:

记t时刻后工厂长期利润的最优函数为

根据最优控制理论,VM(q,s)对任意q＞0,s＞0都满足哈密顿-雅可比-贝尔曼方程(Hamilton-Jacobi-Bellman-HJB)方程:

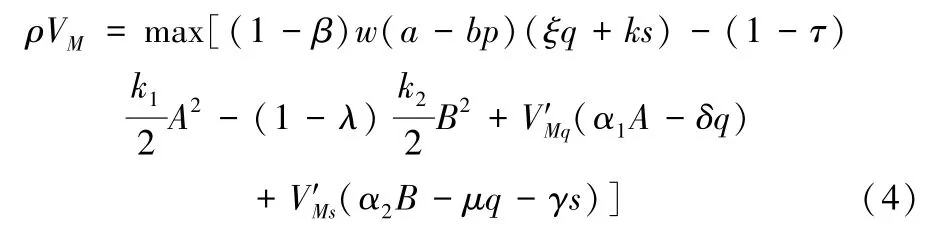
对(4)式分别关于工厂质量水平和交货水平投入求一阶偏导,并令其为0,可得:

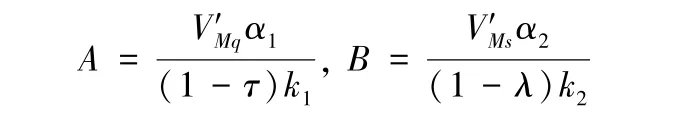
根据最优控制理论,Vp(q,s),VR(q,s)对任意λ＞0,τ＞0,p＞0都满足HJB方程:

将上述得到的工厂质量和交货率投入努力A和B代入式(5)、式(6),分别关于λ,τ,p求一阶偏导,并分别令其等于0,可得:

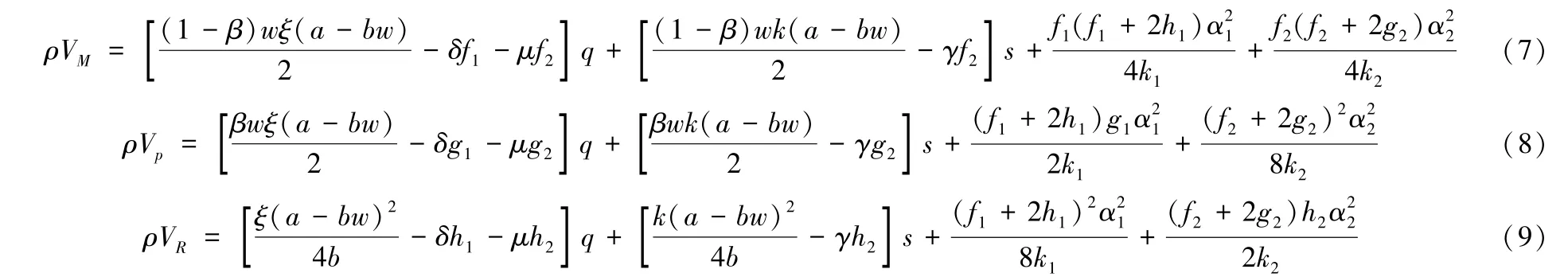
将λ,p,τ回代入工厂质量和交货率投入努力A和B表达式,则有:

根据式(4)-(6),假设最优价值函数VM(q,s),Vp(q,s),VR(q,s)关于q,s的线性解析式分别为:其中f1,f2,g1,g2,h1,h2为常数。 将VM,Vp,VR对q,s的一阶偏导以及A,B,λ,τ,p代入(4)-(6),可得:

由式(7)-(9)可解得:

最后,回代f1,f2,g1,g2,h1,h2,即得到定理1中的A∗,B∗,λ∗,τ∗,以及最优值函数VM,Vp,VR:

证毕。

从定理1我们可看到,若想λ∗＞0,必须3β-1＞0,即β=1/3是平台对工厂及时交货投入进行补贴的临界条件,大于该临界值,意味着平台对工厂及时交货投入给予一定比例的补贴;而当3β-1＜0时,λ∗＜0,此时意味着平台给予工厂的补贴为负,实际上就是工厂不仅要承担自身的投入成本,还要支付给平台一定比例的费用成本,这情形不符合本文中的激励机制,故下文仅考虑λ∗＞0,即β＞1/3的情况。

由定理1得,在成本分担机制下,工厂的最优质量投入努力与市场质量敏感程度正相关,与交货水平因子负相关,与质量成本参数,质量衰退率和时间贴现因子负相关;最优交货水平与市场交货敏感程度正相关,与交货水平成本参数,交货水平衰退率和贴现因子负相关。当w∈(0,a/(2b))时,产品批发价正向影响工厂的质量投入努力和交货投入努力(∂A/∂w＞0,∂B/∂w＞0);当时,产品批发价正向影响工厂的质量投入努力,负向影响其交货投入努力(∂A/∂w＞0,∂B/∂w＜0);当时,产品批发价负向影响工厂的质量投入努力,负向影响其交货投入努力(∂A/∂w＜0,∂B/∂w＜0)。当w=a/(2b)时,供应链及时交货投入努力达到最大值;当w=a(1+β)/(2bβ)时,产品质量投入努力达到最大值。而且,市场质量偏好以及产品质量水平对交货水平的边际贡献率均影响工厂的质量投入努力,但不影响其交货投入努力。平台对工厂的交货成本的分担比例只受到佣金的影响。此外,零售商的零售价格与批发价,市场规模和价格敏感系数相关,其对工厂的质量成本的分担比例受批发价、市场规模和价格敏感系数影响,随着批发价上升,零售商愿意为工厂分担的质量投入成本比例减少(∂τ/∂w＜0)。

进一步,将上述最优策略代入状态方程(1)和(2)中,可得工厂的产品质量水平和及时交货水平路径轨迹的微分方程:

求解上述两微分方程即可得如下定理2。

定理2成本分担弱激励机制下,共享供应链产品质量水平和及时交货水平的最优轨迹分别为

其中,

q∞,s∞分别为成本分担模型下产品质量水平和及时交货水平的稳定值(与时间无关的量)。

从定理2的式(10)我们可看到,由于q0是常数,故质量水平和及时交货水平的稳定值q∞,s∞是唯一影响最优质量水平轨迹和最优及时交货水平轨迹的变量。因而,分析稳定值的特点可间接得出质量水平和交货水平的特点。

共享平台和零售商在弱激励成本分担机制下,共享供应链中工厂的质量水平和及时交货水平的稳定值与市场质量和交货敏感程度正相关,与质量水平对交货水平的边际贡献、成本参数、两者衰退率和时间贴现因子负相关。特别是当时,产品批发价正向影响产品质量水平和交货水平的稳定值(∂q∞/∂w＞0,∂s∞/∂w＞0);当时,产品批发价正向影响产品质量水平的稳定值,负向影响其交货水平的稳定值(∂q∞/∂w＞0,∂s∞/∂w＜0);当时,产品批发价负向影响工厂产品质量水平和其交货水平的稳定值(∂q∞/∂w＜0,∂s∞/∂w＜0)。其中(-kμ+γξ+ξρ)。因此,当时,工厂产品质量水平的稳定值达到最大值,这与定理1得出的结论一样;当w=时,工厂交货水平的稳定值达到最大,这与定理1得出的结论中的临界点不同,因为及时交货水平受工厂交货投入努力及质量水平的影响。

另外,在成本分担机制下,产品质量水平的轨迹是单调的,而交货水平轨迹呈多变性。从式(10)可以看出:当q0＜q∞时,质量水平的轨迹随着时间单调递增;当q0＞q∞时,质量水平的轨迹随着时间单调递减;当q0=q∞时,质量水平为常数。然而,由于供应链交货水平受到工厂交货投入努力与质量水平的联合影响,其轨迹呈多样性变化。结合最优策略和最优状态轨迹,可以得出共享平台和零售商在成本分担弱激励下共享供应链的整体利润为:

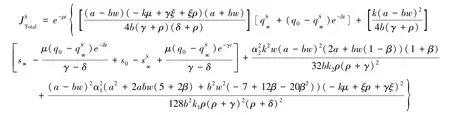
1.2.2 平台和零售商强激励下的投入努力和成本分担模型

平台与零售商强激励的成本分担机制是指零售商既分担工厂质量努力投入成本,同时也分担工厂的及时交货努力投入成本;而平台则与弱激励情形下的分担机制相同,即只分担工厂及时交货的投入成本。这种情况通常较多的出现于销售旺季,此时工厂因产能、提前期等因素的影响,其及时交货率难以满足零售商要求。为了防止工厂因赶工而降低产品质量的情况发生,零售商愿意对工厂的质量投入和交货投入成本同时给予补贴,以进一步激励工厂,使得产品质量保证的前提下,交货水平也提高,从而避免因交货不及时带来的缺货损失。也就是说,在该情形下,平台和零售商都想进一步提高及时交货率,从而促进整个供应链利润更优。现实中,很多生鲜超市、便利店等对产品的及时到货率很看重,例如,日本大型连锁便利店“7-11”的新鲜食品占其销售额很大一部分。其中,便当、沙拉等新鲜食品都需当天送达以进行售卖,此时供应商的食品是否准时到货将直接影响该门店销售额。为提高及时交货率确保在就餐时间点前能送达,“7-11”投资建立了配送中心,所有食品供应商统一将食品运到配送中心,然后配送中心将所有来自不同供应商的产品进行重组运到各连锁店。“7-11”公司这一战略补贴不仅为供应商减少了派送货物的时间,提高产品到货率,还能合理地管理产品库存。因此在本文中,进一步研究平台和零售商都对工厂的及时交货努力进行激励时供应链各方的最优投入,使得共享供应链整体收益最优。

强激励成本分担机制下,共享供应链的决策顺序为:平台和零售商首先同时决策他们各自关于工厂的质量水平和交货水平最优分担比例λ,(v,τ)及零售商价格p,接着工厂根据分担比例再分别决策其最优的质量投入努力和交货投入努力(A,B)。由此,三方利润函数可分别表示如下:

对上述利润函数,采用逆向归纳法和最优控制理论进行求解,可得定理3。

定理3在平台和零售商强激励成本分担机制下,工厂最优的质量投入努力和及时交货投入努力、零售商分担工厂的最优质量成本和及时交货成本的最优比例、最优零售价格,以及平台分担的工厂及时交货投入成本的最优比例分别如下:

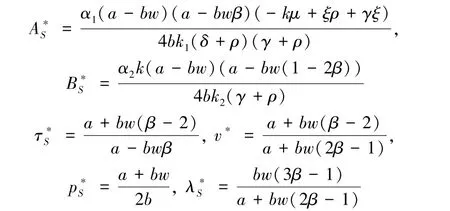
同理,由定理3知,只有当3β-1＞0时,λ∗＞0,由于本文仅讨论激励机制下的最优解,故3β-1＜0时的情况不考虑。

从定理3我们可看到:在强激励成本分担模型下,对工厂而言,工厂的最优质量投入努力与市场质量敏感程度正相关,与市场交货水平敏感程度负相关,与质量成本参数、质量衰退率和贴现因子负相关;最优交货投入努力与市场交货敏感程度正相关,与交货水平成本参数和衰退率、贴现因子负相关。

对零售商而言,零售商的零售价与批发价,市场规模和价格敏感系数相关。随着批发价上升,零售商愿意为工厂分担的质量投入成本比例减少(∂τ/∂w＜0),为工厂分担的交货投入成本比例减少(∂v/∂w＜0),且零售商将通过提高零售价格来降低因批发成本增加和分担比例增加而带来的损失(∂p/∂w＞0)。

进一步,将定理3中的最优决策变量代入状态方程(1)(2)中,得:

求解上述微分方程即可得如下定理4。

定理4强激励成本分担机制下,共享供应链产品质量水平和及时交货水平的最优轨迹分别为:

其中,

由定理4可看出:在强激励成本分担机制下,共享供应链的产品质量水平和及时交货水平受其稳定值的影响,两者的稳定值与市场质量和交货敏感程度正相关,与质量水平对交货水平的边际贡献负相关,与质量和交货水平的成本参数,衰退率和贴现因子负相关。同时,当

时,产品批发价负向影响供应链质量水平的稳定值,正向影响其及时交货水平的稳定值(∂q∞/∂w＞0,∂s∞/∂w＞0);当w∈时,产品批发价负向影响供应链质量水平的稳定值,负向影响其交货水平的稳定值时,产品批发价负向影响供应链质量水平的稳定值,负向影响其交货水平的稳定值(∂q∞/∂w＜0,∂s∞/∂w＜0)。其中,m1=因此当w=时,供应链质量水平的稳定值达到最大值,这与定理3得出的结果一样;当时,供应链及时交货水平的稳定值达到最大。

结合最优策略和状态轨迹,可以得出强激励成本分担机制下供应链整体利润为:

1.3 比较分析

基于上述研究,本小节比较弱激励和强激励成本分担机制下共享供应链中的最优零售价格、工厂的产品质量最优投入努力、及时交货最优投入努力的差值,进而判断共享供应链应采取哪种激励机制使得整体利润最优,可有:

从中可发现,强激励和弱激励成本分担机制下共享供应链产品的零售价和产品质量投入努力均一致,但及时交货努力不确定。由于a-bp≥0,p＞w,故(a-bw)＞0。当a/b(2-β)≤w≤a/b时,ΔB＞0,即此时弱激励成本分担机制及时交货投入努力更佳,当w＜a/b(2-β)||w＞a/b时,ΔB＜0,此时强激励成本分担机制及时交货投入努力更佳。因而,根据目标市场产品的成本区间,选择不同激励的成本分担机制,通过共享供应链的资源共享,在一定的激励机制下,即使在热销期产品的及时交货率也能够得到保障,同时产品质量不受影响。

进一步,我们比较弱激励和强激励下平台分担比例、零售商分担比例、产品质量水平、及时交货水平及质量和及时交货的稳定值的差值,如下所示。由于分担比例λ≥0,故3β-1≥0。

根据上述假设,可以直观地看出:零售商对工厂产品质量成本的分担比例在强激励下与弱激励下相等,即零售商不会因为自身分担了工厂的及时交货成本而减少质量成本的分担比例;强激励下平台对及时交货成本的分担比例小于弱激励下的,也就是说,强激励下零售商对于及时交货成本的分担,降低了平台的分担负担;强激励下的产品质量水平、质量水平的稳定值与弱激励下一致,但及时交货水平、及时交货的稳定值则与及时交货投入努力一样,与批发价有一定的关系。

两种激励组合下共享供应链整体供应链利润之差为:

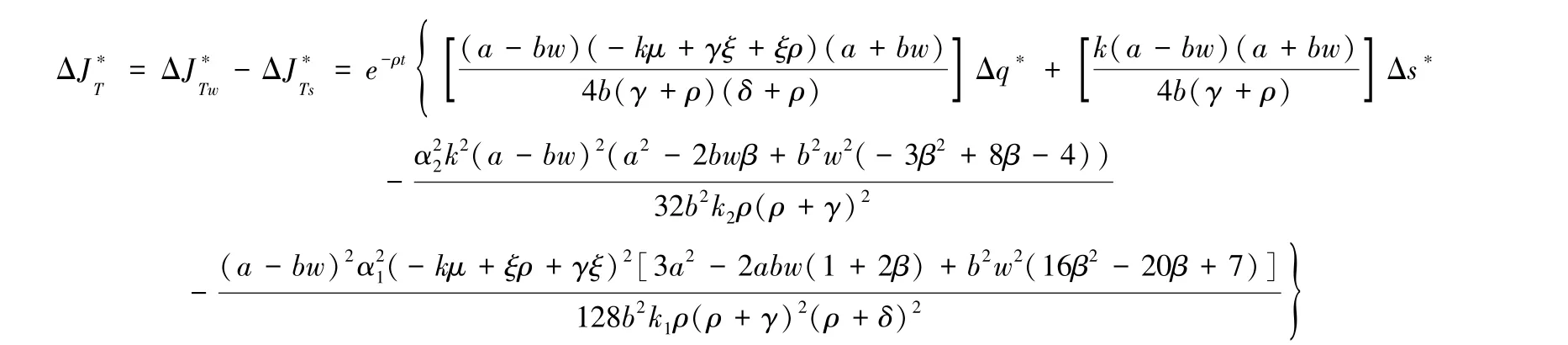
由于上式无法直观地比较出两种激励制度下利润的大小,故下面借助数值分析来观察两种激励策略的利润情况。

从数值分析可知,当0≤w≤a/b时,有,此时弱激励下共享供应链系统的利润小于强激励下的,零售商和平台应该选择强激励成本分担机制;反之,应该选择弱激励下的成本分担机制。

综上所述,共享供应链弱激励成本分担机制和强激励的成本分担机制下,产品价格、零售商对产品质量成本的分担比例以及工厂对产品质量的投入努力均相同。零售商对工厂及时交货投入成本的分担机制能够降低平台成本分担的压力,激励平台不断提升供需资源的匹配效率,提高及时交货水平,达到共享资源充分利用的目的。

但是,供应链应根据目标市场产品的成本定位,选择相应激励的成本分担机制,决策最优投入努力和分担比例。当0≤w≤a/b(2-β)时,强激励成本分担机制可保证质量水平不变的前提下,提高及时交货水平,且此时共享供应链的整体利润较高;当a/b(2-β)＜w≤a/b时,虽然此时弱激励成本分担机制及时交货水平较高,但是供应链整体利润低于强激励机制,因此供应链仍需采用强激励成本分担机制;当w＞a/b时,虽然强激励下的及时交货水平较高,但整体利润却降低,故此时供应链应选择弱激励成本分担机制。

2 数值分析

为了更直观地分析不同成本分担激励机制下共享供应链的最优均衡策略、质量水平和交货水平状态变量轨迹以及整体利润等,本节对外生变量赋值进行数值分析。借鉴游达明[17]等的研究成果,参数的设置如下表所示:

表2 参数赋值Table 2Parameter assignment

由表3可看出,在基准参数下,强激励成本分担机制在保证质量水平不变的前提下,大大提高了及时交货水平且共享供应链整体利润也提高了很多。下面是基准参数下,最优产品质量水平和及时交货水平的轨迹,如图1所示。

表3 不同激励下的最优策略Table 3Optimal strategies under different incentives

图1 基准参数下状态变量的最优轨迹Figure 1Optimal trajectories of state variables under reference parameters

从图1可知,两种成本分担激励机制下的产品质量水平一致,且质量水平随着时间递增直到维持某一水平。对于及时交货水平来说,由于受到质量水平和衰退率的影响,弱激励下的及时交货水平轨迹随时间先递增再小幅衰减直至稳定在一定水平,而强激励下交货水平随时间递增直到维持在某一水平;强激励下及时交货水平始终远远高于弱激励下的及时交货水平。

综上,在基准参数下,强激励成本分担机制下的共享供应链整体利润大于弱激励成本分担机制下的利润,且前者在保证工厂质量水平不变的前提下,大大提高了及时交货水平。因此,共享供应链此时会选择强激励的成本分担机制。

平台的佣金率对各分担比例有重要影响。保持其他参数不变,图2显示了佣金率的变化对供应链整体利润、零售商对工厂产品质量投入成本的分担比例τ、平台对工厂及时交货生产成本分担比例λ和强激励下零售商对工厂及时交货投入成本的分担比例v的影响。显然,无论佣金率如何变化,强激励下供应链整体利润始终高于弱激励。对于λ来说,随着佣金率的增加,强激励下平台的分担比例先大于弱激励,再小于弱激励。对于τ和v来说,两者都随着佣金率的增加而增加。故而,在现实生活中,平台可以通过控制其对工厂的佣金率来决策其分担比例,使得自身利润最优并同时激励工厂提升交货率。

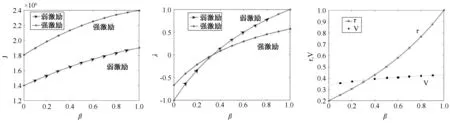
图2 佣金率对利润、分担比例的影响Figure 2The impact of commission rate on profit and sharing proportion

保持其他参数不变,图3显示了批发价对质量水平、及时交货水平和利润的影响。对于及时交货水平来说,当批发价w≤50||w≥80时,强激励下的及时交货水平始终略高于弱激励下的。从利润曲线可看出,当0≤w≤50时,强激励下的供应链整体利润大于弱激励下的利润,故此时供应链成员会选择弱激励的成本分担契约,反之若则选择弱激励成本分担契约。因此,现实中,针对批发价较低的产品,采用强激励成本分担组合更能刺激供应链质量水平、及时交货水平和利润;而针对高端昂贵产品,采用弱激励成本分担组合则更有优势。

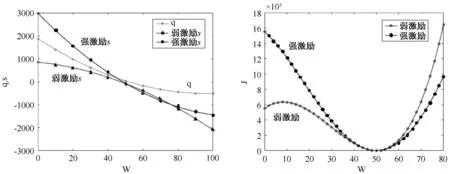
图3 批发价对相关变量的影响Figure 3The effect of wholesale prices on related variables

3 结论及结束语

本文针对共享平台激励问题,考虑产品质量水平和及时交货水平随时间动态变化,且相互影响的情形,采用分离相乘的方法,描述价格因素和非价格因素(产品质量水平和及时交货水平)对市场需求的动态影响,构建动态微分博弈模型和不同激励程度下的成本分担模型,研究共享供应链产品质量和及时交货水平的最优投入水平、定价和成本分担策略,并结合数值仿真,对相关参数进行了灵敏性分析。基于上述研究,可得出以下结论:

(1)弱激励和强激励的成本分担机制下,两者的产品零售价、产品质量水平以及零售商对工厂产品质量投入成本的分担比例都一样。但当批发价w＜a/b(2-β)||w＞a/b时,强激励策略中工厂在保证质量不变的前提下,及时交货水平及其稳定值都高于弱激励下的。另外,强激励下零售商对于工厂及时交货投入成本的额外分担会减轻平台对此成本分担的压力,从而使平台的分担比例降低。就质量水平而言,产品质量水平随时间单调递增后维持某一水平不变,在这种轨迹下供应链利润最优,也就是在现实市场中,工厂一开始先提高产品质量水平,后期只需维持该水平,供应链利润就可一直在较高水平。而及时交货水平随时间变化呈多样性,弱激励下,工厂一开始需小幅提高交货水平而后略微递减使其稳定在某一水平,在这种轨迹下供应链利润最优;强激励下,工厂需快速提升及时交货水平而后稳定至某一水平,此时整体利润在这种轨迹下达到最优。

(2)当0≤w≤a/b时,强激励成本分担机制下供应链整体利润大于弱激励成本分担机制。此时,零售商既分担工厂的质量投入成本又分担工厂的交货投入成本。共享供应链会选择强激励成本分担机制来更好地促进供应链提升及时交货水平,达到供应链共赢。

(3)平台对工厂的佣金率的提高能增加平台和零售商对工厂生产成本的分担比例和供应链整体利润。

(4)批发价的变化对状态变量和整体利润有重要影响。当批发价较小时,强激励成本分担机制下及时交货水平更好,供应链利润较优,否则弱激励成本分担机制下两者较好。

综上所述,强激励成本分担机制和弱激励成本分担机制各有优劣。当目标市场的产品为中低成本产品(如服装、配饰等)时,零售商对工厂交货水平的进一步激励手段能显著提高订单的及时交货水平,且供应链整体利润大幅提升。故此时强激励成本分担机制能更好地促进供应链各方共赢。在强激励成本分担机制下,工厂一开始需快速提升产品质量水平和及时交货水平而后使其稳定至一定水平即可达到最优状态。目前国内一些自有品牌的零售商或者网络零售商由于生产能力较弱,会选择委托生产的方式,通过阿里巴巴的1688下的“淘工厂”平台来找到合适的工厂进行生产。一方面平台为了提高交货水平,它会将聚集的订单按工厂的忙闲来分配,既能高效的提高交货率,又能使得工厂提高开几率,减少因空闲造成的资源浪费。另一方面,由于工厂的机会主义行为会给自有品牌商品质量带来隐患,故零售商会采取成本分担等手段来激励工厂提升产品质量。当目标市场产品是高成本产品(如电脑、手机等)时,零售商对及时交货水平的激励手段反而会降低整体利润,适得其反。这是因为高成本产品的生产周期本身就长,且生产过程更为周密复杂,生产线的交货水平相对稳定,故需投入更大的努力才能提高及时交货水平,而这会导致交货投入成本陡增,降低利润。故在此时,弱激励成本分担机制更有优势,既能保证质量和交货水平,又能提高供应链整体利润。在弱激励成本分担机制下,工厂需快速提高产品质量水平而后维持不变,而对于交货水平,可采取先小幅提高再适当回落的方法使得整体利润最佳。

本文关于共享供应链的产品质量水平和及时交货水平的研究还存在一些局限性,未来可从以下两方面进行拓展。其一是共享供应链中共享平台(以“淘工厂”为例)的订单分配问题以及订单分配对产品质量和及时交货的影响问题;其二是对于佣金小于一定值时造成的平台分担比例小于零的工厂补贴情形可进一步展开讨论。