等腰三角形中的分类讨论思想

蔡春儒

等腰三角形是生活中最为常见的三角形之一，它的应用非常广泛，因此也将它作为学习和考试的一个重点，但它具有其独特的特点，它在边和角上都有一定的特殊性，比如：等腰三角形看上去舒适感非常强，原因是它有两条边一样长，并且两个角的度数是一样大的。我们在做题的过程中遇到的有关等腰三角形的题目大多分为三方面：边长、角度与图形面积。虽然等腰三角形的特征非常简单易懂，但是所涉及到题目的却是非常多、非常广的，而且难度也是不一样的。在日常学习中可以发现，虽然等腰三角形的知识不难，但是我们在解决有关等腰三角形方面的问题时，却很难拿到满分，很多时候我们在做题时都存在打不开思维，局限于一个特征，没有进行关联。其实纵观数学科目上的问题可以发现，不仅仅是等腰三角形，其他类型的题目也是具有非常多的解题方法，而且只要打开思维，都会豁然开朗，眼前一亮。

一、分类讨论思想的重要性

首先，分类讨论思想在数学解题过程中是非常重要的，数学题目的变换是多样的，但是解题的思想是不变的，通过分类讨论思想来进行解题，有很大的便捷性。利用分类讨论思想，可以促使我们的解题思维具有非常大的提升，数学知识难易不一，而且很多知识都是比较抽象的，我们在做数学题时只有对题目做出有效的把握，才可以提高解答数学题目的准确性和正确率。

其次，我们通过分类讨论思想还可以提高数学知识与生活实际的联系。平时的学习过程中我们对数学知识点的学习仅仅停留在表面，而不是更加深入的联系，一旦生活中出现了相类似的情况是无法进行解决的。所以在学习数学过程中使用的分类讨论思想进一步将我们学习到的数学知识进行了运用，把我们学到的数学知识正确的运用到生活中去，提升了我们的思维运用能力，同时还让我们的思维更加严谨。

最后，在等腰三角形的解题中广泛应用有关分类讨论的思想，数学知识广阔无边，知识点有很多，比如在解决函数问题时可以运用分类讨论思想，在概率题中可以使用分类讨论思想，同样在将来进入高中后学到的数列也可以使用分类讨论思想。分类讨论思想的运用是非常广泛的，而且在进行数学解题的过程中，逐步提升我们对生活中真实问题的解决能力，通过做题让我们更加善于对分类思想的应用，并将这种思想迁移到其它知识点的学习中去，逐步将这种思考问题的方式运用到其它问题的解决中去。

二、等腰三角形中对分类讨论思想的应用

在涉及等腰三角形的具体问题时，由于等腰三角形需要确定一个顶角，才能将这个三角形的边和角确定，所涉及到的题目也是多种多样的，而且时常会与函数和方程等多个知识点进行关联，题型多样。所以在涉及等腰三角形的题目时，首先需要我们牢牢掌握住等腰三角形的特征和等腰三角形的相关基础概念，并进行思维发散，打开思维，不要局限。另外还要重视分类讨论思想在等腰三角形中的渗透和运用，将知识进行融合和创新。

（一）等腰三角形中“边”的分类讨论

在日常的等腰三角形的练习中我们可以发现很多看起来非常简单，而且题目也非常容易理解的题，但是卻很容易失分。明明题目很清晰明了，没有拐弯抹角的题干，但是在做题中却很难得道满分。但是当我们仔细分析题型就可以发现，很多题目中都会有分类思想的出现，我们常常只是站在一个角度去思考问题，从而忽略了换个角度后的答案。比如题目一：拿到一个等腰的三角形模型，通过测量，其中一条边长为8cm，一条边长为5cm，问这个三角形模型的周长是多少厘米？

这个题极其简短，而且很容易读懂，但是这也是我们在日常练习中比较容易丢分的题，这个题需要我们考虑到，题中并没有明确的指出这两条边是哪的边，所以有可能是底边，也有可能是腰，因此本题的解题思路就要分为两种：当8cm作为腰时，当5cm作为底边的情况，第二种情况是8cm作为底边，5cm作为腰的情况，所以本题的答案是21cm和18cm。

但是，并不是所有的涉及到边的题型都是需要考虑两种情况，还要考虑本题是否符合三角形的三边关系。比如例题二：拿到一个等腰的三角形模型，有一条边是长3cm有一条边是6cm，问这个三角形模型的周长是多少厘米？

三角形的三边关系是“三角形的任意两边之和大于第三边”，通过这个特征我们便可以知晓，只有底边长为3cm才能构成三角形。如果底边为6cm时，不符和三角形的三边关系定理。因此，本题的答案是15cm，只有一个答案。由此可以看出，在有关等腰三角形的题型中对分类讨论的思想的使用非常重要，可以帮助我们分析题型。

（二）等腰三角形中“角”的分类讨论

在等腰三角形的“角”的相关题型中也会用到分类讨论的思想，比如题目一：拿到一个等腰的三角形模型其外角为130°，那么这个等腰的三角形模型的底角为多少度？

题目中已知的信息是外角是130°，则可以计算出其相邻的内角就是50°，通过分类讨论，我们并不知道这个50°是哪个角，所以分类一，当50°是底角时，分类二，当50°是顶角时，由此得出答案也是有两个。

比如题目二：在等腰三角形中，∠ A的度数为X，∠ B的度数是X+60°，那么X是多少度？

上题的条件中已知三角形是等腰三角形，但是可以发现题中并没有明确指出相等的边是哪两条，因此要进行分类讨论，当∠ A是顶角时，此时的方程可以列为 X+2（X+60°）=180°，而后解得X=20°;当∠ B 为顶角时，此时的方程为X+X+X+60°=180°，解得X=40°，因此，本题的答案是20°或40°.

比如题目三：一个等腰的三角形模型的内角是另一个内角的2倍，那么这个等腰的三角形模型的内角分别为多少度？

通过对上题的条件分析得出，本题中并没有对角做出具体的说明，所以本题依旧需要用分类讨论的思想来解决。首先，如果底角是顶角的2倍，此时需要设顶角为X，那么底角就是2X.所列方程为：2X+2X+X=180°，X=36°，2X=72°.那么此时等腰三角形的内角度数分别为：36°，72°，72°.第二，如果顶角是底角的2倍，此时设底角为X，顶角为2X.所列方程为：X+X+2X=180°，X=45°，2X=90°。所以顶角是底角的2倍这种分类时，此时，等腰三角形的三个内角度数分别为：45°，45°，90°.

（三）等腰三角形中“形”的分类讨论

在等腰三角形的角和边的题型中都运用到了分类讨论的思想，另外，还有更多的题型使用到了分类讨论思想。比如题目：拿到一个等腰的三角形模型中的一个腰上的高与另一个腰上的夹角是48°，那么这个等腰的三角形模型的底角为多少度？

这个题目的也是需要通过分类来完成，第一，当等腰三角形的模型是锐角的时候，一条高就是90°，顶角∠ A就是90°-48°=42°，那么此时的底角就是69°.如果三角形时是钝角三角形时，高在三角形的外部，此时顶角就是138°，底角为21°。所以可以看出，在等腰三角形的形中也会用到分类思想。

（四）等腰三角形中“线”的分类讨论

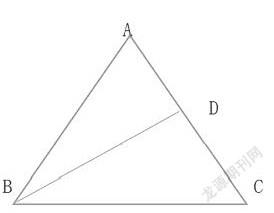
在等腰三角形中，由于腰上线的位置不同，所以也要运用分类讨论的思想进行解答。比如在题目：一个等腰的三角形模型任意一个腰上的中线把模型的周长分成了15厘米和18厘米，那么这个等腰的三角形模型的底长和腰长为多少度？

这个题中，需要对中线的情况进行分类，由上图可以看出边AB与边AC相等，BD是AC边上的中线，由此可以得出AD=CD，AB=2AD，题中的周长分别是15和18厘米，可以列式为：AB+AD=15，BC+CD=18，又因为AB=2AD，所以得出，AD=5，那么AB=10，BC=13;另一种情况是AB+AD=18，BC+CD=15，可求得AB=12，BC=9。

（五）等腰三角形在“坐标轴”中的分类讨论

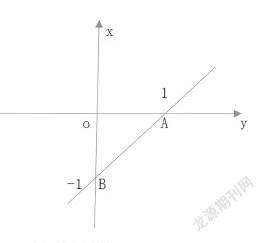
除了上述一些题型外，有时可以将一个等腰三角形放到坐标轴中去讨论。比如题目：下图中的坐标轴中，A的坐标是（1，0），B的坐标是（0，-1），在X轴上任意找一个点，让三角形ABC是一个等腰三角形，那么点C可以在哪里？

此时，就运用到了分类讨论思想，就是让点A，点B，点C分别都作为等腰三角形的三个顶点来进行分类，那么就会出现三种情况：第一，此时把A看做是三角形的顶点，则点C的坐标可以是（ 2  +1，0）、 （1-  2  ，0）.第二种情况，此时如果把点B看成是顶点的话，则点C的坐标是（-1，0）。第三种情况，此时如果点C是等腰三角形的顶点，则点C的坐标是（0，0）。

总之，分类讨论思想在解答的过程中的应用可以发现，它们在与“边”“角”“形”“线”“坐标系”的相关题目中，通过运用分类讨论思想让这类数学题更加清晰明了，等腰三角形中所运用的分类讨论思想让我们在解题过程中，思考的更加全面而谨慎。不单单是等腰三角形中可以使用到分类讨论思想，在其他类型的题目中同样适用，分类讨论可以帮助我们做题，让复杂的题目变得更加简单清晰，同时还能让我们做题的思路更加广阔，将题干中所涉及到的情况都考虑周全，不易丢分。数学中的题型多种多样，而且题目的数量又有很多，所以我们永远都有做不完的题，但是不管题目发生什么样的变化，其思想内涵和解题的思路是不变的，可以采用多種多样的方法，而分类讨论的方法将数学方法和数学问题进行了很好的融合，不管题目有多难，融合了几个知识点，依旧可以通过分类讨论来解决。

【本文系黑龙江省教育科学“十四五”规划2021年度教研专项重点课题《中小学生自主学习能力培养策略研究》（课题编号：JYB1421649）研究成果】

指导教师：张春明

（作者学校：齐齐哈尔市拜泉县国富镇中心学校九年二班，黑龙江  拜泉  164700）