关联图形 拨云见日——2021年宁波市数学中考第16题的解法与探究

陆丽丽

(镇海蛟川书院，浙江 宁波 315201)

1 原题呈现

例1如图1，在矩形ABCD中，点E在边AB上，△BEC与△FEC关于直线EC对称，点B的对称点F在边AD上，G为CD中点，联结BG分别与CE，CF交于点M，N.若BM=BE，MG=1，则BN的长为______，sin∠AFE的值为______.

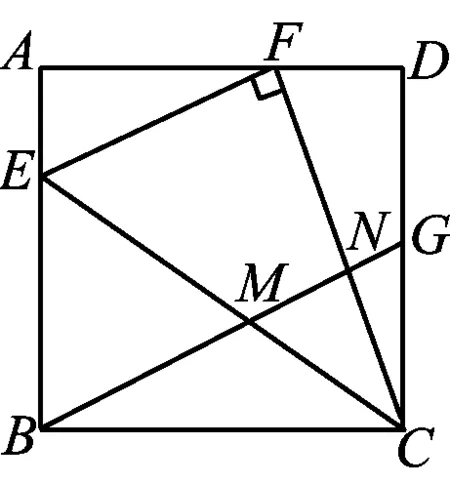
图1

(2021年浙江省宁波市数学中考试题第16题)

本题以矩形为背景，融入轴对称变换，考查特殊三角形、特殊平行四边形、勾股、全等、相似等核心知识，渗透方程、转化等数学思想方法，兼顾基础性和区分度.很多考生反映第一空是猜的，第二空太难，未知量太多，无从下手.本文抛开第一空，直接探讨第二空求“sin∠AFE”的值.

2 解法探究

学生基本能推得AB,CD的长.由BM=BE，可知

∠BEM=∠BME，

因为AB∥CD，所以

∠BEM=∠GCM.

又∠BME=∠GMC，从而

∠GCM=∠GMC，

于是

MG=GC=1.

由G为CD的中点，得

CD=AB=2.

目标∠AFE在Rt△AFE中，只要求出AE,EF的比值即可.但是△AFE的3条边和边AD都未知，且与已知量MG的关系不明确，这些导致学生的思维受阻，无从下手.观察条件“△BEC与△FEC关于直线EC对称且点F在边AD上”，由轴对称性得△BEC≌△FEC，进而得三角形对应边、对应角相等.如何运用此性质与其他条件关联并挖掘更深层次的结论是解决本题的关键.

视角1关联轴对称和等腰得平行.

如图2，由轴对称可知△BEC≌△FEC，即

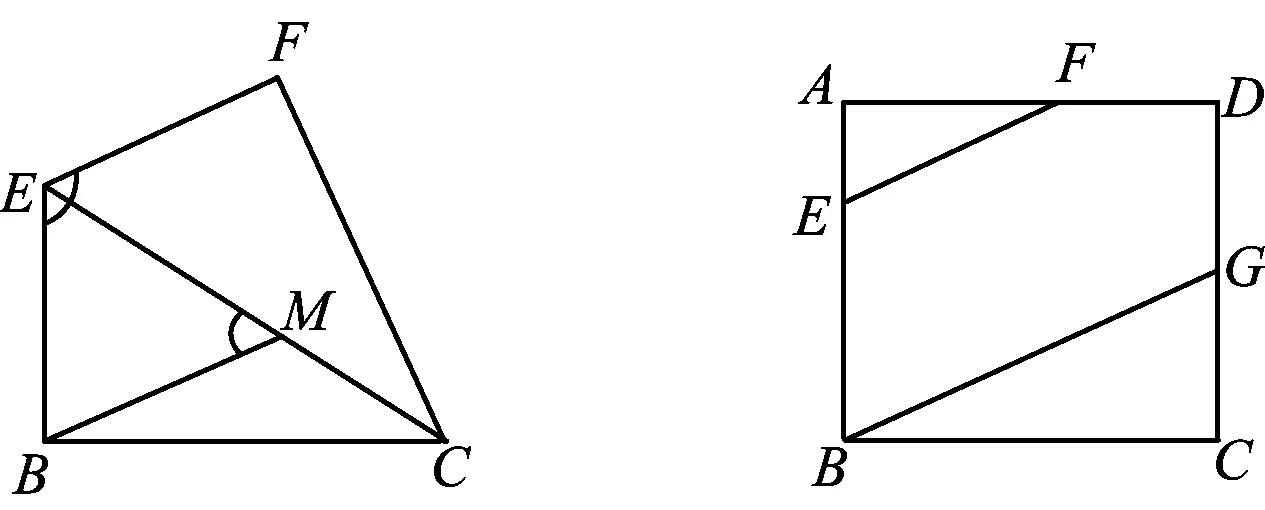
图2 图3

∠BEM=∠FEM.

因为BE=BM，所以

∠BEM=∠BME，

从而

∠FEM=∠BME，

于是

EF∥BM.

解法1(由平行找相似建立方程)如图3，由AD∥BC可证∠AFE=∠GBC，从而

Rt△AFE∽Rt△CBG,

于是

设BE=BM=EF=x，则

AE=2-x，BG=1+x，

得

解得

于是

解法2(由平行+倍长中线建立方程)由△BEC≌△FEC和BM=BE，得EF∥BM.如图4，分别延长AD,BG交于点P，由点G为CD的中点可知BP=2BG且△AFE∽△APB，从而

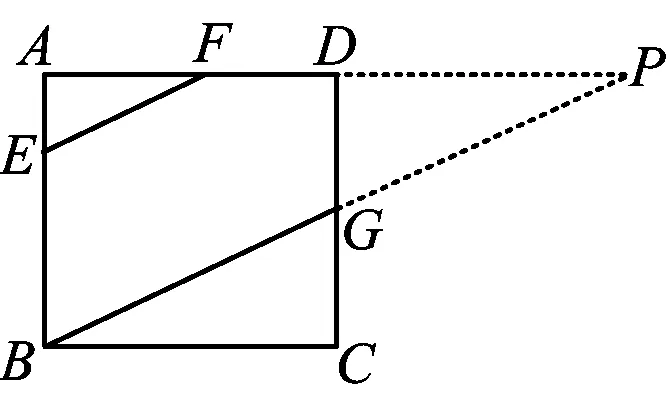
图4

于是

解得

故

解法3(由平行得垂直，构造全等和相似)由△BEC≌△FEC和BM=BE，得EF∥BM.如图5，因为∠EFC=90°，所以∠BNC=90°，又BC=FC，易证Rt△BNC≌Rt△CDF，得

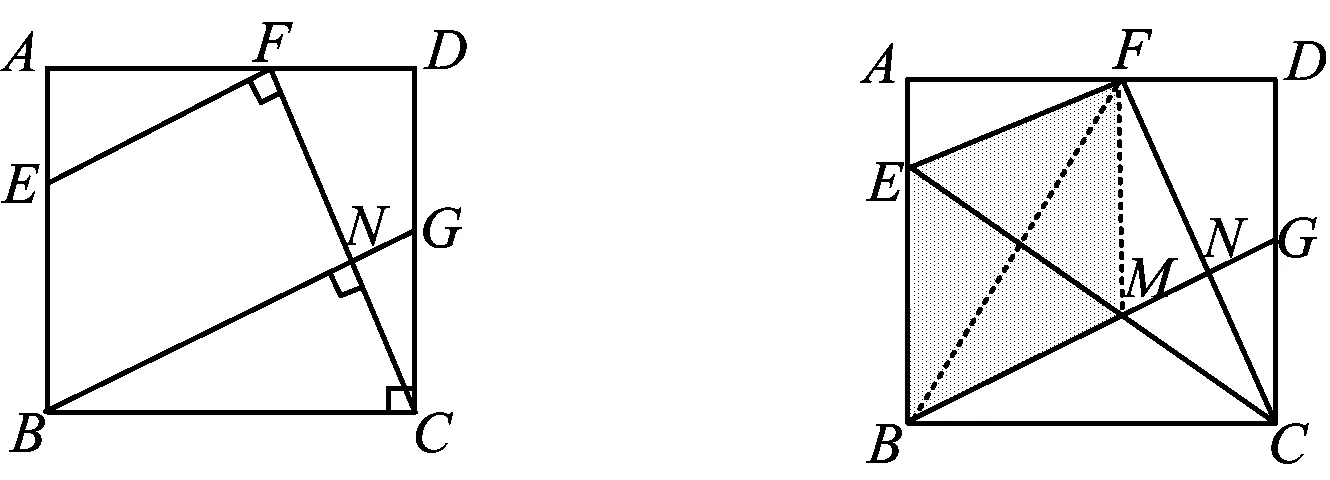
图5 图6

BN=CD=2.

在Rt△BGC中，

CN⊥BG，

得

△BGC∽△CGN，

从而

12=NG(NG+2)，

解得

因此

因为∠D=∠EFC=90°，所以

∠AFE=∠GCN，

故

视角2关联轴对称和等腰得菱形.

解法4(利用菱形构造全等和相似)如图6，联结FM,BF，由△BEC≌△FEC和BM=BE，得EF∥BM.因为BE=EF，所以四边形BEFM为菱形且∠BNF=∠EFC=90°.又BF平分∠ABN，从而

Rt△ABF≌Rt△NBF(AAS)，

得

BN=AB=2.

设BE=BM=EF=x，则

AE=2-x，MN=2-x，FM=x,NG=1+x-2=x-1.

因为FM∥GC，所以

△FMN∽△CGN，

得

即

解得

故

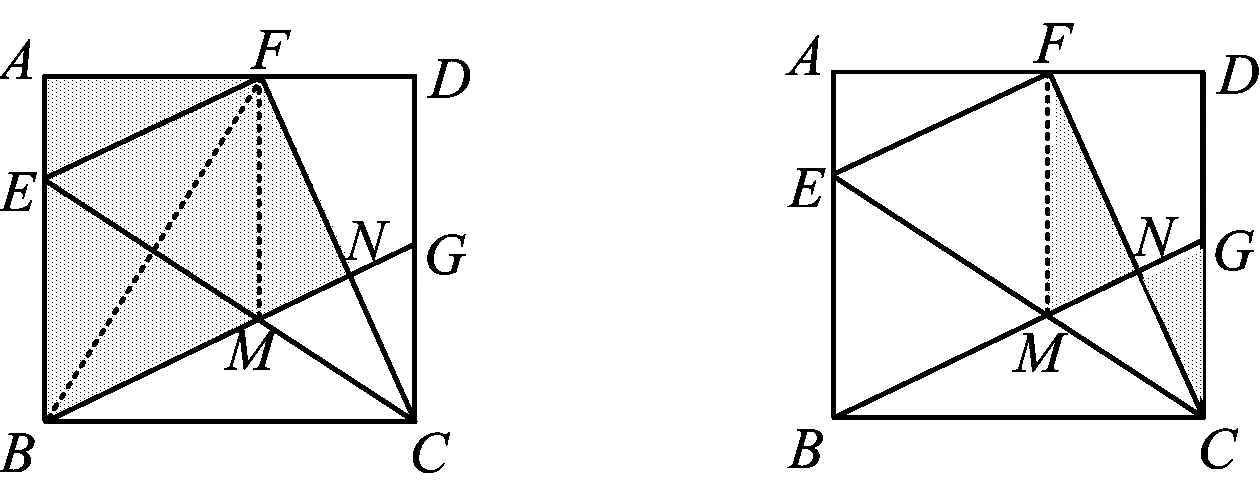
图7 图8

如图6～8，从关联基本图形分析，折叠得筝形，关联等腰进一步得菱形，利用菱形的角平分线性质得三角形全等，从而BN=AB=2，利用八字型相似可求得x的值.此方法可能是命题者想要的，可是对学生的识图能力、知识综合运用能力、逻辑推理能力要求较高.

视角3关联轴对称和垂直得相似.

解法5(矩形中的十字架)如图9，联结BF，由轴对称得EC垂直平分BF.因为∠A=∠ABC=90°，所以

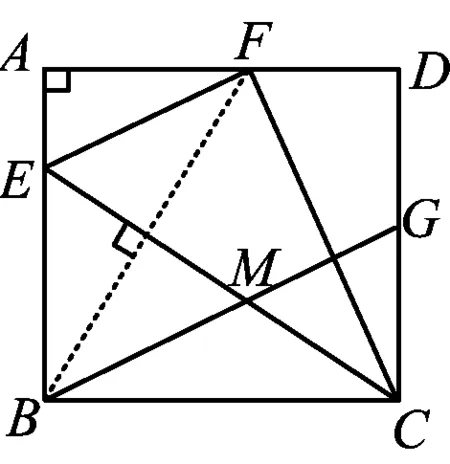
图9

Rt△AFB∽Rt△BEC，

得

设BE=BM=EF=x，则

AE=2-x.

由勾股定理，得

从而

解得

故

解法6(一线三垂直)如图1，由轴对称得△BEC≌△FEC，从而∠EFC=90°.因为∠A=∠D=90°，所以△AFE∽△DCF，得

设BE=BM=EF=x，则

AE=2-x.

由勾股定理，得

从而

解得

于是

3 问题思考

对本题的条件、结论进行分析，我们发现有许多地方值得进一步思考与探究.

思考1针对第二空，第一空BN的长是否为必要的提示？

不是.从解法1,2,5,6可以看到，无需知道BN的长就可求sin∠AFE的值；而从解法3,4可以看到，要求BN的长需要证全等，此推理过程不简单.也许命题者的用意是为了减少压轴的分值.

思考2条件“MG=1”是否为必要的条件？

不是.只是为了降低难度.更一般的情形，可设MG=a，则CD=AB=2a，参照解法1可得Rt△AFE∽Rt△CBG.设BE=BM=EF=x，则

AE=2a-x，BG=a+x，

得

解得

故

思考3条件“点G为CD的中点”是否可由特殊变为一般？

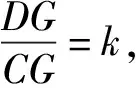
CD=AB=ak+a，

参照解法1,得

Rt△AFE∽Rt△CBG.

设BE=BM=EF=x，则

AE=ak+a-x，BG=a+x，

得

化简得

x2+(a-ak)x-a2-a2k=0，

从而Δ=(k2+2k+5)a2>0恒成立.又因为x>0,所以

故sin∠AFE自然可求.

思考4条件“BE=BM”能否扩大为“△BEM为等腰三角形”？

可以.其他两种情形：1)当BE=EM时，由AB∥CD，得CM=CG，设CD=AB=2m，BE=EM=EF=x，则

参照解法6，由一线三垂直得Rt△AFE∽Rt△DCF，从而

又

即

化简得

x2-mx-m2=0，

解得

故

2)当MB=ME时，M为Rt△BEC斜边的中点，则E为AB的中点，故满足条件的点F不存在.

思考5改变条件“点F的位置在边AD上”，可以吗？

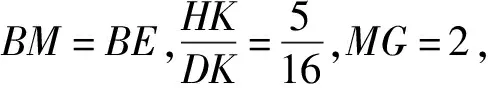
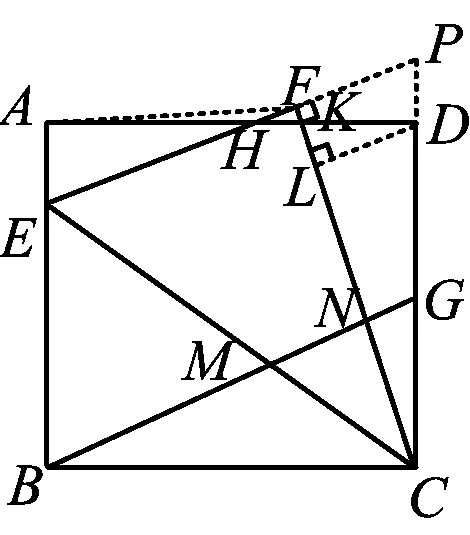
图10

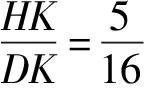
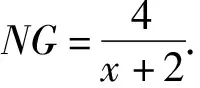
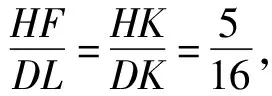
又BC=FC，易证Rt△BCG≌Rt△CFP，得

PF=CG=2，BG=PC=x+2,

从而

由△BGC∽△HPD，得

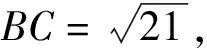
因为∠EAK=∠EFK=90°，所以点A,E,K,F共圆，得

∠AFE=∠AKE，

故

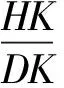
图11 图12

思考6改变背景，把矩形改为菱形可以吗？

可以.如图12，把矩形改成菱形，其他条件不变时，上述关联的图形中很多结论依然成立，如EF∥BM,四边形BEFM为菱形,△AFE∽△CBG,△ABF≌△NBF,△BNC≌△CDF等.参照解法1,得

设BE=EF=x，得

4 解后反思

4.1 提高识图能力，培养几何直观

识图能力是解决几何问题的基础，也是培养几何直观的重要基石.在平时的教学中，教师不仅要让学生观察、分析图形各元素之间的关系，更要鼓励学生多画图，特别是根据题目的文字语言画图，在画图中学生会对图形的性质有更深刻的理解[1].如本文中，在较复杂的图形中分离出轴对称、等腰、矩形等基本图形，然后把某些元素重新关联产生如菱形、平行、相似等新的图形或关系，运用新图形或关系蕴涵的性质进行推理、计算，从而找到解题的突破口.教师要教会学生在复杂图形中辨识基本图形、分解图形、关联图形、挖掘隐含信息、综合处理各知识交汇点，引导学生从整体、联系的角度分析图形，做到局部与局部、局部与整体之间的自由切换，进而提高学生的识图能力、构图能力和分析推理能力.

4.2 全面回顾与反思，发展核心素养

解题教学如果仅限于解题，不能举一反三，那么学生必将陷入题海.我们应当通过“方法论的重建”使得相应的解题活动对学生而言真正成为“可以理解的，可以学到手和可以推广应用的”[2].教师要引导学生深入探究问题的条件、结论，分析内在联系，多问“我正在做什么”“为什么要这样做”“还有其他方法吗”“可以改变题目的条件或结论吗”，即让学生沉下心来对解题活动进行全面回顾、总结和反思，把握好每一类数学问题的本质，从更高层次思考问题，这样才能真正提高学生的思维能力，提升核心素养.