例谈概念在问题解决中的作用

徐道奎

(1.金寨第一中学,安徽 金寨 237300；2.徐道奎名师工作室,安徽 金寨 237300)

概念教学是数学教学的重头戏，概念的重要性不仅体现在知识的形成过程，在解题中也非常重要，数学问题的解决很多都是通过概念切入，依靠概念寻求问题解决的逻辑线索和逻辑关系的.解题过程往往是分析概念、应用概念的过程，概念是问题解决的基础和逻辑起点.没有真正地理解和领悟概念，就会感到问题解决“无从下手”，缺少核心，没有灵魂[1].

1 依据概念切入

从概念切入，就是对问题中涉及的关键概念进行解读，搞清楚这个关键概念是什么？什么含义？需要解决的问题如何通过概念得到转化，通过概念得出问题解决的方法.

例1已知正方体的棱长为1，每条棱所在的直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为

( )

(2018年全国数学高考理科试题Ⅰ第12题)

分析这是一个线面角概念的应用问题，我们从线面角的概念切入.

1)由线面角概念可知线面角实为线线角(平面外直线与其在平面内的射影的夹角).线面角(除线面垂直和平行)可以通过斜线上的点到平面的“垂直距离”和“斜距离”(斜线上的点到该直线与平面斜足之间线段长)的比求出正弦值.

2)求线与线夹角时，要注意把“线”“平移”，因为“平移”不改变夹角，因此，“所有棱”(12条)实际上可以转化为“3条棱”.

3)“3条棱”再转化为从同一个顶点出发的3条棱，从而得到一个截面.这样，先把满足条件的截面之一找到.考虑从点A1出发的3条棱A1B1,A1D1,A1A(如图1)，则平面AB1D1即是一个截面，记为α.

图1

4)面积的最大截面应该与截面α平行，那么，哪一个符合要求呢？平行移动平面α，由对称性可知，当截面α经过正方体相应的6条棱的中点时截面面积最大.

分析从函数极大值概念入手.第一，函数极值点是导数的变号零点；第二，极大值点是原函数单调区间的“界点”，在极大值点处，单调区间为“前增后减”，对应的导数符号是“前正后负”.因此，先求出导数的“变号零点”，再分析零点处函数单调性的变化.

2 围绕概念分析

求解一个问题，有时涉及多个概念，要分析每个概念在问题解决中的作用，通过概念的分析去寻找解题的逻辑线索和逻辑关系.

例3设f(x)是定义在R上的偶函数，且当x≤0时，f(x)=log4(3-x).若对于任意的x∈[0,b+1]，均有f(x+b)≥f(2x)，则实数b的最大值是

( )

(2021年皖豫名校联盟第3次联考数学试题第12题)

分析这是一个关于函数性质和不等式恒成立综合运用的问题，题目涉及多个概念.

偶函数的有关概念：

1)由f(x)是偶函数，联想到偶函数的性质(对称性、单调性)，同时注意到：如果需要，我们可以求出f(x)在x≥0(注意：本题等号也可以放在这里)时的解析式.

2)在不等式f(x+b)≥f(2x)进行转化时，一般有两种思路：一是将“整体变量”x+b和2x代入函数解析式，把不等式两边变成具体的代数式；二是利用函数单调性，把函数值大小变成整体变量x+b和2x的不等关系.两种方法相比，利用函数单调性较为简单.由条件可知2x≥0，但不知道x+b是大于等于0还是小于等于0，因此，根据偶函数的性质和当x≥0时函数的单调性，不等式可转化为

|x+b|≥2x,

(1)

则问题转化为式(1)在[0,b+1]上的恒成立问题.

问题涉及不等式恒成立概念，而不等式恒成立与函数、解不等式均有联系，不等式恒成立有多种解法，这里直接求出式(1)的解集D(需要对b进行讨论)，只要满足D⊆[0,b+1]即可，答案为B.

3 进入概念情境

解题时，我们经常会遇到“即时定义”的“新”概念，这时必须进入问题所设置的概念情境(实践情境、学术情境)，揣摩、领悟概念的“意义”“含义”，顺应概念，依据“概念”的意义和“指引”，分析线索，寻找关系.

1)求四棱锥的总曲率；

2)若多面体满足：顶点数-棱数+面数=2，证明：这类多面体的总曲率是常数.

(2021年“八省市”联考数学试题第20题)

分析进入“多面体顶点曲率”的概念情境，即：什么是多面体每个顶点的曲率？什么是多面体的总曲率？

1)由多面体曲率概念，四棱锥的总曲率为5个顶点的曲率之和，注意到多面体各顶点面角不需要单独计算，可以整体考虑(一个四边形，4个三角形)，因此，四棱锥的总曲率为5×2π-2π-4×π=4π.

2)多面体是不确定的，但顶点数、棱数、面数有一个固定关系，由多面体曲率概念，必须知道多面体的顶点个数、面的个数以及每一个面对应的多边形内角和，由题意和多面体顶点曲率的概念，可以梳理出以下关系：

①根据顶点数、棱数、面数的关系，设出其中两个，表示出第3个，不妨设顶点个数为n，面的个数为k，则棱数为n+k-2；

②每个面是几边形，由这个面的棱的个数确定；

③每一条棱同时在两个面上(一条棱用2次)；

例5阿波罗尼斯是古希腊数学家，他与阿基米德、欧几里得齐名，以他的名字命名的阿波罗尼斯圆是指平面内到两定点的距离的比值为定值λ(其中λ>0,λ≠1)的动点的轨迹.已知在△ABC中，角A，B，C所对的边分别为a，b，c，且sinA=2sinB，acosB+bcosA=2,则△ABC面积的最大值为

( )

(2020年江淮十校数学第二次联考理科试题第9题)

图2

4 进行概念辨析

问题的顺利解决需要理解概念含义，综合运用概念，尤其要对相关相近的概念进行辨析，分析概念的异同点.

分析这是两个解决方法相近的问题，把它们选在一起有利于学生辨析、理解.问题涉及导数正负与函数单调性关系的概念以及全称性命题与存在性命题的概念.为什么第1)小题中f′(x)≤0，(注意：必须带等号，且这里的等于0非恒等于0)，而第2)小题中f′(x)>0(注意：不能带等号)？要通过单调区间的概念和命题的有关概念引导学生分析.

例7已知函数f(x)=xlnx-ax+1，其中a∈R，若函数f(x)的值域为[0,+∞)，求a.

分析函数f(x)的值域为[0,+∞)与函数f(x)≥0是意义不同的两个概念，解法不同.虽然都需要求导、分析函数图像，得出函数最小值,但前者是最小值等于0，而后者是最小值大于等于0.

5 把握概念意义

知识形成过程中，会产生许多概念，而产生的每一个概念都有一定的意义背景、一定的适用条件、一定的形式结构，只有真正掌握概念的意义，才能通过概念便捷地解决问题.

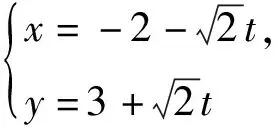
1)求直线l的普通方程与曲线C的直角坐标方程；

2)设直线l交曲线C于点A,B，点P的直角坐标为(-2,3)，求|PA|·|PB|的值.

第2)小题中，(-2,3)在直线上，但题目给出的直线参数方程非“标准形式”，|t|就没有相应的“几何意义”，如果想用直线参数方程中参数的几何意义解题，那么必须把参数方程“标准形式化”，如我们可以将参数方程写成

(2)

6 领悟概念本质

数学知识是一个联系的整体，理解和应用概念，要整体把握概念的本质.《普通高中数学课程标准(2017年版2020年修订)》中指出，函数是高中数学必修内容的一个重要的“主题”，函数是整个数学大厦的基础，数列、不等式、解析几何、概率等很多问题归根到底都是函数问题，解决上述问题应该回归到函数概念上来.

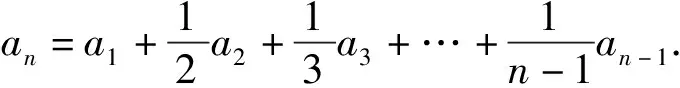
1)求{an}的通项公式；

分析数列的本质是函数，数列问题要有函数的视角，函数问题应注意定义域，而数列问题要注意n(自变量)的取值范围.

第1)小题需要把式子

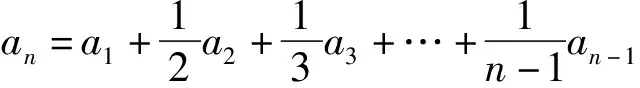
(3)

进行迭代，迭代后，n的范围发生了改变，即

(4)

两式相减，得

即

进一步迭代可以得到

7 理解概念原理

概念的应用不能止于表面，不能流于形式上的“对号入座”，而要把握本质，尤其要理解概念所反映的数学原理.

用不等式性质求解最值问题实际上是函数最值概念的运用，以函数最小值定义为例(最大值定义类似)：一般地，设函数y=f(x)的定义域为I，如果存在实数m满足：1)对于任意的x∈I，都有f(x)≥m；2)存在x0∈I,使得f(x0)=m，那么我们称m是函数y=f(x)的最小值.函数最小值的概念强调了两点:一是所有函数值都比实数m大;二是“有”函数值等于m的情况存在.不理解概念，就不能真正理解用不等式性质求解函数最值问题的实质，从而出现错误.“均值不等式”“柯西不等式”“绝对值性质不等式”等这些含有等号的不等式均可以用来求解最值，其原理就是函数最值的概念.用性质不等式求解最值，结果必须是“定值”，等号必须“取得到”，实际上就是函数“最值”的概念的体现.

例10设函数f(x)=|x+1|+|2x+a|的最小值为3，则实数a的值为

( )

A.5或8 B.-1或5

C.-1或-4 D.-4或8

(2014年安徽省数学高考理科试题第9题)

分析此题解法很多.我们用最值的概念和性质不等式求解最值的概念和原理进行分析[4].

由于

f(x)=|x+1|+|2x+a|

8 结束语

解题要依据概念进行分析，反过来，通过解题又可以强化对概念的理解.因此，概念是数学解题教学的抓手.概念是问题解决的基础，解题时要抓住概念，依据概念，分析概念，围绕概念找关系.不仅要理解概念的意义，而且关键概念、核心概念的生成过程、概念体系的形成过程也要清晰.要充分认识概念在问题解决过程中的重要性，不能本末倒置，要杜绝抛弃概念机械刷题的做法.