重视概念生成 深化概念认知——以人教版“反比例函数”第一课时教学为例

顾 勇

(正余初级中学，江苏 南通 226153)

数学概念是反映现实世界空间形式和数量关系本质属性的思维形式.数学概念是非常抽象的，初中生受年龄、经验和认知等方面的限制，对教材中概念的接受和掌握是不易的.概念教学是数学教学的一种课型，本文以义务教育人教版《数学》第26.1节“反比例函数”概念课教学为例，以抛砖引玉.

1 课堂实录

1.1 情境引入，感知概念

问题1(视频展示中国高铁)我国的高铁在世界上的名气很大，可以说高铁是中国展示给世界的一张亮丽名片，很多国家都希望在高铁项目上能与中国有合作.那么问题来了，在同一条铁路线上，不同车次的列车运行时间有的长有的短，因此它们的平均速度有快有慢，这有什么规律呢？

设计意图数学学科如何渗透德育？情境选择是关键.中国高铁无疑可以成为本课最佳的现实情境，以此来增强学生的民族自豪感，是一次难得的爱国主义教育机会.爱国主义是中华民族精神的核心，是中华文明源远流长的内在精神动力，也是千百年来中国人民团结统一、自强不息的精神支撑.同时行程类问题的模型又是本课的切入口.在路程s一定的前提下，平均速度v与运行时间t具有反比例变化的规律，让学生初步感知概念.

问题2在下列实际问题中，分别写出两个变量之间的关系.

1)一辆以60 km/h匀速行驶的汽车，它行驶的距离s(单位：km)随时间t(单位：h)的变化而变化，则s=______.

2)体育课上，教师测试了百米赛跑，那么，平均速度v(单位：m/s)随着时间t(单位：s)的变化而变化，则v=______.

3)小明家有一面积为1 000 m2的矩形草坪，草坪的长为y(单位：m)随宽为x(单位：m)的变化而变化，则y=______.

4)已知海门区的总面积为1 148 km2，人均占地面积s(单位：km2/人)随全市总人口n(单位：人)的变化而变化，则s=______.

5)△ABC的面积为10 cm2，它的一条边长为xcm，这条边上的高为ycm，则y=______.

设计意图问题2的设计，让学生借助已有的数学模型(路程=速度×时间，矩形面积=长×宽，人均占地面积=总面积÷总人口，三角形的面积=底×高÷2)，很快可以列出数量关系式，但其中又有未学过的函数关系式，这样就能激起学生探究新函数的热情.同时不同模型下的函数关系又有相同的特征，这样便于学生归纳出两个变量之间的反比例函数关系，为下一步形成概念做铺垫.

1.2 师生互动，初识概念

教师让5位学生上黑板展示上述5个问题的关系式：

师：在上面的关系式中，有我们学过的函数关系式吗？

生1：1)s=60t是正比例函数.

师：剩下的4个关系式具有怎样的共同特征？

生2：它们都有两个变量，其中一个变量在分母上.

生3(补充)：分母中的变量不能为0，分子中的常量都不为0.

生4(补充)：两个变量中一个变大，另一个就变小，成反比例关系.

师：3位同学回答得很好！我们前面学习过正比例函数，它们之间有怎样的联系和区别呢？

设计意图概念的生成往往是一个逐步抽象的过程，但是要求学生一次抽象成功是不现实的，因为每个学生的认知水平不一样，看待关系式的角度和深度有很大差别.因此，通过师生互动问答，教师可以起到引导方向的作用，但主旋律还是以学生为主体，让学生通过类比正比例函数的概念，在学生的不断补充中完善了对概念内涵的理解.

1.3 整理分析，形成概念

师：生5的想法很好！现在哪位同学来给反比例函数下一个定义？

师：生6类比思想用得非常好！其他同学对他的定义有没有要补充的呢？

生7：x不能取0.

设计意图生6的回答超出了教师的预设，教师直接把正比例函数的定义和反比例函数的定义都写在黑板上，这样能较好地帮助学生渗透类比思想.同时在对比两个定义时，学生就能很容易理解反比例函数中k≠0的含义了，另外对比之后又能深刻理解反比例函数中x≠0，而正比例函数中的x可以取0，从而深化了学生对整式函数与分式函数的概念认知.

1.4 深入研究，吃透概念

问题3下列函数中y是x的反比例函数的有哪些？并说出它们的比例系数k的取值？

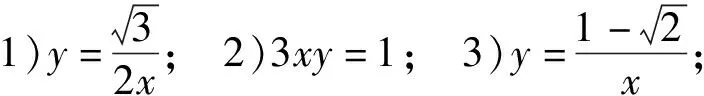
问题4已知y是x的反比例函数，当x=2时，y=6，求这个反比例函数的表达式.

问题5y是x的反比例函数，表1给出了x与y的一些值.请补全表1并求出这个反比例函数的解析式.

表1 反比例函数中x与y的值

设计意图问题3中学生能很容易找到函数1)和函数3)是反比例函数，但不能马上看出函数2)是反比例函数，这时教师要在黑板上进行变形讲解.还有一个难点与学单项式时类似，函数1)中的系数k有部分学生确定不了，这时教师需要耐心讲解，确保学生能吃透定义.问题4的设计是让学生内化一种数学方法叫做待定系数法，问题5的设计是让学生直观理解函数的表达形式除了有解析式之外还有表格式，后面还有图像式.

1.5 变式练习，内化概念

问题6已知y与x2成反比例，当x=2时，y=6.

1)写出y和x的函数解析式;

2)求当x=3时，y的值;

3)求当y=12时，x的值.

1.6 回顾前路，回品概念

1)我们是怎样得到反比例函数概念的？

2)你是如何理解反比例函数定义的？

3)在反比例函数的学习过程中，我们用到了哪些数学思想(可以结合具体问题说明)？

设计意图学习是一个自我认知的过程，一节课的探究，首先是零散式地解决了一个个问题，形成了数学概念初步，认知仍处于表层，视域还不宽，深度还不够，因此小结反思是必不可少的课堂环节.教师引导学生从数学思想这一主干入手，整体把握知识的生成，如此学生就不用“盲人摸象”.同时反思小结是学生学习数学所不可缺少的环节，能更好地帮助学生从整体上掌握所学的知识和方法，便于学生触类旁通，有助于学生从题海中解放出来，逐步体会到一些重要的数学思想，优化思维品质，从而懂得如何学习，同时也培养了学生爱思考、爱质疑的良好习惯.

2 教学价值分析

2.1 规范认知顺序，助力四能提升

《义务教育数学课程标准(2011年版)》(以下简称《课标》)提出“让学生能体会数学知识之间、数学与其他学科之间、数学与生活实际之间的联系”.同时《课标》还提出“学生要能运用数学的思维方式进行思考”.要完成《课标》的目标要求，概念教学就不能就知识讲知识，应重视数学知识之间的联系，要有对旧知的回顾，更少不了对新知的探究.仅仅这样只完成了“四能”中前面的“两能”，还需要“师生互动”“变式训练”和“回品概念”来关联学科知识，增强发现和提出问题、分析与解决问题的能力.在整个学习过程中学生对数学知识的获得是通过规范的认知体系来实现的，遵循了知识的发生、发展规律，学生能以数学的眼光来发现并提出问题，还能用所学知识解决问题[1].

2.2 重视学习方法，培养认知能力

一般说来，丰富知识的习得必定离不开高效优质的学习方法.凡是优质的学习方法，教师在教学时就应该反复刺激呈现，以规范的授课流程、科学的实践方式来培养和提升学生的认知能力.本课所用的类比学习法是帮助学生成功突破反比例函数概念教学重难点的利器，设置的问题基本都能发掘类比学习的价值.本课没有完全沿用教材的流程，而是以“神州高铁”的爱国主义教育起头，以实例探究为知识发现和归纳的矿藏，引导学生以类比为催化剂，让学生对问题的每一次探究都能加深对类比认知的理解，从而让其成为终身受用的重要方法之一.

3 教后反思

3.1 重视概念形成

反比例函数在人教版《数学》九年级下册第26章，是教材安排的最后一类函数，也是中考重点考查的内容之一.函数是初中数学中重要的概念之一，它的研究方法是一脉相承的，因此给了我们规范的授课流程和实践研究的套路.本课是反比例函数的起始课，人教版教师用书九年级下册第1页指出：反比例函数是《课标》“数与式”领域的内容.其学习基础是函数的概念、函数的表示方法以及反比例关系；通过类比正比例函数、一次函数和二次函数的研究方法，研究反比例函数的概念、图像、性质及其应用[2].因此在上课前要安排复习回顾正比例函数、一次函数和二次函数的整体知识框架，理顺认知结构中的相关知识链接，找回研究套路.

因为本课的重难点均为反比例函数的概念，所以重视概念的生成过程很关键.首先，给予学生一定量的生活实例情境，让其在熟悉的数学模型之下抽象数量关系，这个过程教师不能着急，要给学生充足的时间，让其自主发现这些模型中的反比例的变化规律.其次，抽象概念时教师不能替代学生，要真正突显学生的主体地位.期间若有磕磕绊绊的现象，教师要积极引导，应“看透而不说透”，让课堂处于一种“愤悱”的认知状态，就像生6那样，最后找到类比学习法，并归纳反比例函数的概念.教师要鼓励学生去类比正比例函数的概念，如学生补充了x≠0，这也是对概念的一种内化和理解.

3.2 深化概念认知

数学概念是数学知识的基础，是数学知识结构中最基本的因素，也是数学思想方法的载体.从概念的重要性方面考虑，要求在形成概念的过程中，必须遵循科学规范的教学策略，给予学生内化的时间和空间深化对概念的认知.利用情境实例引入概念虽属理性认识，但其形成依赖于感性认识，学生的心理特征倾向于理解和接受，这时的概念认知属于知道概念，学生对概念的识别尚属浅层次.因此，注重概念形成的过程，是符合学生的概念认识规律的.概念的形成过程可以完整地、本质地揭示概念的本质属性，使学生对理解概念具备思想基础，同时也能培养学生从具体到抽象的思维方法.理解概念是概念教学的核心，典型例题、变式训练以及师生、生生互动合作，可以让学生进一步完善概念认知，获得解题技能、解题策略，同时还能反哺认识，把反比例函数和谐地纳入函数家族，形成变量数学意识.从量变到质变，要深入内化概念，更深刻地理解和掌握概念的内涵和外延，与此同时还得把概念认知再放到实际问题中去，从问题中来再回到问题中去，在落实问题解决能力的同时还规范了概念研究的套路.

李邦河院士曾说：“根据我上大学以后搞数学研究的经验，数学根本上是玩概念，不是玩技巧.技巧不足道也！”可见概念学习对学生的数学学习有着至关重要的作用，教师在概念教学时要放慢概念认识过程的步伐，让学生更充分地知道概念；要细化概念归纳的过程，让学生更全面地理解概念；要善于应用和回品概念，让学生更完整地认识概念.