螺栓连接大变形梁非线性振动特性的实验研究

张 珂，张毅雄，冯志鹏，黄 旋，陈 果

中国核动力研究设计院核反应堆设计技术重点实验室，四川 成都 610213

引言

在核工程、航天航空等领域存在着大量的螺栓连接，对系统的安全运行影响十分显著，连接处的非线性特性会影响结构响应，当连接失效时甚至会引起结构破坏等严重后果，而当核动力装置中的管道等柔性构件发生大幅运动时，几何非线性因素对结构振动响应的影响也不容小觑。目前，对于几何非线性和螺栓连接的分析方法比较保守，且以理论分析居多。为提高分析精度，提取非线性模态特征，验证理论结果，通过实验研究多种非线性因素共同作用下的振动响应是有必要的。

非线性系统包含了许多极度复杂的行为，如：突跳、分叉、饱和、次谐波和超谐波、内共振、极限环、模态混叠以及混沌[1-5]。线性模态无法解释这类复杂的动力学行为，因此，学者提出了非线性模态的概念进行研究，随着研究的深入和计算能力的增强，非线性模态逐渐开始在工程领域中应用。2017 年，Liang等[6]以输送流体的管道为例，对陀螺连续体的强迫振动进行分析，利用谐波平衡法和不变流形思想求解了它的非线性模态。2018 年，Gao 等[7]在通过实验和数值的方法分析了内共振条件下的在轨可展开天线的非线性动力学特性，结果表明在大范围的失谐参数上存在不止一种非线性模态。

针对连接处间隙碰撞、滑移等因素引起的非线性特性，中外学者以连接处的非线性刚度和非线性阻尼为切入点，提出了多种动力学建模方法[8-13]。针对柔性梁的动力学响应分析，目前常见的方法包括：KED 法[14]、混合坐标法[15]、绝对节点坐标法[16]和几何精确梁模型[17-18]，近年来的研究主要针对提升算法的效率和应用[19-21]。目前，对于同时含有螺栓连接和几何大变形的结构动力学响应研究较少，因此，本文搭建了螺栓连接大变形梁的实验台架，通过实验测试分析其模态、阻尼、响应特性，研究两种非线性因素耦合作用的模态特征。

1 理论模型

Peeters 等[22]指出，激励能量的变化会引起非线性模态频率的变化，并通过实验与数值结果的对比，说明当响应与激励信号是正交的同周期运动时，可以激励得到结构的非线性模态，基于相位滞后准则建立了结构非线性模态的实验测试方法。

本文针对工程中常见的螺栓连接柔性结构，利用Song 等[23]对于连接部件提出的改进Iwan 模型和Bathe[24]对于大变形结构提出的updated-lagrange混合坐标法，建立了含连接结构大变形梁的动力学模型

本文利用Kerschen 提出的基于相位滞后准则的非线性模态实验测试方法，通过实验测试研究同时含有连接处非线性因素和大变形非线性因素的结构非线性模态特性，对两种非线性因素耦合作用下激励能量对模态频率影响的规律进行研究。

2 实验系统及试件

实验系统由试件、夹具、激励系统、数据采集与处理系统组成，实验台见图1，实验流程见图2，计算机产生激励信号，通过功率放大器使激振器激励试件振动，传感器采集振动的位移和激励力信号，通过数据采集卡将响应信号返回计算机并进行后处理。

图1 实验台实物图Fig.1 Experiment device

图2 实验流程图Fig.2 Sketch of experimental system

本次实验的主要设备是使用螺栓连接的柔性梁，试件是两根长度l=0.300 m，宽度d=0.025 m，厚度w=0.001 m 的钢质梁，通过两个M5 的螺栓连接，螺栓的预紧扭矩为0.12 N·m，连接处重叠部分长度为0.020 m。通过定制的夹具构成一端固定一端自由的悬臂梁，激振器作用位置距根部距离L0=0.002 m，激光位移传感器的两个测点P1、P2距根部距离分别为L1=0.220 m，L2=0.360 m。模型示意图见图3。

图3 模型示意图Fig.3 Sketch of test model

在实验过程中，发现激振器的激振力不总是恒定的，尤其是当扫频激励中频率接近共振频率时，力传感器测得的激振力会出现明显上升的情况。图4是0～100 s，0～50 Hz 扫频测得的激振力图像，可以看出，在非共振时间的力幅值为3 N，但是在29 s和86 s 附近，力幅值出现了短暂而明显的上升。为了排除力幅值的变化对于测试结果的影响，加入反馈控制，可保证激振力输出稳定，如图5 所示。

图4 无控制扫频激振力Fig.4 Uncontrolled sweep exciting force

图5 反馈控制扫频激振力Fig.5 Sweep exciting force under feedback control

3 正弦定频激励

为研究连接构件对结构共振频率和共振时位移响应的影响，设置对照实验，连续梁试件宽度和厚度与图3 中连接梁试件相同，长度为0.6 m，其他条件控制完全相同，进行如下实验测试。

施加定频激励信号，采用步进正弦激励的方式，在各阶共振频率附近以较小的步长逐步改变激励频率，并在达到稳态后测量激振力和位移的相位差，利用相位差滞后准则：激振力和响应位移的相位差达到90°时认为激励起了非线性模态，得到了结构在前三阶共振情况下的频率和位移响应幅值如表1所示。分析实验结果可知，连续梁和连接梁在共振时的位移幅值远远超过梁在振动方向的厚度，发生了大变形；螺栓连接的存在使结构的二三阶共振频率下降；连接梁和连续梁都在各自的共振频率，在激振力相近的情况下，连接梁的位移幅值更小，说明螺栓连接表现出更强的阻尼特性。

表1 定频激励频率-位移响应Tab.1 Frequency-displacement response under fixed frequency excitation

4 正弦扫频激励

非线性模态一个重要的特性是模态频率会随着激励能量的改变而改变，频响函数可以直观地体现结构频率和响应的关系，从而方便研究模态特性。使用线性正弦扫频，扫频频率为0～100 Hz，设置3个大小等级的激振力：小激振力0.80 N，中激振力3.00 N，大激振力10.00 N。实验结果如图6 所示。

通过图6a、图6b 可以得出，不同激振力下，扫频的结构位移响应趋势基本相同，位移响应幅值和激振力正相关。图6c、图6d 是不同激振力下频响函数的对比，结合表2 可以看出，第二、三、四阶的频响函数都随着激振力的增大而出现了左偏的趋势，即出现了随着激励能量的增大，模态频率减小的非线性模态现象。

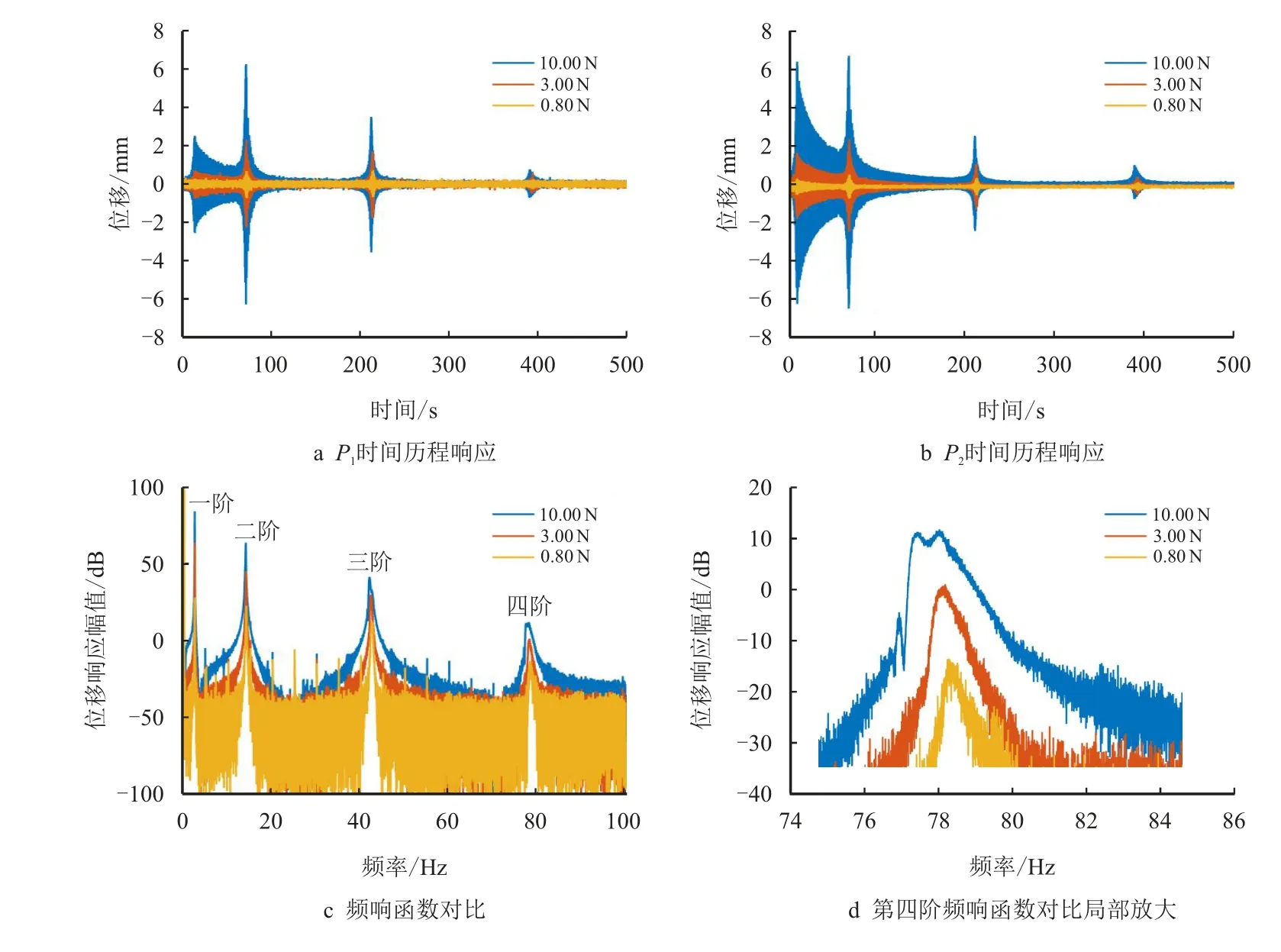
图6 改变激振力正弦扫频实验图Fig.6 Sine sweep experiment diagram with different exciting force

表2 改变激振力扫频各阶模态频率对比Tab.2 Modal frequency comparison with different exciting forces

Song 的研究指出，螺栓连接结构处存在的非线性滑移行为会导致结构的模态频率随激励能量的增大而减小；而几何大变形的公式推导则清晰地表明横向大变形引起的轴向应变不可忽略时，会为系统引入额外的非线性刚度，即结构的模态频率会随着激励能量的增大而增大。

本文的实验结论说明，当连接非线性因素与几何非线性因素耦合作用时，滑移引起的刚度减弱效果强于大变形引起的刚度附加，导致结构整体表现出模态频率随着激励能量增大而增大的非线性特性。

使用半功率点法，根据所测得的位移响应的频响函数值，计算不同激振力下的各阶模态阻尼比，结果如表3 所示，可以得到，随着激振力增大，振幅增加，结构阻尼也随之明显增加的非线性现象。

表3 改变激振力扫频各阶模态阻尼比对比Tab.3 Modal damping comparison with different exciting forces

5 改变预紧力扫频激励

含连接构件大变形梁的非线性因素由连接界面的滑移引起，通过改变连接处螺栓的预紧力，可以改变连接界面接触刚度和滑移发生的困难程度，从而改变能量耗散的程度。实验通过数显扭力扳手定量地控制螺栓连接的扭矩，设置3 组不同的预紧力实验组，其预紧力分别为0.15，0.25 和0.95 N·m，研究不同预紧力下扫频激励得到的结构模态的区别。

结合图7 和表4 可以得出，第二三阶的频响函数都随着激振力的增大而出现了向右平移的趋势，即出现了随着预紧力增大，模态频率略微增大的现象。

图7 改变预紧力正弦扫频实验图Fig.7 Sine sweep experiment diagram with different preloads

表4 改变预紧力扫频各阶模态频率对比Tab.4 Modal frequency comparison with different preloads

6 改变连接位置扫频激励

螺栓连接处可能造成刚度硬化、间隙、滑移等非线性现象，引起结构的模态频率或振型的改变，因此，为了研究螺栓连接位置对结构模态频率的影响，制作3 组试件，进行扫频实验对比其模态频率。

图8 从上至下依次是螺栓连接位置距固定端180～200 mm（靠前连接），距固定端280～300 mm（居中连接），距固定端460～480 mm（靠后连接）3 个实验试件。控制预紧力为0.30 N·m，其他条件完全相同，对不同螺栓连接位置的3 根试件进行扫频实验，结果如表5 所示和图9 所示。

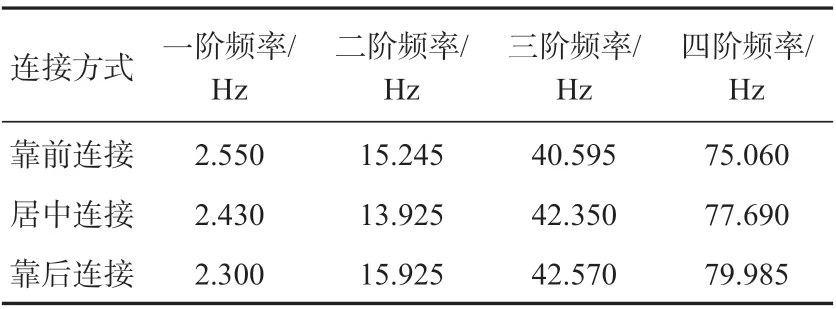
表5 改变连接位置扫频实验结果Tab.5 Sine sweep experiment result with different bolt connection positions

图8 不同螺栓连接位置试件实物图Fig.8 Specimen with different bolt connection positions

图9 改变连接位置扫频频响函数对比Fig.9 Comparison of FRFs with different bolt connection positions

实验表明，改变螺栓连接位置对结构固有频率的影响相当明显，且其规律并不是直观的，和连接位置与固定端距离线性相关，使用线性模型，即通过建立的有限元模型整体质量矩阵M和整体刚度矩阵K，基于矩阵求特征值的方式，数值求解定性地展示连接位置对模态频率的影响。

改变连接处位置，得到系统的前四阶频率与连接处位置的关系如图10 所示。

图10 连接处位置与模态频率的关系Fig.10 The relationship between the position of the connection and the modal frequency

螺栓连接处附加了螺栓的质量，会导致连接处单元质量增加，因此，在线性定性计算中，通过测量螺栓的质量和计算连接处重叠部分梁的质量，近似假设连接处的单元质量满足m′=2m（m′连接处梁单元的质量，kg；m普通梁单元的质量，kg）。且连接处由于滑移等因素会造成刚度下降，刚度的削减与运动的幅值和速度有关，是一个非线性量，为定性分析简化计算，在线性计算中近似选取单元刚度为k′=0.7k（k′连接处梁单元的刚度，N/m；k普通梁单元的刚度，N/m）。

可以看出，结构的模态频率与连接处位置呈波动变化，而不是简单的与固定端距离呈线性关系。具体改变连接处位置数值计算的频率见表6。

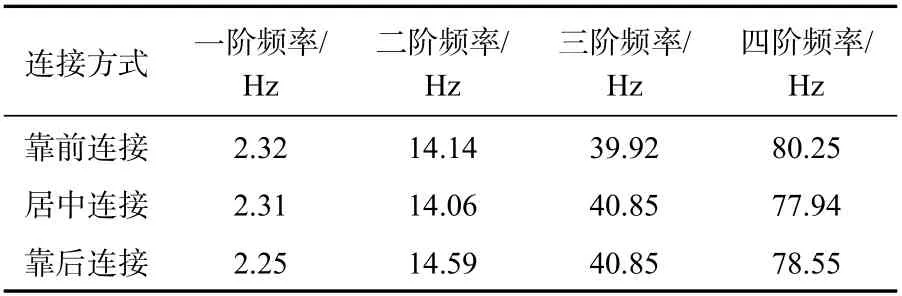
表6 改变连接处位置结构模态频率Tab.6 Modal frequency comparison with different bolt connection positions

对比数值计算和实验测试的结果可知，虽然由于线性计算的误差问题导致具体的数值有一定差异，但是前三阶频率与连接位置的关系趋势相同，说明使用此种简化方法可以在一定程度上反映连接处位置与模态频率的关系，且在工业中对需要迅速定性判断结构频率有较好的应用效果。

7 结论

（1）针对核反应堆系统中常见的螺栓连接和柔性构件，以含螺栓连接结构的大变形柔性梁为研究对象，通过实验研究分析其振动特性，获得同时包含连接非线性因素和大变形几何非线性因素的结构非线性模态特征和规律，为含连接构件组件的设计优化提供技术支撑。

（2）基于激光位移传感器搭建了非接触式的实验台架，进行了连续梁和连接梁的定频、扫频等不同激励模式的实验测试。得到的实验现象和结论有：薄长梁在共振时发生大变形；螺栓连接的存在导致结构频率降低，共振幅值减小，阻尼增大；增大激振力，连接梁出现频率软化的非线性模态现象；改变连接处位置，结构模态频率出现明显改变，其规律可以通过求解特征矩阵的方式定性预测。

（3）当连接非线性因素与几何非线性因素耦合作用时，滑移引起的刚度减弱效果强于大变形引起的刚度附加，导致结构整体表现出模态频率随着激励能量增大而增大的非线性特性。