正弦扫频速率对结构响应的影响分析

高 强，吴艳红，栾金择，李京霖

（航天科工空间工程发展有限公司，北京100854）

0 引言

在飞行器研制过程中，常通过正弦扫频振动试验来考核飞行器结构在低频段的性能[1]，亦可根据振动试验的结构响应数据得到结构主模态信息（共振频率、放大系数等）[2-3]并进行有限元模型修正。

在正弦扫频振动中，激励频率随时间变化，因此正弦扫频振动为非稳态振动，结构响应与稳态振动响应间存在差异，具体表现为：峰值减小，正向扫频激励下峰值频率右移（逆向扫频激励下峰值频率左移）、共振峰形状扭曲，且扫频速率越高，上述特征越明显[4-8]。因此直接使用正弦扫频振动试验数据进行有限元模型修正会引入新的误差。文献[4-8]对正弦扫频激励下的扫频响应特性进行了分析，但未得出明确的扫频响应特性与扫频速率间关系式，且未对多自由度系统的扫频特性进行研究。

本文使用数值积分方法研究单自由度系统在正弦扫频激励下的响应特性，推导了一个量纲为1的扫频参数η，得到了结构的响应特性与η的关系式；在扫频参数η相同，其他参数不同的情况下，系统响应特性一致。最后通过简易卫星模型证明，上述关系式亦可适用于多自由度系统在低阶模态处的扫频响应分析。

1 正弦扫频激励下的响应求解

1.1 单自由度系统

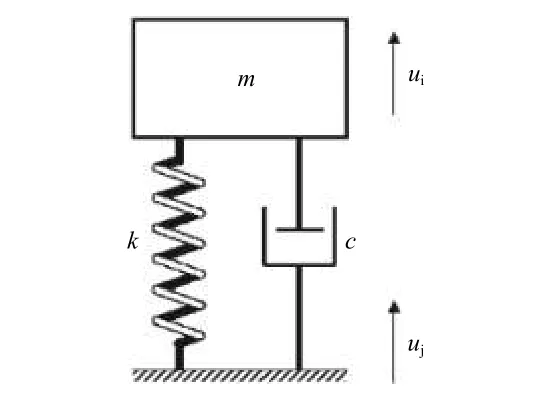
图1 单自由度系统Fig.1 Single-DOFsystem

当系统受到圆频率为ω的位移激励uj时，系统的动力学方程为

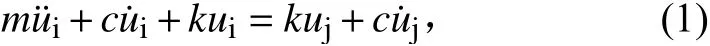
式中ui为系统的绝对位移。ui与uj的关系为

1.2 线性扫频激励和对数扫频激励

线性扫频和对数扫频是实际应用中常用的正弦扫频方式。在线性扫频中，基础激励的频率变化率为Rlinear，Hz/m in；在对数扫频中，基础激励的频率变化率为Rexp，oct/m in。正向扫频（由低到高扫频，下同）时，频率变化率为正数；逆向扫频（由高到低扫频，下同）时，频率变化率为负数。设扫频信号的初始频率为fstart，则线性扫频和对数扫频的频率分别为：

1.3 求解正弦扫频激励下系统的响应

将uj的表达式（式(7)或式(8)）代入系统的动力学方程（式(1)），即可求解得到系统响应ui。由于uj为非简谐振动，所以上述方程很难得到理论解。Cronin[9]使用泰勒级数、傅里叶展开、固定相位法和“鞍点”法等多种方法，推导了正弦扫频激励下单自由度系统响应的近似公式。但该近似公式只适用于阻尼比很小（小于0.01）、扫频速率很慢的情况，不适合进行系统振动响应特性研究。

本文使用Duhamel 数值积分方法求解单自由度系统在正弦扫频激励下的响应。为消除初始状态对共振峰处响应的影响，仿真时定义扫频初始频率fstart=f0/4（正向扫频）或fstart=4f0（逆向扫频）。

针对f0=20 Hz、ς0=0.02的单自由度系统，分别进行正向（Rexp=2 oct/m in、4 oct/m in）、逆向（Rexp=-2 oct/min、-4 oct/m in）扫频激励下的系统响应计算，结果如图2和图3所示。图2为正向扫频（Rexp=4 oct/min）时，系统响应与激励频率（频率随时间变化）的关系；图3为不同扫频速率下的非稳态振动与稳态振动（Rexp=0）下系统响应的对比。

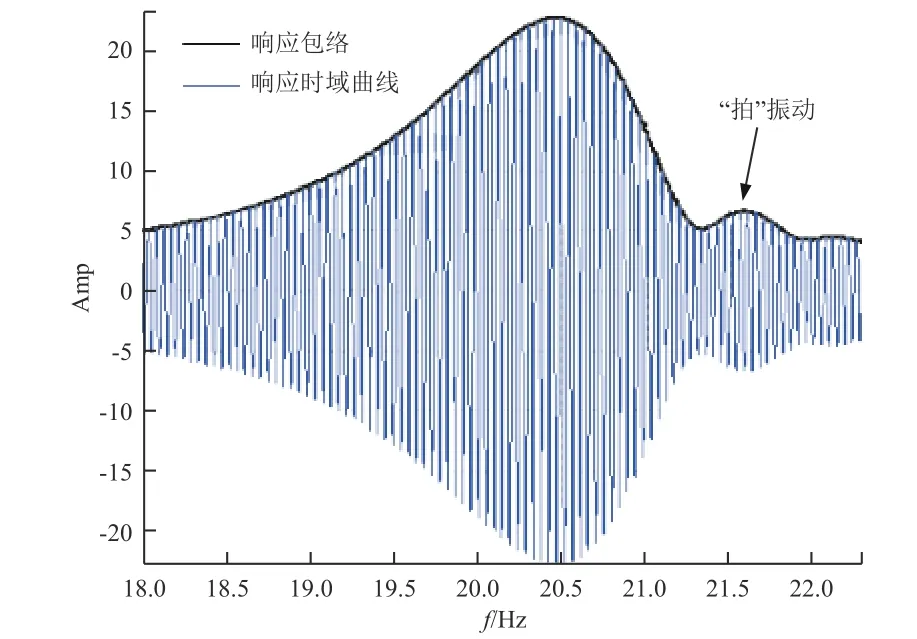
图2 正向扫频（R exp=4 oct/m in）时系统响应与频率关系Fig.2 Response of positive exponential sweep excitation(R exp=4 oct/min)

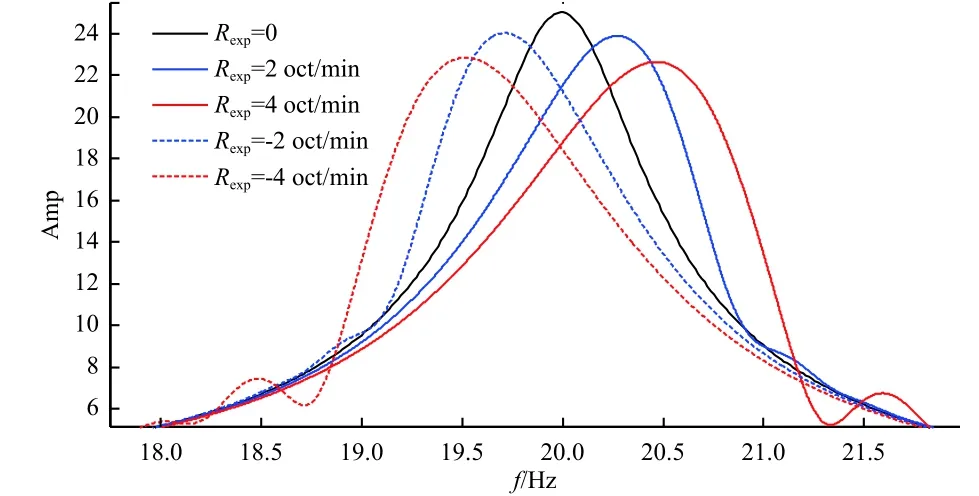
图3 非稳态与稳态振动下的系统响应对比Fig.3 The difference between transient response and steady response at several sweep rates

由图3可知，在正向和逆向扫频激励下，系统响应峰值减小，且共振峰形状扭曲，半功率带宽增大；正向扫频下，峰值频率增加（右移），大于共振频率fmax；逆向扫频下，峰值频率减小（左移），小于共振频率fmax；扫频速率越高，上述特征越明显。另外，在图2中，在响应峰值之后，又出现了一个小的峰值，这是由“拍”振动引起的。此处振动由两部分叠加而成，一部分是系统以共振峰处的振动状态为初始条件作有阻尼自由振动，另一部分是系统在该“拍”振动频率处作受迫振动，两部分振动的频率相近，叠加形成了“拍”振动现象。

2 扫频速率对系统响应影响的定量分析

2.1 共振响应特性

对于f0=20 Hz、ς0=0.05的单自由度系统，其静止初始条件下的共振响应曲线如图4(a)所示。由图可知，系统的响应Amp(t)是随着时间逐渐增大的，经过大约15个循环之后才达到稳态最大值Ampmax（≈10）。若系统不是从静止状态开始（不失一般性，可假定系统初始速度为0，但初始位移与激励的位移幅值之比为αAmpmax，其中α∈(-1,1)），则系统的响应为

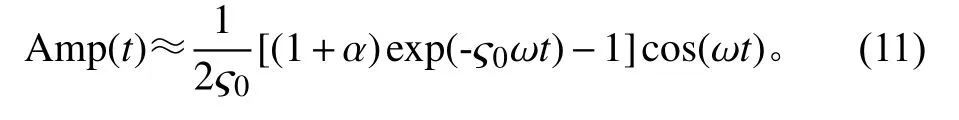
令α=-0.8，系统的共振响应曲线如图4(b)所示。由图可知，系统经过大约9个循环之后即可达到稳态响应。文献[10]指出，系统阻尼比ς0越小，则响应趋于稳定所需的循环周数就越多。因此在正弦扫频振动中，由于激励频率随时间变化，扫频激励在系统共振频率处停留的时间很短、循环次数较少，以致系统响应峰值达不到稳态最大值Ampmax。

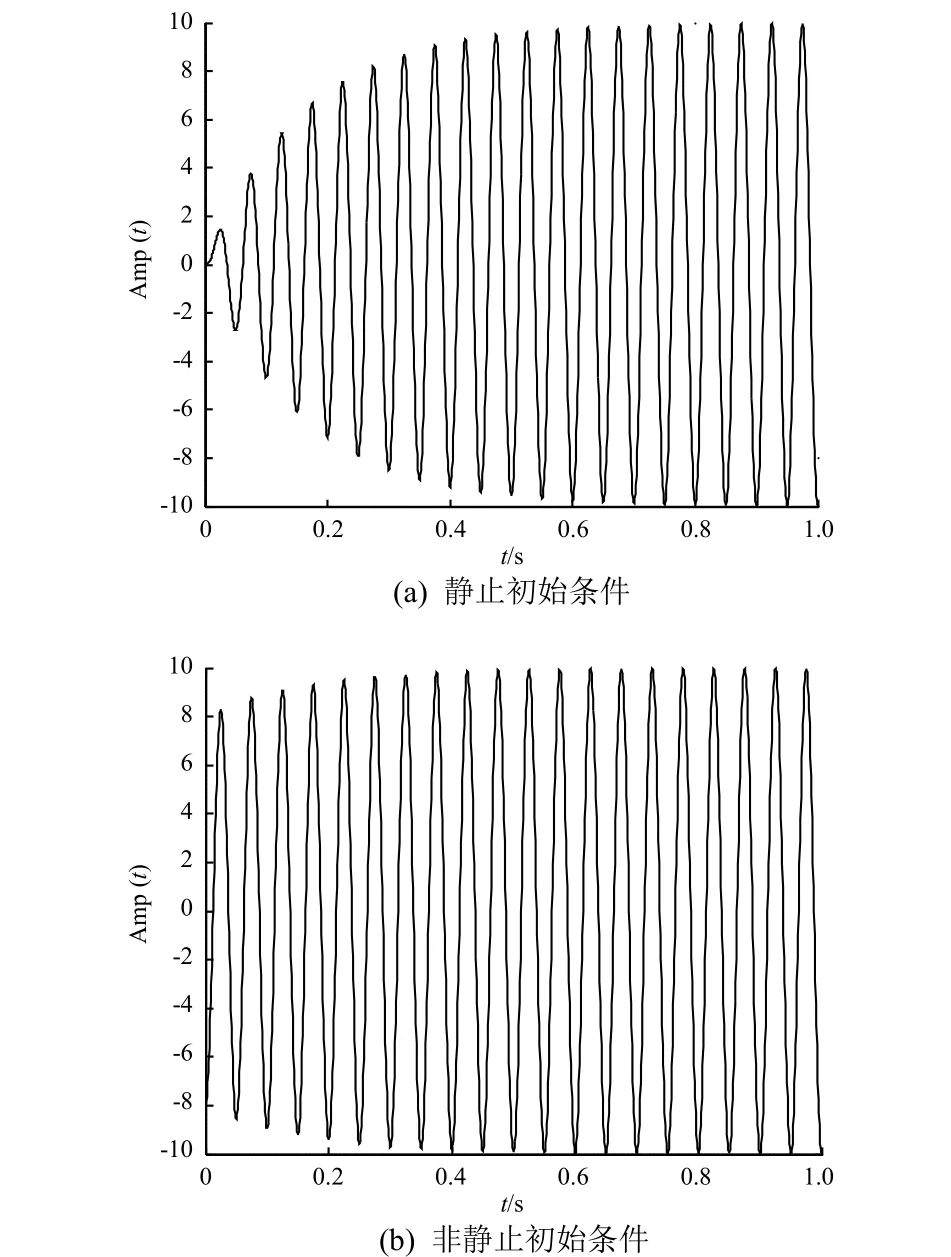
图4 静止和非静止初始条件下的系统共振响应曲线Fig.4 Resonance response curve under static (a)and nonstatic(b)initial conditions

2.2 量纲为1的扫频参数

由式(11)可知，当激励频率等于系统共振频率时，系统响应Amp(t)的值与ς0ωt有关。将ς0ωt改写为

图5 共振频带Fig.5 Resonance bandw idth

对于任何一种既定的正弦扫频模式，β0是确定的，但式(13)中的Δf未定，因此Nr和η无法确定。为此，在系统阻尼比ς0较小的情况下，可令图5中的f1和f2分别为系统半功率带宽的上、下限，则有：

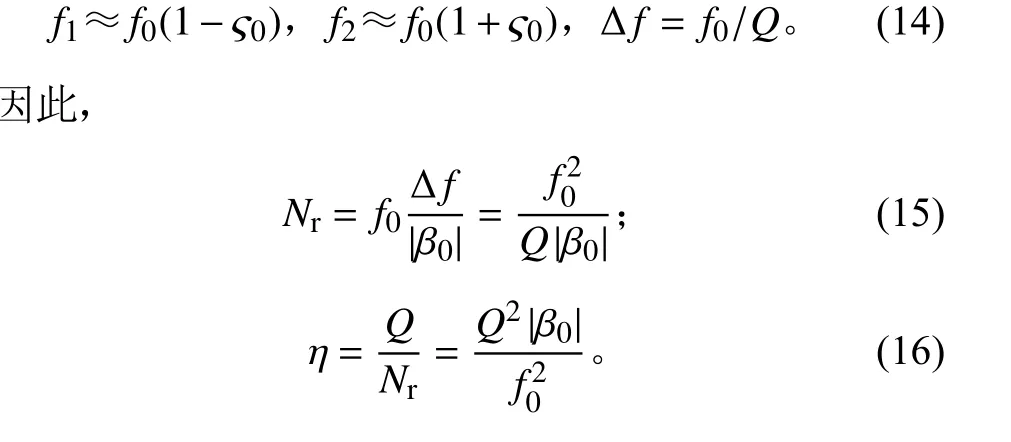
式(15)适用的前提条件是系统阻尼ς0较小、半功率带宽Δf与品质因子Q的关系式Δf=ς0/Q成立、扫频函数f(t)在半功率带宽内单调递增（或递减）且β0≠0。式(16)中的Nr为系统在半功率带宽内的循环次数。此时，对于既定的系统和扫频模式，扫频参数η便可确定。

线性扫频和对数扫频下，η的表达式分别为：

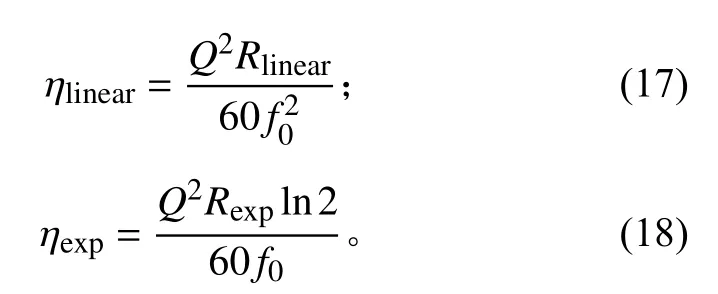
应用MatLab软件对线性和对数扫频下系统的响应特性进行仿真计算。假定系统在扫频激励下的响应最大值为Alinear-max和Aexp-max；η相同但其他参数不同的情况下，Alinear-max/Ampmax和Aexp-max/Ampmax的对比结果详见表1。由表1可知，在扫频参数η相同、其他参数不同的情况下，线性和对数扫频的响应幅值（Alinear-max/Ampmax和Aexp-max/Ampmax）基本是一致的；正向扫频和逆向扫频的响应幅值有微小差异，逆向扫频的结果比正向扫频的大1%～2%；对于正向对数扫频，当Q值（即Rexp/f0的值）相同时，系统响应幅值完全一致；当Q值较小、扫频速率较大（Q=5、Rexp/f0=8）时，响应幅值略有偏差，这是由于ς0=0.1时式(4)的近似关系存在误差，且扫频速率远大于系统频率时，系统响应曲线较稀疏，曲线包络不能准确得到系统响应的最大值，如图6所示。

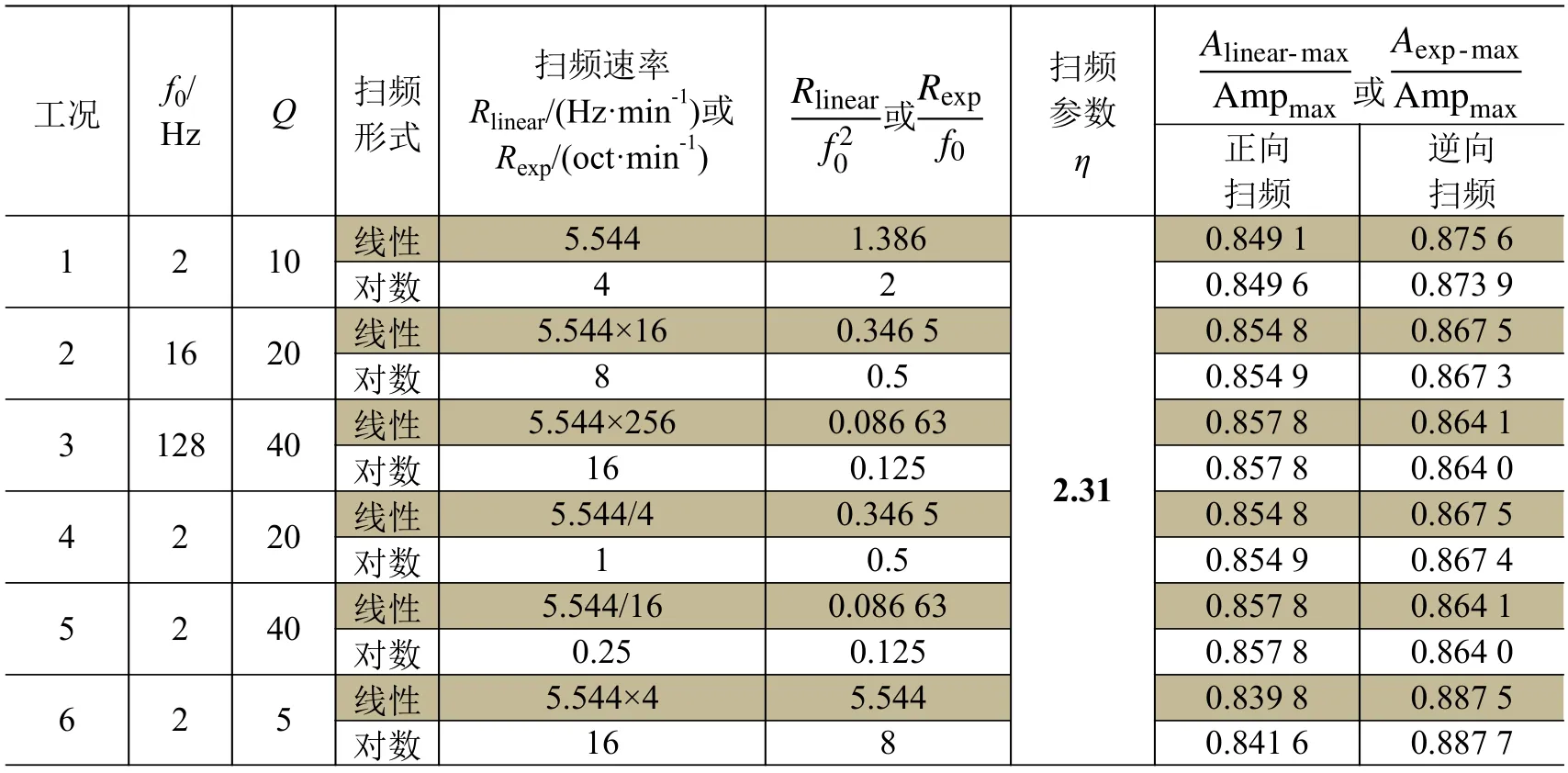
表1 扫频参数η 相同时的线性扫频和对数扫频对比Table 1 Comparison of several responses for sameη(exponential and linear)

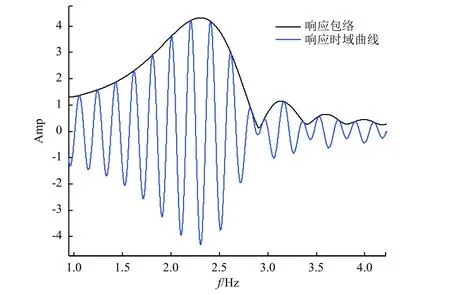
图6 扫频速率远大于系统频率时的系统响应曲线Fig.6 Response curve for very large sweep rate

2.3 扫频参数η 对系统响应的影响分析

由2.2节可知，在扫频参数η相同的情况下系统的响应特性基本一致，但当Rlinear/f02 或Rexp/f0变化时结果略有差别，因此本文仿真计算了Rlinear/f02或Rexp/f0变化对系统响应的影响。Rlinear/f02（或Rexp/f0）取值为0.001～10时，Q分别取值5、10、25、50、100，且正向和逆向扫频都进行仿真；同时，计算了η在0.1～1000间变化对系统响应的影响。文献[4]的研究中令η值在0.1～1000间变化，Rexp/f0恒定为0.1，只改变Q的值。这是不够全面的，因为Rexp/f0的变化对结果有一定影响。因此本文分别将Rexp/f0的取值固定为0.05、0.1、0.5、1、2、5、10（Rlinear/f02 的取值固定为0.01、0.1、0.5、1、2、5、10），通过改变Q的值，使η取值在0.1～1000间变化，然后进行正向和逆向扫频仿真。

图7、图8为系统响应与稳态响应的对比关系：图7为响应峰值与稳态峰值之比；图8为扫频响应的峰值频率的误差，该误差用正则化误差QΔf/fmax表示，其中Δf=|fexp-fmax|或|flinear-fmax|，fexp和flinear分别为对数扫频和线性扫频时的峰值对应频率。由图7、图8可知：随着扫频参数η增大，系统响应峰值减小、峰值频率偏差增大，且系统Q值越大，受影响越明显；正向扫频和逆向扫频的结果差异可以忽略；当引入扫频参数η后，误差曲线基本合为一条曲线；由图7(b)可知，Rlinear/f02或Rexp/f0取不同值对结果的影响基本可忽略，4种扫频类型共28条曲线几乎重叠。

图7 R linear/f02 或R exp/f0 及扫频参数η对系统响应峰值的影响Fig.7 The influence of R linear/f02(or R exp/f0)and ηon the amplitude

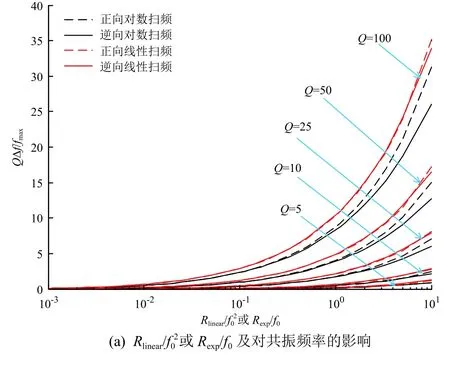
图8 R linear/f02 或R exp/f0 及扫频参数η对共振频率的影响Fig.8 The influence of R linear/f02(or R exp/f0)and ηon the resonance frequency

拟合曲线见图7(b)。

图8(b)中的28 条曲线基本一致，当η超过100时，出现一定偏差，正则化频率误差QΔf/fmax与η的关系为

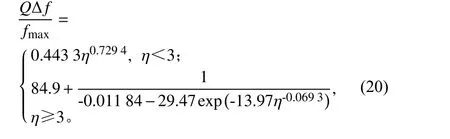
3 多自由度系统的扫频响应验证

文献[11]对受到线性扫频激励的两自由度系统的响应进行了分析，得出“扫频速率越慢，系统响应越趋于稳定响应”的结论，但对响应的误差无定量估算。我们对如图9所示的简化卫星模型进行对数正弦扫频激励，讨论扫频速率对多自由度结构响应的影响。该简化模型尺寸为1m×1m×2 m，横向一阶频率16.4 Hz。在横向1g的稳态激励下，顶点最大响应为18.5g（阻尼比取0.03）。对结构底部施加1g的正弦扫频激励，扫频速率分别为4 oct/min、8 oct/m in、16 oct/m in 时，系统响应峰值和峰值频率如表2所示，表中单自由度模型结果是将扫频参数η代入式(19)、式(20)计算得到的。由表2可知，随扫频速率增大，结构响应峰值降低，峰值频率增大；当扫频速率为8 oct/m in 时，扫频响应峰值与稳态响应的相差达11%；单自由度模型的计算结果与多自由度模型有微小差异，这是由于模态叠加时，高阶模态对此处的响应也有一定贡献。总体来看，当多自由度系统模态稀疏且相邻模态之间影响较小时，拟合公式（式(19)、式(20)）以及图7、图8基本适用于多自由度系统低阶模态处的扫频响应分析。

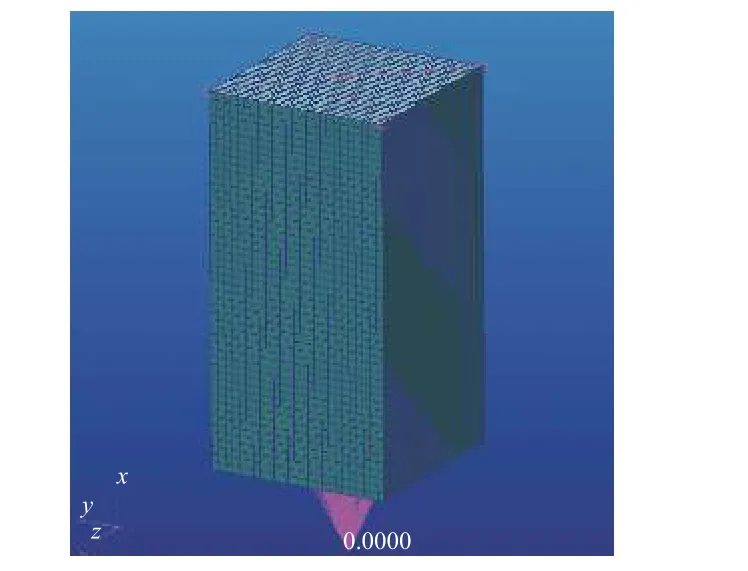
图9 简化卫星模型Fig.9 Simplified FEM model of a satellite

表2 多自由度系统的扫频响应Table2 Responses of a multi-DOFsystem under sine-sweep excitations

4 结论

本文使用数值方法，研究了单自由度系统在正弦扫频激励下的响应特性；通过单自由度系统的共振响应特性，推导了量纲为1的扫频参数η；计算结果表明，参数η对单自由度系统的扫频响应起决定性影响；通过计算得到了扫频响应峰值、峰值频率与参数η的关系曲线及拟合公式；最后使用简化卫星模型，验证了参数η基本适用于多自由度系统的扫频响应分析。

研究得出结论如下：

1）在正弦扫频激励下，系统最大响应减小、正向扫频峰值频率增大（逆向扫频峰值频率减小），且扫频速率越高，影响越明显。

2）线性扫频和对数扫频激励下，系统响应基本一致；正向扫频和逆向扫频激励下，系统响应有微小差异，最大幅值相差1%～2%。

3）在扫频参数η相同，其他参数不同的情况下，系统响应特性基本一致。

4）对于复杂卫星结构（多自由度系统），在低阶模态处、相邻模态之间影响较小时，本文基于单自由度系统得到的拟合公式（式(19)、式(20)）以及图7、图8可用于预示其扫频响应特性。

另外，工程试验人员在正弦振动试验前，可参考本文研究结果，根据试验要求或者需要特定考核的频段，设置合理的扫频速率，既保证扫频时间不会太长，又可使试验结果达到预期的精度；亦可在正弦振动试验后，根据上述公式或图表，对试验得到的响应特性数据进行一定的修正。对于频带较宽的扫频试验，建议针对不同频段分别设置不同的扫频参数，在保证试验精度的同时节省试验时间。例如，对于Q=10、f0=30 Hz 的模态，Rexp/f0=0.1，即Rexp=3 oct/m in 时，扫频响应的误差不足3%；对于Q=10、f0=200Hz 的模态，Rexp=20 oct/m in 时亦可达到相同的精度。