一种线性扫频干扰信号的参数估计方法

2016-12-28姚富强牛英滔

通信技术 2016年12期

关键词：扫频频带参数估计

周新，姚富强，牛英滔

（1.解放军理工大学通信工程学院，江苏南京 210007；2.南京电讯技术研究所，江苏南京 210007）

一种线性扫频干扰信号的参数估计方法

周新1，姚富强2，牛英滔2

（1.解放军理工大学通信工程学院，江苏南京 210007；2.南京电讯技术研究所，江苏南京 210007）

提出一种基于传统周期图功率谱估计的线性扫频干扰信号特征参数估计的新方法。该方法主要利用线性扫频干扰信号瞬时频率随时间线性、周期变化的规律，等间隔截取多段长度相同的数据，并估计出每段数据的中心频率，进而根据中心频率变化趋势，判断截取的多段数据是否跨越一个扫频周期，最后运用等差数列性质，实现扫频速率、扫频周期和扫频带宽的参数估计。仿真结果分析表明，该方法估计精度较高。

通信抗干扰；参数估计；线性扫频信号；功率谱

0 引言

通信干扰[1]已由传统的基于单机信道干扰的狭义干扰发展到基于多维空间干扰的广义干扰。它主要表现在：从固定干扰发展到动态干扰；从压制式干扰发展到压制式和灵巧式干扰相结合等。其中，线性扫频干扰信号是一种典型的动态干扰样式，干扰能量集中、干扰带宽较宽、实施方便，干扰效率高。在一个扫频周期内，线性扫频干扰信号的频率随时间线性变化，也叫线性调频信号。它的主要特征参数包括扫频周期、扫频速率、扫频带宽、瞬时功率等。对其相关特征参数进行精确估计，可为预测扫频干扰行为、研究抗扫频干扰策略提供条件。

目前，部分学者对线性扫频干扰信号特征参数估计算法进行了研究。文献[2]采用周期图功率谱估计方法估计并列举出线性扫频干扰信号多个时刻的所在频率，然后估计出线性扫频干扰信号的起止频率和瞬时功率等参数。该方法虽然以较低复杂度估计出线性扫频干扰信号的起止频率，但其估计误差直接取决于每次分析的时间间隔，估计精度不理想。文献[3]采用STFT得到线性扫描干扰信号的时频等高线图，然后计算各等高区域均值中心点对应坐标值，求出各坐标值之间斜率的平均值，最后得到线性扫描干扰信号的扫描速率，文献[4]采用Chirp-Fourier变换有效估计出加入噪声的线性扫频干扰信号的初始频率和扫频率。文献[5]分析扫频干扰的速率和干扰带宽最小分辨率对FH/MFSK系统误比特率性能的影响。文献[6]依据线性调频信号相位比较稳定这一特征，提出一种基于频域相位方差加权的线性调频信号检测方法，但对于扫频周期和扫频带宽等参数估计没有给出相应的方法。文献[7]采用平滑伪Wigner-Ville分布（SPWVD）的时频分析方法，观察扫频干扰信号的时频特征，再进行统计，平均估计出扫频干扰信号的扫频周期及扫频带宽。然而，此方法需要人为观察并多次记录相关参数值，估计精度难以保证。文献[8]提出了基于STFT和分段式Radon变换的线性扫频信号参数测量方法，在STFT基础上再进行分段式Radon变换，估计出扫频速率、起止频率等参数。文献[9]基于线性调频信号具有近似矩形的幅频特性，对其频谱的差分过程进行处理，采用正交匹配追踪算法，有效提供欠采样信号频谱的边缘信息，实现线性调频信号的起始频率和终止频率的有效估计。文献[10]采用解线调法对LFM信号的调频斜率进行搜索，然后根据估计的调频斜率值对信号进行解线调，估计起始频率。上述方法几乎都假设参数估计过程是在一个扫频周期内完成的，而在具体实现中，扫频干扰信号的周期及其精确起始时刻往往未知。基于这点考虑，本文首先按照等时间间隔截取多段扫频干扰信号，并采用改进周期图法估计其瞬时功率谱；其次，依据设定的门限值提取每段信号的频率范围；再次，取均值估计出中心频率；最后，根据等差数列性质，实现扫频速率、扫频周期及扫频带宽的估计。

1 系统模型

线性扫频干扰信号Jchirp(t)的时域表达式为[10]：

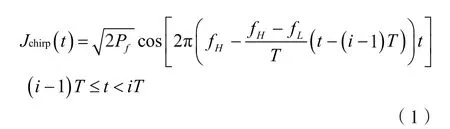
其中，2Pf为干扰功率，T为扫频周期，fH为最高频率，fL为最低频率。它的频率随时间变化的波形如图1所示。

图1 线性扫频干扰信号时频

假设通信接收机接收的线性扫频干扰信号为：

其中Jchirp(t)为线性扫频干扰信号，n(t)为方差等于σ2的高斯白噪声。

对于采样后的数字信号，可表示为：

本文需要解决的问题主要是如何根据通信接收机接收到的J(l)，估计线性扫频干扰的扫频速率、扫频周期和扫频带宽。

为便于研究，作出如下假设：

（1）通信接收机已检测出干扰信号类型为线性扫频干扰；

（2）通信接收机为宽带接收机，其接收带宽超过线性扫频干扰的扫频带宽；

（3）通信接收机的采样速率满足无失真接收扫频干扰信号的奈奎斯特采样要求；

（4）通信接收机对扫频干扰瞬时功率谱估计一次所需的时间（即检测周期）远小于扫频干扰周期；

（5）通信接收机截取扫频干扰的时间间隔小于扫频干扰周期的1/3。

2 算法描述

在一个周期内，线性扫频干扰信号的频率随时间变化单调递增或递减。实际检测中，假设通信接收机每隔时间tΔ（tΔ小于扫频干扰周期）对接收到的采样数据进行一次功率谱估计，每次估计的数据长度为L，其中0≤l≤L-1。采用改进周期图法，第i次估计得到的功率谱为[11]：

其中wl为窗函数，Fs为抽样频率，L为功率谱点数。本文选用汉明窗。

当截取的次数N超过一定值时，N个时刻将跨越一个扫频周期，即t1、t2、…、tε-1时刻在同一个扫频周期内，而tε、tε+1、…、tN时刻在下一个扫频周期内。本文针对此种情况，估计线性扫频干扰信号的扫频速率K、扫频周期T和扫频带宽H。

算法共分三个步骤。

第一步，估计出线性扫频干扰信号各个时刻ti（i=1,2,3,…,N）的中心频率fi（i=1,2,3,…,N）。首先，分别在各个时刻截取干扰信号进行改进周期图功率谱估计；然后，分别将估计值Pi(f)（i=1,2,3,…,N）进行二值化处理。设α为判决门限，高于门限α的数据设为1，低于门限α的数据设为0，即：

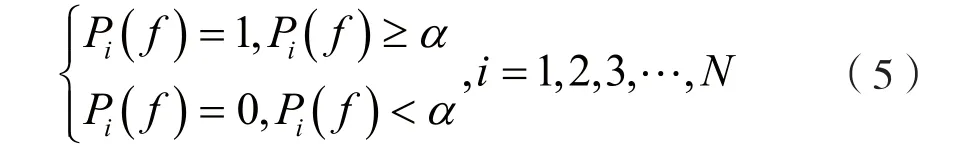
最后，分别提取Pi(f)=1所对应的频率范围，并取其均值为各个时刻的中心频率估计值fi（i=1,2,3,…,N）。

第二步，根据各时刻中心频率估计值的变化趋势，判断这多个截取时刻是否跨越一个扫频周期。如果N个时刻中心频率估计值的变化趋势不是单调变化，即f1＜f2…＜fi-1＞fi＜fi+1…＜fN（i≥2）或f1＞f2…＞fi-1＜fi＞fi+1…＞fN（i≥2），则判断N个截取时刻跨越了一个扫频周期。然后，再进一步判断N是否大于等于4（扫频速率应等于同一扫频周期内相邻两个时刻的中心频率之差除以tΔ，但受噪声及门限值α的影响，其中心频率估计存在一定误差，取多个相邻时刻间的扫频速率均值作为最终速率估计值能提高估计精度，所以取N≥4）。如果是，停止截取线性扫频干扰信号并开始第三步计算；否则，继续等间隔截取干扰信号进行中心频率估计，并按照上述步骤进行判断。

第三步，先根据等差数列性质估计扫频速率K，进而估计扫频周期T，最后估计扫频带宽H。取多个相邻时刻间的扫频速率均值作为最终速率估计值k°，其表达式如下：

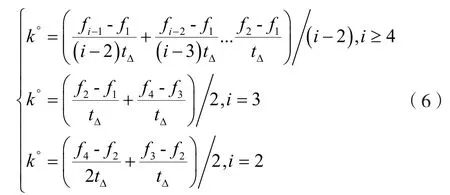
两个线性扫频周期中，瞬时频率值相同的两个时刻的间隔等于扫频周期。所以，可以求出扫频周期估计值T°，表达式如下：

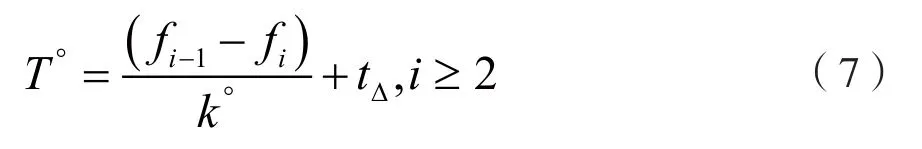
其中，fi-1对应的时刻ti-1与fi对应的时刻ti是相邻且分布在不同扫频周期内的。当k°取正值时，表明线性扫频干扰信号的频率随时间单调递增；当k°取负值时，表明单调递减。所以，扫频带宽估计值L°的表达式如下：

3 仿真分析

3.1 二值化门限的确定

从以上描述可以看出，门限α的取值对估计性能有较大影响。而在复杂电磁干扰环境中，难以实现干扰噪声功率比检测，进而影响了门限α值的精确确定。因此，采用仿真的方法来确定最佳门限值。仿真中，设置接收机采样速率fs为1 MHz/s，扫频干扰信号的起始频率为10 kHz/s，终止频率为250 kHz/s，分别设定干噪比为15 dB、5 dB和-5 dB，取门限值为瞬时功率谱最大模值的74%～90%，进行1 000次运算求平均，分别对扫频信号的扫频周期进行估计，扫频周期的圴方误差如图2所示。

图2 不同门限值扫频周期估计的均方误差

从图2可以看出，当门限值α取75%～78%时，三种干噪比条件下，扫频周期估计均方误差均小于4×10-5。基于上述仿真分析，本文设瞬时功率谱最大模值的77%为门限值。

3.2 相关参数的估计

取N=4进行仿真分析，即对线性扫频干扰信号截取的四个时刻已经跨越了一个扫频周期。另假设该干扰信号的频率在一个周期内随时间是单调递增的，则其瞬时功率谱图如图3所示。

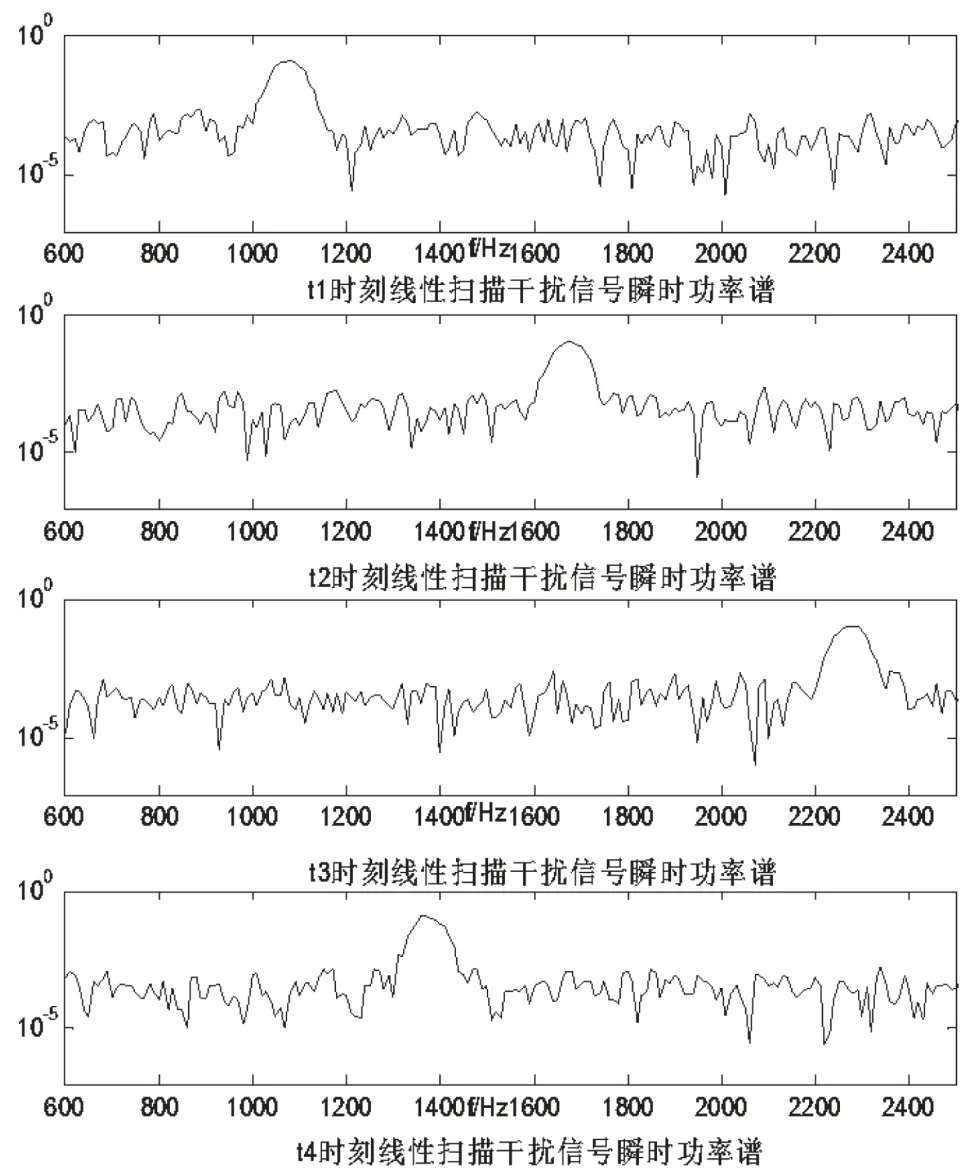
图3 线性扫频干扰信号各时刻瞬时功率谱

通过二值化处理得到各个时刻二值化功率谱，如图4所示。提取每个时刻的频带范围，然后求其均值，得到瞬时中心频率f1、f2、f3、f4。其中，t1、t2、t3、t4四个时刻的分布共有三种情况：

图4 二值化瞬时功率谱值

第一种情况如图5所示，即t1、t2、t3在一个扫频周期，t4在下一个扫频周期。

图5 截取时刻分布

第二种情况如图6所示，即t1、t2在一个扫频周期，t3、t4在下一个扫频周期。

图6 截取时刻分布

第三种情况如图7所示，即t1在一个扫频周期，t2、t3、t4在下一个扫频周期。

图7 截取时刻分布

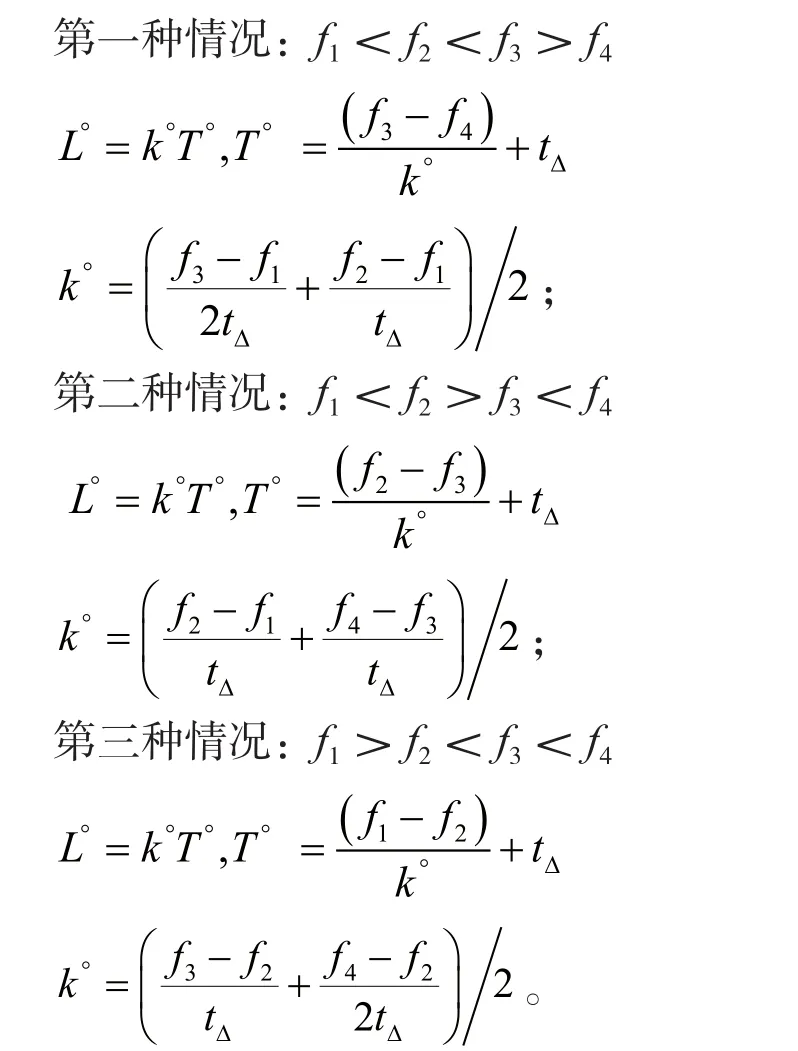
仿真中，设置接收机采样速率fs为10 MHz，门限值设为每段数据最高瞬时功率谱幅值的77%。

由图8可以看出，在-5 dB的低干噪比条件下，三种扫频速率的估计相对误差均低于10-2；随着干噪比的增加，相对误差不断减小；扫频速率快的较扫频速率慢的估计，相对误差要高一些，因为被截取的长度相同的一段数据中，扫频速率快的，其带宽更宽，对中心频率的估计误差影响会更大，进而影响到扫频速率的估计误差。

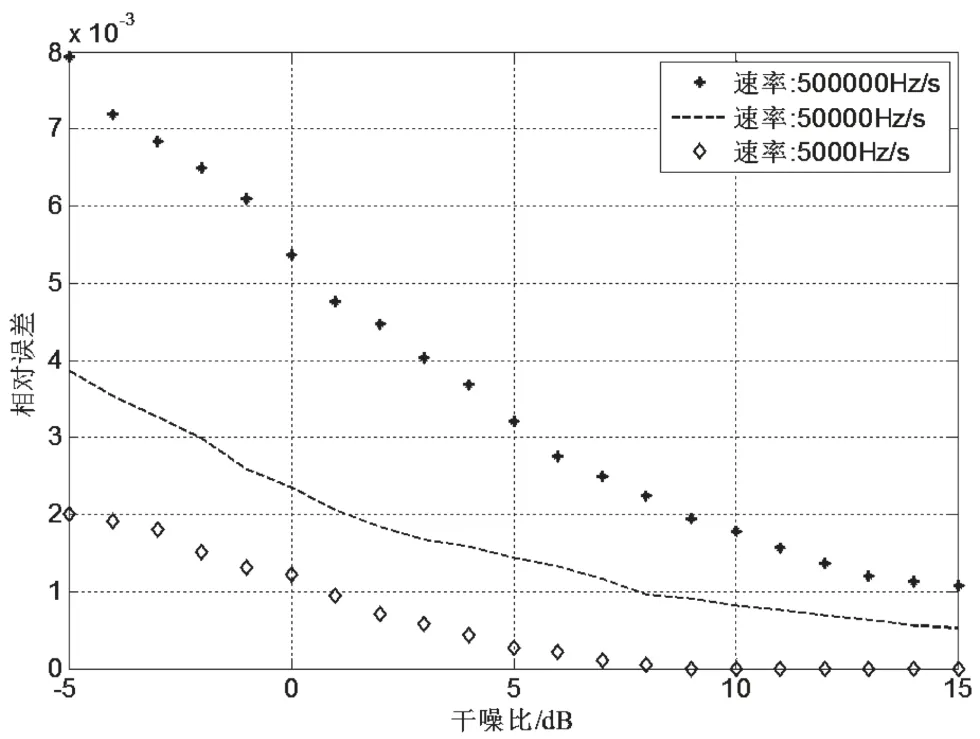
图8 扫频速率估计误差与干噪比的关系

由图9可以看出，在-5 dB的低干噪比条件下，三种扫频周期的估计相对误差均低于8×10-3；随着干噪比的增加，相对误差不断减小。其中，扫频周期为0.01 s的扫频干扰信号，当干噪比大于5 dB时，其扫频周期估计误差趋近于零。

图9 扫频周期估计误差与干噪比的关系

由图10可以看出，在-5 dB的低干噪比条件下，三种扫频带宽的估计相对误差均低于7×10-3；随着干噪比的增加，相对误差不断减小；扫频带宽宽的较扫频带宽窄的估计，相对误差要高一些，因为被截取的长度相同的一段数据中，其带宽宽，对中心频率的估计误差影响会更大，进而影响到扫频带宽的估计误差。

图10 扫频带宽估计误差与干噪比的关系

4 结语

扫频干扰信号是典型的动态干扰信号，对扫频干扰的相关参数进行有效估计，预测其扫频规律，是进行抗扫频干扰策略研究的重要前提和基础。本文采用传统周期图功率谱估计方法，对干扰信号进行等间隔瞬时功率谱估计，按照设定的门限值提取每段信号的频率范围，然后取均值估计瞬时中心频率，最后根据等差数列性质，实现线性扫频干扰信号相关参数的估计。通过仿真分析发现，本文方案估计相关参数的相对误差较小。

参考文献：

[1] 姚富强.通信抗干扰工程与实践[M].第2版.北京:电子工业出版社,2012:4-5. YAO Fu-qiang.Anti Interference Engineering and Practice of Communication[ M].2 edition.Beijing:Publishing House of Electronics Industry,2012:4-5.

[2] JI H C,NING Z,LIN S.A Fast Algorithm for the Chirp Rate Estimation[M].Harbin:Research Institute of Electronic Engineering,Harbin Institute of Technology(HIT),2008:32-36.

[3] 熊建明,李永贵,牛英滔.线性扫描干扰信号的扫描速率估计[J].山西电子技术,2010(06):57-58. XIONG Jian-ming,LI Yong-gui,NIU Ying-tao.The Frequency Sweeping Rate Estimation of the Linear Chirp Signal[J]. Shanxi Electronic Technology,2010(06):57-58.

[4] 齐林,穆晓敏,朱春华.DSSS系统中基于Chirp-Fourier变换的扫频干扰抑制算法[J].电讯技术,2004,16(03): 35-38. QI Lin,MU Xiao-min,ZHU Chun-hua.Frequency Sweeping Interference Suppressing in DSSS System Using Chirp-Fourier Transform[J].Telecommunicationa Technology,2004,16(03):35-38.

[5] 董彬虹,杜洋,周兰林.宽带扫频干扰下FH/MFSK系统性能分析[J].电子科技大学学报,2014,43(05):78-81. DONG Bin-hong,DU Yang,ZHOU Lan-lin.Performance Analysis of Broadband Frequency Sweeping Jamming for FH/MFSK Systems[J].Journal of University of Electronic Science and Technology of China,2014,43(05):78-81.

[6] 王思秀,郭文强,汤建国.基于频域相位方差加权的线性调频信号检测方法[J].计算机应用,2015,35(12):3352-3356. WANG Si-xiu,GUO Wen-qiang,TANG Jian-guo.Detection Method of Linear Frequency Modulated Signal based on Frequency Domain Phase Variance Weighting[J].Journal of Computer Applications,2015,35(12):3352-3356.

[7] 周利华,常琪.一种扫频干扰信号参数估计方法[J].电子设计工程,2015,23(11):675-679. ZHOU Li-hua,CHANG Qi.A Parameter Estimation Method of Sweep Frequency Jamming Signal[J].Electronic Design Engineering,2015,23(11):675-679.

[8] 段宇.低信噪比下的线性调频信号检测与参数估计方法研究[D].长沙:国防科学技术大学,2013:42-45. DUAN Yu.Research on Detection and Parameter Estimation of LFM Signals in Low SNR[D].Changsha:National University of Defense Technology,2013:42-45.

[9] 马宁,王建新,董宁斐.基于正交匹配追踪的欠采样LFM信号参数估计[J].电子与信息学报,2013,35(08):375-381. MA Ning,WANG Jian-xin,DONG Ning-fei.Parameter Esti mation of Sub-sampling LFM Signal based on Orthogonal Matching Pursuit[J].Journal of Electronics & Information Technology,2013,35(08):375-381.

[10] 雷磊.基于时频分析的线性调频信号检测与参数估计[D].西安:西安电子科技大学,2012:29-35. LEI Lei.Detection and Parameters Estimation of LFM Signal based on Time-Frequency Analysis[D].Xian:Xian University of Electronic Science and Technology,2012:29-35.

[11] 吴昊,张杭,路威.一种面向卫星频谱监测的复合式干扰自动识别算法[J].系统仿真学报，2008,20(17):57-60. WU Hao,ZHANG Hang,LU Wei.Algorithm for Compound Jamming Auto-recognition based on Inspecting Spectrum of Satellite Communication[J].Journal of System Simulation,2008,20(17):57-60.

[12] XIAN D Z.Modern Signal Processing[M].Beijing:Tsinghua University Press,2002:92-93.

Parameter Estimation of Linear Chirp Signal

ZHOU Xin1, YAO Fu-qiang2, NIU Ying-tao2
1.College of Communications Engineering, PLA Univ. of Sci. & Tech., Nanjing Jiangsu 210007, China; 2.Nanjing Telecommunication Technology Institute, Nanjing Jiangsu 210007, China)

A new method for parameter estimation of linear chirp signal based on periodogram spectrum estimation is proposed. According to the feature that the instantaneous frequency of the linear chirp signal changes linearly and periodically along with the time variety, many pieces of the same length data with equal time intervals are captured, and the center frequency of each piece is estimated. And then in line with the variation tendency of all the center frequency, whether or not those pieces cross a frequency sweep cycle is judged. Finally, based on the arithmetic progression, the frequency sweeping rate, cycle and bandwidth of the linear chirp signal are calculated. Simulation indicates that the proposed method could achieve fairly high estimation precision.

anti-jamming communication; parameter estimation; linear chirp signal; power spectrum