干湿交替对砂岩断裂特性影响试验研究

2022-01-13董世明淦志强

西南石油大学学报(自然科学版) 2021年6期

董世明，淦志强，华文

1.深地科学与工程教育部重点实验室·四川大学，四川成都 610065

2.破坏力学与工程防灾减灾四川省重点实验室·四川大学，四川成都 610065

引言

在库岸边坡、坝基、采矿和隧道开挖等众多工程领域中，岩石的变形破坏常常伴有水的参与，水-岩相互作用被认为是影响岩土工程安全稳定性的一个重要因素[1-2]。同时，很多地质灾害（如滑坡、泥石流等）的成因与防治[3]、文化遗产（如石窟、岩画等）的损毁[4]均与水-岩相互作用紧密相关。由于自然界环境的更替和人为因素的参与（如水库的防汛和发电等），地表和地下水水位均表现出季节性变化，使得库岸边坡等岩体工程往往处于干湿交替的状态[5-6]。

这种周期性的水-岩相互作用势必会对岩体的物理力学性能造成一定的影响。通过已有的研究发现，周期性的干湿交替作用对岩石力学性能及岩体工程稳定性的弱化作用都要比长时间浸水作用要强很多[7-8]。

近年来，国内外学者针对干湿交替作用下岩石类材料的物理力学性能开展了大量的研究工作[9-17]。他们关注的这些物理性能参数主要包括：质量、密度、吸水率、孔隙率、P 波波速等；而力学性能参数主要有：抗拉强度、单轴抗压强度，三轴抗压强度、黏聚力、内摩擦角、抗剪强度、弹性模量等。研究结果表明：干湿交替作用后岩石的物理力学性能均发生不同程度的弱化，其弱化程度与岩石的岩性、干湿交替次数、浸泡溶液等密切相关。

此外，目前有关水-岩作用对岩石断裂特性影响的研究主要集中于不同溶液短期（或长期）浸泡后岩石的纯I 型断裂韧度[18-20]。虽然朱敏等[8]和韩铁林等[21]研究了干湿交替作用对岩石纯I 型断裂韧度的影响，然而，有关干湿交替作用下岩石纯II型以及I～II 复合型断裂特性的研究仍然较少[22-23]。由于岩石结构的复杂性，其内部微裂纹的分布较为随机，且在外部复杂荷载作用下，岩石的断裂破坏大都呈现为I～II 复合型断裂破坏模式[24]。因此，开展干湿交替作用下岩石I～II 复合型断裂特性研究十分必要。

基于此，本文拟利用中心裂纹圆盘试件开展砂岩I～II 复合型断裂试验，研究干湿交替作用对砂岩纯I 型、纯II 型和I～II 复合型断裂韧度以及裂纹扩展规律的影响，并结合断裂准则对试验结果进行分析和讨论，以期为岩土工程安全稳定性分析提供必要的理论依据。

1 试验方法及过程

1.1 中心裂纹圆盘试件的应力强度因子

中心裂纹圆盘试件因其构型简单，试件加工方便，仅需改变裂纹面与加载方向的夹角（加载角），便可实现完整的纯I 型、纯II 型以及I～II 复合型加载方式，并且其应力强度因子存在解析公式[25]，因而被广泛地用于脆性或准脆性材料断裂韧度的测量。如图1 所示，半径为R，厚度为t，裂纹长度为2a 的中心裂纹圆盘试件在径向承受集中荷载P 的作用，裂纹面与荷载P 的夹角（加载角）为β。Dong等[25]利用权函数理论推导出了中心裂纹圆盘试件应力强度因子

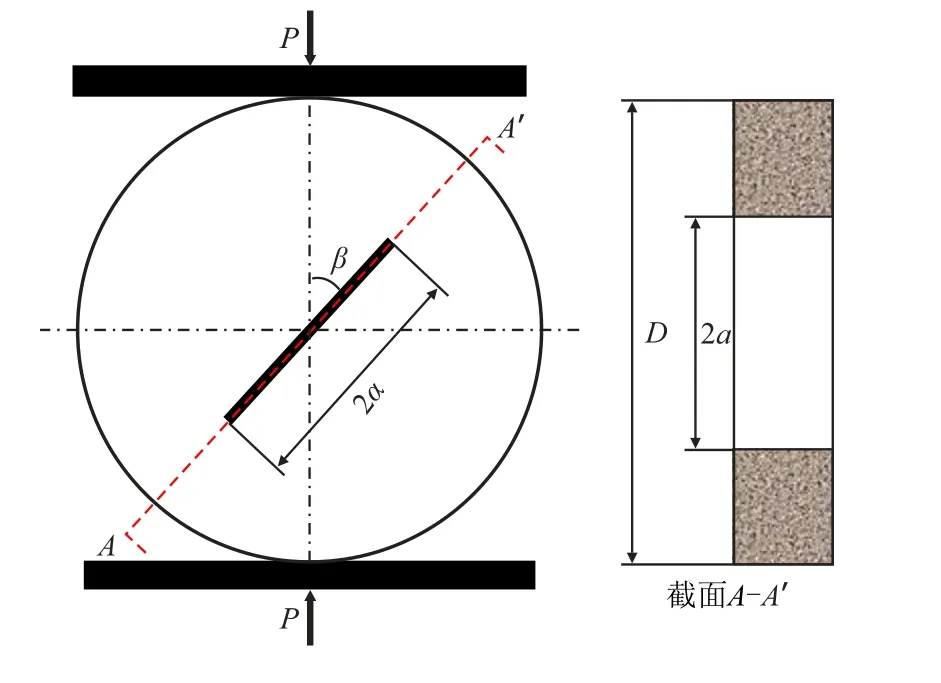
图1 中心裂纹圆盘试件受力示意图Fig.1 Diagram of the central cracked Brazilian disk specimen under compression

无因次应力强度因子YI和YII可表示为

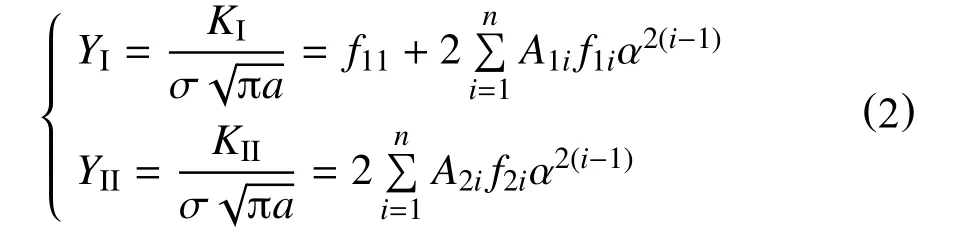
1.2 试验过程

本次试验选用均质性较好的砂岩作为研究对象，为了尽量避免因岩样的个体差异所引起的试验误差，所有试件均取自同一块颗粒细致紧密，均匀性较好的青砂岩试样。试验测得此种青砂岩的干密度为2.24 g/cm3，含水率为1.20%，吸水率为6.18%，泊松比为0.21，抗拉强度为2.67 MPa。通过XRD 分析表明，其矿物成分主要包括石英，斜绿泥石，钠长石和基性磷铝石[26]。此次试验选用的中心裂纹圆盘试件的直径D=75 mm，厚度t=25 mm，相对裂纹长度α=0.5，槽宽约为1 mm。中心裂纹圆盘试件的详细加工过程可参考文献[22]，加工过程中对所有试件进行筛选，剔除差异性较大的试样。

为了模拟“饱水-干燥”周期性的水-岩作用，参照前人的研究方法[12，17]，定义一次完整的干湿交替过程为：将加工好的砂岩试件放入浸泡缸中自然饱水48 h，而后将其放入105°C烘箱中烘干24 h，然后取出自然冷却至于常温。在室内对砂岩试件分别进行1 次、3 次、5 次和7 次干湿交替作用，将经过设定干湿循环次数的砂岩试件再饱水48 h 后进行断裂试验。对于未经处理的天然试件定义为经0次干湿交替作用的试件。

为实现不同类型的断裂形式，此次试验共设计了4 种不同的加载角，即：0°（纯I 型），10°，15°和23°（纯II 型）。试验在四川大学破坏力学与工程防灾减灾四川省重点实验室进行，采用电子万能材料试验机进行加载，加载方式采用位移加载控制，加载速率为0.05 mm/min。每组试验至少包括了4 个试样；对于每个试件，均加载至裂纹扩展破坏，记录下完整的载荷-位移曲线。部分典型砂岩试件破坏形态如图2 所示。

图2 部分典型砂岩试样的破坏形态图Fig.2 The failure modes of typical sandstone specimens

2 试验结果及分析

2.1 干湿交替对砂岩断裂韧度的影响

将试验测得的最大荷载代入中心裂纹圆盘试件的应力强度因子公式即可计算出不同条件下砂岩的临界应力强度因子值（断裂韧度）。不同干湿交替次数后砂岩的纯I 型、纯II 型以及I～II 复合型断裂韧度试验结果列于表1 中。

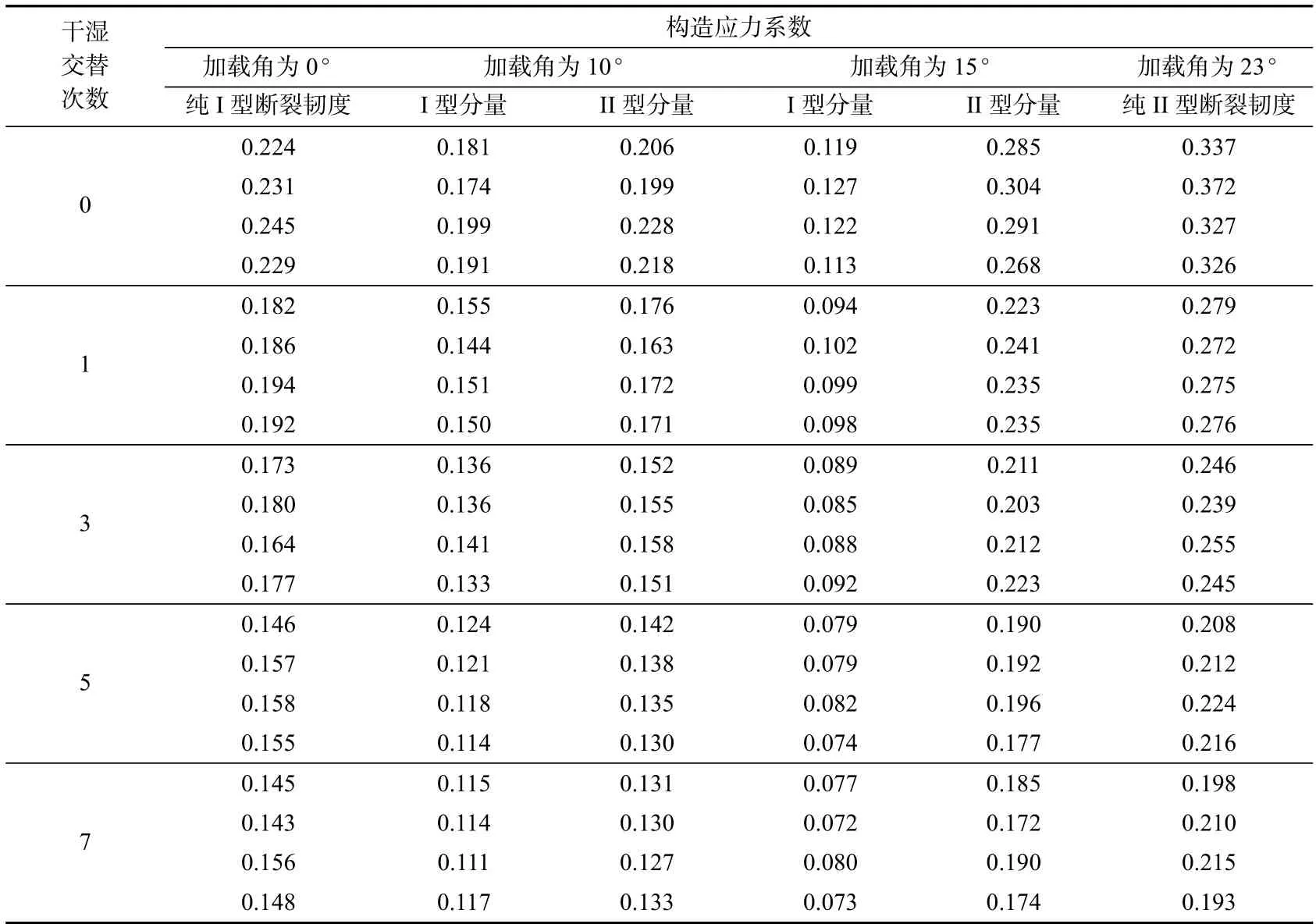
表1 砂岩断裂韧度试验结果Tab.1 The test results of sandstone specimens

如表1 所示，干湿交替次数分别为0、1、3、5 和7 时的纯I 型断裂韧度分别为0.232，0.189，0.173，0.154 和0.148 MPa·m0.5；而相应的纯II 型断裂韧度分别为0.341，0.275，0.246，0.215 和0.204 MPa·m0.5。

干湿交替次数相同时，纯II 型断裂韧度总是比纯I 型断裂韧度要大，这与大多数研究者采用中心裂纹圆盘试件所得的结果类似[22]。

砂岩的纯I 型、纯II 型断裂韧度均随着干湿交替循环次数的增加而减小。与天然砂岩试件相比，当干湿交替循环次数分别为1，3，5 和7 时，纯I 型断裂韧度分别降低了18.5%，25.4%，33.6%和36.2%；而纯II 型断裂韧度分别减小了19.4%，27.9%，37.0%和40.2%，纯II 型断裂韧度的降低幅度（劣化度）约为纯I 型断裂韧度的1.1 倍。

由此可见，纯II 型断裂韧度比纯I 型断裂韧度对干湿交替劣化作用更为敏感。

此外，当干湿交替次数分别为0，1，3，5 和7时，纯II 型断裂韧度与纯I 型断裂韧度的比值分别为1.470，1.455，1.422，1.396 和1.378；可见，纯II 型断裂韧度与纯I 型断裂韧度的比值也随着干湿交替循环次数的增加而呈现出略微减小的趋势。

当I～II 复合型加载时，无论加载角β 为10°还是15°，砂岩的临界应力强度因子的II 型分量KIIf总是大于I 型分量KIf，这主要是因为两种加载条件下中心裂纹圆盘试件的无量纲II 型分量的值总是大于I 型分量。

当加载角为15°，干湿交替次数为0，1，3，5 和7 次时砂岩临界应力强度因子的I 型分量分别为0.120，0.098，0.089，0.079 和0.076 MPa·m0.5；而相应的II 型分量分别为0.287，0.233，0.212，0.189 和0.180 MPa·m0.5。

砂岩断裂韧度的I、II 型分量均随着干湿交替次数的增加而减小；与天然的砂岩试件相比，当干湿交替次数达到7 次时，其I，II 型分量分别减小了36.7%和37.3%。

可见，干湿交替作用对砂岩I～II 复合型断裂韧度也有较大的影响。此外，当加载角为10°时也可得到相同的结论。

为了更为直观的描述I～II 复合型加载时砂岩复合型断裂韧度的变化规律，我们引入等效断裂韧度Keff的概念，其定义式如下

根据表1 和式（3）计算得到的等效断裂韧度的平均值如图3 所示。

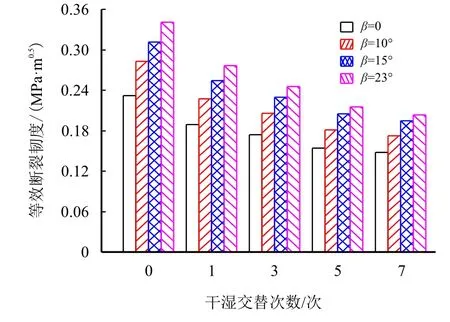
图3 不同干湿交替次数时砂岩的等效断裂韧度Fig.3 The effective fracture toughness of sandstone after different numbers of wetting-drying cycles

当加载角为10°时，干湿交替循环次数分别为0，1，3，5 和7 时的等效断裂韧度分别为0.283，0.227，0.206，0.181 和0.173 MPa·m0.5。

与天然试件相比，等效断裂韧度分别降低了19.8%，27.2%，36.0%和38.9%。

然而，当加载角为15°时，干湿交替循环次数分别为0，1，3，5 和7 时的等效断裂韧度分别为0.311，0.254，0.230，0.205 和0.195 MPa·m0.5。

与天然试件相比，等效断裂韧度分别降低了18.3%，26.0%，34.1%和37.3%。

当干湿交替次数为7 次时，砂岩的等效断裂韧度从纯I 型到纯II 型分别降低了36.2%，38.9%，37.3%和40.2%。可见，纯I 型时的劣化度总是小于纯II 型以及I～II 复合型时的情形；对于其他干湿交替次数（如：1，3，5）时，也可得到相同的结果。

因此，可得到这样的结论：当加载角较大或II型分量占主导时，干湿交替劣化作用对砂岩断裂韧度的影响更为显著。

2.2 干湿交替作用的劣化机理分析

岩石是由多种矿物晶粒、胶结物和孔隙组成的结构较为复杂的聚合物，其力学性能与其矿物成分以及微观结构密切相关[24]。

为了探究干湿交替作用的劣化机理，利用扫描电子显微镜（SEM）观测了天然试件和经7 次干湿交替作用后试件的表面微观形貌，其结果如图4 所示。从图4a 可以看出，天然的砂岩试样中存在少量的间隙、孔洞以及微裂纹，这为水-岩之间相互作用创造了条件。

图4 干湿交替作用后砂岩表面形貌图Fig.4 SEM photomicrographs of the surfaces of sandstone after wetting-drying cycles

浸泡时，大量的水溶液通过孔隙、微裂纹和矿物颗粒间的接触面向岩体内部渗透，水溶液进入岩体矿物颗粒间隙后与其内部的活性矿物发生物理或化学反应；同时，水作为一种溶剂，可以溶解一些可溶性的矿物质，这都将导致矿物颗粒间的黏结力减弱。此次试验用的砂岩试件的矿物成分主要包括石英，斜绿泥石，钠长石和基性磷铝石，其中，斜绿泥岩是最容易被溶解的[26]。

在浸泡过程中，水溶液与组成砂岩的矿物质发生溶解、溶蚀等物理、化学反应，导致矿物颗粒间的黏结程度降低，孔隙率增加，使得砂岩的微观结构发生了改变。

加热干燥时，砂岩中的水分子被加热蒸发，热的水分子会将溶于其中的可溶性矿物质带出到砂岩表面，导致孔隙率增大。

另一方面，砂岩是由多种矿物成分组成的，对于不同的矿物质，其热膨胀系数各不相同，在“加热-冷却”过程中，矿物颗粒之间会发生膨胀或收缩，从而导致矿物颗粒接触面相互挤压，这个过程将会使之前存在的微裂纹扩展，或者产生新的二次裂纹[22-23，26]。

Hale 等[12]指出，岩石中水分子的存在是“加热-冷却”劣化作用发生的先决条件。每次干湿交替循环时，在加热干燥前，由于砂岩试样先进行饱水处理，因此其内部含有大量的水分，这将进一步加强“加热-冷却”劣化作用的发生。

随着干湿交替循环次数的增加，水-岩作用越来越显著，水侵蚀到的岩石颗粒逐渐增多，矿物颗粒间的微裂纹数量和尺寸均逐渐增多（图4b），导致矿物颗粒间的黏结力进一步降低，孔隙率（或吸水率）增大。孔隙率的增加使得每次循环后水的侵蚀程度加深，岩体中的含水量越多，进一步促使“加热-冷却”劣化作用的发生，进而使得砂岩宏观力学性能的降低。

总而言之，干湿交替作用是一个损伤累积并扩大发展直至破坏的渐变过程。在干湿交替过程中，组成砂岩的矿物质会与水溶液发生溶解、溶蚀等物理、化学反应，导致可溶性的矿物质被溶解，颗粒间的黏结力减小，同时使得岩体中的微裂纹扩展，或者产生新的二次裂纹。这个过程改变了砂岩的微观结构，随着干湿交替次数的增加，对应的物理、化学损伤不断累积，进一步加大了其微观结构的变化程度，在宏观上体现为其抵抗裂纹扩展能力的降低。

3 基于复合型断裂准则的理论分析

Hua 等[27]在传统最大周向应变（MTSN）准则的基础上，考虑了T应力的影响，提出了广义最大周向应变（GMTSN）准则。根据广义最大周向应变准则[27]，裂纹沿最大周向应变的方向起裂（θ0），并且当该方向的周向应变εθθ达到某一临界值εt时，裂纹发生失稳扩展。因此，广义最大周向应变准则可表示为

而裂纹尖端的周向应变εθθ可表示为[27]

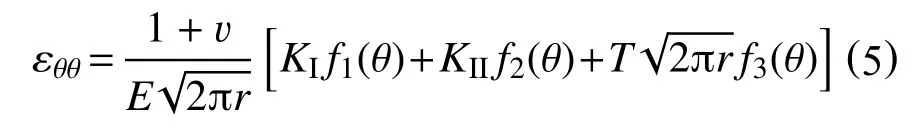
上式中，系数f1，f2和f3的表达式为

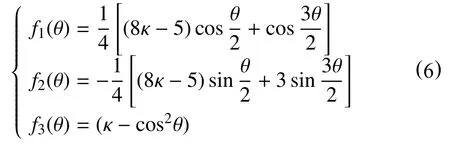
将式（5）代入式（4）即可得到计算裂纹开裂角θ0的表达式

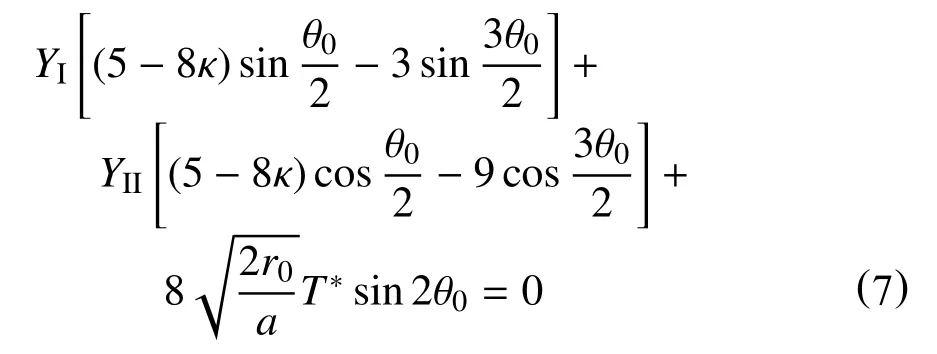
同样地，根据广义最大周向应变准则，KIf/KIC和KIIf/KIC的比值可表示为[27]

需要说明的是，这里的和YI0分别表示纯I型加载时的无量纲T 应力和I 型应力强度因子。

对于中心裂纹圆盘试件而言，其T 应力的解析表达式已由Hua 等[28-29]给出。根据本文的试验条件，相对裂纹长度为0.5，加载角分别为0、10°、15°、23°时，无量纲T应力分别为5.790、4.634、3.465 和1.483[28]。如果参数ν，YI，YII，T*，r0均已知，就可以用式（7）计算裂纹开裂角θ0，并利用式（8）和式（9）计算I～II 复合型加载条件下的断裂韧度比值KIf/KIC和KIIf/KIC。

此外，如果忽略泊松比的影响，广义最大周向应变准则将退化为广义最大周向应力准则[27]。

为了利用广义最大周向应变准则，需要知道另一个参数r0的数值。对于岩石等大多数脆性或准脆性材料，临界距离r0（也被叫作裂纹扩展半径）通常被认为是一个材料常数，它表示裂纹尖端断裂过程区的大小，可用下式进行计算[22，24，27]

为了利用考虑了裂纹尖端T应力影响的广义最大周向应变准则对试验结果进行对比分析，我们首先应得到砂岩试件裂纹尖端的临界距离r0。

为了获得砂岩裂纹尖端的临界距离r0，利用巴西劈裂法测量了经历不同干湿交替次数的砂岩试件的抗拉强度。

测量前，巴西圆盘试件的干湿交替处理过程与中心裂纹圆盘试件完全一致，每组至少包含4 个圆盘试样进行巴西劈裂试验。试验结果列于表2 中，同时根据式（10）计算的临界距离r0也一并列于表2 中。从表中可以看出，裂纹尖端的临界距离r0随着干湿交替次数的增加而呈现出减小的趋势，韩铁林等[21]也曾观测到相同的现象。与未经处理的天然岩样相比，经历了1、3、5 和7 次干湿交替作用的砂岩试件的裂纹尖端临界距离r0分别减小了4.6%，8.8%，12.2%和14.7%。

表2 裂纹尖端的临界距离Tab.2 The critical distance from the crack tip

由此可见，干湿交替作用对裂纹尖端临界距离r0也有较大的影响。

图5 给出了试验测得的I 型分量与纯I 型断裂韧度比值、II 型分量与纯I 型断裂韧度比值的关系曲线图；同时，基于广义最大周向应变准则和广义最大周向应力准则的理论预测值也一并作于图中。

由图5 可知，基于传统的最大周向应变准则和最大周向应力（MTS）准则的理论预测值总是小于试验值，这主要是因为传统的最大周向应变准则和最大周向应力准则都只考虑了裂纹尖端的奇异项，而忽略了裂纹尖端非奇异项（如T应力）的影响。

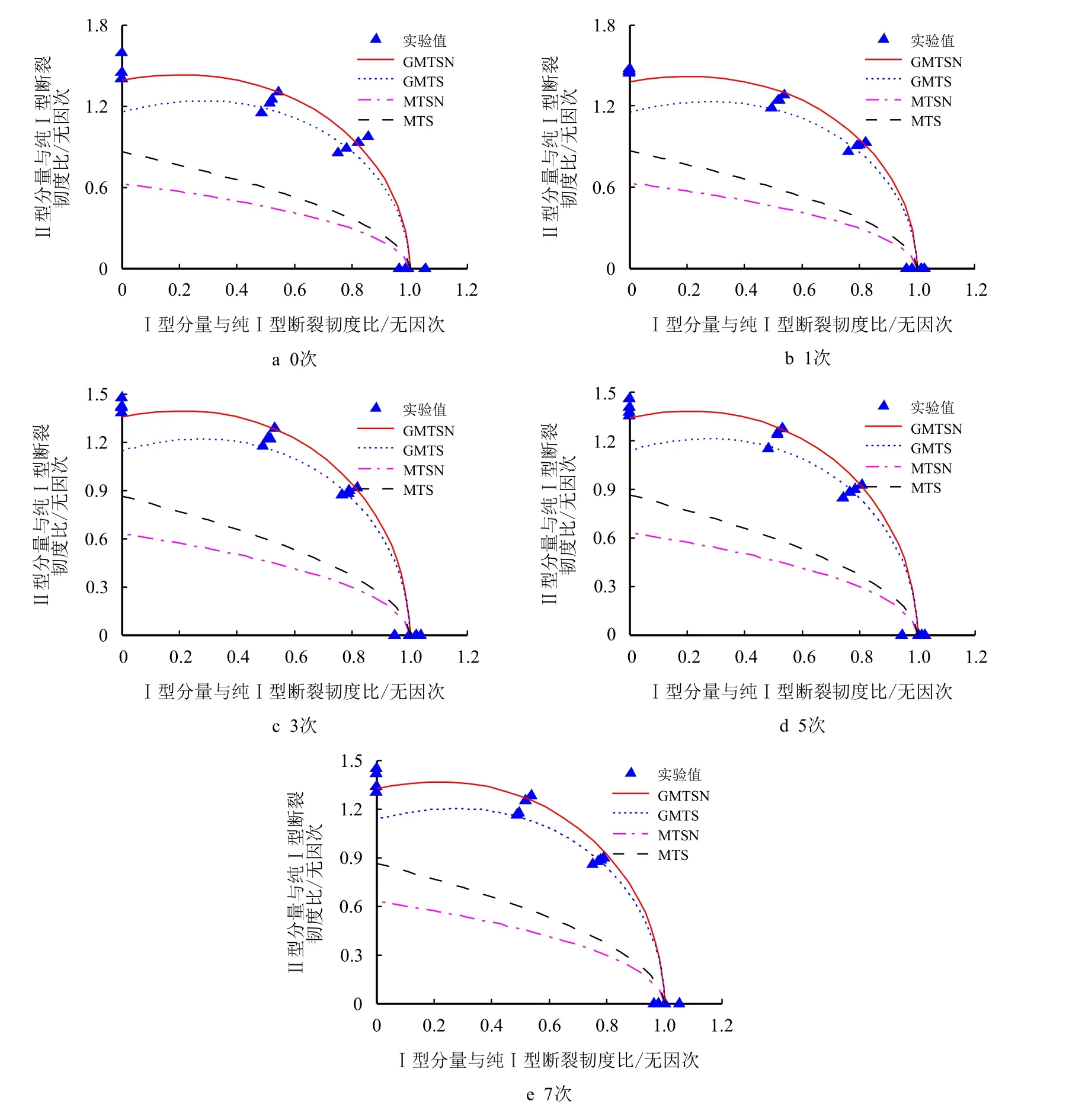
图5 砂岩复合型断裂韧度理论值和试验值的对比Fig.5 Comparison of mixed mode fracture toughness of sandstone obtained for the test results with theoretical values of fracture criteria

基于考虑了T应力影响的广义最大周向应变准则和广义最大周向应力准则的理论值与试验测试结果符合的较好。

另外，I～II 复合型加载时，I 型分量与纯I 型断裂韧度比值和II 型分量与纯I 型断裂韧度比值均随着干湿交替次数的增加而呈现出略微减小的趋势。

为了便于分析和讨论纯II 型时的情形，我们将砂岩的纯II 型断裂韧度与纯I 型断裂韧度的比值KIIf/KIC列于表3 中；同时，基于广义最大周向应变准则和广义最大周向应力准则的理论值也一并列于表3 中。

表3 砂岩的断裂韧度比值试验值与理论值的对比Tab.3 The theoretical and experimental results of ratio of fracture toughness for sandstone

从表3 中可以看出，纯II 型时，基于考虑了T应力影响的广义最大周向应变准则的理论预测值比基于广义最大周向应力准则的理论预测值更接近试验值。

例如，对于未经处理天然的试样，试验测得断裂韧度比值为1.470，根据广义最大周向应变准则，断裂韧度比值的理论预测值为1.394，理论预测值与试验测试值的相对误差仅为5.2%。然而，基于广义最大周向应力准则的断裂韧度比值理论值约为1.163，比试验值小约20.9%。进一步的研究表明，基于最大周向应变准则的理论预测值与试验值的最大相对误差均不超过5.6%。因此，与基于应力的广义最大周向应力准则相比，广义最大周向应变准则同时考虑了裂纹尖端的多个应力分量和泊松比的影响，故其理论预测值较与试验值吻合性更好。