新型负泊松比非充气轮胎设计及性能分析

赵 颖,宋 胜,李建重,杨洪涛

(西南大学 工程技术学院,重庆 400715)

轮胎是车辆不可或缺的部分,需具备耐用、舒适、低噪音、低滚阻和高安全性等性能[1]。要保证轮胎的安全性能,需提高轮胎接地性、稳定性和承载性能[2]。传统充气轮胎存在易漏气、易爆胎等缺陷,安全性低,因此采用弹性填充物或支撑体来取代胎压作用的非充气轮胎成为了轮胎发展的方向之一[3]。非充气轮胎不仅克服了爆胎的弊端,还具有低滚阻、经济性好、易加工成型等优点。目前主要通过对支撑体结构的改进,使非充气轮胎在一定舒适性条件下应力水平降低,承载性和稳定性提升[4]。而现有基于蜂窝式和辐条式支撑体的非充气轮胎难以实现上述目标,因此开发出具有新型支撑体结构的非充气轮胎十分必要。

针对支撑体结构的改进,文献[4]提出了一种具有连续支撑结构的免充气轮胎,该支撑结构可改善应力分布,提高轮胎的纵横向刚度和稳定性。文献[5]以规格为2.50-14的C形孔洞支撑体免充气轮胎为研究对象,设计优化了支撑体结构数量、孔洞圆弧半径、硬质弹性体宽度和硬质弹性体厚度,提高了轮胎的承载性能。文献[6]采用以板簧为支撑体,輮轮-橡胶为胎体的新型伪刚性免充气轮胎为研究对象,建立伪刚体-柔体耦合模型,对径向刚度进行了优化。文献[7]以鸟巢结构式免充气轮胎为研究对象,提出了轮胎下沉量的计算模型和理论计算方法。文献[8]指出蜂巢六边形支撑结构免充气轮胎具有更高的弹性和更快的散热性能,是目前应用较为广泛的非充气轮胎。

现有非充气轮胎仍然存在应力水平高、刚度特性和径向、侧向力学性能差的问题,而性能优异的负泊松比材料为非充气轮胎提供了新的研发思路。文献[9]指出负泊松比微结构材料因其“压缩-收缩”特性而具备优异的抗冲击性能和吸能特性,可有效抵抗剪切应力,大幅度吸收冲击能量。文献[10]研究了新型蜂窝结构在吸能盒中的应用,并对其结构质量、有效总吸能和峰值撞击力进行了多目标优化。文献[11]提出了一种内凹三角形负泊松比微结构材料,该材料比内凹六边形负泊松比材料吸能更平稳,压缩量也更大,并随着冲击速度的提高,表现出更强的能量吸收能力。文献[12]总结了现有常见的负泊松比内凹微结构,有内凹六边形蜂窝模型、内凹三角形模型和星形模型等。

本文在现有非充气轮胎与负泊松比微结构材料的研究基础上,综合国内外学者已有经验,提出一种新型负泊松比非充气轮胎。该非充气轮胎由胎面、支撑体结构和轮毂3部分组成,支撑体结构采用具有负泊松比特性的凹四边形微结构,该微结构具有“压缩-收缩”的加载强化特性。采用ANSYS软件对该新型结构形式的非充气轮胎进行有限元仿真分析,分别研究不同支撑体结构参数对轮胎应力、应变分布、径向和侧向刚度的影响规律,最终得出一种综合性能较好的非充气轮胎,并采用近似等体积法,将其与六边形蜂窝式非充气轮胎在应力水平和刚度性能方面进行对比分析,验证该非充气轮胎在应力水平和刚度性能方面的优越性。为进一步验证所设计的新型负泊松比非充气轮胎的性能优越性,通过3D打印制造出同比例缩小的三维样件,并与六边形蜂窝轮胎进行实验对比分析。

1 新型负泊松比非充气轮胎有限元模型

1.1 有限元模型建立

1.1.1 三维模型构建

本文不考虑轮胎和轮辋的具体接触关系,将地面和轮辋作为刚体处理,设置地面杨氏模量值为轮胎的103倍,忽略地面受压所引起的变形,忽略轮胎胎面三维模型[13,14]。所建立的三维结构模型分别如图1(a)和图1(b)所示,并建立适用于中小型车辆的规格为175/70 R15的非充气轮胎及地面的三维模型,如图2所示。在设计支撑体结构时,凹四边形负泊松比微结构中斜度较小的部分相较于同等半径下的圆弧总长度较小且形状近似可忽略,同时为避免产生不必要的孔隙结构,将其简化为圆形分隔层,考虑等效理论,其厚度设定为微结构元胞厚度的2倍。该支撑体结构具有4层厚度相同的圆形分隔层,分别隔开每层支撑条,支撑条为凹四边形负泊松比微结构,设定每层支撑条的厚度和对数均相同。

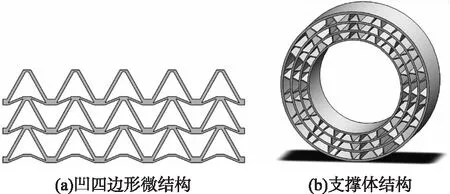
图1 凹四边形微结构和支撑体结构示意图

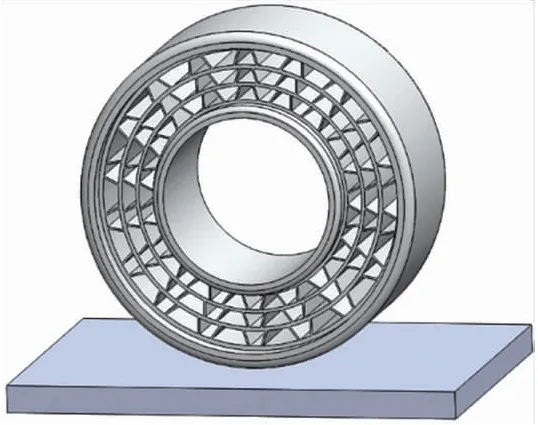
图2 轮胎结构模型示意图

支撑体结构包括单层支撑条对数、支撑条厚度、单对支撑条顶角角度等结构参数,如图3所示。选择如表1所示的不同结构参数的支撑体,分析不同参数对轮胎应力、应变水平和刚度特性的影响。

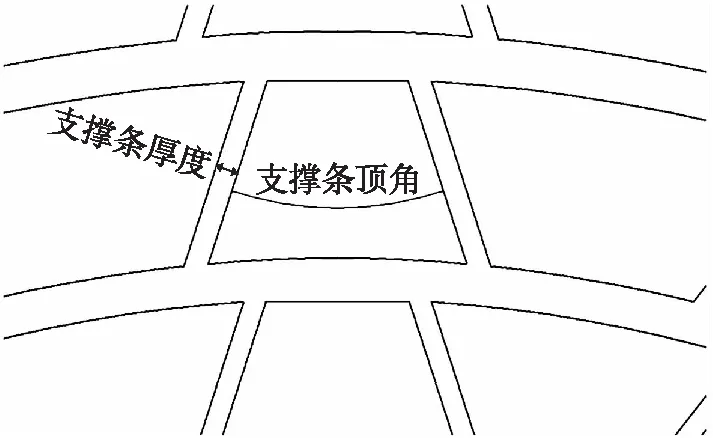
图3 单对支撑条结构主要参数示意图

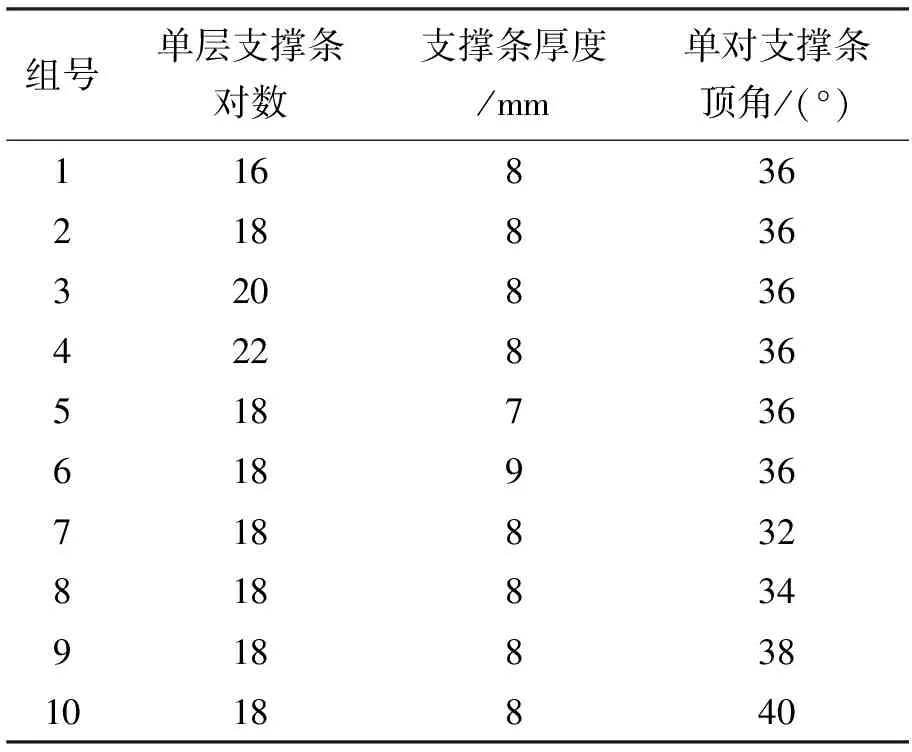
表1 支撑体结构参数表

1.1.2 材料和单元模型

轮胎有限元模型由轮辋、支撑体微结构、胎面、路面4部分组成,如图4所示。轮辋和路面做刚化处理,而支撑体微结构选择具有超弹性的聚氨酯材料,其本构模型采用橡胶超弹性材料模型Moony-Rivlin模型,胎面选择线弹性聚氨酯材料。支撑体结构材料密度为1 240 kg/m3,材料常数C10为2.99×105Pa,材料常数C01为2.49×106Pa,不可压缩参数D1为0.01 Pa-1,胎面材料密度为103kg/m3,杨氏模量为1.3×108Pa,泊松比为0.4。采用SOLID186单元,默认生成六面体单元,单元大小为30 mm。

图4 轮胎有限元模型示意图

1.2 载荷和约束条件

分析轮胎承载和接地性能时均需固定地面,轮辋处施加位移30 mm,施加载荷方向竖直向下。进行径向刚度分析时,约束条件与上述相同,只需施加不同位移使载荷条件等同于实际工作情况下轮辋处的受力6 kN。计算侧向刚度时固定轮辋,对地面施加一定竖直向上的位移,模拟施加位移值后等效于静态载荷下轮胎的实际工作情况。最后对轮胎整体施加横向位移30 mm,模拟轮胎相对于地面的侧向移动。本文在轮胎与地面接触分析中,均采用有摩擦的接触对frictional,设定两者之间的摩擦因数为0.4。frictional为ANSYS内设置的一种有摩擦的接触方式,2个接触面可以法向分离和切向滑动。

1.3 收敛性验证

为解决施加载荷过大或支撑体单层支撑条密度过大导致轮胎被压溃或结构之间互相干扰而不能收敛的问题[15],首先对轮辋处施加位移,采用ANSYS软件后处理模块中的探针工具探测轮辋处受力。为获得接近实际工作载荷的施加力,至少需要2次仿真分析,第1次在较大位移下查看轮辋处受力,第2次基于前次结果通过插值法适当调整,以初步得到所需施加力值对应的位移值,多次模拟后得到接近实际工作载荷大小的施加力。其次,为保证轮胎不被压溃,仿真分析时轮胎单一方向上所施加的最大位移不超过30 mm,且支撑体单层的支撑条不能过多。最后,为获取较好的计算收敛性,采用手动设置分步数,子步定义为103步,通过迭代求解器求解,采用Augmented Lagrange算法计算胎体与地面的接触对。为避免网格不收敛导致计算结果不准确,在模型参数完全一致的前提下建立多组网格单元大小不同的有限元模型进行分析,同时考虑计算准确性与耗时,认定结果波动比小于5%时网格收敛[16],最终确定六面体单元大小为30 mm时设计合理。

1.4 有限元模型验证

为验证本文所建立的有限元模型的可靠性和准确性,采用3D打印技术制造出规格为175/70 R15轮胎的等比例缩小模型,以模拟实际工况。基体材料选用丙烯腈/丁二烯/苯乙烯共聚物(ABS),其密度ρ=1.05g/cm3,泊松比μ=0.33,弹性模量E=2×103MPa。实验台加载速度设置为v=2 mm/min,样件高度、宽度都为147 mm,图5为新型负泊松比非充气轮胎压缩实验实物图。由于轮胎承受载荷发生形变时,其接触面积变化,其真实的应力值无法测得,因此本文对轮胎样件做静载荷加载实验得到其沉降-载荷曲线,同时对比相同约束条件和载荷工况下的有限元模型仿真数据如图6所示。

图5 新型负泊松比非充气轮胎压缩实验实物图

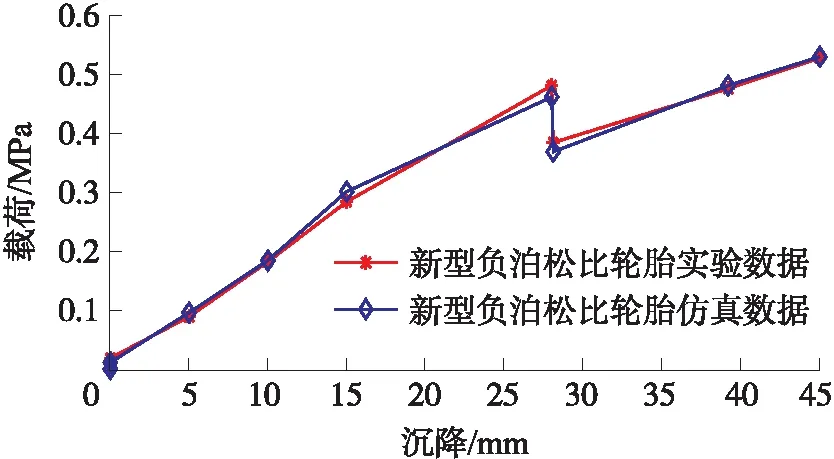
图6 新型负泊松比轮胎沉降-载荷实验与仿真数据对比图

由图6可以看出,实验与仿真曲线趋势一致,结果相近且误差在4.07%之内,验证了本文所建立有限元模型的可靠性与准确性。

图7 不同单层支撑条对数的轮胎和胎面最大应力对比图

2 支撑体结构对轮胎性能的影响

2.1 单层支撑条对数对轮胎应力、应变的影响

设定支撑条厚度、单对支撑条顶角角度不变,改变支撑条对数,在6 000 N同等载荷下,分析不同单层支撑条对数对轮胎和胎面应力、应变的影响,分别如图7和表2所示。

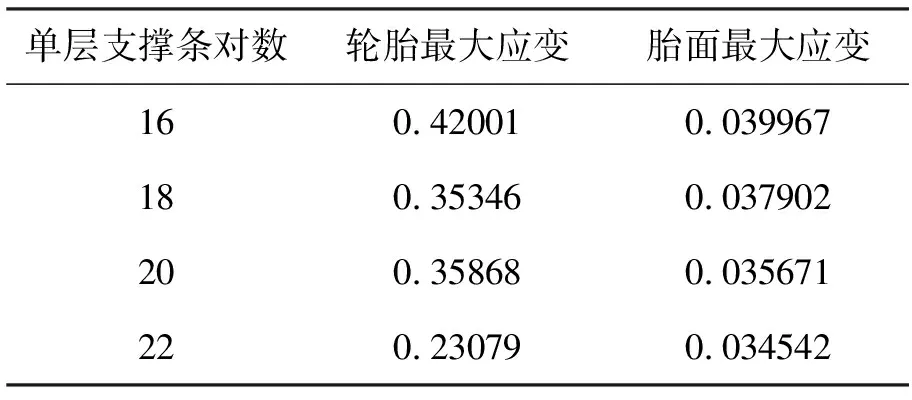
表2 不同单层支撑条对数的轮胎和胎面最大应变表

随着单层支撑条对数的增大,轮胎和胎面的最大应力与最大应变整体呈下降趋势。当单层支撑条对数为18和20时,轮胎所受的最大应力变化不大。当选取单层支撑条对数为18时,轮胎使用寿命较长且可满足轻质需求,此时轮胎与胎面的应力、应变分布分别如图8和图9所示。

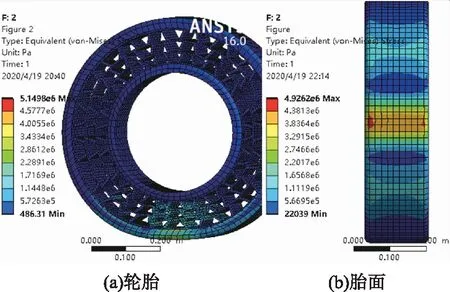
图8 单层支撑条对数18对的轮胎及胎面应力分布图

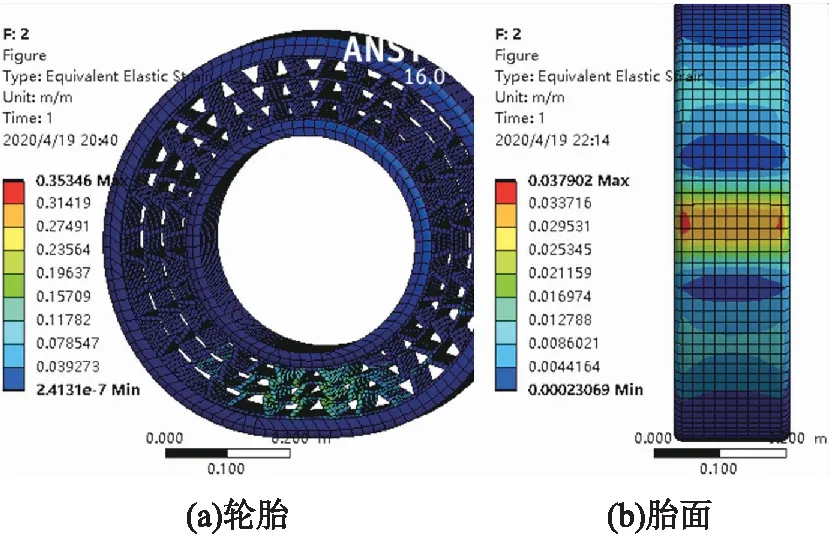
图9 单层支撑条对数18对的轮胎及胎面应变分布图

由图8和图9可知轮胎最大应力和最大应变分布于支撑结构转折处,而胎面与地面接触部分的最大应变值较小。表2也表明,随着单层支撑条对数增加,胎面接地处最大应力减小较快,胎面最大应变也呈下降趋势。综上所述,轮胎支撑条结构转折处容易产生疲劳损坏,接地处两侧均有小部分区域容易磨损。

2.2 支撑条厚度对轮胎应力、应变的影响

由表1中的第2、5、6组数据,支撑条厚度分别取7 mm、8 mm和9 mm,在6 000 N同等载荷条件下,分析不同支撑条厚度对轮胎和胎面应力、应变的影响,结果分别如图10和表3所示。

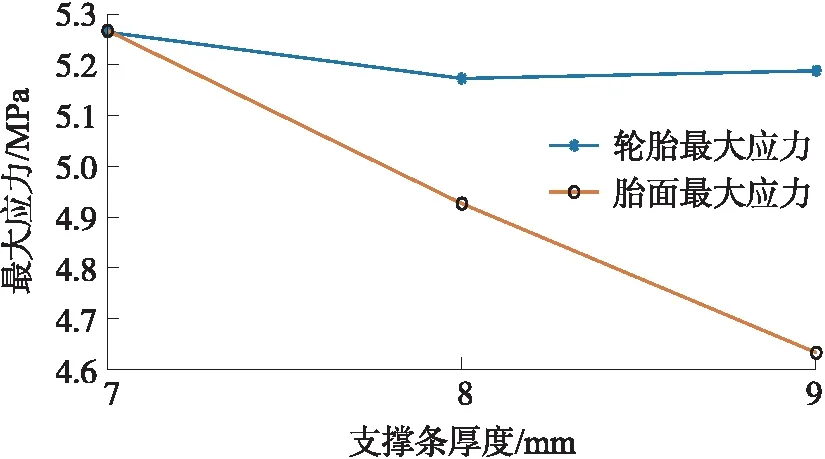
图10 不同支撑条厚度的轮胎和胎面最大应力对比图

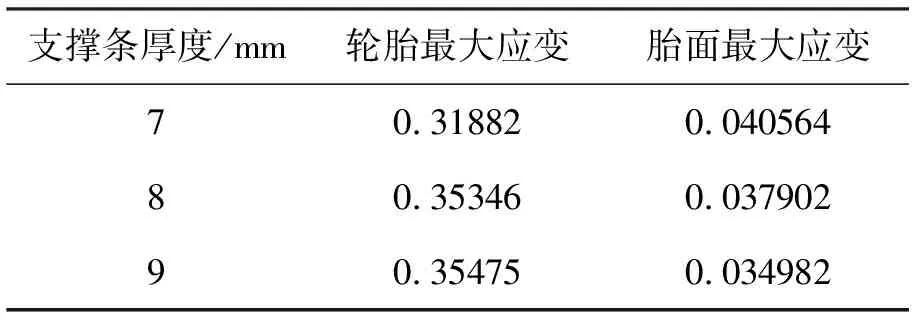
表3 不同支撑条厚度的轮胎和胎面最大应变表

支撑条厚度从7 mm增加到9 mm,轮胎最大应力先下降再小幅上升,变化趋势平稳,表明支撑条厚度对轮胎工作应力影响不大。支撑条厚度为8 mm时轮胎和胎面应力、应变分布如图11、图12所示。

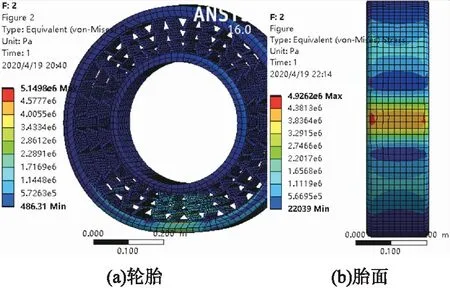
图11 支撑条厚度8 mm的轮胎及胎面应力分布图

图12 支撑条厚度8 mm的轮胎及胎面应变分布图

如图11所示,最大应力出现在支撑条结构的转折处和胎面接地处。由表3和图12可以得出,轮胎最大应变随支撑条厚度的增加呈增大趋势,最大应变同样出现在支撑条结构转折处。综合对比可知,当支撑条厚度为8 mm时,轮胎的最大应力最小且比使用支撑条厚度为9 mm的轮胎更节省材料。

2.3 不同单对支撑条顶角对轮胎应力、应变的影响

取表1中第2、7、8、9、10组结构数据,建立5个仅支撑条顶角θ大小不同的三维模型,其中,第2组为36°,第7～10组分别为32°、34°、38°、40°,在6 000 N同等载荷下,分析不同支撑条顶角对轮胎和胎面应力、应变的影响,如图13和表4所示。

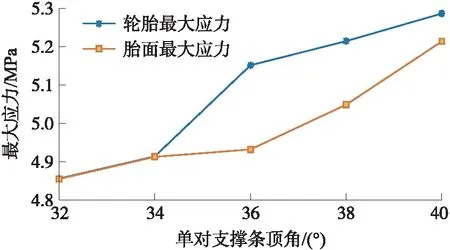
图13 不同单对支撑条顶角的轮胎和胎面应力分布图

表4 不同单对支撑条顶角的轮胎和胎面最大应变表

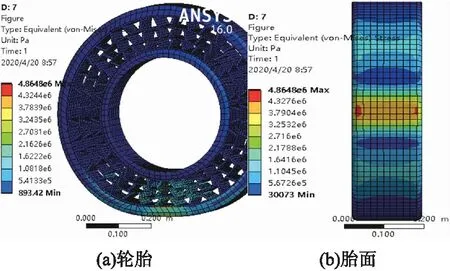
图14 单对支撑条顶角32°的轮胎及胎面应力分布图

从图13可知,随着支撑条顶角的增大,其最大应力值呈上升趋势,轮胎和胎面整体的最大应变也呈上升趋势,其中支撑条顶角为32°时轮胎的最大应变值最小,胎面接地处的最大应变值最小。因此,当支撑条顶角大小为32°时,轮胎的最大应力较小,能有效减少轮胎疲劳损坏的发生。以单对支撑条顶角为32°为例,其轮胎及胎面的应力、应变分布分别如图14和图15所示。

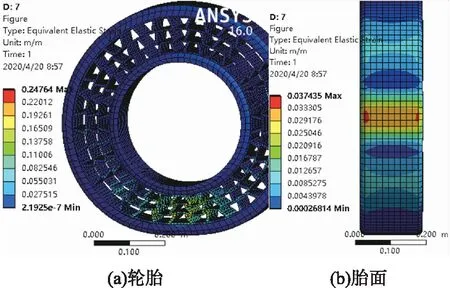
图15 单对支撑条顶角32°的轮胎及胎面应变分布图

轮胎最大应力主要分布在胎面接地处和支撑条结构的转折处,最大应变位于支撑条结构的转折处,且轮胎接地部分的最大应力随支撑条顶角角度增大而增大。在静载工况下,通过对10组不同支撑条对数、支撑条厚度、单对支撑条顶角大小的非充气轮胎进行应力、应变分析可得:当支撑条对数为18左右、厚度为8 mm、顶角为32°左右时,可获得应力最大、应变较小、疲劳磨损相对较小的非充气轮胎。

3 新型非充气轮胎刚度特性

以支撑条对数n分别为16、18、20、22,顶角角度θ分别为32°、34°、36°、38°、40°,厚度d分别为7 mm、8 mm、9 mm,建立轮胎三维模型,在6 000 N工作载荷条件下计算径向刚度。不同支撑条对数对轮胎径向力和径向位移的影响如图16所示,对轮胎侧向力和侧向变形的影响如图17所示。根据有限元分析结果,不同支撑条对数的轮胎刚度特性值如表5所示。不同支撑条顶角对轮胎的径向力和径向位移的影响如图18所示,对轮胎侧向力和侧向变形的影响如图19所示。

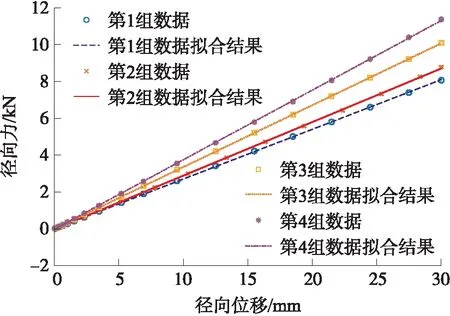
图16 不同单层支撑条对数的轮胎径向力与径向位移关系曲线图

图17 不同单层支撑条对数的轮胎侧向力与侧向变形量关系曲线图

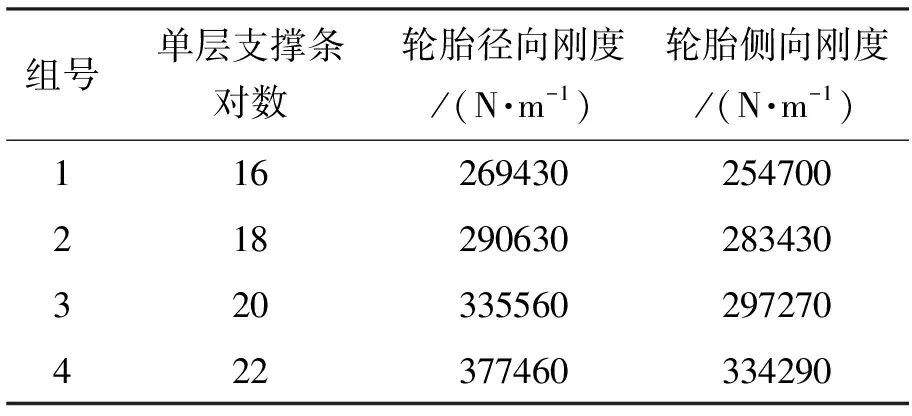
表5 不同单层支撑条对数的轮胎刚度特性值表

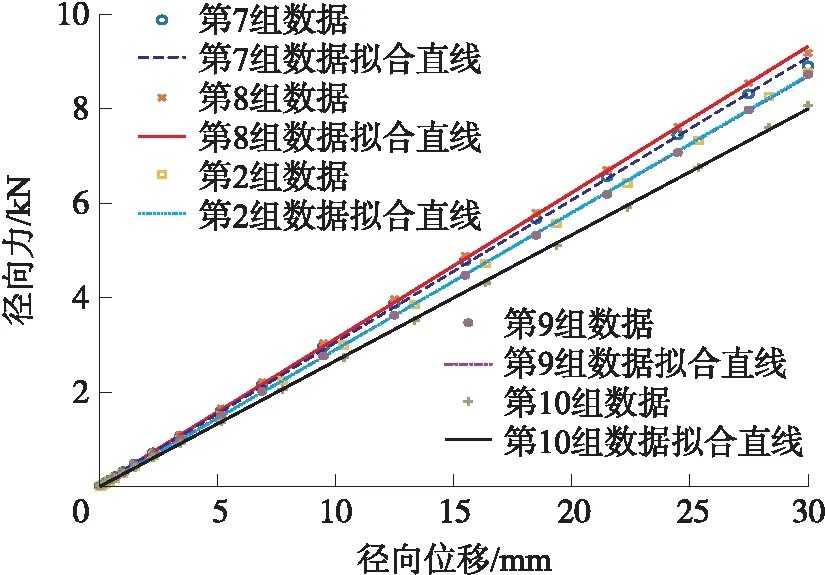
图18 不同单对支撑条顶角的轮胎径向力与径向位移关系曲线图

图19 不同单对支撑条顶角的轮胎侧向力与侧向变形量关系曲线图

根据有限元分析结果,不同支撑条顶角的轮胎刚度特性值如表6所示。不同支撑条厚度对轮胎的径向力和径向位移的影响如图20所示,对轮胎侧向力和侧向变形的影响如图21所示。根据有限元分析结果,不同支撑条厚度的轮胎刚度特性值如表7所示。

表6 不同单对支撑条顶角的轮胎刚度特性值表

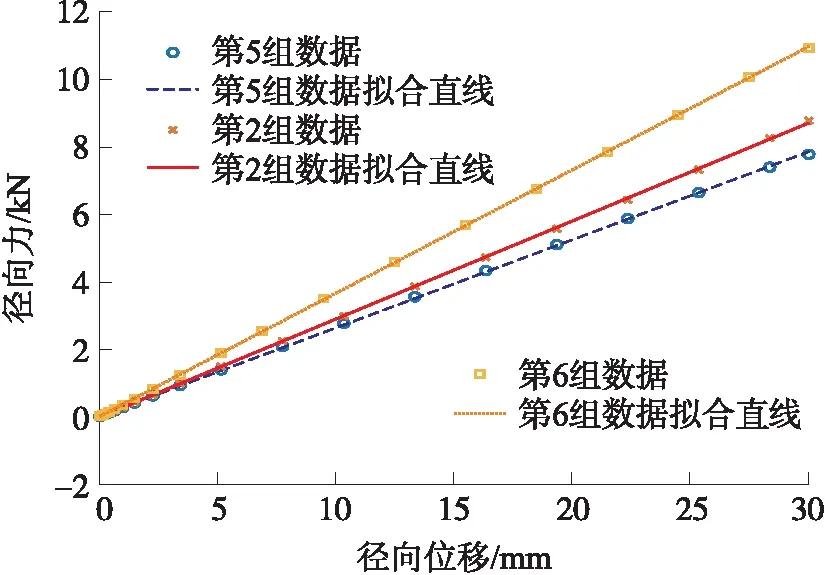
图20 不同支撑条厚度的轮胎径向力和径向位移关系图

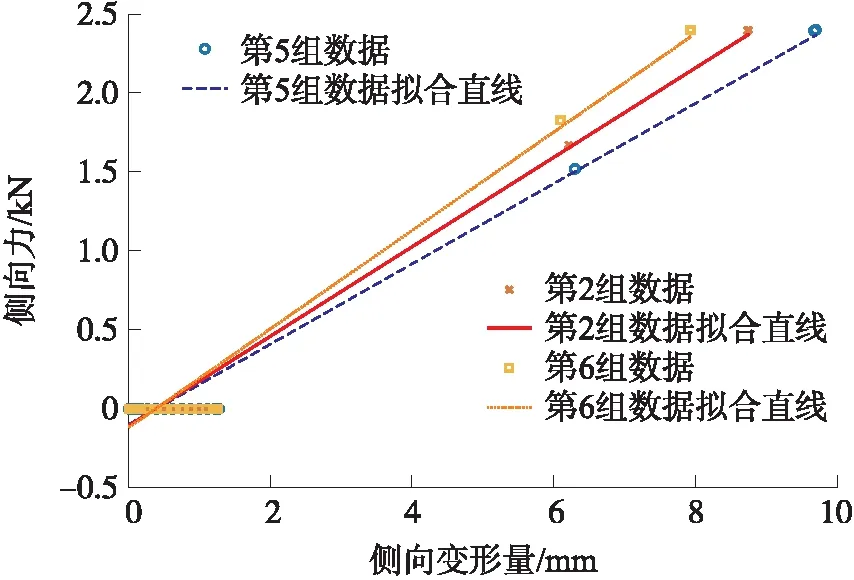
图21 不同支撑条厚度的轮胎侧向力和侧向变形量关系图

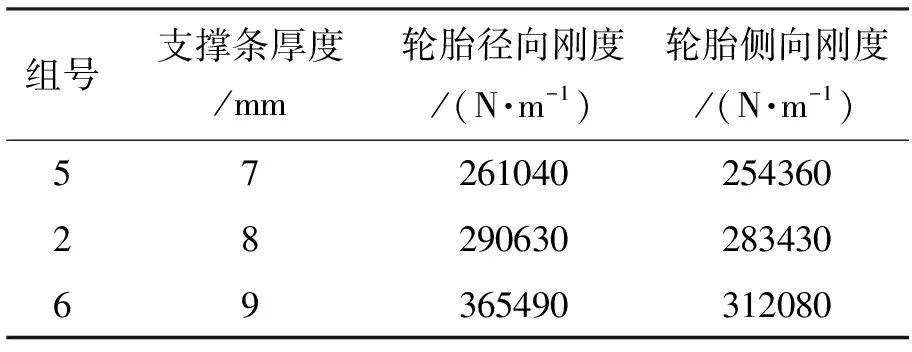
表7 不同支撑条厚度的轮胎刚度特性值表

结合图16、图18及表5可看出,新型非充气轮胎的径向刚度与侧向刚度随单层支撑条对数增大呈现增长趋势,表明支撑条对数越多,新型非充气轮胎的径向刚度、侧向刚度越大,承载性能、径向稳定性及侧向稳定性更好。

由表6可知,新型结构非充气轮胎的径向刚度与侧向刚度随支撑条顶角增大基本呈现减小的趋势。结合图18、图19可得出:在顶角范围为32°～34°时,轮胎的径向刚度变化不大;相似地,在顶角角度较小,为32°～36°时,支撑条顶角大小对轮胎侧向刚度影响也较小;而顶角角度较大,为38°～40°时,支撑条顶角大小对轮胎侧向刚度的影响较为明显。由此说明,支撑条角度在32°～40°范围内,若要提高轮胎的径向刚度与侧向稳定性,应选择支撑条顶角较小的轮胎。

结合图20、图21及表7可看出,新型非充气轮胎的径向刚度与侧向刚度随支撑条厚度增大而增大。当支撑条厚度由7 mm增加到9 mm时,其径向刚度大幅度提高,这表明在满足经济性条件时,适当提高轮胎支撑条厚度,可以极大地提高轮胎的径向刚度和侧向刚度,继而提高轮胎的承载能力。

4 新型非充气轮胎与六边形蜂窝轮胎对比分析

由2.2节可知,支撑条厚度为8 mm时,轮胎的最大应力和应变均比支撑条厚度为9 mm的轮胎小。为在保证较优的径向刚度和侧向刚度的同时,突出新型轮胎轻量化需求,选择支撑条厚度为8 mm。而支撑条对数为18对时的最大应力和应变都较22对时小,选用支撑条对数为18对,顶角角度32°时各项数据都是最优。故综合各项因素,并着重关注新型轮胎的轻量化设计,选用支撑条对数为18、顶角角度为 32°、厚度为8 mm的新型凹四边形微结构负泊松比非充气轮胎。

基于前文对新型非充气轮胎的性能分析,选择综合性能相对较优的第7组非充气轮胎,并令其与同规格的六边形蜂窝式非充气轮胎进行对比。由于轮胎的胎面和轮辋部分固定不变,只需要使同规格的六边形蜂窝式非充气轮胎的支撑体结构体积与新型负泊松比非充气轮胎接近,即可实现该2种轮胎所需材料的质量大致相同。因此,新型非充气轮胎支撑体体积为56 662×150 mm3,六边形蜂窝式非充气轮胎支撑体体积为56 648×150 mm3。

4.1 轮胎应力分析

基于以上有限元分析过程,得到2种轮胎应力分布如图22所示,新型非充气轮胎最大应力为4.609 1,六边形蜂窝式非充气轮胎最大应力为4.842 2。如图22所示,2种轮胎胎面的应力分布情况大致相同,两者最大应力值均位于轮胎的胎面内部,有较小区域位于胎面接地处。可知,在同等工作载荷下,新型结构非充气轮胎最大应力值小于六边形蜂窝式非充气轮胎,最大应力减小4.81%,说明这2种轮胎的胎面内部容易疲劳损坏,但新型非充气轮胎相较蜂窝式轮胎有效降低了胎面损坏的可能性。

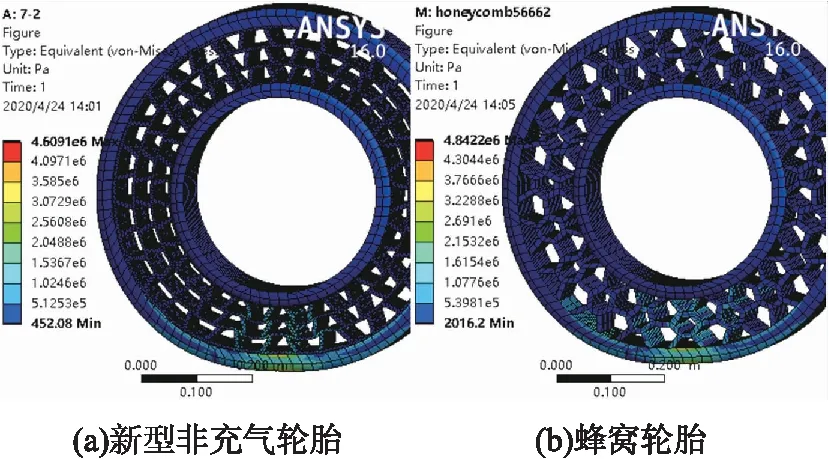
图22 轮胎应力分布图

4.2 轮胎双向刚度对比

新型非充气轮胎和蜂窝式轮胎的径向力和径向位移对比如图23所示,侧向力和侧向变形的对比如图24所示。通过有限元计算分析得到2种轮胎的双向刚度值如表8所示。

图23 2种轮胎径向力和径向位移关系图

图24 2种轮胎侧向力和侧向变形量关系图

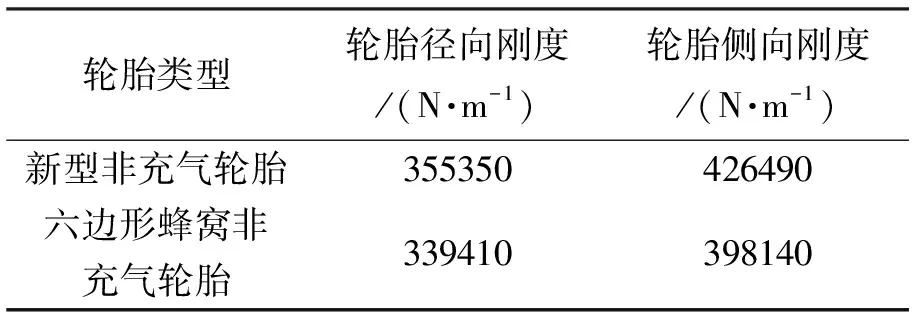
表8 2种轮胎刚度特性值表

对比可知,新型非充气轮胎的径向刚度比六边形蜂窝式轮胎的径向刚度增大4.7%,侧向刚度增大7.12%。新型非充气轮胎的径向刚度进一步增强了其承载能力,能在一定程度上提高车辆舒适性,同时轮胎侧向刚度提升,使得新型非充气轮胎的侧向稳定性优于六边形蜂窝式非充气轮胎。

5 新型负泊松比非充气轮胎与六边形蜂窝式非充气轮胎实验对比

考虑到基体材料的可制造性和易获得性,并忽略基体材料种类不同对轮胎性能的影响,着重探究凹四边形负泊松比微结构对轮胎的应力水平和刚度特性的影响,验证凹四边形负泊松比微结构较传统蜂窝式结构的优越性能。以上文中提到的由ABS材料制造而成的新型凹四边形负泊松比非充气轮胎结构与六边形蜂窝轮胎结构为研究对象,可同时获得2种轮胎沉降-载荷曲线对比图,如图25所示。由图25可知,在相同沉降下,负泊松比非充气轮胎承受载荷时对塑性变形的抵抗力较大,即保持弹性形变的区域较大,更稳定,承载性能较好。此外,图25中沉降-载荷曲线的骤然下降的部分是屈服阶段。新型负泊松比非充气轮胎比蜂窝轮胎发生屈服的临界载荷值高,即强度高,稳定性能优异。

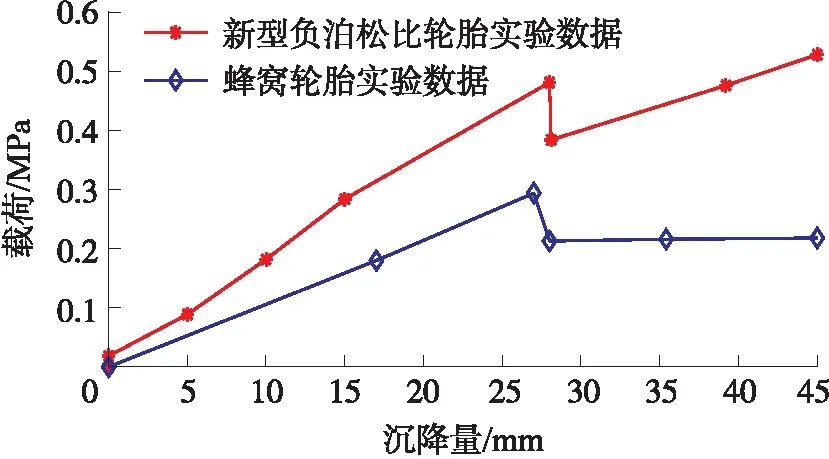
图25 2种轮胎沉降-载荷曲线对比图

6 结束语

本文提出了一种负泊松比非充气轮胎支撑体凹四边形微结构,建立了凹四边形负泊松比非充气轮胎有限元模型,采用3D打印技术制造样件进行沉降-载荷实验,验证了所建有限元模型的准确性。通过ANSYS软件对不同支撑体结构参数的负泊松比非充气轮胎进行了有限元仿真,优化分析了轮胎的应力水平和刚度特性,选出了性能最优的新型负泊松比非充气轮胎,并与同规格下的六边形蜂窝式非充气轮胎在应力水平和刚度性能方面进行了仿真对比分析。最后,为进一步验证优化设计的新型负泊松比非充气轮胎在承载方面的性能优越性,通过3D打印制造出同比例缩小的实验样件,与六边形蜂窝轮胎进行对比,得出如下结论:

(1)负泊松比支撑体结构的非充气轮胎表现出良好的应力水平,径向刚度和侧向刚度性能均比较好。

(2)增大支撑条厚度,能较大地提升轮胎的应力水平和径向、侧向刚度;减小单对支撑条的顶角角度,一定程度上可以减小轮胎的最大应力,较大提升轮胎的径向刚度;当单层支撑条对数在18对左右时,轮胎既能节省材料又可以保持较优的应力水平和刚度性能。

(3)新型负泊松比非充气轮胎比六边形蜂窝式非充气轮胎的最大应力明显减小,虽然六边形蜂窝式非充气轮胎的径向刚度略大于新型负泊松比非充气轮胎,但是后者拥有更好的侧向刚度特性和稳定性。

(4)与传统六边形蜂窝非充气轮胎相比,相同应变下,负泊松比非充气轮胎承受载荷时对塑性变形的抵抗力较大,即保持弹性形变的应力区域较大,更稳定,承载性能较好。