基于改进文化基因算法的轧制规程优化

王海霞,张 兵,芮延年,尤凤翔

(1.苏州大学 应用技术学院,江苏 苏州 215325;2.华东交通大学 交通运输与物流学院,江西 南昌 330013;3.江苏大学 机械工程学院,江苏 镇江 212011)

随着国内有色金属板带材加工技术的飞速发展,大型铝板带热连轧生产线的建设逐年增多。从第1条铝(1+4)热连轧国产生产线在河南明泰铝业公司正式投产,到西南铝业有限公司引进国际先进连轧产线,国内有色金属热连轧建设急剧升温,形成年产500万t以上产能,至此我国铝板带材的产品数量和质量被推上了新高度。但引进成熟产线并不等于能够产出满足市场需求的合格产品。在热连轧生产过程中,影响铝板带产品的因素很多,其中产线轧制规程即负荷分配技术的优劣最为重要,它直接影响产品质量、工厂能耗和生产过程的稳定性。因此负荷分配是有色金属板带材加工技术的关键环节,也是板带材轧制加工工艺领域非常重要的研究目标。

1 轧制规程分配方法

铝热连轧轧制规程是连轧工艺的核心问题,在一定轧制条件下,通过提高轧制力并计算模型精度来优化负荷分配。建立精确的铝带材变形率、速度变化、终轧温度及不同合金牌号的变形抗力预报模型,同时确定连轧机各机架的道次压下率,这样各机架入口、出口厚度及轧制压力等参数也随之确定[1]。

最早的负荷分配方法有经验法和能耗曲线法[2]。经验法把操作手经验参数录入数据库以供调用,方法简便易行。李维刚等[3]提出了一种铝轧制过程中基于经验的负荷分配方法,但方法中没有进行机组负荷的均衡分配。李海军等[4]介绍了能耗曲线法在轧制规程中的应用,采集轧制数据后计算各机架出口厚度h和生产能耗ec的比例,画出h-ec曲线,进行轧制规程的指导,可以降低机架间负荷不均概率。但现场大量数据的采集比较困难,不适合众多规格牌号和大批量铝板带轧制生产。

近几年,制定规程时引入了最优技术,用目标函数的形式来表示最终要求。在约束条件下,寻找最佳出口厚度等多种参数的分配方案,并要求其目标函数值最小,以此得到满足工艺要求的最优负荷分配。其中最关键的问题是确定优化方法和建立目标函数。谭成楠等[5]用一种补偿误差的迭代方法,改进了神经网络,对负荷分配的仿真效果非常好。王仁忠等[6]采用动态自适应规划法进行寻优计算,可以得到理论唯一解,但最优唯一解获取困难,尤其当使用单目标函数时,因为个别接近极限的约束条件,难以达到负荷目标的均衡。

综上,针对热连轧机组的特征和现有优化算法,在实际生产应用中存在着迭代过程计算量大、收敛速度慢等问题。本文提出了一种基于文化基因算法(Memetic algorithm,MA)的轧制规程优化算法,外部框架采用基于种群的改进自适应遗传算法(Adaptive genetic algorithm,AGA)做全局搜索和一次局部搜索,通过改进遗传操作提高种群的多样性。采用简化序列二次规划(Reduced successive quadratic programming,RSQP)来进行二次局部搜索。通过仿真和实际生产对算法进行了可行性验证,结果表明:MA优化后的方案可实现负荷的均衡分配,板带材终轧板形质量较现有算法提升了10.8%。

2 铝热连轧数学模型

2.1 轧制力模型

在轧制过程中,轧制力数学模型是其他参数模型的基础,目前用于铝板带热连轧的计算公式是西姆斯公式

(1)

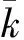
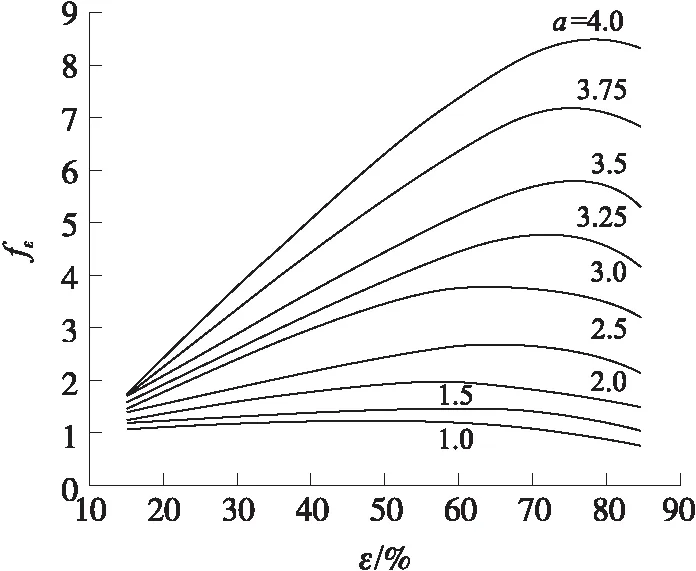
图1 fε(a,ε)图

式(1)中各变量表达式:

(1)变形抗力公式

(2)

(3)

式中:β为张力影响系数,通常取0.7,σenter、σexit分别为入口、出口侧张应力,出口侧张应力的作用大于入口侧张应力。

(2)接触弧长ld公式

(4)

(5)

Δhi=hi-1-hi

(6)

式中:R′为压扁变形后的轧辊半径,R为工作辊半径,hi为绝对压下厚度,hi-1为第i个机架厚度H。在接触弧长ld计算过程中考虑了工作辊的压扁半径R′,式(5)中轧制力P可用迭代法求出。

(3)系数Qp用希尔(Hill)公式计算,如式(7)、(8)所示

(7)

(8)

式中:μ为接触弧长ld的摩擦系数,ε为压下率,α为辊间油膜影响系数,ν为带材出口速度。

2.2 厚度分配模型

厚度分配是铝热连轧轧制规程的基础功能。连轧机组在各机架轧制力作用下,将初始厚度为H的铝板带材轧制成最终厚度为hn的成品,总压下量为:Δh=H-hn。轧机结构模型如图2所示。

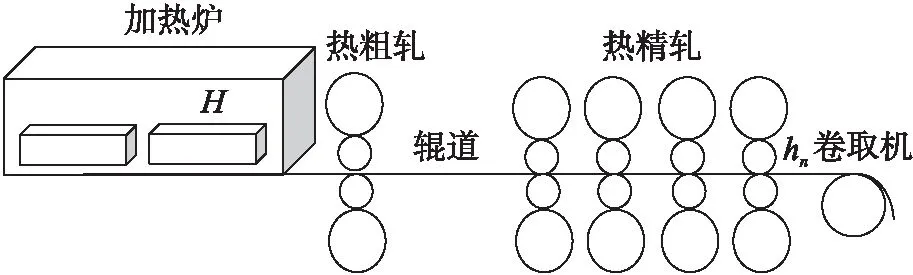
图2 铝热连轧(1+4)轧机模型图

铝热连轧生产中根据单位能耗和终轧厚度hn进行计算,最终将能耗曲线转换成各机架出口的厚度基准值,如式(9)、(10)所示

(9)

(10)

式中:σ1、σ2为累计能耗系数,Pn为n个机架的总轧制力,φi为第n个机架的负荷分配比,hi为第i个机架的出口带材厚度,i=1,2,…,5。

3 目标函数与约束条件

本文以等相对功率裕度、良好板形及可变目标作为轧制规程优化的目标函数。

(1)等相对功率裕度目标函数。

本文在某厂铝热连轧(1+4)轧机上进行实验,该轧机机架间额定轧制功率不相等。为平衡各机架主电机的负荷,使各机架设备充分发挥最大作用。目标函数设定为

(11)

式中:Ni为第i机架主电机消耗的总功率,Nhi为第i机架主电机的额定功率,n=5。

(2)良好板凸度目标函数。

规程中目标板凸度策略是在前4机架板凸度均衡分配的基础上,给5机架分配合理轧制力,目标函数如下

(12)

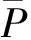
(13)

式中:MP为轧机负荷和板凸度之比,MF为弯辊力对板凸度之比,hn为轧件终轧出口厚度,C0为轧件原始凸度,h0为轧件原始厚度,εΣ为综合工作辊辊型参数,ρΣ为综合工作辊辊型影响因子,F为弯辊力。

(3)可变目标函数。

热连轧轧制过程可变目标函数分为2个阶段。第1阶段为2、3、4机架用最大压下量轧制提高产量。目标函数为

J3=min((P1-K1P2)2)

(14)

第2阶段为用等压力分配来提高设备利用率,目标函数为

J4=min((P2-K2P3)2)

(15)

式中:K1、K2分别为2阶段机架轧制力之比。

最优综合目标函数为

(P1-K1P2)2+(P2-K2P3)2}

(16)

在制订轧制规程时,必须满足2个约束条件。

(1)设备能力约束:各机架上的轧制力应小于最大允许值

Pi≤PimaxMi≤KMNTimin≤Ti≤Timax

式中:Pi为各机架的轧制力,Mi为各机架电机转矩,MN为各机架电机额定转矩,K为电机过载系数,Ti为各机架张力。

(2)板凸度约束:合理安排前后机架的压下率,使轧制力按照一定的比例,即εimin≤εi≤εimax。式中:εi为各机架压下率。

4 改进的文化基因算法

本文改进的文化基因算法外部框架选择AGA,二次局部搜索采用RSQP法来进行规程的优化。遗传算法自适应搜索方式性能优越,对起始点要求宽松,搜索过程灵活,用随机方式能找到问题的全局最优解。但GA操作产生的个体随机性太大,不能确定最优方向,且在最优解附近局部搜索能力减弱[8,9]。本文在保持GA优点的基础上,使用自适应动态技术和改进操作算子的AGA方法,来改善GA局部寻优能力差且容易早熟的问题。

SQP是最有效的非线性约束问题优化求解方法之一,它用一种近似规划法将复杂的非线性问题转化为二次规划问题求解,简化了约束条件,收敛效率高并能快速找到迭代方向,通过迭代收敛到最优解。但SQP在每一步迭代中,都需要构造多个二次函数去无限逼近目标函数,这样无法利用原问题的稀疏性和对称性求解二次函数,尤其当问题规模扩大时,计算和存储工作量变大,稳定性变差。本文对SQP进行了简化,采用简化的RSQP算法来进行局部搜索,以AGA的中间最优解为起始点,用一阶校正步来降低不可行的程度,只需求解1个二次函数即可,该二次函数的可行解必须是收敛的。本文算法可以提高全局收敛性和问题规模,减小计算量和存储量。

算法实现步骤如下:

(1)算法初始化,确定外部框架算法AGA的初始参数和二次局部搜索算法RSQP的近似矩阵。

(2)种群初始化,选取父种群,根据轧制规程特点,采用实数编码,设计专用的非标准遗传算子,使用选择、交叉、变异等运算,进行初始种群的局部搜索。

其中,选择算子用比例选择法:设N为种群大小,个体i的适应度为Fi,则i被选中概率

(17)

交叉算子采用非一致交叉运算

(18)

式中:α变量由进化代数决定,是[0,1]之间的随机数。变异算子用实质种群变异,变异步长为

(19)

式中:X和X′为变异前后的个体,ρ为个体中最大和最小值的差。

(3)进化操作,确定目标适应度函数,采用轮盘赌算子进行选择、交叉和变异运算,进行种群内局部搜索,选取最优个体形成新种群。

(4)采用自适应动态技术,提高算法参数交叉概率Pc和变异概率Pm到Pc2和Pm2,确保遗传初始种群的主要特征,同时解决全局算法的早熟问题,使全局算法的结果处于最优区域。

(20)

(21)

式中:fmax为群体中的最大适应度值,farg为每代群体中的平均适应度值,f′为2个要交叉的个体较大的适应度值,f为要变异的个体适应度值。

(5)使用概率法判断进入RSQP局部搜索的时间,判断条件

(22)

式中:fi-1(X)为上一代种群中最优目标函数值,fi(X)为当前种群中最优目标函数值,ε=10-2～10-3。

(6)以此时的全局最优解为初始解,用校正算法来修正搜索方向,同时调用RSQP近似矩阵模块进行二次局部解的搜索。

非线性约束最优化问题条件为

minf(X)

s.t.gu(X)≤0

式中:u=1,2,…,p;hν(X)=0;ν=1,2,…,m。

把f(X)在迭代点Xk简化成二次函数,约束函数s.t.gu(X)≤0转化成线性后,得到二次规划问题

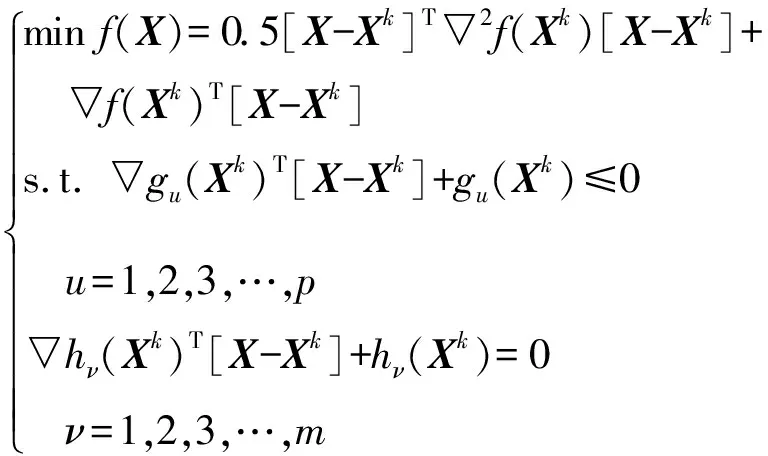
(23)

当不能达到原问题的可行点时,令dx=X-Xk,将二次规划问题变成确定搜索方向dx的问题。

(24)

通过式(24)确定dx,沿dx方向寻优得到新的可行点Xk+1。对特定的效益函数会因超线性收敛步的不可行而破坏算法的收敛性。本文对dx进行校正,使其成为一阶方向,这样只须解1个总的二次规划解即可[10]。

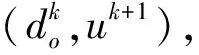
假设

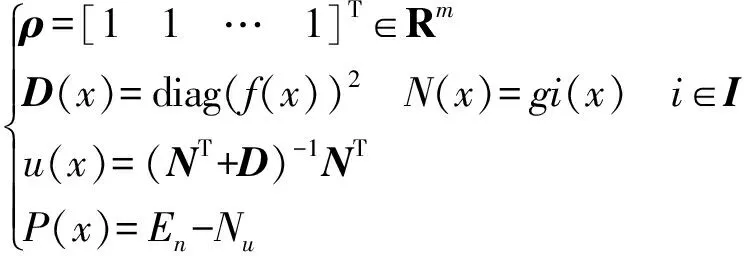
(25)

那么

(26)

(27)

当a>0时

(28)

(29)

(30)

(31)

通过以上计算,得到逼近原约束问题的最优解。

(7)将二次局部搜索的最优解代入AGA中再次进行全局寻优,判断迭代次数,次数未到则跳转到步骤(2),否则结束算法输出最优解。

算法流程图如图3所示。

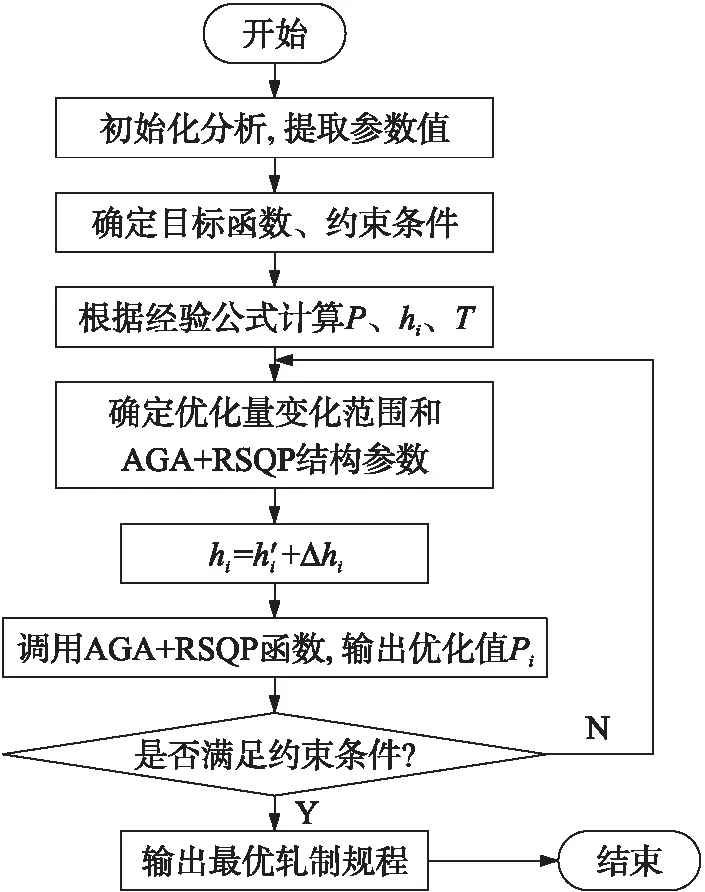
图3 优化轧制规程算法流程图

5 仿真结果分析

本文在某厂铝(1+4)热连轧机组上进行了验证,机组主要设备参数见表1。最终得到经验算法厚度分配值、其他参数分配值、未改进的MA及改进的MA的参数分配值,如表2所示。

结合表2,从等相对功率裕度和良好板形2个角度进行实验结果数据分析,分别给出h、ε和P参数分配的对比曲线,见图4。

表1 铝板带热连轧机组主要工艺参数表

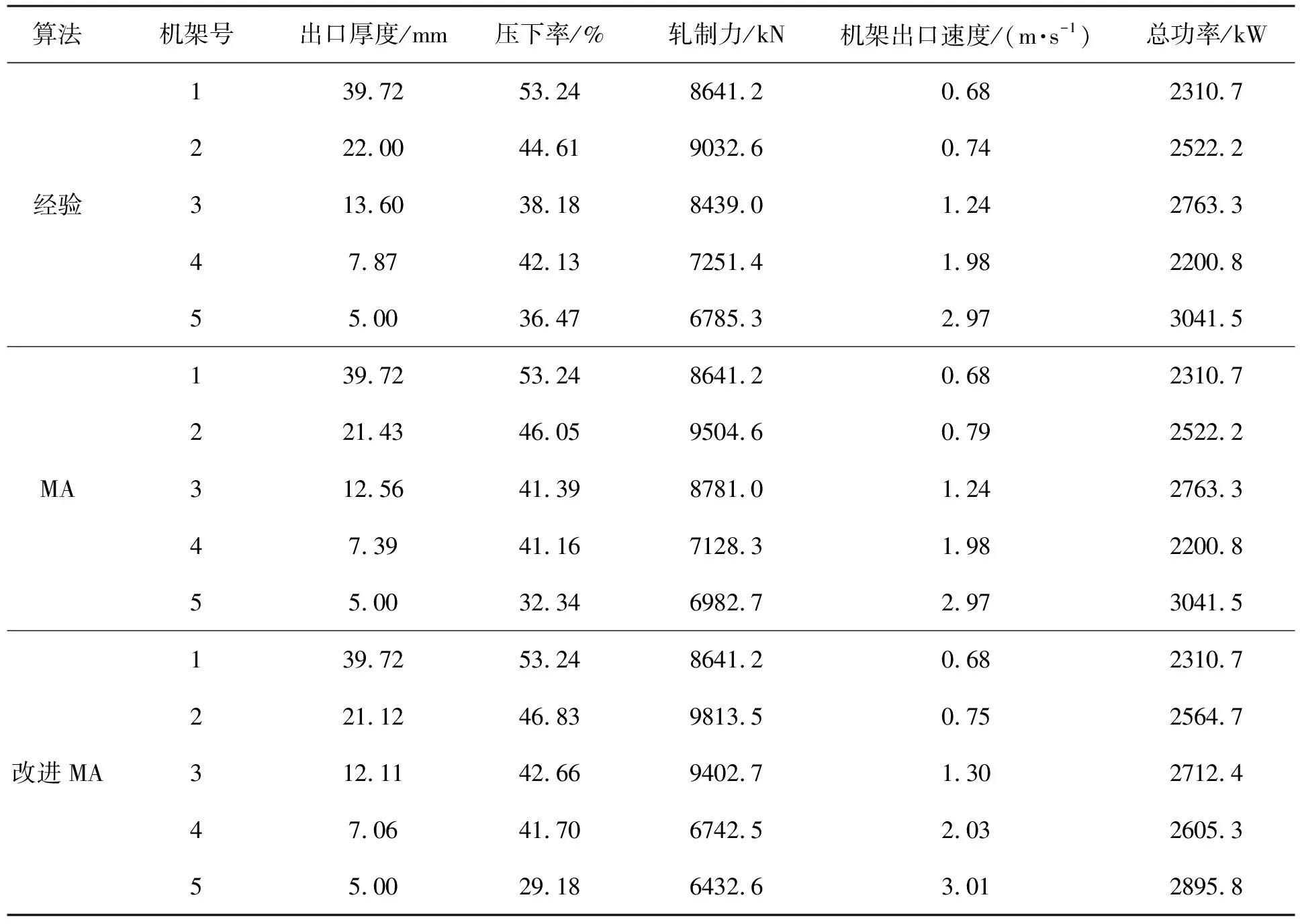
表2 各机架负荷分配方案表

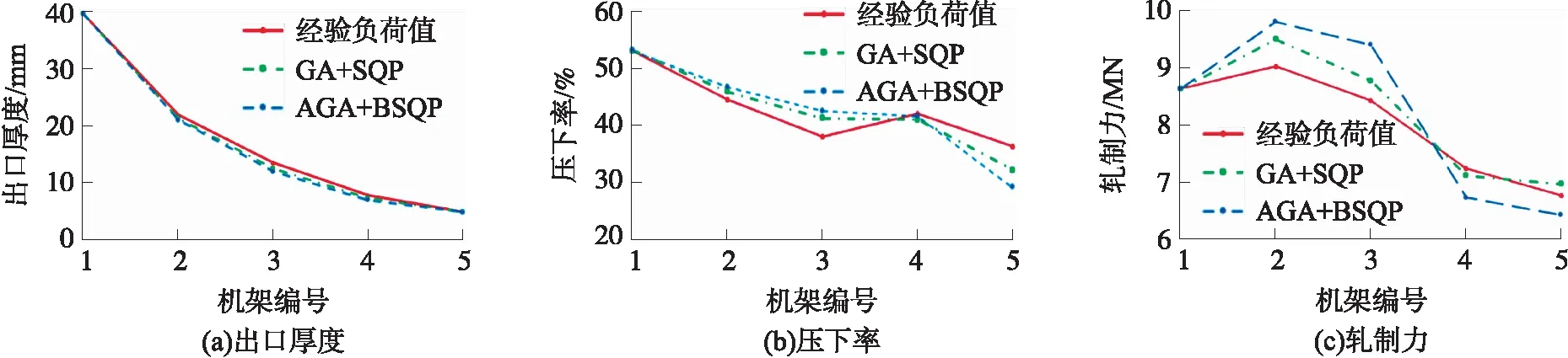
图4 参数分配对比曲线图

从表2方案的对比中可以看出,使用经验法不能实现均衡负荷目标,而经AGA+RSQP的MA优化之后,1～3机架充分利用热精轧机的高温轧制,达到了最大压下率,4～5机架逐步减小了轧制力P的预设值,这样能够保证铝板带材成品平整度、板形厚度精度等指标的实现。相对于经验算法负荷分配和GA+SQP算法的寻优效果,改进MA在负荷均衡和产品精度上都更高,经过仿真验证,AGA+RSQP算法优化的负荷分配更贴近优化目标且更加合理,同时增加了带材的平整度和板形精度,取得了较好的仿真效果。

本文在实验机组上应用了上述优化方案,从图5现场IBA软件系统分析图中可以看出,优化算法得到的轧制规程实现了机架间均衡的负荷分配,降低了终轧轧制力,最终成品质量提升了近10.8%。

图5 末机架厚差及板形二维记录图

6 结束语

本文采用改进MA对非线性目标函数和多约束条件的连轧轧制规程进行优化仿真。通过文化基因的外部框架算法AGA结合二次局部搜索的方法RSQP来进行负荷的均衡分配并获得良好的板凸度。AGA的进化操作使用自适应动态技术和改进操作算子等方法来弥补原GA算法的不足,改善了GA算法局部寻优能力差、容易早熟的问题。对SQP采用一阶校正步来降低其不可行程度,通过校正算法建立一阶可行下降方向,只求解总有可行解的1个二次规划函数,来提高SQP的全局收敛性,并减小计算量和存储量,增加了非线性约束问题的规模和算法的稳定性。仿真结果表明,本文改进MA有效提高了算法的收敛性和分布性,获得了更高质量的解集。最终通过实际生产进行了验证,结果证明基于改进的MA的铝热连轧轧制规程在等功率裕度负荷均衡和最终产品质量方面更为有效。