一种GPS/BDS/INS深组合导航系统降维滤波方法

刘 娣,朱松青,陈 桂,朱震曙

(1.南京工程学院 自动化学院,江苏 南京 211167;2.江苏金陵智造研究院有限公司,江苏 南京 210006)

卫星导航系统和惯性导航系统(Inertial navigation system,INS)由于高度的互补性,已经成为很多载体获取位置、速度和姿态信息的标准设备[1-5],如无人驾驶汽车使用卫星/INS组合导航系统提供车道级定位[6],列车采用全球定位系统(Globe position system,GPS)和INS相结合实现高精度定位[7]。根据信息融合的层次,卫星/INS组合导航系统可以归纳为松组合、紧组合和深组合导航系统[8,9]。松组合导航系统构建导航滤波器量测矩阵时,利用卫星导航系统和INS输出的位置和速度信息[9];紧组合导航系统采用伪距和伪距率差值构建量测矩阵,相对松组合系统而言,利用了更深层次的信息[10];深组合导航系统在紧组合系统的基础上增加了利用组合导航信息辅助卫星信号跟踪[11]。松组合导航系统没有涉及导航系统内部,仅单独使用卫星导航系统和INS输出的位置和速度信息,实现简单,计算量小。与松组合导航系统相比,紧组合和深组合系统采用伪距/伪距率构建量测信息,因此量测矩阵的维数和参与解算的卫星有关,更多的卫星参与解算会导致计算量“爆炸”。尤其是多星座系统,可能会有几十颗卫星参与解算,对于实时估计场景,需要在几ms以内完成组合导航滤波器的解算,这在量测矩阵维数爆炸的情况下是不可能完成的。

为了减少深组合导航系统计算量,通常采用联邦滤波的方法。Xie等[12,13]提出一种基于联邦滤波的方法,将每个星座对应的组合导航系统单独作为1个子滤波器处理,然后设置1个主滤波器完成信息的融合。然而每个子滤波器计算量并没有减少,单个星座的卫星数的增加会导致滤波器计算量增加。Luo等[14]提出一种预滤波的方法,利用多个并行的低维数滤波器来进行预处理,这样可以降低组合导航滤波器的更新频率,减少计算量,然而对于一些需要高速更新导航信息的场景,降低更新率具有一定的局限性。为了减少多星座卫星/INS深组合导航系统的计算量,本文以GPS/北斗卫星导航系统(Beidou navigation satellite system,BDS)/INS基于伪距/伪距率的深组合导航系统为例,提出一种降维的分散式组合导航滤波方法,在保证导航定位精度的同时,减少计算量,提高实时性。首先通过采用同一导航系统各通道之间的卫星伪距差分和伪距率差分的方法,消除时钟误差相关状态量,有效降低状态方程维数;再通过构建联邦滤波,将滤波方程分为2个子滤波器,降低量测矩阵维数;通过子滤波器的并行运行有效减少计算量。

1 集中式深组合系统模型

在单星座卫星/INS组合导航系统中,通常以卫星导航系统时钟误差和INS误差构建状态方程,以2个导航系统之间的伪距/伪距率差构建量测方程。当增加卫星星座时,最简单的处理方法是集中式组合方法(Centralized integration method,CIM),即在组合滤波的状态方程中增加相应的时钟相关状态量,在组合滤波的量测方程中增加相应的伪距/伪距率量测信息,通过主滤波器处理并估计状态,实现对惯性导航系统的误差补偿,达到抑制惯性导航系统发散的目的。

1.1 系统状态方程

在惯性导航系统误差基础上建立多星座卫星/INS深组合导航系统的状态方程,状态量增加了卫星导航系统的时钟误差项,包含系统时钟误差项的19维状态变量为X=[XIXGPSXBDS]T,XI为惯性导航系统对应的状态误差变量,XGPS和XBDS为GPS和BDS对应的时钟误差,XI、XGPS、XBDS具体形式如下

式中:φE、φN、φU为东、北、天姿态误差角;δvE、δvN、δvU为东、北、天速度误差;δL、δλ、δh为纬度、经度和高度误差;εx、εy、εz和▽x、▽y、▽z分别为惯性器件在载体坐标系下的陀螺随机漂移、加速度计偏置;δtb,GPS为GPS接收机时钟偏差;δtd,GPS为GPS接收机漂移;δtb,BDS为BDS接收机时钟偏差;δtd,BDS为BDS接收机漂移。

多星座GPS/BDS/INS组合滤波方程中的状态方程可表示为

(1)

即

(2)

式中:F为19×19阶的系统状态转移矩阵,G为19×10阶的系统噪声驱动阵,W为12维噪声向量。

1.2 系统量测方程

以GPS系统为例,伪距观测方程可表示为

(3)

式中

系统伪距率观测方程为

(4)

式中

(5)

eij为载体和对应的卫星之间的视线矢量;λ为经度;L为纬度。

BDS观测方程和GPS类似,综合式(3)～(5),可以得到多星座GPS/BDS/INS组合导航系统量测方程为

(6)

2 分散式组合导航方法

2.1 分散式滤波系统模型

在集中式组合导航滤波中,时钟误差量是每个卫星导航系统特有的,本文统一将卫星导航系统2个通道的伪距/伪距率量测值进行一次差分,抵消钟差和钟漂误差项的影响,达到减少状态方程维数的目的。

(1)基于伪距/伪距率差分的组合滤波方法状态方程。

式(1)中集中式深组合系统模型状态变量维数为19。相对于集中式方法,新模型的状态方程中去除了时钟相关误差项,状态向量为

δhεxεyεz▽x▽y▽z]T

系统状态方程如下

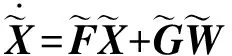
(7)

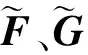
(2)基于伪距/伪距率差分的组合滤波方法量测方程。

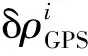
(8)

(9)

伪距差分方程

(10)

伪距差分观测方程为

(11)

式中

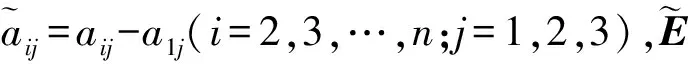
i=2,3,…,n;j=1,2,3

伪距率差分方程

(12)

伪距率差分观测方程为

(13)

式中

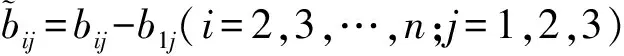
(14)

综上,新的观测方程可表示为

(15)

2.2 分散式组合导航方法分析

2.1节通过星间差分消除了时钟相关变量,降低了状态方程和量测方程的维数,本节进一步研究将滤波器分拆成多个子滤波器,通过分散估计、两步级联的方法减少计算量,即分散式组合方法(Decentralized integration method,DIM)。图1所示为联邦卡尔曼滤波器结构框图,其中包含GPS/INS组合子滤波器和BDS/INS组合子滤波器2个并行的子滤波器,两者均为卡尔曼滤波器,子滤波器同步向主滤波器提供局部估计信息;主滤波器实现对子滤波器状态估计信息的全局融合,并将结果反馈给各子滤波器。

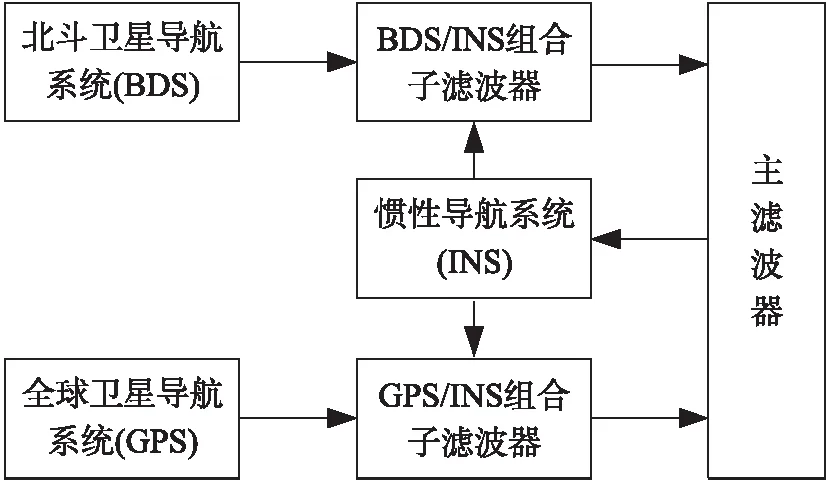
图1 联邦卡尔曼滤波器结构框图

(1)GPS/INS组合子滤波器。

(16)

(17)

(2)BDS/INS组合子滤波器。

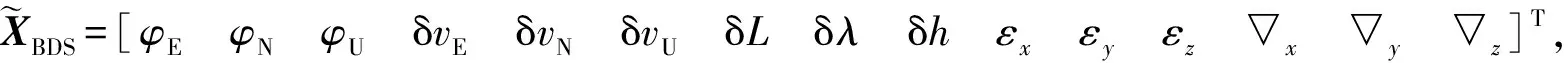
(18)

(19)

(3)主滤波器。

信息分配方法具体为:系统信息在主、子滤波器间的分配满足

βm+βGPS+βBDS=1

(20)

式中:βm、βGPS、βBDS分别为主、子滤波器信息分配系数。本文研究的分散式系统联邦滤波器中,主滤波器不进行信息分配,主滤波器仅对子滤波器估计信息进行全局融合并对子滤波器进行反馈,即

(21)

GPS/INS子滤波器和BDS/INS子滤波器信息分配系数阵βGPS和βBDS具体形式如下

(22)

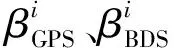
(23)

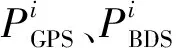
系统信息在子滤波器中的具体分配方法如下

(24)

主滤波器数据融合方法具体如下

(25)

3 系统仿真和算法性能分析

3.1 仿真实验

本文以卫星导航系统模拟器为信号源,对本文算法进行仿真分析,并与常规CIM方法进行性能对比。首先由卫星导航系统模拟器产生相应的GPS/BDS导航卫星信号,然后对中频信号数据进行采集,再由软件接收机对中频信号数据进行处理。轨迹数据来自于轨迹发生器。轨迹发生器能够模拟产生包括比力、陀螺仪角速率、位置、速度和姿态信息在内的惯性数据。构建多星座卫星/INS深组合导航仿真系统,对算法进行仿真分析。系统相关参数如表1所示,伪距、伪距率观测白噪声分别为15 m和0.1 m/s,组合导航卡尔曼滤波周期为1 s。

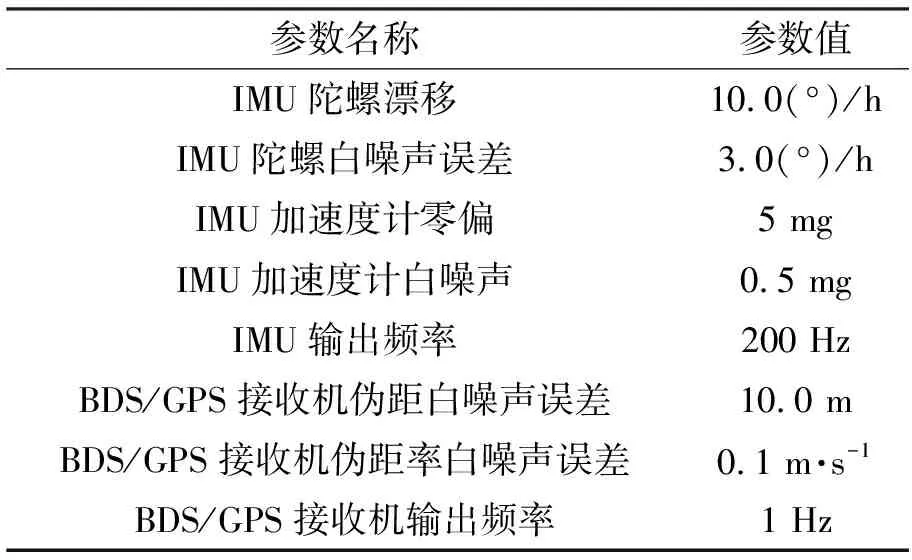
表1 组合导航系统参数表

仿真结果如图2～图4所示。图2表示单星座GPS/INS深组合导航系统、多星座GPS/BDS/INS深组合导航系统DIM方法和CIM方法在纬度、经度和高度的位置误差。表2为位置误差的均方根误差、方差以及平均值分析结果。分析可知,相比于单星座GPS/INS深组合导航系统,多星座GPS/BDS/INS深组合导航系统DIM方法具有更高的精度,其纬度、经度和高度的均方根误差分别减少了44.94%、27.27%和59.29%,方差分别减少了75%、47.44%和83.16%,平均值分别减少了37.17%、48.48%和57.39%。相比于CIM方法,DIM方法纬度、经度和高度的均方根误差分别减少了19.67%、5.88%和32.94%,方差分别减少了60%、10.87%和54.79%,平均值分别减少了22.83%、12.82%和11.76%。DIM方法纬度、经度和高度的位置精度相对于CIM方法有一定的提升。

图2 位置误差曲线图

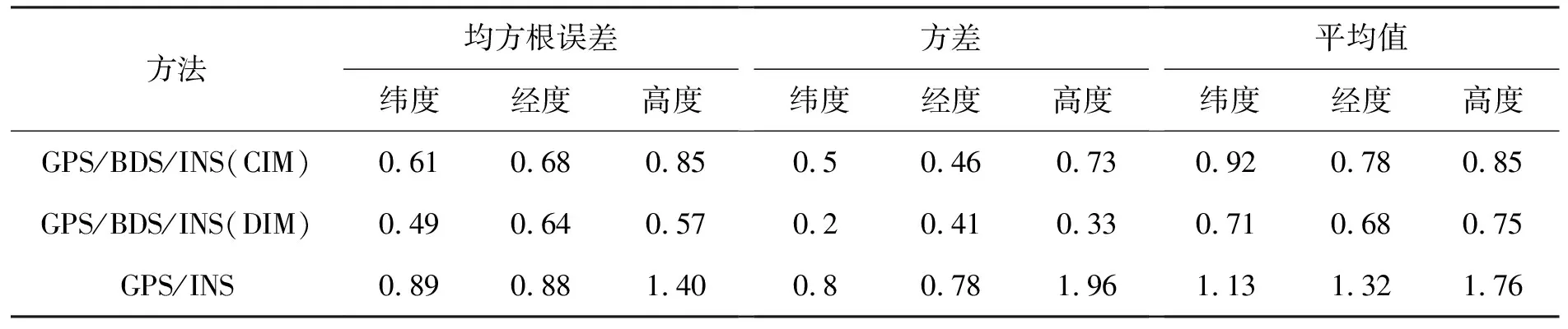
表2 位置误差数据统计分析表

图3为GPS/INS深组合导航系统、GPS/BDS/INS深组合导航系统DIM方法和CIM方法的东速、北速和天速误差曲线。表3为速度均方根误差、方差以及平均值分析结果。分析可知,相比于单星座GPS/INS深组合导航系统,多星座GPS/BDS/INS深组合导航系统DIM方法具有更高的精度,其东速、北速和天速均方根误差分别减少了23.53%、23.53%和16.67%,方差分别减少了23.81%、44.83%和22.22%,平均值分别减少了-11.18%、-17.65%和17.39%。相比于CIM方法,DIM方法东速、北速和天速的均方根误差分别减少了0%、7.14%和7.41%,方差分别减少了0%、5.88%和-14.29%,平均值分别减少了3.01%、0%和9.52%。DIM方法东速、北速和天速精度与CIM方法相当。

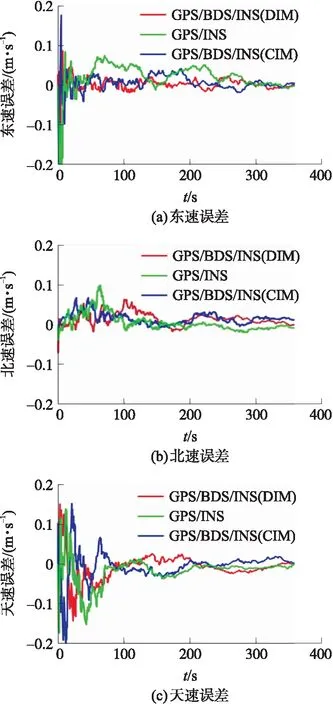
图3 速度误差曲线图

图4为GPS/INS深组合导航系统、GPS/BDS/INS惯性深组合导航系统DIM方法和CIM方法偏航角、俯仰角和滚转角误差曲线,误差分析结果如表4所示。分析可知,相比于单星座GPS/INS深组合导航系统,多星座GPS/BDS/INS深组合导航系统DIM方法具有更高的精度,其偏航角、俯仰角和滚转角均方根误差分别减少了59.26%、57.69%和40.74%,方差分别减少了77.36%、57.14%和23.94%,平均值分别减少了68.75%、62.50%和16.22%。相比于CIM方法,DIM方法偏航角、俯仰角和滚转角均方根误差分别减少了21.43%、-9.09%和30.43%,方差分别减少了40%、-8.33%和-50%,平均值分别减少了41.18%、-8.33%和-3.23%。DIM方法偏航角、俯仰角和滚转角精度与CIM方法相当。

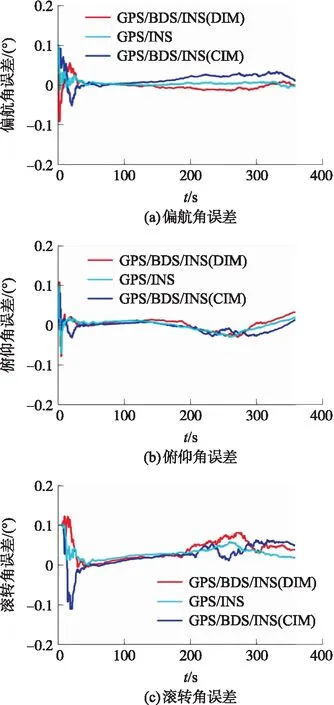
图4 姿态误差曲线图

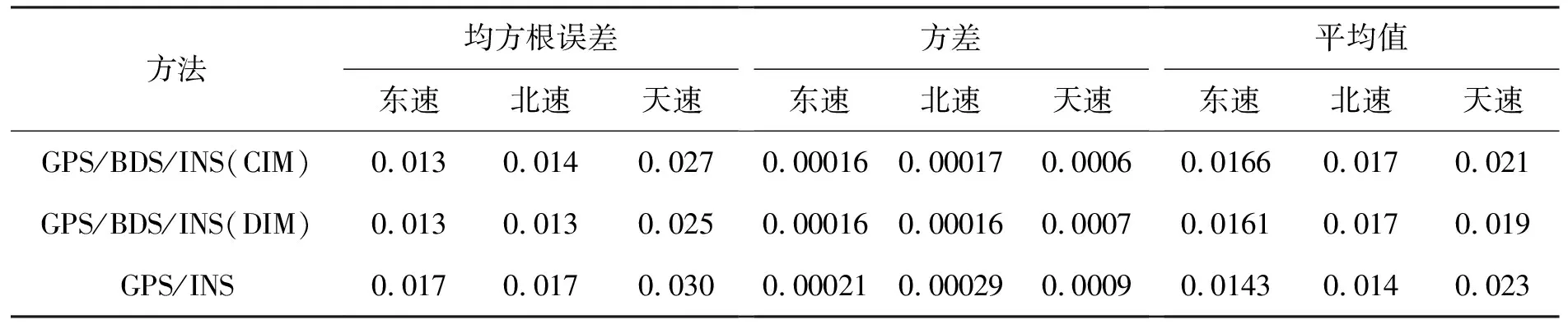
表3 速度误差数据统计分析表

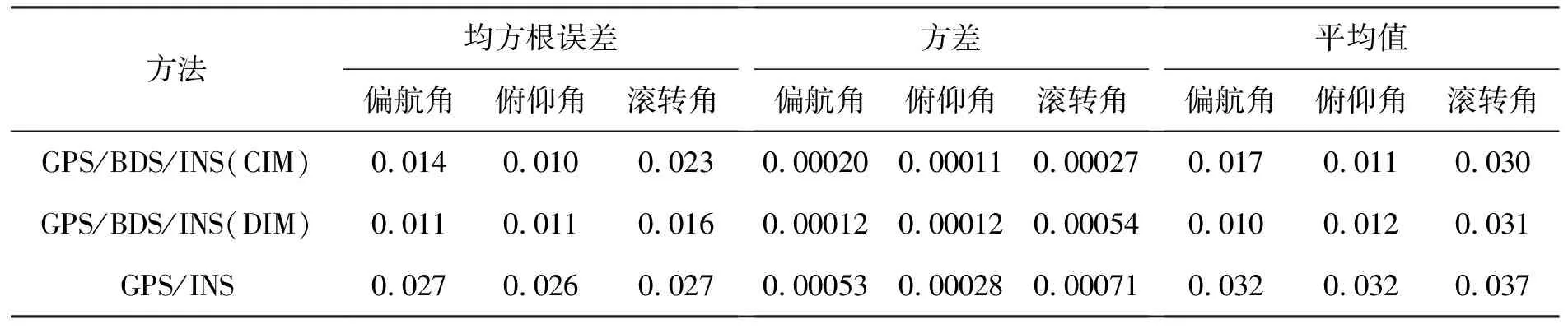
表4 姿态误差数据统计分析表

综合上述分析结果可看出,相对于单星座系统,本文多星座GPS/BDS/INS深组合导航系统精度有明显提高,DIM相比于CIM精度也有一定程度的提升,但由于分散式滤波采用分散估计、两步级联的分散化滤波方法,能有效降低计算量。

3.2 算法复杂度和计算量分析

根据3.1节分析可知,本文提出的多星座GPS/BDS/INS深组合导航系统DIM方法精度相对CIM方法精度有一定的提升,本节在Alienware笔记本(I7 CPU,16GB RAM)平台上,基于MATLAB2018软件仿真运行相关方法,对DIM方法和CIM方法的计算复杂度和计算量进行进一步分析。本文利用星间差分和联邦滤波的方法,将量测方程拆分成2部分分别计算。假设GPS和BDS可见星数目分别是m和n,表5列出了CIM导航滤波器、GPS/INS子滤波器、BDS/INS子滤波器相关矩阵维数变化的关系,可见相对于CIM导航滤波器,后两者的观测矩阵维数、观测方差阵维数、卡尔曼滤波增益矩阵维数都大大降低,由于卡尔曼滤波算法计算量和矩阵维数呈指数级关系,因此随着相关矩阵维数的增加,算法计算量将快速增加。滤波器100次仿真单次平均运行时间如表5所示,可以看出,当GPS和BDS可见星数目均为4时,DIM运行时间相对于CIM减少了大约31.7%;当GPS和BDS可见星数目均为5时,DIM运行时间相对于CIM减少了大约28.4%。这一方面是因为DIM相关矩阵维数较低,有效减小了计算量;另一方面,DIM的2个子滤波器可以并行运行,可有效减少运行时间。因此,DIM方法能在保证定位精度的前提下有效提高运行速度,更好地满足实时性要求高的应用场合。

表5 算法复杂度和计算量分析结果表

4 结束语

本文提出了一种基于星间差分和联邦滤波的分散式组合滤波器架构,解决了多星座GPS/BDS/INS深组合导航系统组合导航滤波器计算量大、实时性差的问题。不同于集中式组合导航滤波方法,本文在通过星间差分降低状态方程维数的基础上,进一步通过分散式滤波方法降低了量测方程的维数,有效减少了计算量。最后以GPS/BDS/INS深组合导航系统为例进行了仿真分析。实验结果表明,本文方法可以在保持定位精度的同时显著减少计算量,满足实时导航应用场景需求。