利用TI图形计算器对一道高考题的深入探究

广东省佛山市顺德区青云中学(528313) 蔡 斌

1 问题描述

题目(2020年高考全国I卷理科数学第20 题)如图1,已知A,B分别为椭圆E:+y2= 1(a ＞1)的左、右顶点,G为E的上顶点,=8,P为直线x=6 上的动点,PA与E的另一交点为C,PB与E的另一交点为D.

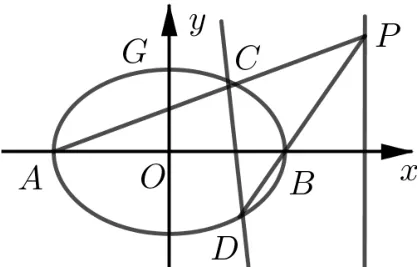
图1

(1)求E的方程;

(2)证明: 直线CD过定点.

2 解法探究

思路一由于直线CD随着点P的变化而变化,所以可以设P(6,m),则直线PA的方程是y=(x+3),直线PB的方程是y=(x-3),利用TI 图形计算器的CAS 运算功能直接求出直线CD所在的直线方程,然后确定定点,计算思路如下:

i.通过解方程组功能直接计算出C和D的坐标;

ii.给出直线CD两点式方程.(限于篇幅,过程从略.)由直线CD的方程可以知道直线CD恒过点

思路二由对称性可知若CD过定点,则该定点一定在x轴上,所以可以设直线的方程为x=ny+m,先求出C,D两点坐标,然后分别求出直线AC,BD的方程,最后求出P点坐标即可,利用P点横坐标为6 来确定m的值.

点评思路一和思路二思路自然,方法直接,比较容易想到,但运算量过大,尤其是思路二,用“笔算”几乎很难实现.但是只要我们有思路、设计好“算法”步骤,充分利用技术来完成“机械”的运算,也能够达到解决问题的目的,突破解析几何“会想不会算”这一难点.(限于篇幅,过程从略.)

思路三毕竟考试不能使用计算器,所以必须优化运算步骤,简化运算过程,达到“笔算”也能顺利完成的目的.通常的做法是利用“设而不求”的数学思想方法.

解析由对称性可知若CD过定点,则该定点一定在x轴上,所以可以设直线CD的方程为x=ny+m,由已知可得-3＜m ＜3,设C(x1,y1),D(x2,y2).联立椭圆E与直线CD的方程,得(n2+9)y2+2mny+m2-9 = 0.因为Δ=4m2n2-4(n2+9)(m2-9)＞0,所以

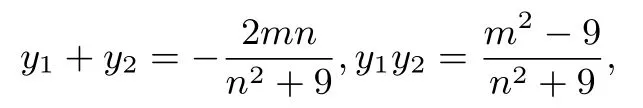
设P(t,6),则消去t得3y1(x2-3)=y2(x1+3),又因为y22=则3y1y2(x2-3)=y22(x1+3)=·(x1+3)即-27y1y2=(x1+3)(x2+3),将x1=ny1+m,x2=ny2+m代入得,(n2+27y1y2+(mn+3n)(y1+y2)+(m+3)2=0,即(n2+27)(m2-9)-(mn+3n)·2mn+(m+3)2(n2+9)=0,化简得2m2+3m-9 = 0,解得m=或m=-3(舍),所以直线CD恒过点

点评先利用对称性分析出定点在x轴上,再充分挖掘C,D所满足的代数条件,并用含y1+y2,y1y2的式子表示,最后利用韦达定理求出m的值,整个问题解决的过程中要求解题者不但有很好的运算能力,还要具有较高的逻辑推理素养.

3 拓展探究

3.1 原命题拓展

如果A,B分别为椭圆= 1(a ＞b ＞0)的左、右顶点,P为直线x=m(m /=±a)上的动点,PA与E的另一交点为C,PB与E的另一交点为D,那么直线CD还过定点吗?

几何直观验证: 借助TI 图形计算器的滑动条及动态绘图功能进行探究,如图2 所示,改变m的值,直线CD恒过定点;同理,可以观察到当椭圆焦点在y轴上时,相应的结论仍然成立.这启发我们证明如下的

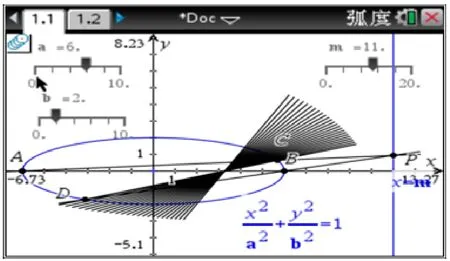
图2

性质1已知A,B分别为椭圆= 1(a ＞b ＞0)的左、右顶点,P为直线x=m(m /=±a)上的动点,PA与E的另一交点为C,PB与E的另一交点为D.直线CD恒过定点

证明可以设P(m,t),则直线PA的方程是y=(x+a),直线PB的方程是y=(x-a),利用TI 图形计算器的CAS 运算功能,经过如下的步骤:

i.联立椭圆与直线的方程分别求出点C,D的坐标;

ii.写出直线CD的方程;

iii.化简直线CD的方程,得出CD通过定点(限于篇幅,过程从略.)

直接求出直线CD所在的直线方程,然后确定定点,计算过程如下:

3.2 重组命题的条件和结论,探究逆命题是否成立

已知A,B分别为椭圆E:= 1(a ＞b ＞0)的左、右顶点,C,D为椭圆上不同于顶点的两点,若CD过定点(m,0)(不为原点),则直线AC与直线BD的交点P的轨迹是否为垂直于x轴的直线呢?

几何直观验证: 我们再次借助TI 图形计算器的滑动条及动态作图功能,观察满足条件的两直线AC与BD的交点的变动情况,如图3,由此启发我们证明如下的性质

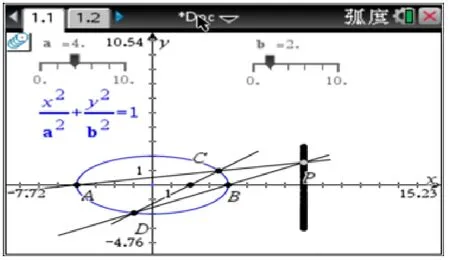
图3

性质2已知A,B分别为椭圆= 1(a ＞b ＞0)的左、右顶点,C,D为椭圆上不同于顶点的两点,若CD过定点(m,0)(不为原点),则直线AC与BD的交点P在定直线x=上.

证明可以设直线CD的方程为x=ky+m,并设C(x1,y1),D(x2,y2),则可以借助TI 计算器:

i.分别给出AC的方程及BD的方程;

ii.求出如上两直线交点P的坐标.

据如上两步骤,推出点P的横坐标始终为定值即P点的轨迹为直线x=(限于篇幅,细节从略.)

3.3 更改条件,重组开放性问题

若A,B为椭圆E:=1(a ＞b ＞0)左右顶点,C为E上任意异于A,B的点,则有kCA·kCB=在拓展1 中,又因为所以kCB ·kBD=即直线CB与BD的斜率之积为定值.于是可以探究下列问题:

已知A为椭圆= 1(a ＞b ＞0)的左顶点,B,C为椭圆上的两点,直线AB与直线AC的斜率为k1,k2,若k1k2=m,则直线BC过定点吗?

几何直观验证,如图4 所示,通过探究发现,当k1k2为定值时,直线BC过定点.这启发我们给出如下的性质

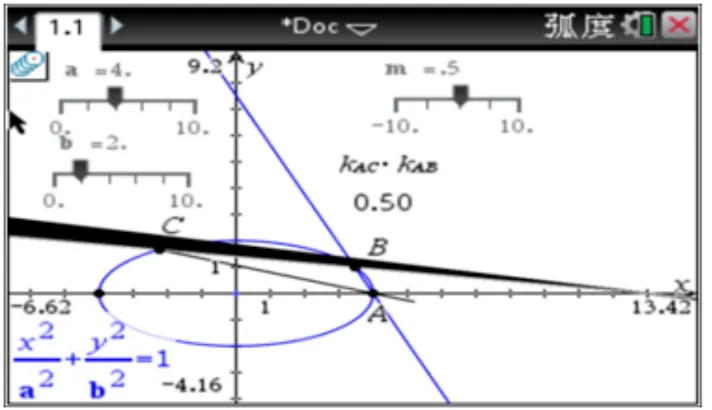
图4

性质3已知A为椭圆E:= 1(a ＞b ＞0)的左顶点,B,C为椭圆上的两点,直线AB与直线AC的斜率分别为k1,k2,且k1k2=m(其中m/=则直线BC恒过定点

证明设直线AB的方程为y=k1(x-a),AC的方程为(x-a),则利用TI 图形计算器:

i.通过联立椭圆与直线的方程,分别求出B,C的坐标;

ii.写出直线BC的方程.

由此得到,直线BC恒过点(其中

特别地,通过探究发现当m=时,直线BC平行于x轴,当m=时,直线BC恒过原点,如图5 所示:

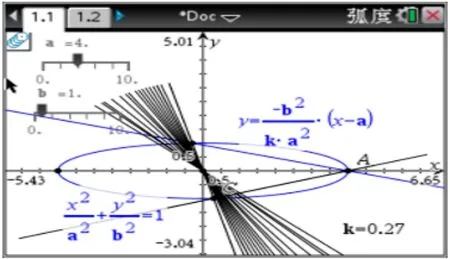
图5

通过探究发现,性质3 的逆命题也成立

性质4A为椭圆E:= 1(a ＞b ＞0)的左顶点,过定点M(m,0)的直线l与椭圆相交于B,C两点(都不与A重合),记直线AB与直线AC的斜率分别为k1,k2,则k1·k2为定值,且k1·k2=

3.4 条件变式,重组开放性问题

已知A分别为椭圆E:= 1(a ＞b ＞0)的左顶点,B,C为椭圆上的两点,直线AB与直线AC的斜率为k1,k2,若k1+k2=m(其中m/=0)则直线BC过定点吗?

几何直观验证: 如图6,通过探究发现,当k1+k2为定值时,直线BC过定点.

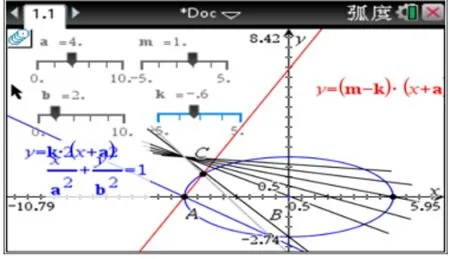
图6

性质5已知A为椭圆E:=1(a ＞b ＞0)的左顶点,B,C为椭圆上的两点,直线AB与直线AC的斜率分别为k1,k2,且k1+k2=m(其中m /= 0),则直线BC恒过定点

证明设直线AB的方程为y=k(x-a),则AC的方程为y=(m-k)·(x-a),则利用TI 图形计算器计算,可以得到直线BC恒过定点(限于篇幅,细节从略.)

对于斜率之商和斜率之差为定值的情形也可以类似探究,这里不在赘述.

4 题源探究

性质2 反应了椭圆上存在的一个定点与定线问题的几何性质,那么这一性质能够推广到更一般的情形呢? 通过探究发现: 过定点P的两条动直线AB,CD分别于椭圆相交A,B,C,D四点,则直线AC与BD的交点在一条定直线上,如图7 所示.

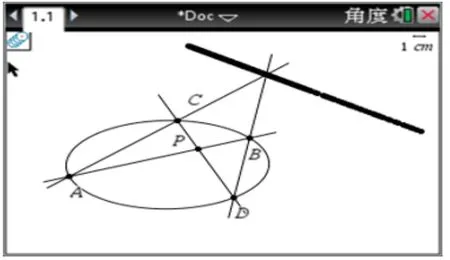
图7

上面中椭圆的性质实质上是有关圆锥曲线的极点极线理论,其中点P和直线AC与BD的交点所在定直线为椭圆的一对极点和极线,相关知识可参考文献[1],而2020年的这道高考解析几何试题实际上是文[1]中有关极点极线的一个命题:

命题[1]若椭圆的方程为= 1(a ＞b ＞0),则点P(x0,y0)和直线= 1 为椭圆的一对极点和极线.

利用这一命题来解这道高考题,已知直线x= 6 为椭圆+y2=1 的一条极线,设它所对应的极点为P(x0,y0),则直线= 1 与x= 6 重合,故x0=,y0= 0.则CD恒过的定点就是极线x=6 为所对应的极点

5 探究体会

5.1 技术运用对数学教学与数学学习的影响

本探究案例中,借助TI 图形计算器强大的动态绘图和CAS 运算功能,对数学问题进行拓展探究,只要我们有了想法就能快速作图进行验证,深入下去.当通过作图分析获得直观结论后,再利用超强的CAS 运算系统进行代数证明,大大地提高了运算效率,尤其对那些运算能力欠缺的学生,也能顺利完成探究任务,这在传统的教学中是不可能实现的.

5.2 技术运应突出数学的思考

数学学习主要目的是通过学生在解决数学问题的过程中提升自身的思维能力,而借助技术能使得抽象问题具体化、动态化和形象化、这样不但能拓展学生的思维,还能帮助学生深入理解问题的本质.同时,把繁琐“机械”的运算交给机器完成,让学生有更多的时间进行数学的思考,这也符合新课标的要求.在本探究案例中,正是有了理性的分析和逻辑推理,才能更好地让技术服务于我们的数学学习.