直观想象在2021年高考适应性考试中的应用分析

华南师范大学数学科学学院(510631) 杨宇佳

1 背景

纵观2021年高考适应性数学考试试题,依旧本着“考察数学理性思维和探究能力,注重运用数学思想和通性通法解决问题”的原则来进行命题.试题整体的综合性和创新性较高,对学生获取新知识,探究新问题的能力要求也显著提升.同时,试题也反映了新课程改革的精神,数学知识考察的范围越来越广,要求培养的创新意识也越来越强,为后期新高考的准备与复习提供了一些新的方向与启发.试题中多次考查学生的直观想象的素养: 建立数与形之间的关系、利用几何图形描述问题、借助几何直观理解问题、运用空间想象认识事物,都是在考查学生能否灵活运用直观想象来思考和解决问题.

2 数学核心素养之直观想象的含义

直观想象是指借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形,理解和解决数学问题的素养.主要包括: 借助空间形式认识事物的位置关系、形态变化与运动规律;利用图形描述、分析数学问题;建立形与数的联系,构建数学问题的直观模型,探索解决问题的思路.直观想象是发现和提出问题、分析和解决问题的重要手段,是探索和形成论证思路、进行数学推理、构建抽象结构的思维基础.要培养学生直观想象的能力,也就是要提升数形结合的能力,发展几何直观和空间想象能力;增强运用几何直观和空间想象思考问题的意识;形成数学直观,在具体的情境中感悟事物的本质.

3 2021年高考适应性数学考试试题分析

3.1 建立形与数之间的联系

“数形结合”是中学数学常用的解题方法,能把抽象的数学语言、数量关系和直观的几何图形、位置关系联系起来,既可以通过“用形助数”,也可以通过“以数解形”来解决问题.这是一种抽象思维与形象思维的结合.数形结合往往能够使复杂的问题变得简单,使抽象的问题变得具体,从而使问题容易被解决.

例1(2021年高考适应性考试第4 题)椭圆+= 1(m ＞0)的焦点为F1,F2,上顶点为A,若∠F1AF2=则m=( )

解析a2=m2+1,b2=m2,则c2=a2-b2=1,由题意根据图像(图1)可迅速得知:b=则b2= 3c2= 3 =m2,又因为m2＞0,所以m=故答案为C.

图1

评注这道题考察的是圆锥曲线的知识,解决问题的重点在于“椭圆方程的待定系数之间的关系”和“等边三角形的性质”,考生可以通过画图来进行直接观察,利用图像即可较快得到数值之间的关系,相对比较简单.

例2(2021年高考适应性考试第7 题)已知抛物线y2= 2px上三点A(2,2),B,C,直线AB,AC是圆(x-2)2+y2=1 的两条切线,则直线BC的方程为( )

A.x+2y+1=0 B.3x+6y+4=0

C.2x+6y+3=0 D.x+3y+2=0

解析如图2,将A(2,2)代入y2= 2px可得p= 1,由于圆的切线与圆心的距离即为半径,可计算得直线AB的方程为+ 2 = 0,直线AC的方程为-2 = 0,联立直线方程和抛物线方程即可得B点和C点的坐标,则直线BC的方程即可求得为3x+6y+4=0.故答案为B.

图2

评注此题利用“数形结合”可以较快得到所需直线方程的解法,若学生能够充分发挥直观想象,在脑海中大致勾勒此图中直线与圆的位置关系,也可以省去画图的步骤,直接进行求解,相对比较简单.

例3(2021年高考适应性考试第14 题)若正方形一条对角线所在直线的斜率为2,则该正方形的两条邻边所在直线的斜率分别为____,____.

解析如图3,可将正方形放入直角坐标系中,设O(0,0),A(1,2),则可知B(-2,1),D(2,-1),所以kAB=

图3

评注此题题目中直接给出了“几何图形”——正方形,学生可以画出相应的正方形,根据图形间的关系利用三角函数直接进行求解.但题目中涉及求斜率问题,若将几何图形放入直角坐标系中,利用数形结合的方法,则能够大大减少计算量,在考场上节约时间.

例4(2021年高考适应性考试第21 题)双曲线C:= 1(a ＞0,b ＞0)的左顶点为A,右焦点为F,动点B在C上,当BF⊥AF时,|AF|=|BF|.

(1)求C的离心率;

(2)若B在第一象限,证明: ∠BFA=2∠BAF.

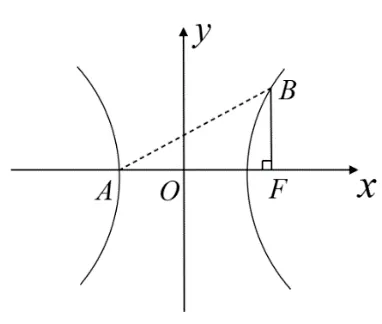
图4(1)

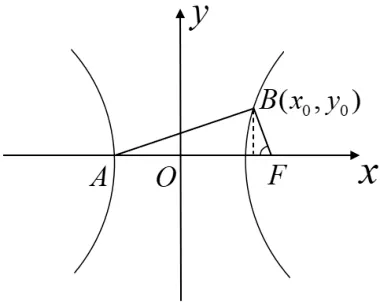
图4(2)

解(1)当BF⊥AF时,BF=所以a+c=a2+ac=c2-a2,(e-2)(e+1)=0,e=2.

(2)= 2,c= 2a,可知双曲线C的方程为C:=1(a ＞0).不妨设B(x0,y0),则:

①当x0=c时,|AF|=|BF|,此时ΔBAF为等腰直角三角形,∠BFA==2∠BAF显然成立.

②当a ＜ x0＜ c时,要证∠BFA= 2∠BAF,只需证tan ∠BFA= tan(2∠BAF),其中tan 2∠BAF=即只需证上式通过化简可得2(ax0-x20+2a2)=-2x20+2ax0+4a2,此式显然成立,因此tan ∠BFA= tan(2∠BAF)成立,又因为∠BFA和2∠BAF均为锐角,因此∠BFA=2∠BAF成立.

③当x0＞c时同②可证∠BFA= 2∠BAF成立.综上所述,∠BFA=2∠BAF得证.

评注此题仍然考察圆锥曲线的知识,但考察的却是历年较少关注的双曲线的内容.第一问可以根据题目的数据直接计算得知,但第二问则需要动动脑筋,现已知点所在的象限,要求证角与角之间的数量关系,由于涉及到角的大小和双曲线的性质,直接计算往往比较困难,而这时若采用图像来观察,则可以有效快捷的提供解题的思路与方法,也能帮助学生发现此题要利用分类讨论的方法来解决.

3.2 借助几何直观理解问题

“几何图形”是学生在学习过程中常遇到的事物,其往往能够直观的展示量与量之间的关系.学生所接触到的大多抽象的数学问题,其数学本质均可以用直观的几何图形来表达.“几何直观”是指利用图形描述和分析问题,即通过几何图形对事物进行的直接感知和整体把握,它能将不容易掌握的数学问题转化的更为具体化、简单化和形象化,有利于寻找化解问题的思路与方式.

例5(2021年高考适应性考试第18 题)在四边形ABCD中,AB//CD,AD=BD=CD=1.

(1)若AB=求BC;

(2)若AB=2BC,求cos ∠BDC.

解(1)如图5,过点D做DE⊥AB于点E,可得BE=由AB//CD可知cos ∠BDC= cos ∠EBD=根据余弦定理可知BC2=DB2+DC2-2DB·DC·cos ∠BDC,因此BC=

图5

(2)不妨设BC=x,则AE=BE=BC=x,根据余弦定理,有= cos ∠BDC=cos ∠EBD=BE=x,化简 可得x=则cos ∠BDC=

分析该题仅给出了四边形的边之间的数量以及位置关系,通过凭空想象很难构造出题目描述的几何图形,但是学生可以根据题目要求尝试画出图形,找好四边形的边的位置关系和数量关系,就可以通过直观的几何图形进行分析,同时,在几何图形中构造辅助线求解问题也更加方便.

图6

例6(2021年高考适应性考试第20 题)北京大兴国际机场的显著特点之一是各种弯曲空间的运用.刻画空间的弯曲性是几何研究的重要内容.用曲率刻画空间弯曲性,规定: 多面体顶点的曲率等于2π与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),多面体面上非顶点的曲率均为零,多面体的总曲率等于该多面体各顶点的曲率之和.例如: 正四面体在每个顶点有3 个面角,每个面角是所以正四面体在各顶点的曲率为2π-3×=π,故其总曲率为4π.

(1)求四棱锥的总曲率;

(2)若多面体满足: 顶点数-棱数+面数= 2,证明: 这类多面体的总曲率是常数.

解(1)由题中定义可知多面体的总曲率= 2π×顶点数-各面的内角和,对于四棱锥来说,其有5 个顶点,4 个三角形面和1 个四边形面,因此四棱锥的总曲率=5×2π-(4×π+2π)=4π.

(2)不妨假设此类多面体的顶点数为x,棱数为y,面数为z,则有x-y+z= 2,同时,注意到多面体的每一条棱都相邻两个面.这时我们假设多面体的第1 个面有i1条棱,第2 个面有i2条棱,…,第z个面有iz条棱,则可以得到i1+i2+...+iz= 2y.此时利用“多边形的内角和= (边数-2)π”和“多面体的总曲率= 2π×顶点数-各面的内角和”,可以得到:

因此此类多面体的总曲率为一常数4π.

分析此题是考查立体几何的新定义题目,完全颠覆了固有的形态,直接给学生关于曲率的定义,然后根据定义做题,题目比较新颖,需要学生认真审题及理解题意.其中多面体的曲率的定义相对来说较难理解,学生可以通过画出正四面体进行直观的观察,再对比四棱锥的几何图形,根据其各面的形状、棱数、面数等数据进行概括总结,通过几何直观找到该题的突破口.第二问的证明则需要学生具有更高的数学素养,其中重难点在于观察到多面体的每一条棱都相邻着两个面,也就是说,在计算每个面的棱数并求和时,每条棱都被计算了两次,这是此题突破的难点,学生可以通过对正四面体和四棱锥的观察得到这个结论.

3.3 运用空间想象认识事物

“空间想象”是一种对空间几何形体进行观察、分析、认知的抽象思维能力.学生在立体几何的学习中,若空间想象能力强,则对学习有较大的帮助.由于学生在空间想象时,其思维要经历一个从二维到三维再到二维的转变,因此,通过空间想象可以培养和锻炼学生的空间感知能力,同时也能提高他们对空间几何体位置的判断能力.

例7(2021年高考适应性考试第11 题)下图(图7(1))是一个正方体的平面展开图,则在该正方体中

图7(1)

A.AE//CDB.CH//BEC.DG⊥BHD.BG⊥DE

解析将正方体的平面展开图进行还原,可得图7(2).在图中显然可知AE⊥CD,CH//BE,故A 错误,B 正确.在图中连接CH,易知CH⊥DG,CH ∩BC=C,所以DG⊥平面BCH,因此DG⊥BH,故C 正确.在图中连接AH,根据正方体的性质知AH//BG且AH⊥DE,因此BG⊥DE,故D 正确.

图7(2)

评注该题是典型的利用空间想象求解的问题.学生要根据已知的正方体的平面展开图以及各点的位置,借助空间想象,判断展开前的正方体的各顶点分别对应展开图中的哪些点,然后再根据还原的正方体对每个选项进行逐一判断.

例8(2021年高考适应性考试第13 题)圆台上、下底面的圆周都在一个直径为10 的球面上,其上、下底面半径分别为4 和5,则该圆台的体积为____.

解析该球的直径为10,半径为5,圆台的下底面半径恰好为5,所以圆台的下底面恰为球的直径所在平面.如图8 所示,OA=OD= 5,在三角形OO′A中,∠OO′A=因此根据勾股定理得OO′2=OA2-O′A2.因此OO′=3.根据圆台得体积公式V=计算可得该圆台的体积为61π.

图8

分析此题考察“圆台的体积与外接球”的知识,学生需要根据题意,利用空间想象能力,判断三维空间中圆台与球之间的位置关系,同时,学生要将三维物体转化到二维平面,利用解三角形的知识,得到圆台的高度,从而利用圆台的体积公式进行求解.

4 直观想象在适应性数学考试中的应用分析总结

通过以上试题分析可知,直观想象素养在高考中考察的比重较大,且未来可能会出现更广的应用以及出现更多新题型.而这就要求学生在学习的过程中,要提升数形结合的能力,发展几何直观和空间想象能力;增强运用几何直观和空间想象思考问题的意识;形成数学直观,在具体的情境中感悟事物的本质.为此,教师在日常教学和命题中,应当把握学生的培养规律,积极创造能够运用几何直观素养解决问题的情境,发挥学生的主体性,让学生在接受学习与发现学习中交叉感悟直观想象,使其在遇到数学问题时,能及时想到用几何化的图形去理解和探索问题,逐渐形成良好的直观想象素养.