追本溯源 回归教材——谈新高考数学复习的几点思考

深圳高级中学(集团)东校区(518118)张培兰

新高考试行以来,山东海南先行,新八省联考紧跟其后,为我们复习备考提供了一些新的方向和启发.

一、新高考及新八省适应性考试试卷分析

1.基于核心素养的命题原则,突出理性思维,考察关键能力

纵观2020 新高考试题和八省模拟演练数学试题,可以发现两大特点.一是围绕数学核心素养,突出数学通性通法,淡化解题技巧,关注数学的本源性问题,关注蕴含数学概念和思想方法的有意义问题.二是试题均体现了秉承素养导向、能力为重的原则下,突出考查学生的理性思维和探究能力,彰显了综合运用数学思想方法、发展“四能”的意识.将数学关键能力与理性思维、数学应用、数学探究、数学文化等学科素养统一在理性思维的主线上,在数学应用、数学探究等方面突出体现了理性思维和探究能力等关键能力的考察.

2.结构创新,力争打破形式套路

结构形式上有所创新,从12 道单选题变为8 道单选题和4 道多选题,多选题又从漏选得3 分变为得2 分;出现了逻辑题、数据分析题;填空出现双空题、开放性试题、举例题;阅读材料题、数学文化题可能出现在选择题,填空题甚至解答题.通过调整试卷结构,打破固有模式,探索试题排序方式和考核方法,努力打破原来复习备考中题海战术和套路训练的影响.此外,不仅在结构形式上创新,在内容、解法及结论上均有可能创新.

3.试题创新基于问题情境和数学文化背景

近两年的数学高考题文字量增多,阅读量大大提升,有点像“考语文”.这体现了课标在命题建议中提出的: 命题时,应有一定数量的应用问题,还应包括开放性问题和探究性问题,重点考察学生的思维过程、实践能力和创新意识,问题情境的设计要合理.[1]在命题中,选择合适的问题情境是考察数学核心素养的重要载体,情境包括现实情境、数学情境和科学情境.情境可以来自于现实生活,数学文化背景,数学问题情境的变式以及跨学科融合.这是试题内容创新的途径之一.

二、新八省联考、高考与教材的联系

每逢高考改革,学生就认为高考数学更难.但这种难,有时候不是数学真的难,而是在于“新”.“新”对于习惯题海战术,靠刷题、靠背套路的学生而言,就意味着各种变数和不确定性.正是这种对未知数的恐惧和不适应,学生认为难.但其实不管怎么变化,仔细研究试卷,便可发现很多知识点是相互贯通的,甚至是有所依托,有迹可循的.

这个依托就是我们的教材.市面上的教辅资料甚多,大多版面制作精美,把知识点、考点、题型分门别类,整理完善.这导致了很多老师舍本逐末,忘记了根本,弃教材于不顾,忽略知识的产生过程,一不小心就带领学生走上了刷题的道路.八省联考题目的设置,恰巧就踩在这个“痛点”上.其实,仔细研究试题可以发现,虽然内容形式上有所创新,但是题目内容始终离不开教材和课程标准.例如:

例1(2021年八省适应性考试第6 题)(1+x)2+(1+x)3+···+(1+x)9的展开式中x2的系数是( )

A.60 B.80 C.84 D.120

对接教材 (人教A 版选修2-3: 1.2.2 组合探究与发现:组合数的两个性质)

性质 1.Cmn=Cn-mn; 2.Cmn+1=Cmn+Cm-1n.

(人教A 版选修2-3: 第一章复习参考题B5)

在(1+x)3+(1+x)4+...+(1+x)n+2的展开式中,含x2项的系数是多少?

八省适应性考试第6 题,学生们可以列式计算C22+C23+···+C29的值,不过大部分是一个一个算累加起来的.若学生知道教材对应的探究,利用性质:Cmn+1=Cmn+Cm-1n,就会发现可以减少很多计算量,也可以解决n更大的情况:C22+C23+···+C29=C33+C23+···+C29=C34+C24+···+C29=C310.

例2(2021年八省适应性考试第17 题)已知各项都为正数的数列{an}满足an+2=2an+1+3an.

(1)证明: 数列{an+an+1}为等比数列;

(2)若a1=,求{an}的通项公式.

对接教材 人教A 版必修5: P32,阅读与思考: 斐波那契数列

(人教A 版必修5: 习题2.1B 组3)已知数列{an}的第一项是1,第2 项是2,以后各项由an=an-1+an-2(n ＞2)给出.

(1)写出这个数列的前5 项;

(2)利用上面的数列{an},通过公式bn=构造一个新的数列{bn},试写出数列{bn}的前5 项.

很多同学处理八省适应性考试第17 题是,联想到累加法,自创“累减法”.实际上这道题可以通过隔项分奇偶实现累加法.其次,学生很少接触或者几乎没有接触到相邻两项的和的类型.实际上教材的斐波那契数列就是个很好的载体.

例3(2021年八省适应性考试第20 题)北京大兴国际机场的显著特点之一是各种弯曲空间的运用.刻画空间的弯曲性是几何研究的重要内容.用曲率刻画空间弯曲性,规定: 多面体顶点的曲率等于2π与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),多面体面上非顶点的曲率均为零,多面体的总曲率等于该多面体各顶点的曲率之和.例如: 正四面体在每个顶点有3 个面角,每个面角是所以正四面体在各顶点的曲率为2π-3×=π,故其总曲率为4π.

(1)求四棱锥的总曲率;

(2)若多面体满足: 顶点数-棱数+面数= 2,证明: 这类多面体的总曲率是常数.

对接教材 如图: (新教材必修第二册第八章立体几何复习参考题的第一题)欧拉公式:

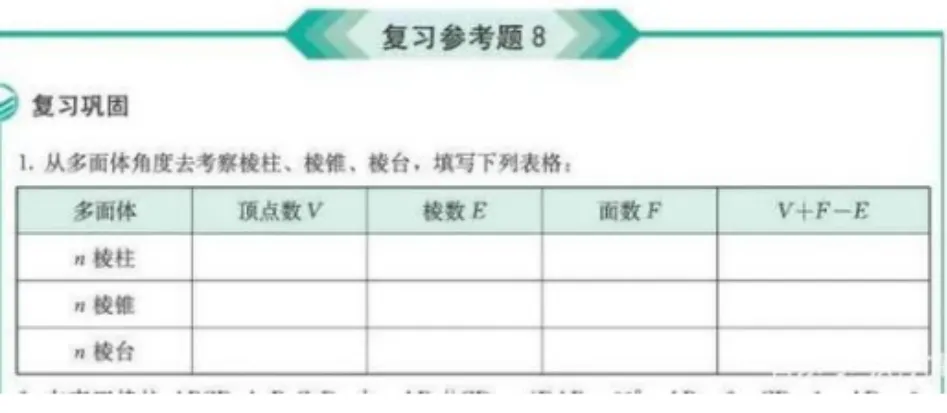
多边形的内角和是几何学的一个基本问题,人教版《数学(八年级上册)》(第21 页)第11 章§11.3.2 的标题即为:“多边形的内角和”也有相关知识.

从上面的例题可以看出,这几个题目出的题目相对新颖,学生乍看之间可能反应不过来,但是题目其实都来自于课本的阅读材料、探究与思考以及课后习题.

除了来自于教材,还有不少题目可以在历年高考题中找到踪迹.例如:

例4(2021年八省适应性考试第3 题)关于x的方程x2+ax+b=0,有下列四个命题: 甲:x=1 是该方程的根;乙:x= 3 是该方程的根;丙: 该方程两根之和为2;丁: 该方程两根异号.如果只有一个假命题,则该命题是( )

A.甲 B.乙 C.丙 D.丁

对接高考 (2019年高考全国II 卷文科第5 题)在“一带一路”知识测验后,甲、乙、丙三人对成绩进行预测.

甲: 我的成绩比乙高.乙: 丙的成绩比我和甲的都高.丙:我的成绩比乙高.

成绩公布后,三人成绩互不相同且只有一个人预测正确,那么三人按成绩由高到低的次序为( )

A.甲、乙、丙 B.乙、甲、丙 C.丙、乙、甲 D.甲、丙、乙

以上两题均是逻辑推理题,对于考全国一卷的同学而言,如果没有做全国II 卷这道题目,就会不适应,忙了阵脚.

例5(2021年八省适应性考试第21 题)双曲线C:= 1(a ＞0,b ＞0)的左顶点为A,右焦点为F,动点B在C上.当BF⊥AF时,|AF|=|BF|.

(1)求C的离心率;

(2)若B在第一象限,证明: ∠BFA=2∠BAF.

对接高考 (2018年高考全国I 卷理科第19 题)设椭圆C:+y2= 1 的右焦点为F,过F的直线l与C交于A,B两点,点M的坐标为(2,0).

(1)当l与x轴垂直时,求直线AM的方程;

(2)设O为坐标原点,证明: ∠OMA=∠OMB.

学生一看解答题居然出现双曲线,纷纷询问自己老师,不是说不考双曲线的吗? 为什么双曲线考的这么难.第一,这反映出刷题带来的固定局限思维;第二,对比2018年全国1卷理科第19 题就可以看出来,这两题均是证明倾斜角的关系,然后转化为斜率的关系,体现的还是设而不求的数学思想方法.

其实,以往高考题已经十分注重教材习题和阅读材料.由是2020年海南和山东新高考可见一斑.

例6(2020年新高考山东卷第5 题)某中学的学生积极参加体育锻炼,其中有96%的学生喜欢足球或游泳,60%的学生喜欢足球,82%的学生喜欢游泳,则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是( )

A.62% B.56% C.46% D.42%

对接教材 (人教A 版必修2,习题1.1 阅读材料: 集合中元素的个数)一般地,对任意两个有限集合A,B,有card(A ∪B)=card(A)+card(B)-card(A ∩B).

其实很多学生并不会做这道高考题,复习集合的时候,老师们也会忽略这个阅读材料,也就忽略了关于集合中元素个数的补充.

例7(2020年新高考山东卷第14 题)将数列{2n-1}与{3n-2}的公共项从小到大排列得到数列{an},则{an}的前n项和为____.

对接教材 (人教A 版必修5,习题2.3A 组6)

有两个等差数列2,6,10,...,190 及2,8,14,...,200,由这两个等差数列的公共项按从小到大的顺序组成一个新数列,求这个新数列的各项之和.

很多学生第一次接触新高考山东卷第14 题的时候,不理解什么叫“公共项”,也不知道两个等差数列的公共项从小到大排列可以组成一个新的等差数列,实际上复习的时候也会忽略这种灵活的题目,主攻求通项公式、求和、性质等.

三、高考复习策略方向

可以发现,新高考无论怎么创新,都是基于教材和新课程标准层层递进.这也就为我们日后的高考复习提供了几个方向:

1.立足于教材这基本点,深研新课标,发挥其引领作用

高考题近30%～45%的题目来源于课本中的典型例题、课后习题、复习参考题.八省适应性考试甚至出现了教材的阅读材料题、探究题.这引导我们复习要深挖教材,充分挖掘出教材中的典型例题的典型作用,加强对核心概念与核心数学思想的理解与掌握,达到增强知识理解,培养数学思维能力和熟练运用能力的目的.

2.抓好教研,聚焦课堂,突破关键能力的提升

数学知识的理解需要数学思维,在利用数学方法应用到具体问题中.要提高学生的数学能力,关键是提高学生的数学思维能力.需要深入研究学生的痛点,以学生问题为导向,分析学生知识和能力不足的地方.抓好课堂主阵地,注重知识的产生过程.课堂练习和课后习题注意渗透数学思维方法和通性通法.有意识的训练学生的阅读能力、思维能力和表达能力,这是学生的三大核心能力.

3.做好“不变”的,研究“可变”的,以不变应万变

教材及新课标是试题创新的来源,历届高考真题是高考备考的绝佳素材.注重基础题的考查,注重通性通法的提炼,淡化考试技巧.对于常考的问题常常讲、常常练,高频考点不回避中低难度的题.易错问题精讲精练,反复纠错,提高学生对易错题的辨识能力,避免一错再错.针对不同层次的学生,分段突破,分层要求.搜集整理教材的阅读题、材料题和探究题,不回避阅读材料题,以这些题目为依托,训练学生的阅读能力和思维能力等关键能力.

教材和新课程标准汇聚了无数专家的心血炼制而成,只有真正熟悉教材并且将其物尽其用,才能在高考改革的洪流中站稳脚跟,心中有度,无所畏惧.