新高考视域下高三数学微专题教学的实践与思考——以“同构式之指对互化”教学为例

广东省揭阳市揭阳第一中学(522000) 黄纯洁

随着《普通高中数学课程标准(2017年版)》的贯彻实施,我国基础教育正迈入更加注重培育核心素养的新时代!建立核心素养与课程教学的内在联系,充分挖掘数学学科教学在全面贯彻党的教育方针、落实立德树人根本任务的作用,使核心素养的培育融入课堂教学实际,是这一轮改革的重要任务.在能力立意而非知识立意统领的高考命题制度下,如何培养学生的数学核心素养就变得尤为重要.关于核心素养的讨论在当下是一个热点.高中数学要发展学生的数据分析、数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析六种核心素养; 要让学生学会用数学眼光观察世界,用数学思维分析世界,用数学语言描述世界.

高三数学复习课质量的高低直接影响学生对数学知识与方法的深入理解、思维能力的提升及良好数学素养的形成.近年来,微专题复习课正成为大家广泛认同的一种有效的课型,它是落实核心素养的重要载体.所谓“微专题”,是指立足于具体的学情、教情和考情,选择一些切入点小、角度新、针对性强的“微型”复习专题,力求解决复习中的真问题和实问题.利用同构化思想解决导数压轴问题是近年高考的一个热点,本文结合“同构式之指对互化”的教学实践谈谈对“微专题”复习的一些思考.

1 知识回顾,探究学习

1.1 设计同构式之指对互化的“先行组织者”

奥苏贝尔认为,在有意义的接受学习中,新的学习总是建立在原先的学习之上,人们总是利用原先的学习来促进后继的学习,而后继的学习又可以巩固和加深原先的学习.这里的原先学习是指学生已有的知识和经验.在学生的学习中,已有知识和经验是新的认识活动的必要基础,在引导学生从事新的学习活动中,教师应该十分注意和帮助学生获得必要的经验和预备知识,奥苏贝尔称这种必要的经验和预备知识为“先行组织者”.

微专题教学的本质就是“为迁移而教”,为培育数学核心素养而教.“为迁移而教”的实质是塑造学生良好的认知结构.因此,微专题教学要重视学生原有的认知基础,要从学生思维最近发展区出发设计问题,激活知识梳理,构建起解决某一类问题较为清晰的“路线图”,这样既顺应了学生原有的认知基础,又能逐步改变学生的认知图式,从而使学生在新情境的问题解决过程中形成结构化的、具有高度认知灵活性的图式.

在教学中,由于原有的认知结构同构式与指对互化存在着数学知识和逻辑知识上准备不足的困难,因此,在教学的开始,我从具体的实例出发,设计“先行组织者”,在学生的头脑中植入下述知识“生长点”.

问题1同构式是什么?

教师引导学生思考,然后在课件上呈现相关定义: 同构式源于指对跨阶问题,形如y= ex+x与y=x+lnx属于跨阶函数,y= ex+lnx属于跳阶函数;在解决指对跳阶函数问题时,如已知等式恒成立求参数取值范围或证明不等式,如果我们能构造跨阶函数的同构式,则会大大简化分析和计算,而找到这个函数模型的方法,就称为同构法.

问题2已知a ＞b ＞e,证明:alnb ＞blna.

证明原不等式可化为有相同的结构,令f(x)=则f′(x)=当x ＞e时,f′(x)＜0,f(x)单调递减,因为a,b ∈(e,+∞)且a ＞b,所以f(b)＞f(a),即

通过问题2 引导学生总结出同构化的步骤: 对不等式进行变形,化成左右两边具有相同结构的式子(即外函数相等),再通过单调性得出内函数关系从而解出不等式.体验如下的高考真题.

例1(2020年高考新课标I 卷理科第12 题)若2a+log2a=4b+2 log4b,则( )

A.a ＞2bB.a ＜2bC.a ＞b2D.a ＜b2

分析因为4b+2log4b=22b+log4b2=22b+log2b=22b+log22b-1,所以2a+log2a= 22b+log22b-1.设f(x)=2x+log2x,利用作差法结合f(x)的单调性即可得到答案.

解析因为4b+2log4b=22b+log4b2=22b+log2b=22b+ log22b -1,所以2a+ log2a= 22b+ log22b -1,故2a+log2a ＜22b+log22b.设f(x)=2x+log2x,则f(x)为增函数,所以f(a)＜f(2b),所以a ＜2b.

例2(2020年高考新课标II 卷理科第11 题)若2x-2y ＜3-x-3-y,则( ).

A.ln(y-x+1)＞0 B.ln(y-x+1)＜0

C.ln|x-y|＞0 D.ln|x-y|＜0

分析将已知2x-2y ＜3-x-3-y按照“左右形式相当,一边一个变量”的目的变形,然后逆用函数的单调性.

解析由2x-2y ＜3-x-3-y移项变形为2x-3-x ＜2y-3-y.设f(x)=2x-3-x易知f(x)是定义在R 上的增函数,故由2x-3-x ＜2y -3-y,可得x ＜y,由y-x ＞0,得到y-x+1＞1,从而ln(y-x+1)＞0,故选A.

1.2 构建知识网络

(1)三大基本初等函数

(3)四大常见的同构函数

(4)四大同构函数之间的相互转化

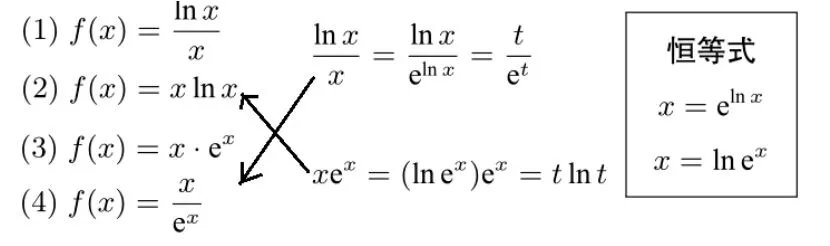
设计意图: 由旧知引出问题,既复习了旧知,又启发学生思考,引出本专题的学习.从自然语言、图形语言和符号语言三方面进行精加工编码,帮助学生建立四大同构函数良好的图式.

2 知识应用深度剖析

2.1 典型例题

设实数k ＞0,若对任意的x ∈(0,+∞),不等式≥0 恒成立,则k的取值范围是____.

解析ekx -≥0⇔kekx≥lnx ⇔kx ·ekx≥xlnx= elnx ·lnx.设f(x)=xex,则f(kx)≥f(lnx),所以kx≥lnx,所以k≥

2.2 变式训练

对于∀x ＞0,不等式ax≥loga x(a ＞0 且a ＞1)恒成立,则a的取值范围是____.

解析由ax≥loga x,有exlna≥xlna·exlna≥xlnx= elnxlnx,设f(x)=xex,则由于f(x)在(0,+∞)单调递增及f(xlna)＞f(lnx),推知xlna≥lnx,所以所以

2.3 高考链接

例3(2020年山东卷第21 题)已知函数f(x)=aex-1-lnx+lna.

(1)当a= e 时,求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积;

(2)若f(x)≥1,求a的取值范围.

解法1由aex-1+≥1,可得

所以lna≥0,所以a≥1.

解法2由f(x)=aex-1-lnx+ lna≥1,移项得:aex-1+lna≥⇔lnx+1,即elna+x-1+lna≥lnx+1,两边同时加(x-1)得elna+x-1+x+lna-1 ≥lnx+x,即elna+x-1+(x+lna-1)≥lnx+elnx.设g(x)=x+ex,则g′(x)=1+ex ＞0,所以g(x)单调递增,所以lna+x-1 ≥lnx,即x-lnx+lna-1 ≥0.设h(x)=x-lnx+lna-1,则h′(x)= 1-所以h(x)在(0,1)单调递减,在(1,+∞)单调递增,所以h(x)min=h(1)=lna-1 ≥0,所以a≥1.

设计意图: 通过典型例题和变式训练,巩固和提升学生对同构式的理解,以及利用指对互化解决恒成立求解参数范围问题,培养学生分析问题和解决问题的能力.

3 课后训练专题小结

3.1 强化训练

(1)已知xex≥axalnx对∀x ＞1 恒成立,则a的取值范围是____.

(2)函数f(x)=xex-x-lnx的最小值为____.

(3)设实数m ＞0,若对任意的x≥ e,若不等式恒成立,则m的最大值为____.

(4)已知关于x的不等式-x-alnx≥1 对任意x ∈(1,+∞)恒成立,则实数a的取值范围为____.

3.2 专题小结

解决导数中的指对跳阶问题方法步骤:

(1)利用同构思想,对原不等式进行同构变形;

(2)通过指对互化,找到相应的同构函数;

(3)利用同构函数的单调性和最值,解决恒成立求解参数范围问题.

设计意图: 感受数学的简洁美,对称美,统一美;体会同构化的思想;设计课后训练,以强化学习的知识,培养学生独立解决问题的能力,体会同构式之指对互化在解决导数压轴题中的重要作用.

4 教学思考

4.1 重基础,构建微专题复习的知识体系

高三数学微专题是以知识点为中心,同时具备专题性和综合性的特征,作为数学教师,应理清各个知识点之间的内在联系,进行相关内容的合理设计.微专题教学的本质就是“为迁移而教”,为培育数学核心素养而教.“为迁移而教”的实质是塑造学生良好的认知结构.因此,微专题教学要重视学生原有的认知基础,要从学生思维最近发展区出发设计问题,激活知识梳理,构建起解决某一类问题较为清晰的“路线图”.

4.2 重过程,促进深度学习与微专题复习的有机融合

核心素养是学生在学习过程中逐渐形成的正确价值观、必备品质和关键能力,是知识、能力、思维、方法、情感和价值观的有机统一,核心素养的培养和发展不是一蹴而就的,培养和发展学生的核心素养,一定要关注教学过程.高三数学微专题复习主要针对一轮复习效果的提高,关注对问题的深度学习和思考,从学生核心素养形成的视角出发,进行数学微专题的设计.

4.3 重反思,优化数学知识与思想方法的整合

有效运用微专题中设计的数学基本概念和基本原理进行解题,注重数学知识与思想方法的融合与统一,可以帮助学生构建数学知识与思想方法体系,进而提升他们解决问题的综合能力.微专题教学中要引导学生对认知结构中已有的一些解法进行反思和提炼,让学生认识到知识方法之间的联系,帮助学生建立起对一类问题的整体认知,进而生成处理一类问题的基本方法,这样才能做到举一反三,触类旁通.