运用求导法证明不等式

安徽省无为中学(238300) 朱小扣 鲁贤龙

不等式的证明一直是联赛常考的考点,其证明方法千变万化.往往让人毫无头绪,本文阐述了用求导的方法来证明一类不等式,希望能帮助大家.

一、求导法与琴生不等式结合

例1(数学通讯问题455)已知正实数a,b,c,求证:

证明考虑到待证不等式是齐次的,不妨设a+b+c=1,故只需证:

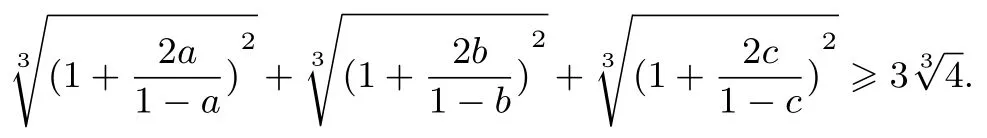
令f(x)=(0＜x ＜1),则:f′′(x)=恒成立.由琴生不等式得:即:故原不等式得证.

例2(数学通讯问题416)已知正数a,b满足a+b= 2,求证:≥a2+b2.

证明将待证不等式≥a2+b2两边同除以2ab得:

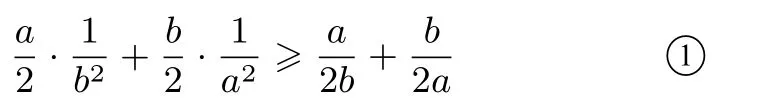
故只需证明①式成立即可.令f(x)=x2,则f′′(x)=2＞0,故由加权琴生不等式可得:

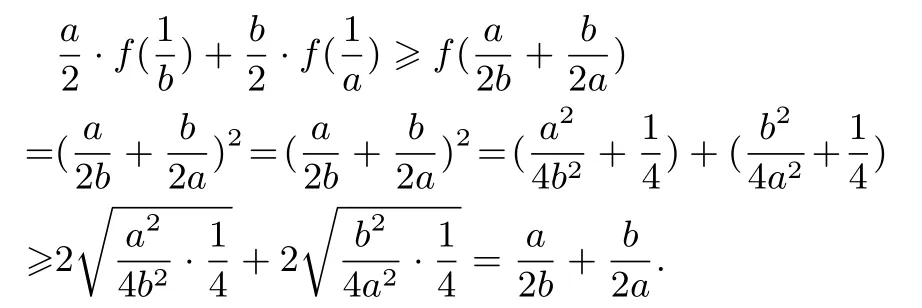
故①式成立,原不等式得证.

二、求导法与切线法结合

例3(数学通讯问题455)已知正实数a,b,c满足a+b+c=1，求证:

证明(权方和不等式)故只需证明:即要证:

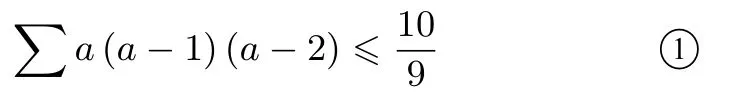
由切线法易知f(x)=x(x-1)(x-2)在处的切线方程是y=故只需证

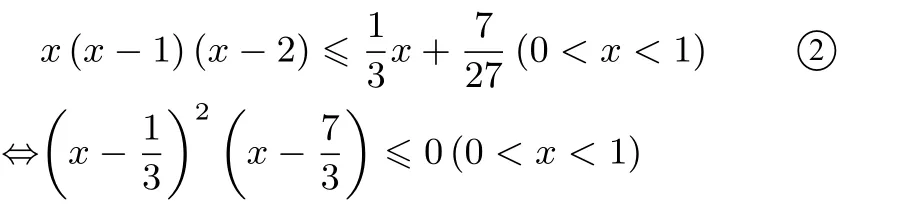
由②式得到:a(a-1)(a-2)≤b(b-1)(b-2)≤,c(c-1)(c-2)≤三式相加得: ∑a(a-1)(a-2)≤即①式成立,故原不等式得证.

例4(数学通讯问题332)已知正数x,y,z满足xy+yz+zx≤3,求证:

证明先证:

实际上,

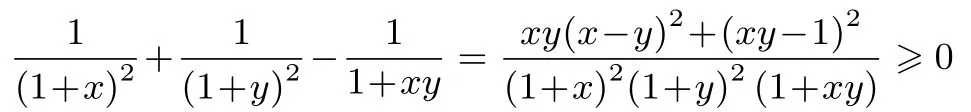
同理:

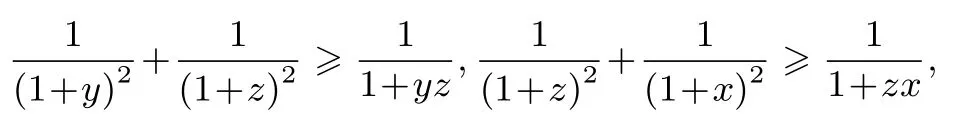
①与上两式作和得:

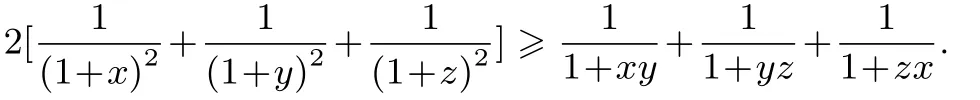
令a=xy,b=yz,c=zx,则问题转化为在:a+b+c≤3的条件下,求证:由切线法得只需证:

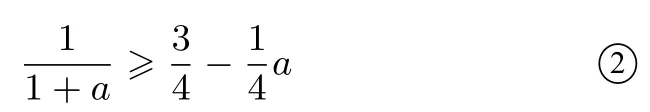
实际上4 ≥(1+a)(3-a)⇔(a-1)2≥0,故②成立.同理,②上两式作和得:故原命题得证.

利用求导求出切线法,可以推广到构造支撑函数解题,只要可以构造一元的局部不等式即可.

例5(2004年波兰奥林匹克)已知正数a,b,c且满足a2+b2+c2=1,求证:

证明尝试构造支撑函数:≥A · x2+B,由再由以下证明:

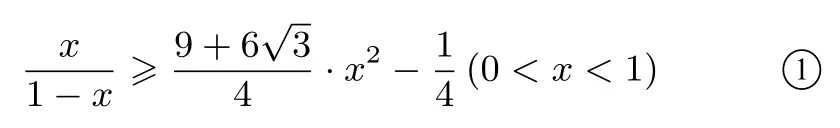
实际上,

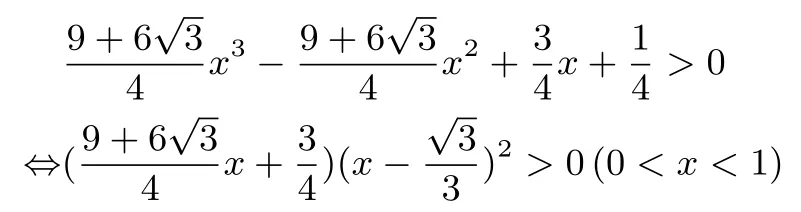
三、固定变量求导法

例5(数学通讯问题27)已知a,b,c ＞0 且a+b+c=3,求证: 2(a3+b3+c3)+3abc≥9.

证明不妨设a≥b≥c,先固定b,则c=3-a-b,c′a=-1.记f(a)=2(a3+b3+c3)+3abc,则

由a≥b≥c及a+b+c= 3 知b ＜2,故f′(a)=9(a-c)(2-b)≥0,故f(a)单增

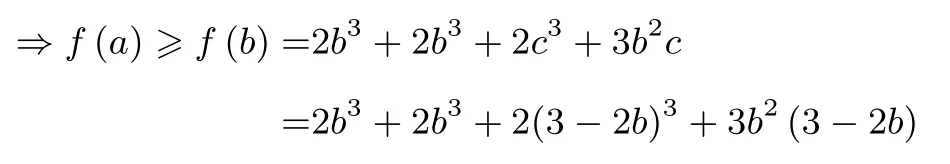
记h(b)=2b3+2b3+2(3-2b)3+3b2(3-2b),则

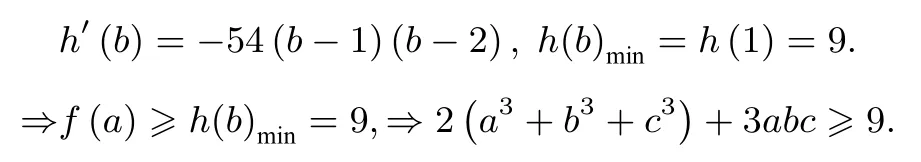
例6(第25 届IMO)已知x,y,z≥0 且x+y+z= 1,求证: 0 ≤xy+yz+zx-2xyz≤

证明先证:

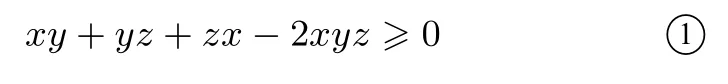
xy+yz+zx-2xyz≥xyz+yzx+zxy-2xyz=xyz≥0,故①式成立.再证:

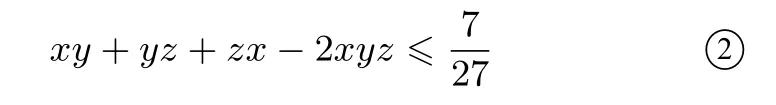
不妨设x≤y≤z,先固定y,则z= 1-x-y,z′x=-1.记f(x)=xy+yz+zx-2xyz,则f′(x)=y-y+z-x-2yz+2xy=(z-x)(1-2y).由x≤y≤z及x+y+z=1知y≤故f′(x)=(z-x)(1-2y)≥0,可知f(x)单增.故f(x)≤f(y)=y2+y(1-2y)+y(1-2y)-2y2(1-2y)=4y3-5y2+2y.

由x=y≤z及x+y+z= 1 知0 ≤y≤记h(y)= 4y3-5y2+ 2y,则h′(y)= 12y2-10y+ 2 =2(2y-1)(3y-1)≥0,h(y)max=f(x)≤h(y)max=当且仅当x=y=z=时取等号.故②式成立.综合①②可得原不等式成立.

如果有三个变量,可以先固定一个,再用求导法就可以了.

例7(数学通讯问题370)已知正数a,b,c满足a+b+c=3,求P=的最大值.

解不妨设a≥b≥c,a+b+c= 3.先固定住a,将c看成b的函数,则c=3-a-b,c′=-1,将P看成是b的函数: 令f(b)=则

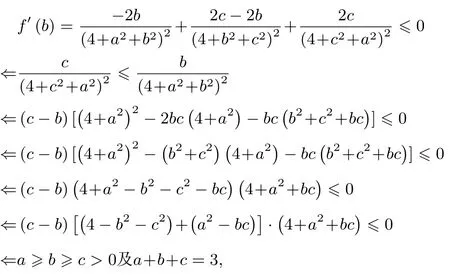
故

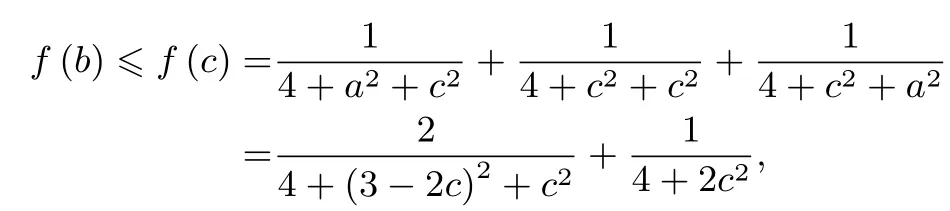
当a=b=c= 1 时,P=猜测Pmax=往证: 当0＜c≤1 时,

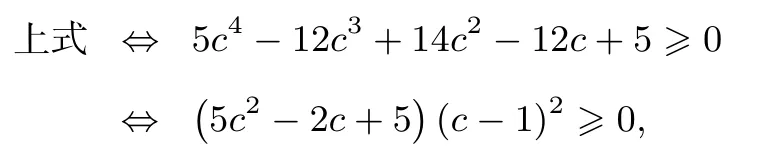
故Pmax=当且仅当a=b=c=1 时取等号.

四、全导数法

例8(数学通讯问题27)已知a,b,c ＞0 且a+b+c=3,求证: 2(a3+b3+c3)+3abc≥9.

证明齐次化后即证: 2(a3+b3+c3)+ 3abc≥记f(a,b,c)= 2(a3+b3+c3)+ 3abc -不妨设a≥b≥c,令t ∈[0,c],再令a1=a-c,b1=b-c.记

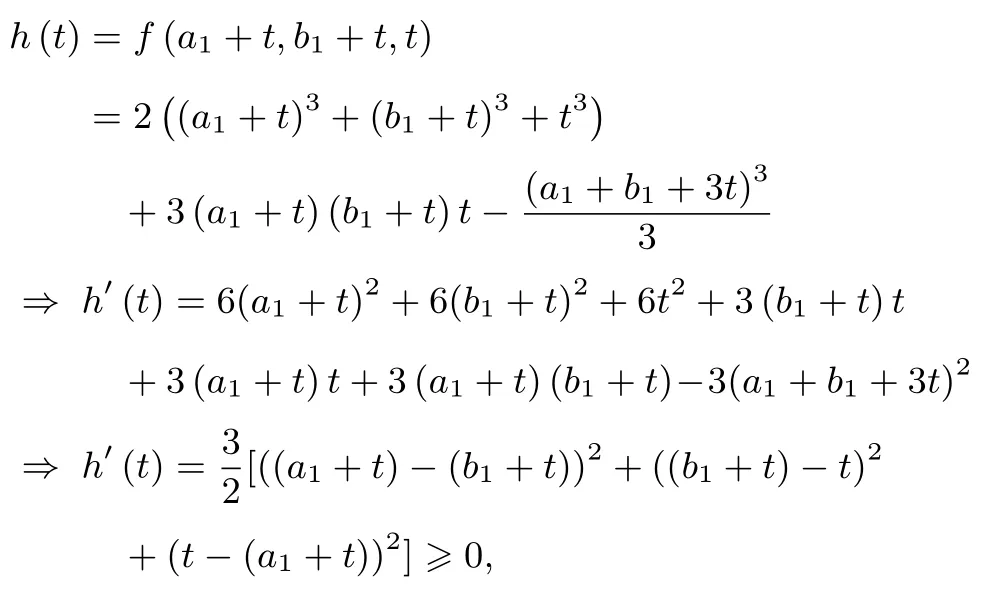
故h(t)在[0,c]上单调递增,从而

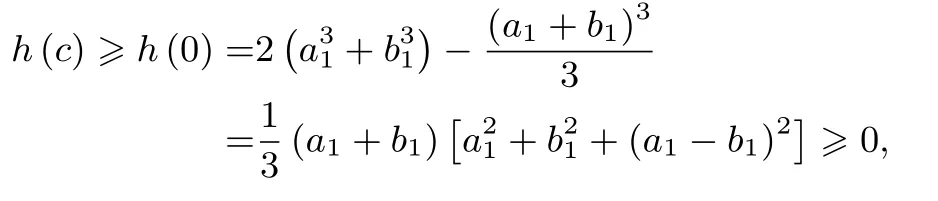
可得原不等式成立.

例9已知a,b,c ＞0,求证:a3+b3+c3+ 3abc≥ab(a+b)+bc(b+c)+ca(c+a).

证明记f(a,b,c)=a3+b3+c3+3abc-ab(a+b)-bc(b+c)-ca(c+a).不妨设a≥b≥0,令t ∈[0,c],再令a1=a-c,b1=b-c.记

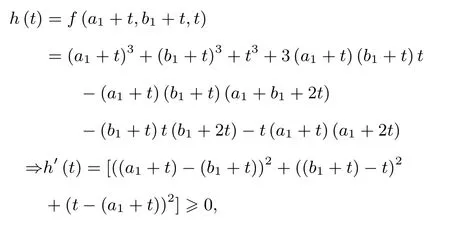
从而h(t)在[0,c]上单增,故有

可得原不等式成立.

不难得到上述两题h′(t)≥0 与f(a,b,c)对a,b,c偏导数之和大于零等价.如例8 中,

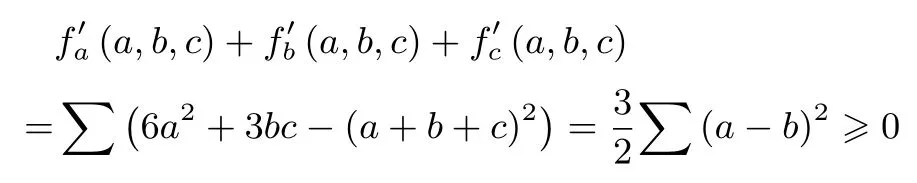
与h′(t)≥0 等价,出于写法的简洁,所以有时我们用偏导数之和——全导数[f(a,b,c)] =f′a(a,b,c)+f′b(a,b,c)+f′c(a,b,c)≥0 来代替h′(t)≥0.

五总结

上述介绍了四类求导法证明不等式的方法,实际上用导数证明不等式的方法还有很多,希望大家能继续延拓.