促进思维发展的数学课堂提问策略

林丽琴

（仙游县蜚山第二小学，福建 仙游 351200）

在小学课堂中，提问是一种重要的教学方法。面对问题，学生仔细思考、寻找资料、分析归纳、总结（回答问题），将相关内容纳入自身的知识体系。学生解决问题的过程，其实是一个思维发展的过程。通过启发式、递进式、开放式三种提问方式，促进学生思维活动从低级走向高级，最终实现学生在小学阶段从直观行动思维到经验型抽象思维的转变。［1］

一、启发式提问：深钻教材，抓准时机，引导认识事物本质特征

《义务教育数学课程标准（2011 年版）》明确要求：教师在教学的过程中，要懂得灵活使用教材。教师备课时，需充分利用教材编排特点，理解教材中每个模块和每个探究性结构之间的横纵联系，理清思路，划分重难点，真正吃透教材。在学生实践探索新知的过程中，抓准时机，采用启发式提问，具有针对性和有效性，有助于落实学生的主体地位和发挥教师的主导作用，逐步引导学生从具体形象思维向抽象型转变，以便更好地系统掌握所学的知识。［2］

例如，以人教版六年级上册《圆的认识》一课片段教学为例，通过对教材的解读和根据本班的实际情况，设计以下探索圆的特征的教学环节：动手实践—交流探究—归纳特征—再次画圆。

师：请同学们用圆规尝试画圆。边画边想，画圆时要注意哪些问题？

（师巡视指导）

师：大部分的同学都画好了，谁愿意告诉大家用圆规画圆时应注意什么？

生1：尖尖的那只脚不能动。（圆规要固定）

师追问：动了会怎样？（圆就跑了，画不了）

生2：两条腿的距离不能改变？

师追问：为什么？（也画不成圆）

师：同样用圆规画，为什么有的同学画的圆大，有的画的圆小呢？（师举着两个大小不同的圆）

生3：圆规两只脚的距离不一样。

师追问：圆规两只脚的距离不同，也就是什么不一样？（半径不同）

在师生问答的互动环节中，把握学生的学习状态，动手实践，交流归纳，培养学生善于思辨的习惯，学会概括整理。逐步从形成事物的表象到认识事物内在的本质特征，即从具体形象思维过渡到经验型抽象思维的发展，让学生感受到知识的魅力和应用知识的乐趣，从“要我学习”转变为“我要学习”。

二、递进式提问：分析学情，预设梯度，链接新旧知识体系

课前，教师了解学生对知识的真实掌握情况，是实现课堂有效提问的关键。只有充分了解学生的实际情况，因利是导、有的放矢、对症下药，所预设的问题才有明确的目的和针对性。教师合理预设难度各异的问题，有针对性地让不同层次的学生都能有所进步，真正做到以学促教。

例如，人教版三年级下册《小数的初步认识》备课片断：

磨课一：

师：首先出场的是青蛙，青蛙使劲一跳，谁能说说小青蛙跳了多远？

……

磨课二：

视频出示青蛙跳远的画面。

案例中，由于第一次备课时没有深入解读教材，预设的问题不严谨，学生的回答五花八门，有1 分米、10 厘米、一格、一段等答案，不利于学生严谨的逻辑思维的发展。

师：首先出场的是青蛙。青蛙使劲一跳，谁能说说小青蛙跳了几格？

生：一格。

师：请大家看画面，一格是多远呢？

生：1 分米。

师：一米是10 分米，1 分米如果用分数来表示，是多少呢？

生：十分之一米。

师：同学们，这个十分之一米，也可以用小数0.1米来表示。［2］

片断磨课二中的每一个问题，都立足于启发学生的思维及新旧知识的联系，为学习新知识构筑桥梁。把所要学的新知识放置在整个相关知识体系中，注重知识间的结构和联系，处理好知识中点与点之间、点与整体之间的关系，善于利用知识间“出生点”“成长点”与“延伸点”。让学生充分感受数学知识点之间相互衔接，体会部分数学知识点可从不同角度进行分析和理解。

三、开放式提问：迁移方法，融会贯通，发散多种解题思路

学生随着年龄的增长，课堂发言的积极主动性呈现逐渐下降趋势，原因是学生的戒备心理在作祟，害怕答错而丢面子。开放式的提问可以为学生提供广阔的自由发展空间，让学生多角度地考虑问题并放松心情投入课堂，能有效解决高年级不管发言的问题。教师要善于利用开放式提问发展学生的思维。

以人教版六年级下册《圆柱的体积》一课片段教学为例。

师：关于圆柱的体积，你有哪些想知道的问题？

1.大胆猜想：怎样求圆柱的体积？

猜想1：要求圆柱的体积，和什么有关？为什么？

猜想2：猜猜圆柱的体积计算公式是怎样的？根据是什么？

2.探究验证思路：

师：刚才同学们对圆柱体积的计算公式进行各种大胆猜想，那么怎样验证这些猜想？你们有自己独特的想法吗？先独立想一想，再在小组内分享自己的想法。

在整个教学活动中，先让学生大胆猜想圆柱的体积计算方法，然后引导学生利用知识的迁移，化新为旧的转化思想方法，为探索圆柱的体积公式提供经验和方法，再由“面”到“体”。［3］通过动手操作，学生发现把圆柱沿直径切成若干偶数等分，可以拼成近似长方体或正方体。观察圆柱体转化为长方体或正方体这一过程的前后变化对比，发现圆柱的形状发生变化，但体积不变（图1）。利用转化思想化新为旧，最后利用长方体体积的公式，推导圆柱体积公式V=sh 或V=πr2×h。

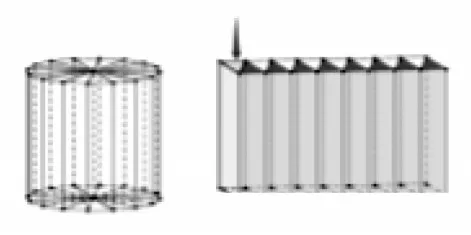
图1

有学生通过前面的操作，发现当长方体摆放的位置不同时，它们的底面和高发生变化（图2）。教师引导：想一想，如果不改变摆放位置，还能怎样求出圆柱体积？学生通过观察、讨论，发现这个长方体的底面与圆柱体侧面的关系，刚好是它的一半，高是圆柱底面半径，得出V=2πr÷2×r×h=πr2×h。

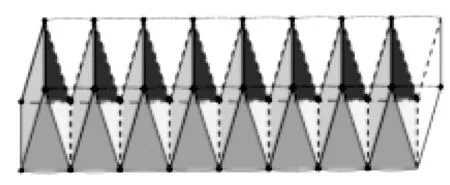
图2

通过以上两种不同的方法进行知识梳理，学生懂得融会贯通，避免方法单一片面、死记硬背公式的通病，积累数学活动经验，增强分析和解决问题的能力。

总之，在具体的教学过程中，教师需从学生的具体情况出发，根据实际情况，把握时机，选择三种形式的提问策略，逐步引导学生思维的发展。