量级估计在材料力学简化分析中的作用

李 敏 张雪松 李依伦 陈伟民

*(北京航空航天大学航空科学与工程学院， 北京 100191)

†(成都东软学院， 成都 611844)

**(巴黎- 萨克雷大学，土壤，结构与材料力学实验室，法国巴黎 91190)

††(中国科学院力学研究所，北京 100190)

本文中的量级估计泛指具有相同物理意义的物理量或无量纲量之间的比较，并不限定于数学上有严格约定的数量级定义与相关问题。

无论在科学研究还是工程设计领域，基于一定的假设进行问题简化是一种常见手段。作为机械大类的专业基础课，材料力学的分析方法充分体现了这一特征，其中学生最为熟悉的包括材料连续、均匀、各向同性假设，以及三种基本变形模式中的平面假设。

事实上，绝大多数假设条件只是最终给出的结果，其依据往往是各相关物理量包括无量纲量的比较：如果某些量相比其他量非常小，这些量或者其造成的影响将被忽略，这是假设简化的立足点。当然也有一些假设本身就是事实，只不过不是根据理论分析而是由实验现象得出的猜测，例如上面提及的平面假设更大程度上是为了避免引入复杂的数学推导，即便如此，在基本解适用范围讨论中往往也是基于物理量的量级估计。

在材料力学的问题分析中存在大量的量级估计，但是教材中通常只是给出了结论，没有细节论述，作为教师需要了解相关细节以便辅导学生，或者将其作为研讨课的素材。

本文内容来源于教学实践中对理论公式适用范围描述的细节，其中大部分归结于材料力学研究对象三维尺寸的差异或基于小变形条件，注意到这一点对于材料力学教师把握引导方向有一定的参考价值。

1 基本变形模式之间变形的量级估计

拉压、扭转与弯曲是绝大部分材料力学教材提及的三种基本变形模式[1-4]，其变形分别为

式(1)～式(3) 分别为一端固定一端自由均匀截面(常见为矩形与圆形，扭转为圆与圆环截面) 直杆承受轴向载荷F、轴向力矩T与横向载荷F的自由端轴向位移Δl(拉压变形)、扭转角φ(扭转变形)与挠度w(弯曲变形)，其中杆件长、宽、高分别为l，b，h(圆形半径为r)，E与G分别为材料弹性模量与剪切模量，A，IP与I分别为杆件截面面积、极惯性矩与(轴) 惯性矩。

式(1)～式(3)中拉压与弯曲变形的量纲同为长度，而扭转变形为无量纲的角度，所以首先基于物理意义比较拉压与弯曲变形的量级。在结构与载荷大小相同的情况下

式中kS与kB分别为杆件拉伸与弯曲刚度。很明显，对于常见的工程长梁，拉压变形比弯曲变形至少低2～3 个量级，或者换言之，拉压刚度比弯曲刚度至少大2～3 个量级。

认识到这个量级差异不仅对于后续能量原理中各部分取舍的讲解有益，更重要的是对于学生理解结构设计中梁杆尺寸匹配，特别是传感器细节设计有帮助。图1 是目前处于研究热点的柔性电子器件典型结构细节：为了获得拉伸方向(x方向) 较大的柔度，弯曲微梁是主承力结构的周期单胞。图2 是加速度传感器的微机械梳状结构：利用垂直于测量方向(x方向) 的微梁(AA与BB) 较大的变形，明显改变器件的电容用于表征x方向的加速度。

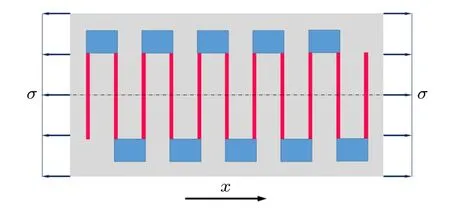
图1 柔性器件微梁结构示意图

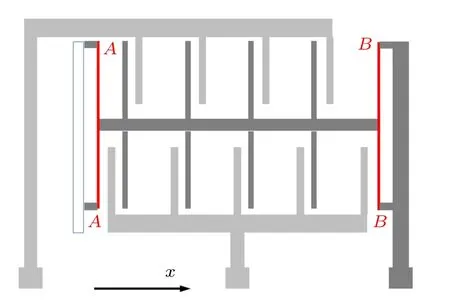
图2 加速度传感器梳状结构微梁示意图

除此之外还有大量力传感器、压力传感器、温度传感器都是利用微梁结构放大测量灵敏度，这种利用梁长度的方次效应提高灵敏度的模式与利用镜面偏转光路放大位移的模式类似，甚至可以联合使用–– 在微纳米材料性能测试领域，纳米压痕仪(包括原子力显微镜)利用了微梁变形+激光光路偏转，极大提高了位移(变形) 测量的灵敏度，目前医学界的大量检测设备也都使用了该方式。该领域类似的结构形式非常多，教师可以查找相关图片作为教学讲解实例。

其次，圆轴扭转导致的最大线位移与横截面半径r相关，与挠度w相比较不失一般性，考虑一对作用在端面上的F形成扭力矩，即T=2Fr的情况下

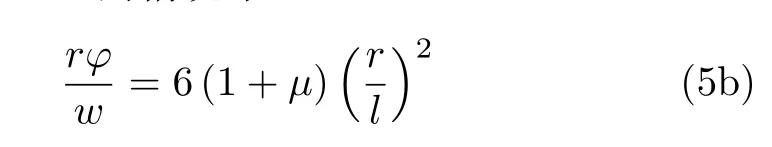
由此可见，一般情况下，扭转造成的最大线位移相比弯曲挠度也有2 个量级的差异，与拉压变形量基本相当。

这里考虑一种特殊情况–– 开口薄壁杆件的扭转：材料力学教材中对开口薄壁杆件扭转强调开口薄壁结构相比闭口薄壁结构，前者应力大，变形更大。切应力大的原因往往使用图3 加以说明[1]：在相同扭矩条件下，开口薄壁形成微扭矩的臂长δi相比闭口的臂长hi小很多，所以开口薄壁扭转切应力远大于闭口薄壁扭转切应力。事实上也可以观察图3看出开口薄壁变形大的原因：在开口薄壁扭转杆件的横截面上，完全类比于弯曲变形，包括应力分布模式，差异在于边界约束条件。开口薄壁变形的扭转角公式

图3 开口薄壁扭转变形横截面切应力分布示意图

其中˜h，˜δ分别表示与hi，δi同量级量。式(7) 表明两种位移基本相当，具体取决于杆件长度、横截面尺寸与壁厚之间的相互关系，由此可见薄壁结构开口将造成较大变形，极大降低扭转刚度。

2 基本变形模式中变形量的量级估计

除了不同变形模式之间的比较，同一种变形模式中也存在不同方向或者类型的位移(变形) 量，例如在弯曲变形模式中使用挠曲轴为唯一参量表征弯曲变形，其简化基础中包含忽略原始轴线方向的位移Δ，对于悬臂梁自由端承受集中力的情况，由挠曲轴总长与其水平轴投影之差[5]

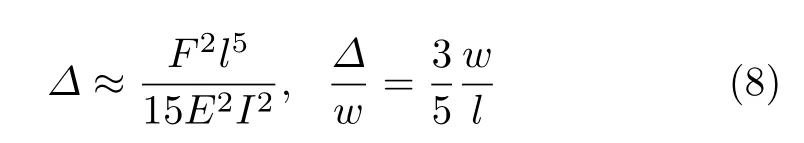
由此可见，在小变形条件下，自由端截面形心的水平位移相比轴线挠度属于高阶小量。

事实上，在弯曲应力章节中最为关键的公式适用范围推广是：弯曲正应力公式由纯弯曲扩展到横力弯曲，其基础是忽略了剪切效应对轴向应变的影响。关于该部分分为两种情况。

(1) 如果分布载荷q= 0 (如图4(a))，则不同截面翘曲程度一致(aa′=bb′)，截面翘曲并不显著影响轴向正应变及其相互关系，所以由纯弯条件导出的正应力公式可以推广到横力弯曲；

(2) 如果分布载荷q/= 0 (如图4(b))，则不同截面翘曲程度不同(aa′/=bb′)，剪切效应影响轴向应变，所以由纯弯条件导出的正应力公式推广到横力弯曲不正确，但对于长度大于高度5 倍以上的工程长梁，该公式仍然满足工程计算精度。

图4 横力弯曲截面翘曲影响示意图

对于第二种情况，教材中均未给出证明或原理性说明，利用三维弹性理论[6-7]或者有限元数值分析进行解释一定可行，但是从材料力学教学的角度，使用量级估计对于学生理解与掌握更加合适。为了不引入过于复杂的表达式，并考虑到讲解弯曲应力部分还未涉及广义胡克定律，所以此处不涉及由于横向挤压应力造成的轴向应变(事实上，挤压应力最大值为分布载荷q，其与轴向正应力有较大差异，由此引入的偏差也是小量)，仅仅考虑剪切效应的影响。

以中性轴处的切应变估计剪切效应的影响(图4(b) 中SS线)

其中εqx与εMx分别表示剪切与弯曲引入的轴向正应变，式(10) 中弯矩M采用ql2进行量级估计，其比值展示了二者有两个量级的差异，同时也为讲解长高比为5 的判据提供依据。

剪切效应不仅影响正应力分布，也影响弯曲变形(挠度)，关于该部分的描述在经典教材中都有体现[1]，其量级比同样等于高长比的平方，这里不再赘述。

3 变形协调分析中的量级估计

在平面应变状态应变分析部分[1]，图5(a) 表征仅存在切应变γ(εx=εy= 0) 时，α方位应变与γ的变形协调关系。与另外仅存在εx/= 0 或εy/= 0的状态不同，此变形协调图为了便于在原始几何构型上表征变形量，对变形状态进行了简化：仅γ/=0状态下，原始矩形OABC应该变形为OAB′′C′′(如图5(b))，而不是OAB′C′。笔者所教班级每年都有不少学生对此提出疑义，为了解决学生疑惑，除展示采用OAB′′C′′产生的不方便外，对由此带来的偏差进行量级估计是有益的。

观察图5(a)中与应变分析相关各量，主要是γdy以及与之同量级值，而采用OAB′′C′′模式造成偏差的量级为Δdy=(1-cosγ)dy(见图5(b))

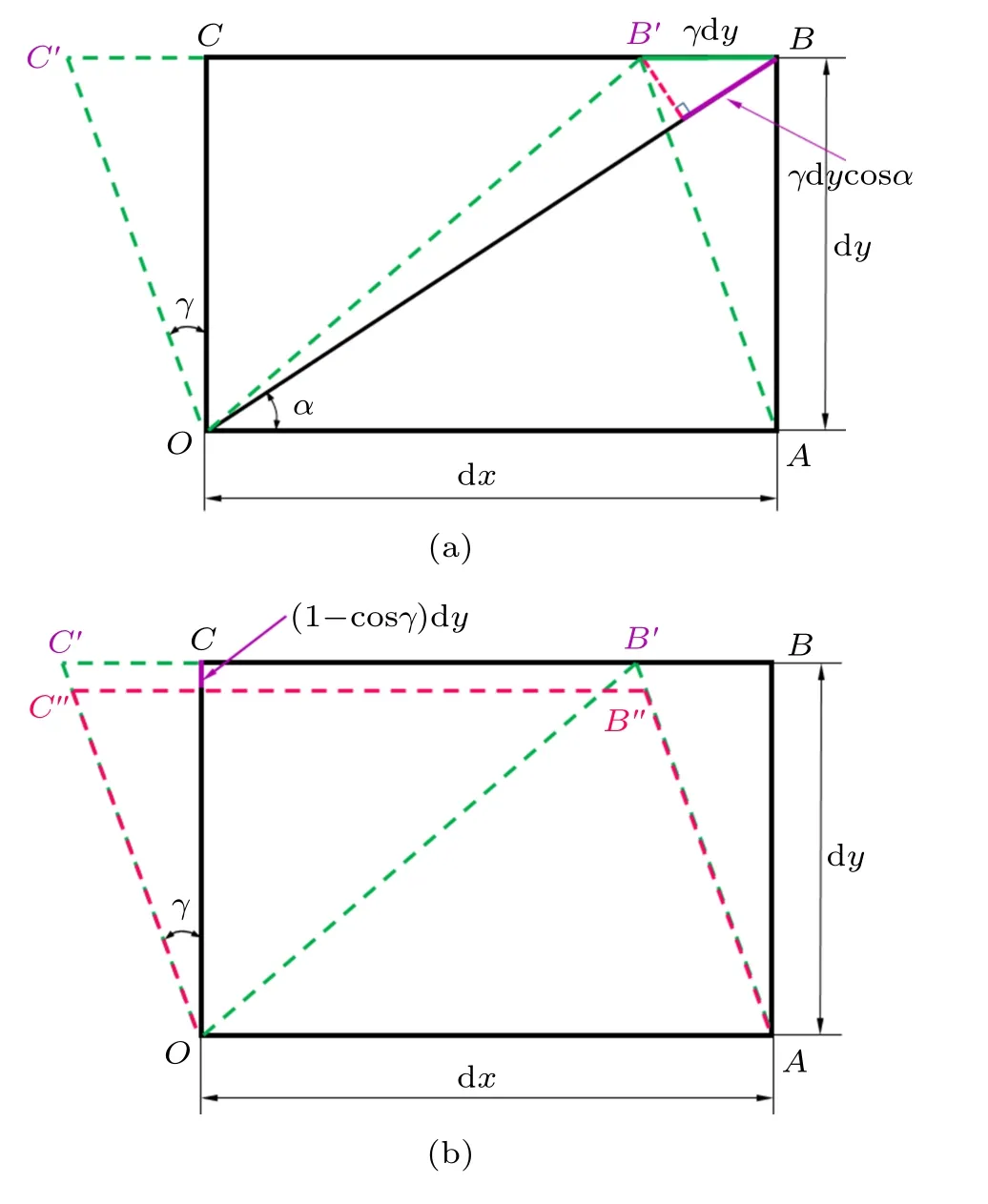
图5 平面应变状态纯剪变形协调示意图

在小变形条件下γ ＜＜1，由此可知，这种简化对变形协调中各量造成的偏差属于高阶小量，不影响后续结论的正确性。

类似的情况在变形协调分析中还有不少，包括学生们最熟悉的切线代圆弧，尽管材料力学中切线代圆弧方法被广泛使用，但并无推导式证明，只有部分章节中例题或习题的数值结果可以验证结论。事实上，使用量级估计的方式更为简洁，也便于学生理解，以该方法最早出现的桁架节点位移分析为例(见图6)

采用切线代圆弧方法，图6 中A点水平位移为AA2(AC杆的变形量)，如果按照圆弧相交的方法A点水平位移为AA3，二者差异为A2A3，使用量级估计的模式

图6 桁架节点位移分析变形协调示意图

在小变形条件下β ＜＜1，由此可见切线代圆弧方法对节点位移求解造成的影响可忽略，垂直方向影响类似，此处不再赘述。

4 小结

基于一定的假设进行问题简化是一种常见分析方法，提出假设并简化问题分析难度的基础在很大程度上是量级估计，即评估不同因素对问题影响的程度。

本文挑选了部分在材料力学教学过程中可以使用量级估计说明简化假设的实例，多与变形量相对大小有关，最终的结论往往归结于杆件不同方向尺寸的差异和小变形条件下变形量的大小，从而以另一个角度审视材料力学以杆件作为研究对象的目的：正是基于不同方向几何尺寸的差异，应力与变形的分析过程得到了极大简化，使材料力学分析方法有别于弹性力学，成为相对独立的模式。

量级估计不仅仅用于理论分析，该方式在解决实际工程问题中更为重要：事实上，工程实践中最能体现科技人员素质之处在于出现了非常规的状况，例如现有的分析软件或实验设备不具备完全对应的功能，此时需要科技人员基于量级估计的方法衡量影响因素的大小进行问题转化，充分利用现有手段解决非常规问题，这也是培养学生解决复杂系统工程问题能力的重要方面。