Matlab 求解理论力学问题系列(五)不同坐标系间的数据转换问题

高云峰

(清华大学航天航空学院， 北京 100084)

本系列文章介绍了很多利用数值计算处理问题的方法和过程。由于存在计算误差，以及人为的输入错误，计算得到的大量数据可能有误。作为Matlab求解理论力学的系列文章，十分强调计算的可靠性，所以前面曾经介绍过利用系统的守恒量来验证数值计算的精度，或者利用解析解进行对比测试。如果系统不存在守恒量，可以考虑退化等特殊情况(这时往往有解析解或守恒量)，对退化情况检验之后，再进行后续的计算。

某些问题可能在不同的坐标系中处理更方便，那如何判断其是否正确？本文介绍一种数据转换的方法，可以把不同坐标系的结果转换到希望的坐标系中来观察，并验证其准确性。

为此本文设计了这样两个问题：(1)在非惯性系中看，随手抛出的一个物体，其轨迹很复杂，我们如何来判断计算是正确的呢？(2)在地球某点观察太阳，太阳的视运动轨迹是什么曲线？

1 不同坐标系中的数据转换关系

设有矢量ρ和两个坐标系Oxiyizi和Oxjyjzj(图1)，基矢量分别为ei≜(exi eyi ezi)T和ej≜(exj eyj ezj)T。若用(ρ)i表示ρ在坐标系Oxiyizi中的分量，有

图1 矢量和坐标系

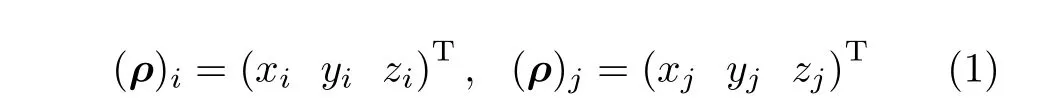
利用基矢量，矢量ρ可以表示为

矢量与坐标系没有关系，但是它在不同坐标系中的分量就与坐标系有关系了。因此一个问题就是：(ρ)i与(ρ)j有什么关系？

将式(2) 改写，有

由于两个单位矢量的点积等于其夹角的余弦，所以Aij也称为方向余弦矩阵，从而有[1]

从式(5) 类似有(ρ)i=Aik(ρ)k，从而得到坐标系转换矩阵的传递关系

以式(5)和式(6)为基础可以得到更一般的关系。假设Ox1y1z1是基准参考坐标系(如动力学中的惯性系)，ox′y′z′是平动坐标系(坐标系始终与基准坐标系平行)，ox2y2z2是任意的动系(如动力学中的非惯性系)，ox2y2z2初始时刻与ox′y′z′重合，转动后用三个角度(如欧拉角ψ，θ，φ) 来表示；P是动点，在基准坐标系中矢径为R，相对运动的矢径为ρ，动系原点的矢径为RO(图2)。

图2 空间一般坐标系

根据运动学关系，始终有[2]

式(7) 可以在任意坐标系中表示，根据式(5)，则有

式(7) 给出了一般情况下坐标转换关系，其中坐标转换矩阵还是比较复杂的，如果用欧拉角表示，利用式(6) 的关系后，有

2 不同坐标系中的抛物问题

两位观察者，A在地面上(惯性坐标系)，B在匀速转动的转盘边缘(非惯性系)。B随手抛出一物体，求两位观察者看到的物体运动轨迹(图3，不考虑空气阻力)。

图3 抛物示意图

图 4 是运动学关系示意图， 假设 (R)1=(a b c)T，转盘半径为r，转角为φ=ωt，B的位置在动系中为(r)2=(0r0)T，出手初速度在动系中为(v)2=(vx0vy0vz0)T。

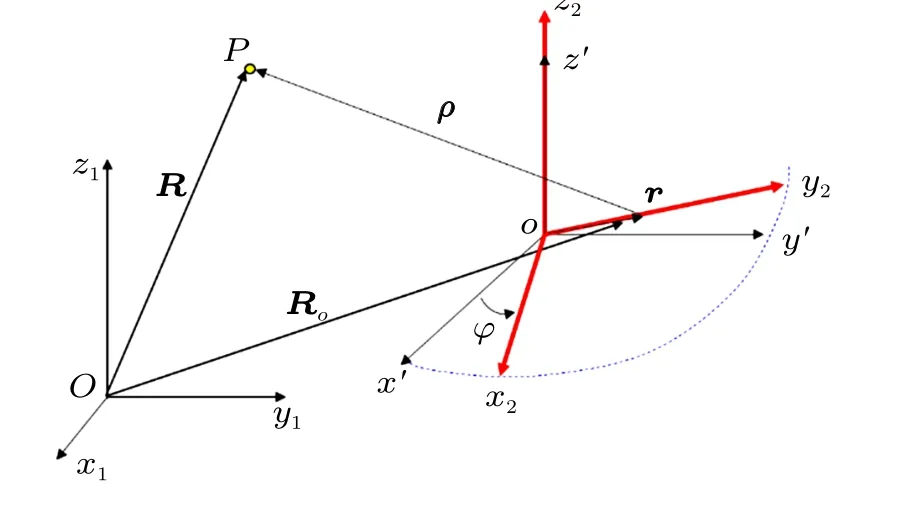
图4 运动学关系

注意物体在不同坐标系中运动的动力学方程是不同的，根据理论力学知识，在非惯性系中动力学方程为

展开后的方程及初始条件为

给予具体参数

可以计算出结果，如图5 (空间三视图) 和图6 (xy平面俯视图)。

图5 曲线的空间视图

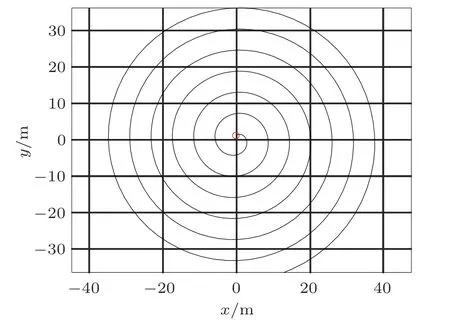
图6 曲线的俯视图

看起来曲线很复杂，我们怎么判断计算结果可靠呢？

众所周知，在惯性系中抛出一个物体其轨迹是抛物线，这是很明确的结论。因此可以这样处理：设惯性系中算出曲线为κ1，非惯性系中算出的曲线为κ2，把惯性系中的曲线κ1数据转换到非惯性系中得到曲线κ3，如果κ3能与κ2完全重合(两者误差小于给定的误差，如积分的允许误差)，就认为非惯性系中的结果是可靠的。

从惯性系的角度看，动力学方程有

展开后的动力学方程及初始条件为

积分后结果如图7 和图8。我们有理由认为这些结果是合理可靠的，如曲线看起来是抛物线，俯视图是一根直线，表示抛物线在一个平面内。当然还可以利用运动过程中的机械能守恒来判断(略)，总之我们认为惯性系中这些曲线合理可靠。

图7 曲线的空间视图

图8 曲线的俯视图

现在的问题是如何利用惯性系的结果去证明非惯性系的结果正确？

式(7) 和式(8) 给出了不同坐标系之间数据的转换关系。具体到本问题中，转换矩阵很简单，z轴是平行的，退化为

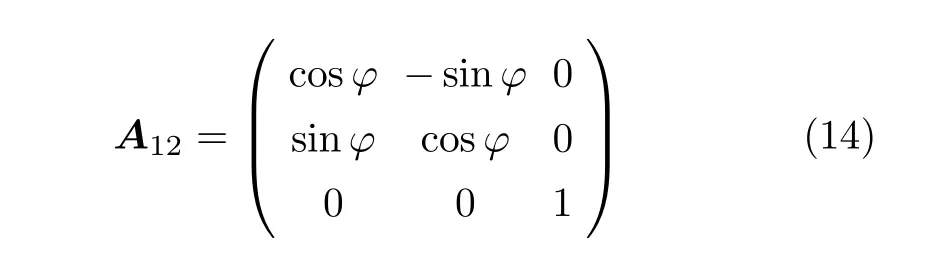
如果想把惯性系的结果转换到非惯性系，式(7)具体为

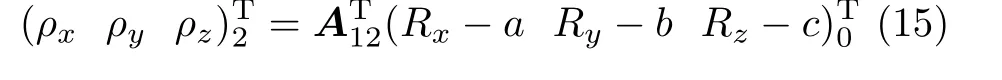
在Matlab 中，数据转换的源代码如图9 所示。

图9 数据转换的源代码

其中 (x1(i)y1(i)z1(i))T表示惯性系中第i个点，(x3(i)y3(i)z3(i))T是转换后得到的非惯性系中第i个点。在Matlab 中，A12’ 表示对A12 进行转置。

数据转换后，可以看到每个圆圈(非惯性系中直接算出的结果)都包含一个圆点(从惯性系中转换得到的结果)，说明两者的精度都很高(如图10 和图11所示)。当然在比较的时候要注意，不同坐标系中的积分要同步，用等步长积分正好可以实现这一点。

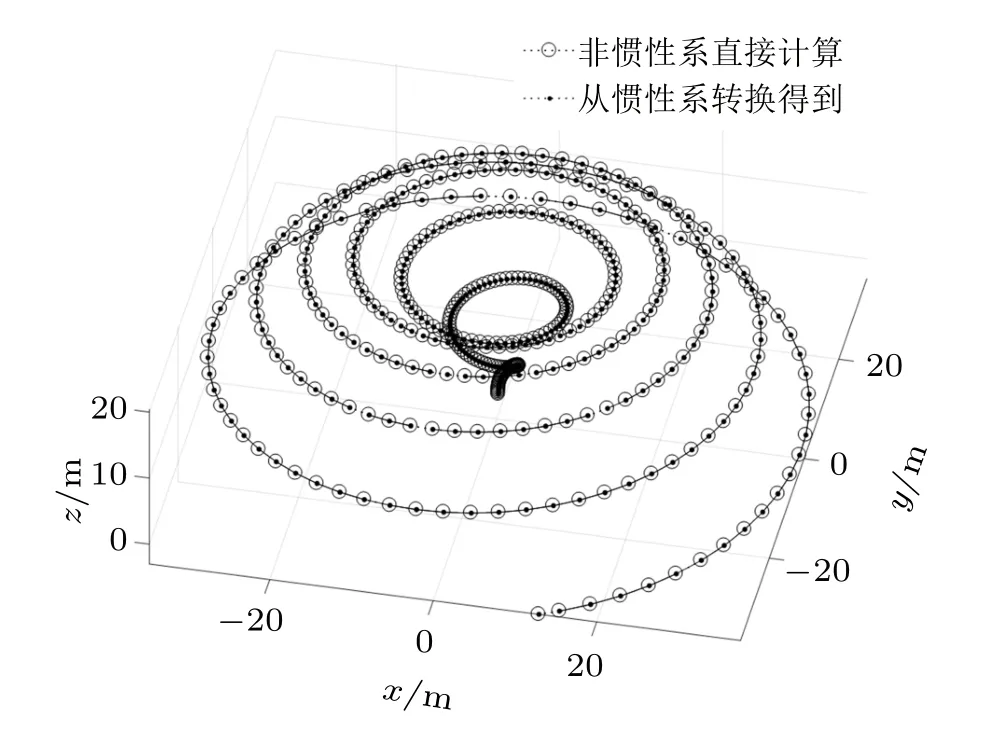
图10 非惯性系中的空间图

如果想把非惯性系的结果转换到惯性系，结论依然很可靠(具体略)。综合起来，说明图5 和图6的结果虽然有点出乎意料，却是正确的。

根据这一事实，未来处理非惯性系的动力学问题时，除了直接处理非惯性系中的问题(动力学方程复杂，结果也复杂) 之外，还多了一种选择：先在惯性系中进行分析(动力学方程简单，结论正确性容易验证)，然后再利用坐标系之间的转换关系，得到非惯性系中相应的结果。

3 太阳的视运动问题

人人都知道地球绕太阳的运动很简单，但是如果做个调查，你在当地看到的太阳运动轨迹(视运动轨迹) 是什么曲线？有什么特点？估计绝大部分人一时答不上来。而利用数据转换关系可以得出既简单又出乎意料的结论。

假设地球绕太阳为圆周运动，为简单设365 天。在日心坐标系OXY Z中，地轴(z轴) 的单位矢量为(0，-sinθ，cosθ)T，θ=23.5°(图12)。设时间为春分点之后第t小时，地球球心运动至

其中AU 为天文单位。设跟随地心运动的地心坐标系为oxyz，则转换矩阵为

下标S 表示太阳坐标系，E 表示地球坐标系。

在地球表面P点，建立当地的东北天坐标系PENZ(图12)。在地心坐标系中，P点的表达式为其中Re为地球半径，φ为当地纬度，β=2πt/24 为地球自转角度。

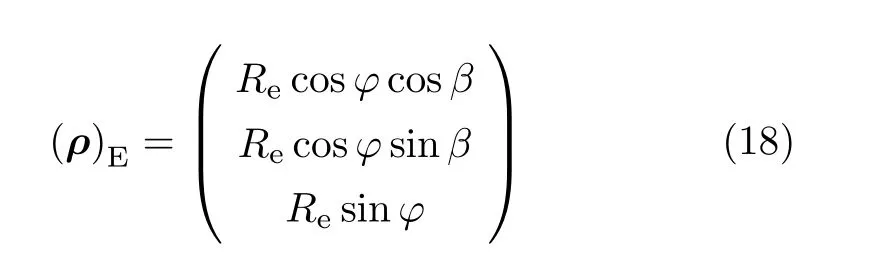
东北天坐标系相对地心坐标系的转换矩阵为

下标G 表示地理坐标系。

综合图12 和图13，仍有运动学关系R=Ro+ρ，在地理坐标系中分解为

图12 地球相对太阳的运动

图13 当地东北天坐标系

根据式(6)、式(17) 和式(19)，有

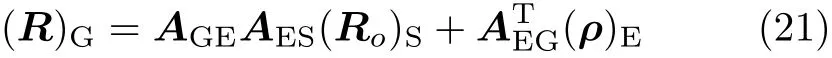
我们看到的太阳视运动， 就是式 (21) 中的-(R)G。式(21) 右边每项都为已知函数，代入数据后太阳视运动轨迹见图14，显示了全年特殊日期的太阳视运动轨迹：夏至当天轨迹偏北方，冬至当天轨迹偏南方，其他时间视运动轨迹会在夏至和冬至轨迹之间缓慢地变化，春分当天轨迹居中间。我们看不到水平面下方的太阳视运动轨迹，但仍画出。注意每一天的视运动轨迹并不封闭，因此全年的太阳视运动轨迹则很像一个弹簧，但是这个弹簧两端半径微小，中间半径略大，不过差距没有图中弹簧那么明显(图15)，另外视运动轨迹很密集，在夏至与冬至之间有365 圈。

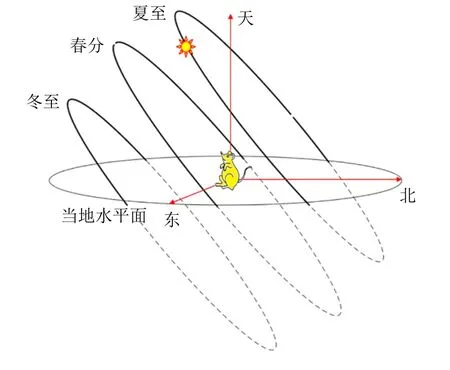
图14 太阳某一天的视运动

图15 全年太阳视运动示意图

4 小结

本文介绍了不同坐标系之间数据转换的一般方法，利用这一方法，可以把问题先在某个坐标系中处理好，然后再转换到另一个坐标系中。

在非惯性系抛体问题中，直接处理的方程比较复杂，结果也很复杂，难以判断其正确性。但是在惯性系中，动力学方程很简单，结果的物理含义也很清楚。利用不同坐标系之间的数据转换关系，可以很容易证明两种动力学方程的计算结果是正确的。

而在太阳视运动的问题中，从惯性系看地球的运动很简单，但在地球上看太阳的运动，则比较复杂，出乎很多人的意料。利用数据转换关系，可以把几个简单的运动(地球绕太阳的运动是圆周运动、地球上某点相对地球的运动也很简单) 直接转换为需要的结果。