伯努利方程教学设计中的若干问题1)

2021-12-31易文彬孟庆昌张志宏顾建农

力学与实践 2021年6期

易文彬孟庆昌邓辉王冲张志宏顾建农

(海军工程大学基础部，武汉 430033)

伯努利方程是流体力学课程教学中的重要内容。在教学设计中常包含实验演示、方程推导、物理意义讨论、相关知识点的联系拓展等环节。然而在教学实施的过程中，常常出现以下几方面问题，如演示实验解释不合理，学生对方程推导及方程中压强项的物理意义理解感到困惑，对方程的理解过于片面，不能建立知识点线面的联系。针对以上问题，本文梳理伯努利方程演示实验中的常见误解，分析伯努利方程不同的推导方法，讨论方程中压强项的物理意义，并将伯努利方程进一步联系拓展，以加深学生对内容的理解认识，建立科学严谨的分析方法。

1 演示实验中的若干误解

在课程内容引入时，教师往往通过一些简易的演示实验来激发学生兴趣，然而对演示实验的解释往往一笔带过，甚至忽略了方程使用的限制条件，给出错误的解释，反而不利于学生科学严谨地分析问题。

吹纸片实验是早期课本常用的一个演示实验(图1)。捏住纸片的一端，用嘴或者吹风机对着纸片的上方吹气时，纸片则向上抬起。由于观察到纸片上方的气流速度快，压强低，学生很容易误认为是伯努利方程的原因。事实上，纸片上方和下方的流体并不处于同一流线，且初始时二者机械能也不相等(上方吹出气流的机械能大于下方气流的机械能)，不满足伯努利方程的适用条件[1]。

图1 吹纸片实验

由实验测量可知射流的压强与周围环境压强基本相等，吹出的气流压强和周围大气压差别不大。吹纸片实验中纸片之所以向上抬起主要与流体黏性导致的康恩达效应以及纸片初始弯曲弧度有关[2-3]。流体流过弯曲的壁面时，因为黏性的作用，射流带走周围的流体向下游流动，导致附近压强降低从而射流向壁面偏转。根据力作用的相互性，壁面也受到指向射流方向的力，因此纸片会向射流方向抬起。射流沿着平直的壁面流动时，康恩达效应不明显。如果纸条自然下垂，并没有形成弧度，此时向下吹气，则纸片摆动幅度较小，且不会出现方向性。

图2 所示的气顶球实验是一个较为有趣的演示实验：实验时吹风机向上吹气保持小球悬浮于吹风机上方，当水平移动吹风机时，小球也会随之水平移动，甚至吹风机倾斜一定的角度，上方悬浮的小球也随之移动而并不落下。文献[4-5] 对该实验进行了讨论，但是关于气顶球实验的解释争议较大。

图2 气顶球实验

为了解释气顶球实验现象，本文基于CFD 软件进行了数值模拟。计算中的小球为标准的乒乓球，直径为0.04 m，重量为2.7 g，距离下方射流出口0.3 m。计算可得射流出流速度为12.7 m/s 时，小球可保持平衡。图3 为射流正对球心时的流场的速度分布。观察小球下方射流速度分布：由于黏性的作用，射流带动周围静止的空气，同时射流核心区变细。图4 为射流正对球心时流场的压强分布，虽然射流和周围空气流速差别较大，但是压强差别较小。

图3 射流正对球心时流场的速度分布

图4 射流正对球心时流场的压强分布

图5 为射流正对小球左侧时的速度分布，图6为小球表面的压强分布。小球左下方为驻点，受射流的冲击作用为高压区；小球左侧流速较大，由流线伯努利方程可知，此处为低压区。计算得到小球受到水平方向的合力向左，为5.5 mN，相当于0.2 倍小球的重量，此力拉动小球向左移动。其中一种解释为康恩达效应导致小球左侧压强降低，进而产生水平的作用力，同时压强降低会出现流线弯曲且流动加速的现象[6]。

图5 射流正对小球左侧时流场的速度分布

图6 射流正对小球左侧时小球的压强分布

2 伯努利方程的推导及物理意义

不同流体力学教材中关于伯努利方程的推导有不同的方法。有的是基于理想流体运动微分方程(欧拉方程或兰姆方程)沿流线积分得到，有的是基于功能原理推导。不同的推导过程难易不同，学习了解多种推导方法有助于学生加深对伯努利方程的认识理解。

2.1 推导方法一

在定常流场中，基于牛顿第二定律分析理想流体微元体的受力，可得到欧拉运动微分方程为

式中，p为流体的压强；ux，uy，uz分别为速度u沿坐标轴x，y，z三个方向上的分量；fx，fy，fz分别为单位质量流体的质量力f沿x，y，z三个方向上的分量，z轴垂直向上。

将方程(1)～(3) 沿流线积分即可得到伯努利方程[7]。由流线方程

可得到uydx=uxdy，uzdx=uxdz，所以式(1)乘以dx后可写为

式中，u2/(2g) 为单位重量流体的动能，z为单位重量流体的重力势能，p/(ρg) 为压力对单位重量流体所做的功。理想流体沿着流线定常流动时，单位重量流体的动能、势能和压力做功之和为常数。这三种形式的能量和功在流动的过程中是可以转化的，伯努利方程是能量转化与守恒定律在流体力学中的具体反映[7]。

此外，也可以根据兰姆运动微分方程进行推导[8]。兰姆运动微分方程为欧拉运动微分方程的另外一种表达形式，优点是对于无旋流动时，方程可以大大简化，此处不再赘述。

2.2 推导方法二

在理想流体的定常流动中，考虑沿流线方向作用于流管中一个微元上的力，并对此微元应用牛顿第二定律(图7)。垂直于流线的此微元截面积具有任意的形状，其面积大小由dA变化为dA+o(dA)。忽略二阶小量后，微元的质量为

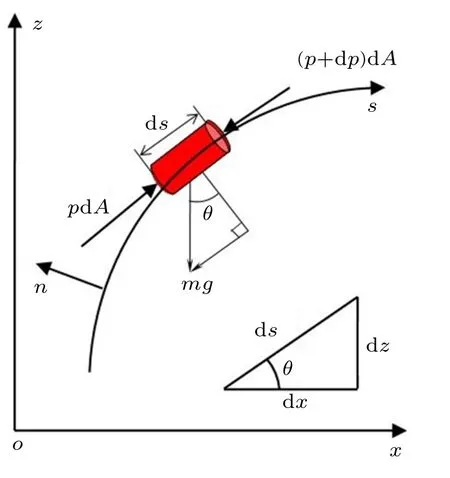
图7 沿流线运动的微元

沿流线切线方向进行受力分析，理想流体无切应力，则表面力为

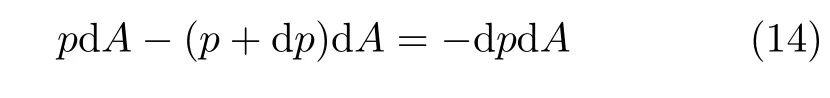
重力场中，重力在流动方向上分量为

式(17)与式(10)相同，适用于可压流体和不可压缩流体。在不可压缩条件下积分即可得到常见形式的伯努利方程。式(17) 通常也称为一维欧拉方程，是列奥纳德·欧拉(Leonhard Euler) 于1750 年首先导出。此方法的优点在于学生未掌握欧拉运动微分方程时也能够较好理解伯努利方程的推导过程。

2.3 推导方法三

在理想流体定常流动中，任取一微流束，取1-2 段作为控制体进行分析(图8)。假设在t时刻，流体系统与控制体重合，在t+ dt时刻，流体系统运动至1′-2′位置。微流束在过流断面1-1和2-2 处的面积，压强，流速，密度，高度分别为dA1，dA2，p1，p2，u1，u2，ρ1，ρ2，z1，z2。对不可压缩流体，ρ1=ρ2。

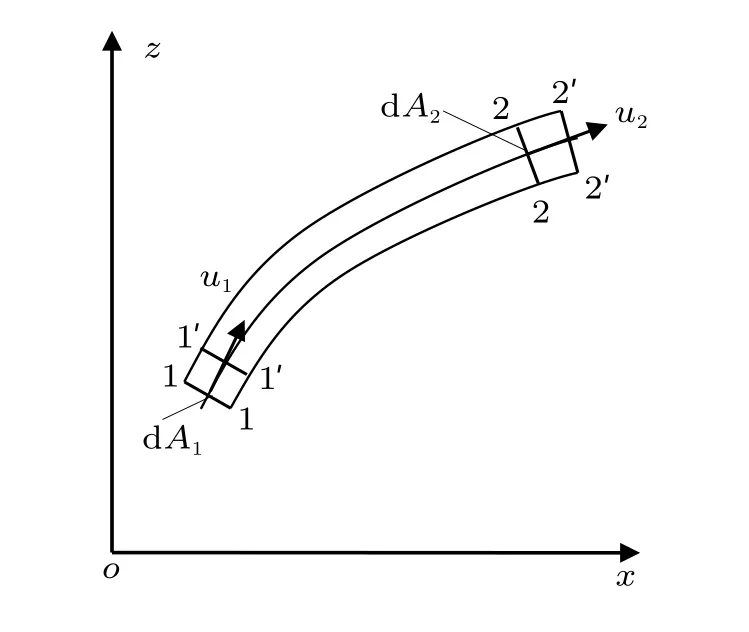
图8 定常流场中的微流束

由定常不可压缩条件知，微流束在1-1′和2-2′段的体积相等，用dV表示。忽略二阶小量，流体从1-2 移动到1′-2′外界压力对系统做功

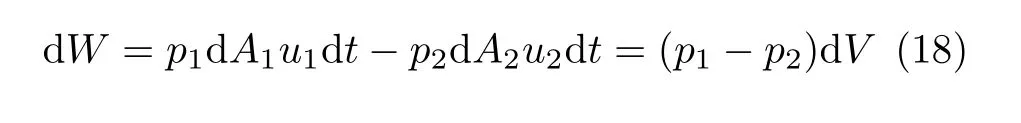
流体从1-2 段运动到1′-2′位置时机械能的增量

与前两种推导方法不同，方法3 是基于功能原理推导得到。方法3 比较简洁直观，适合基础比较薄弱的学生掌握。

2.4 伯努利方程中压强的物理意义

由以上推导过程可知，伯努利方程中z代表了重力对单位重量流体所做的功，表示单位重量流体的重力势能。p/(ρg) 代表了压力对单位重量流体所做的功，为方便理解，部分中文教材也称之为单位重量流体的压强势能(简称压能)，属于一种机械能。学生在课堂学习时可能遇到以下困惑：压强是一种势能吗？固体有没有压强势能？

为避免学生产生困惑，大多数英文教材中关于伯努利方程中压强项的物理意义并未过多解读[9]。教材[10]将伯努利方程(12)左边三项分别称为单位重量流体的动能，势能和可逆的压强功。教材[11] 中将压强项称为压头，且指出一般不称其为压力能。流体中存在压力做功，这是由于流体在压力作用下可以流动做功，它是流体中一种特殊的能量，固体则没有这种特性。此外，某一空间点处单位重量流体的压能容易求得(不可压缩条件下为p/(ρg))，但对于一个系统中的压能通常难以积分求得，这也限制了将压强项作为一种能量来处理应用，因此在推导方法3 中将压强影响作为力而非能量来考虑。

3 伯努利方程的联系与拓展

伯努利方程与流体力学课程中的其他内容有着密切的联系(图9)。如流体静止时，伯努利方程退化为静力学基本方程；考虑黏性流体管内流动损失时，可以建立黏性总流伯努利方程。如果在课程中引导学生建立点线面的知识体系将有助于加深学生对整个课程的理解和认识。

图9 伯努利方程的知识联系

文献[12] 阐述了伯努利方程在流体静力学、定常孔口出流、毕托管测速、文丘里管流量和翼型绕流等具体流动中的成功应用。公元前250 年，阿基米德提出了流体力学浮力定理。而流体静力学基本方程正是伯努利方程在速度为0 时的特殊形式。1653年，帕斯卡发现的流体压强传递特性也是伯努利方程的一个特殊形式。1643 年，意大利科学家托里拆利通过实验的方法总结出了定常孔口出流的基本公式。流体质点从自由液面运动到孔口，重力势能转化为动能，其机械能守恒的思想与伯努利方程不谋而合。利用伯努利方程的原理还可以通过毕托管测速或文丘里管测流量。值得注意的是，毕托管测速仪的发明时间早于伯努利方程的提出时间，而文丘里流量计发明时间明显晚于伯努利方程的提出时间。从中我们可以看到，实验和理论分析是科学研究的两个重要方法，且相辅相成，相互促进。知识的发现并非一蹴而就，各知识之间蕴含着丰富的联系。

伯努利方程可以在定常、沿流线、无黏、不可压缩、重力场的条件下推导得出。若流线上两点高度相等或者重力可忽略时，伯努利方程也可以写为