含阻尼多裂纹Euler–Bernoulli 曲梁强迫振动的Green 函数解1)
2021-12-31李思谊李映辉
赵 翔 李思谊 李映辉
*(西南石油大学土木工程与测绘学院,成都 610500)
†(西南交通大学力学与工程学院,成都 610500)
近年来,曲梁凭借着承载力高,造型独特等特点广泛应用于现代结构工程中[1-2],例如涡轮等高速机械构件、飞机机身、潜艇与舰船的外壳以及许多轻型的结构和桥梁[3]。Fu 等[4]提出了由曲梁单元组成的网格结构的设计策略,为机械超材料开发提供了理论依据。Huang 等[5-6]对复合材料薄壁曲梁的稳定性进行了分析,并考虑弹性约束的边界条件,分析了复合材料层合曲梁的非线性稳定性。曲梁的振动分析一直是国内外研究的热点问题。Chidamparam 等[7]研究了预应力静力平衡状态下平面曲梁、圆环和拱的自由振动问题。Riedel 等[8]研究了中间弹性支承的双跨Euler–Bernoulli 曲梁的自由振动响应。赵翔等[9]运用Laplace 变换法,研究了Timoshenko 曲梁在强迫振动下的Green 函数。何燕丽等[10]运用Green 函数法求解了曲梁压电浮能器Prescott 模型的Green 函数解。此外,有限元法[11-13]在研究曲梁动力分析中也被广泛采用。
梁构件的损伤问题在实际工程中普遍存在,梁结构通常带裂纹工作[11]。裂纹的存在会降低结构的刚度,从而影响结构的动力特性(固有频率、振型和阻尼比)[14-15]。因此,研究带裂纹曲梁在外激励作用下的动力特性具有实际意义。目前针对多裂纹Euler–Bernoulli 曲梁(Euler–Bernoulli curved beam,ECB) 强迫振动问题的研究还较少,多数是对含裂纹的直梁振动的研究。Ghondos 等[16]针对含开口裂纹的Euler–Bernoulli 梁的横向振动问题,建立了连续裂纹梁振动理论。Caddemi 等[17-18]求解了含多个集中裂纹Euler–Bernoulli 梁和柱的精确的闭式解。Zhao 等[19]利用裂纹截面的不连续斜率模型和Abu-Hilal[20]的工作,给出了Euler–Bernoulli 梁强迫振动下的格林函数解。Chen 等[21]得到了具有阻尼效应的多裂纹Timoshenko 梁强迫振动的闭式解。
经调研发现,对多裂纹曲梁强迫振动问题的研究十分有限。因此,本文给出了多裂纹ECB 的强迫振动的精确闭式解。根据裂纹截面位置的连续性条件[22]以及Zhao 等[19]和Chen 等[21]的工作建立多裂纹ECB 的Green 函数表达式,式中的未知常数由边界条件确定。验证研究结果的有效性,讨论一些几何物理量的影响。
1 具有阻尼效应的ECB 强迫振动的Green函数
本文研究了半径为常数的多裂纹Euler–Bernoulli 曲梁振动模型,如图1 所示,不考虑转动惯量和剪切变形。梁高h,梁宽b的曲梁梁长为L,半径为R,在x=x0处受到简谐集中力P0eiΩt的作用。假设曲梁模型上存在n个开口裂纹,将曲梁分成了长度为Li(i=1,2,...,n+1) 的n+1 个完整段,根据文献[19] 中提出的坐标系建立方法,在多裂纹ECB 模型中建立n+1 个局部坐标系oixiyi(i=1,2,...,n+1)。另外,采用等效无质量扭转弹簧模型来描述曲梁裂纹位置的力学行为。图1 中,Ji(i=1,2,...,n) 表示第i个裂纹处的等效扭转弹簧的局部柔度,是弹簧刚度Keq的倒数,可表示为
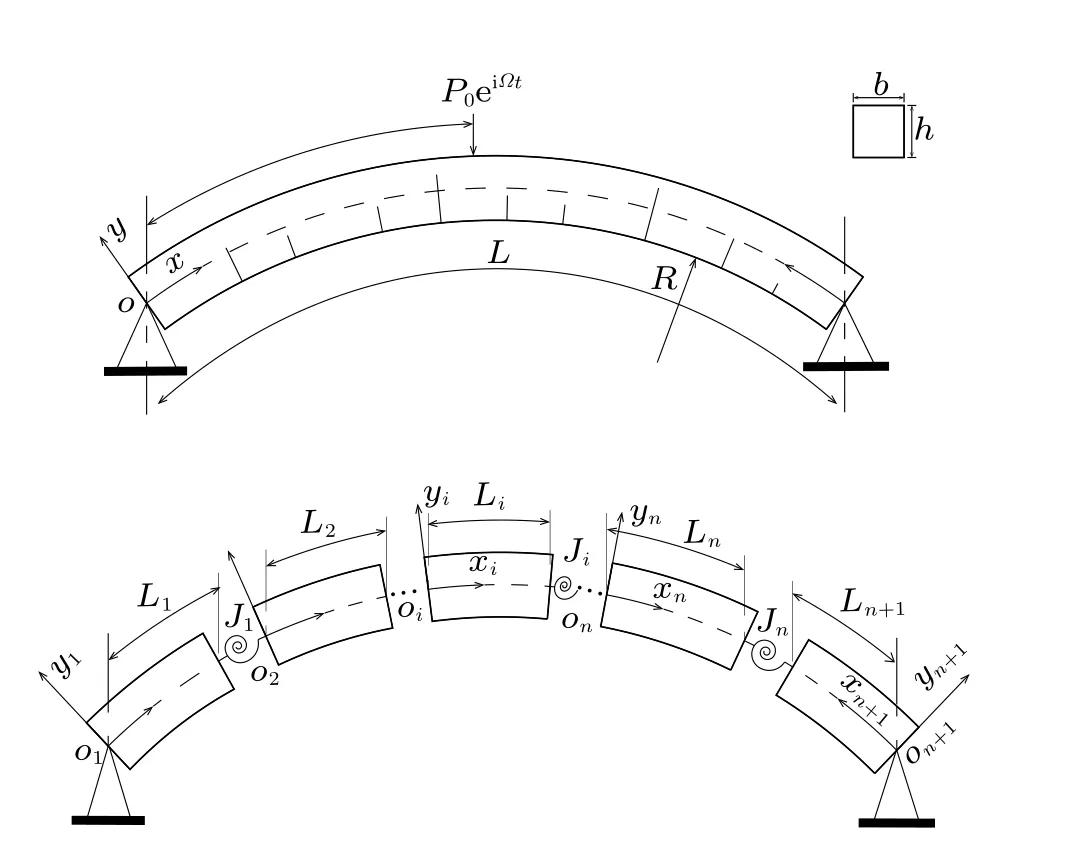
图1 含n 个裂纹的两端简支ECB 在x=x0 处受到简谐力P0eiΩt 作用

其中h′=hc/h是裂纹深度与曲梁高度的比值。
在考虑裂纹影响之前,首先要求解出ECB 强迫振动的Green 函数。根据赵翔等[9]的研究,已经系统地求解出了Timoshenko 曲梁在强迫振动下的稳态Green 函数解。本文在此基础上得到了强迫振动ECB 的Green 函数解。在此对其过程做简单说明。
引入ECB 控制方程[9]
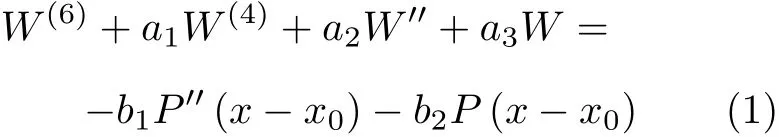
式中W(x)是曲梁的径向位移,W′′,W(4),W(6)是径向位移的各阶导数,P(x) 是曲梁受到的简谐作用力,常数ai(i=1,2,3),bi(i=1,2) 分别定义为[9]
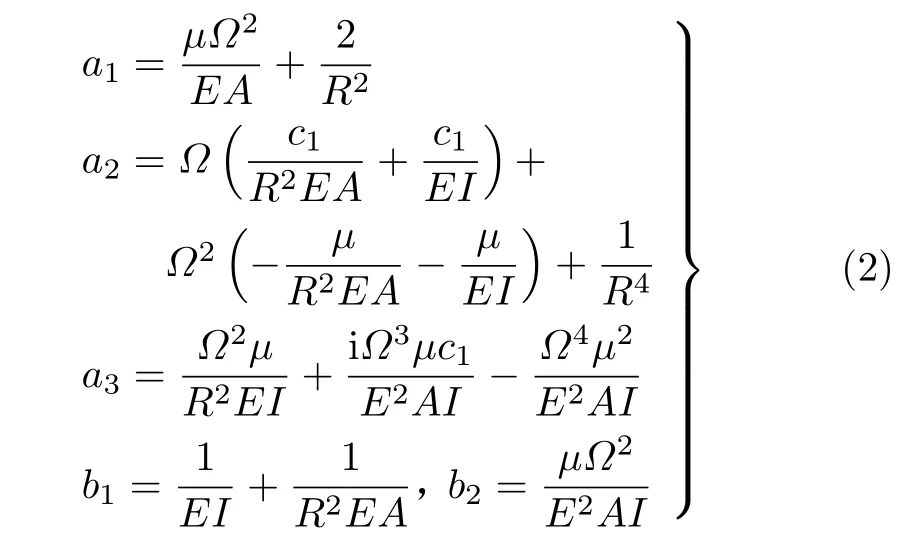
其中c1为阻尼系数,μ是单位长度质量,Ω是外激励频率,A是曲梁横截面面积,E是弹性模量,EI表示抗弯刚度,EA是抗拉刚度。
ECB 的Green 函数G(x;x0) 是指曲梁在x0处受到单位集中力时稳态响应的挠度,是式(3) 的解
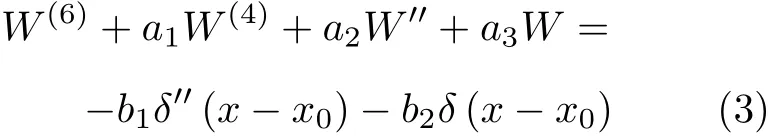
式中δ(·) 是狄拉克函数。
通过叠加原理和Laplace 变换可以得到Green函数
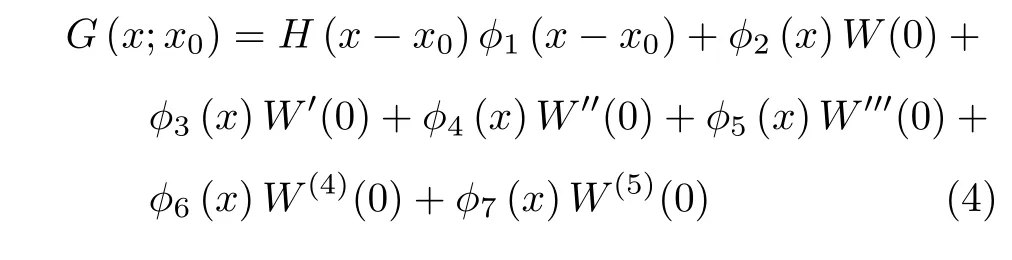
其中,未知常数W(0),W′(0),W′′(0),W′′′(0),W(4)(0),W(5)(0) 分别为W(x) 在x= 0 处的各阶导数,可以由曲梁两端的边界条件确定;H(·)是单位越阶函数;φi(x) (i= 1,2,···,7) 与Ai(x)(i=1,2,···,6) 定义为

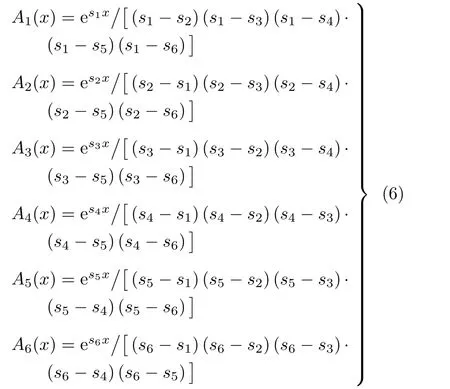
si(x)(i=1,2,···,6) 是式(7) 有关频率Ω的代数方程的根
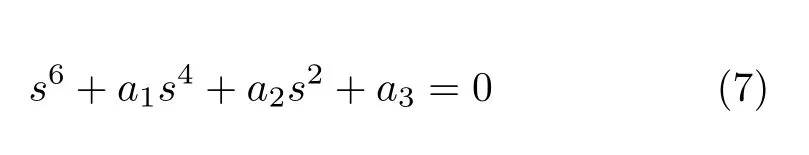
曲梁的动力学分析要比直梁模型复杂很多,需要考虑曲梁的轴向位移、径向位移以及耦合位移等。因此为了研究裂纹曲梁的力学行为,还需要求解出轴向位移V(x) 的Green 函数。Green 函数为

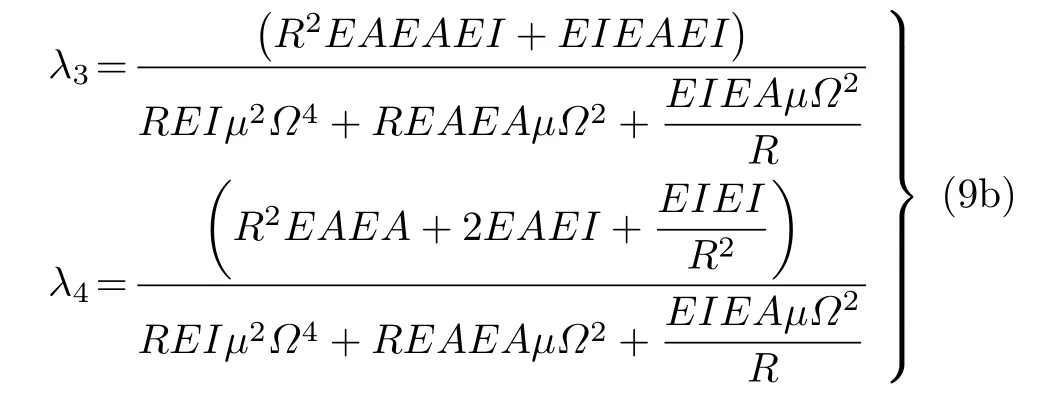
比较式(4)和式(8)发现,轴向位移和径向位移的格林函数的数学形式相同,所含的未知常数也相同,并且这些常数都与零点有关,可以利用这一特征简化计算过程。
2 多裂纹ECB 的Green 函数解
两端简支的曲梁边界条件(轴向位移与径向位移为零,弯矩为零)[22]可以确定位移和力学边界:W1(0) = 0,V1(0) = 0,W′′1(0) = 0,Wn+1(0) =0,Vn+1(0)=0,W′′n+1(0)=0。
局部坐标系下的Green 函数 ¯Gi(xi;xi0) (i=1,2,···,n+1) 表达式为

2.1 裂纹截面处的转换关系

其中F(x),M(x),Q(x) 是曲梁的轴力、弯矩以及剪力,θ(x) 是截面转角,分别为


由式(15) 可知,在第i(1 ≤i <n) 裂纹截面处的转移关系可由式(17) 获得

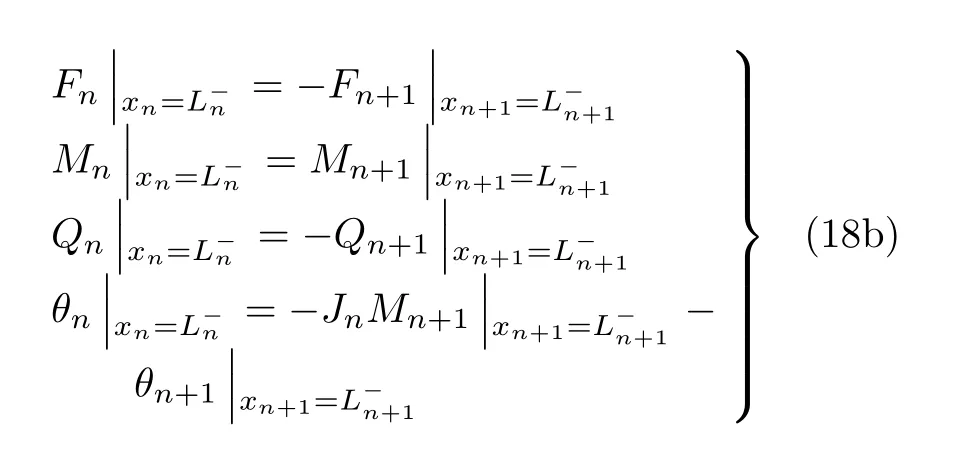
将式(10) 代入式(18) 得到
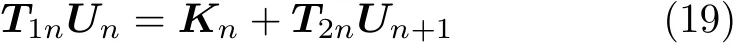
其中
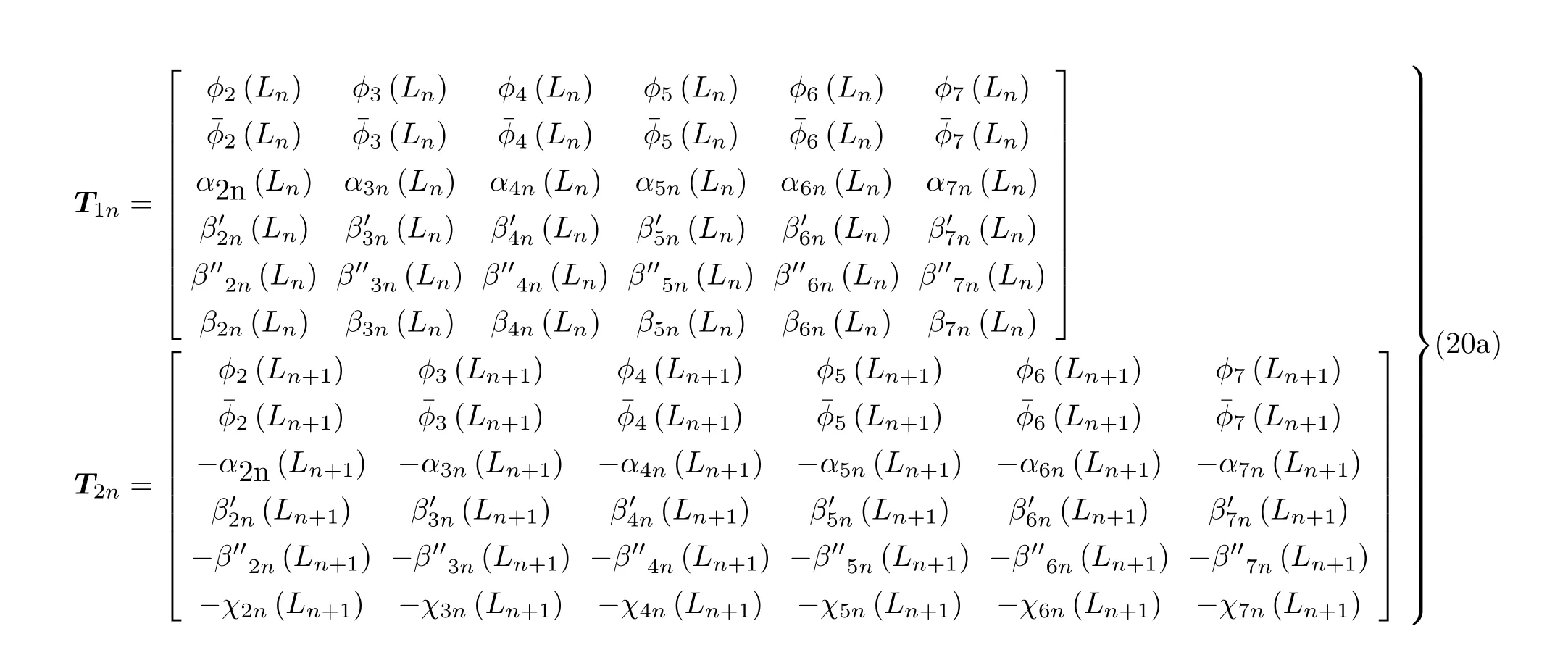

另外

2.2 确定未知常数

ECB 被裂纹分成的每一段都有6 个未知常数,共有6n+6 个未知常数需要定义。曲梁在左端x=0处的边界条件可以把第1 段的6 个未知常数减少至3 个,同样在右端x=L处的边界条件可以把第n+1段的未知常数减少到3 个。最后由转换关系式(17)和式(21) 确定其余常数,从而得到一个只含有6 个未知常数的方程。
裂纹曲梁第1 段和第n+1 段的未知向量为

由式(17) 可知,U1和Un的关系为
将式(23) 代入式(21) 得到
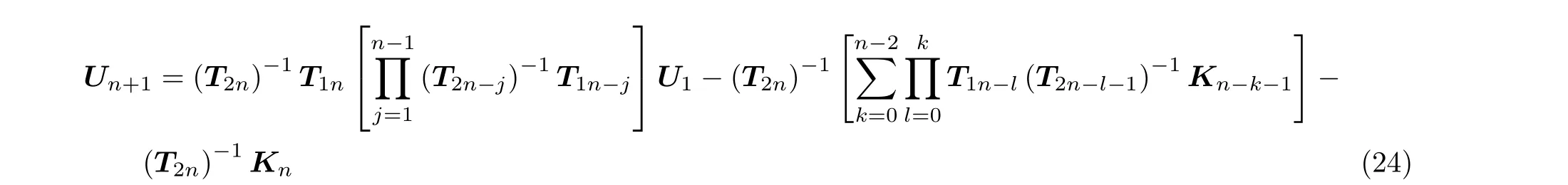
式(24) 已经完成了减少变量的过程,是只有六个未知常数D1,E1,F1,Dn+1,En+1,Fn+1的方程,其余向量Ui(i=2,3,···,n)可通过式(17)定义。另外推导出含n个裂纹曲梁的频率方程,如式(25)
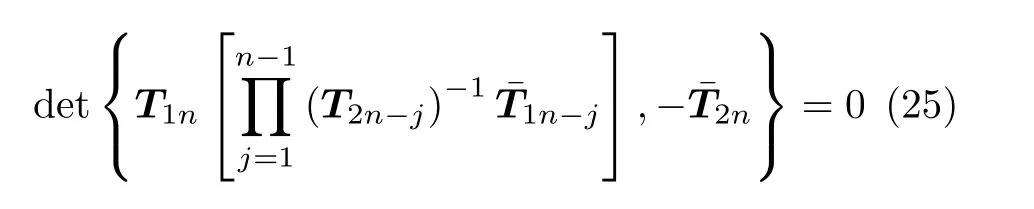
其中
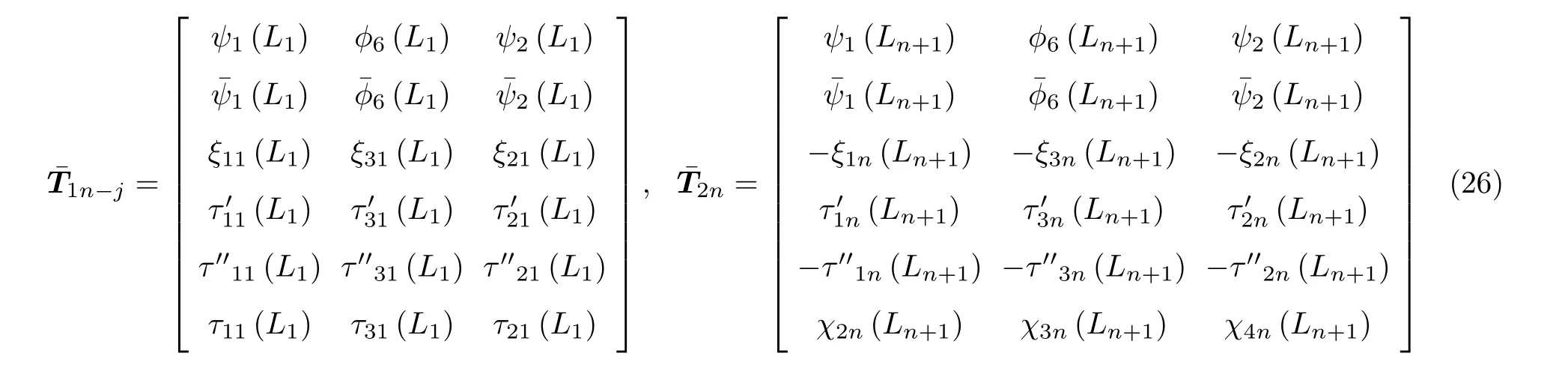
式中,
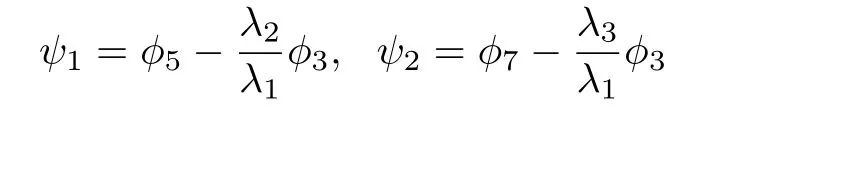
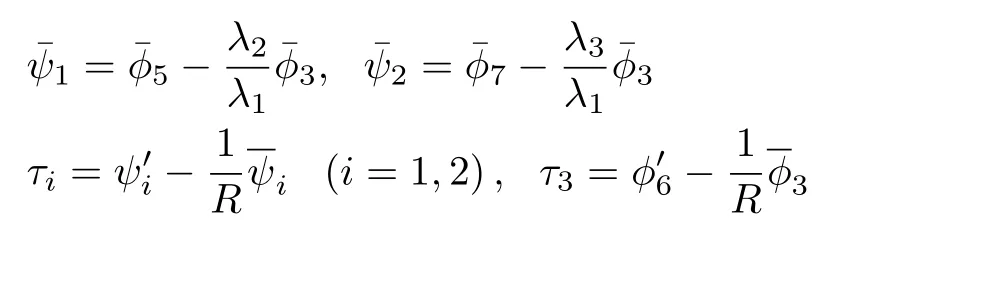
2.3 坐标变换
3 数值结果与讨论
在本节中,考虑一个两端简支的ECB,在x=2/L处受到单位简谐集中力作用。为了方便起见,引入无量纲化参数

3.1 解的有效性验证
本小节验证了多裂纹ECB 强迫振动解析解的有效性。在上文中已经提到使半径趋于无穷大,ECB的Green 函数解可以退化为EB 的Green 函数解,因此将本文的退化解与文献[19] 进行对照。如图2所示,设定相同的材料参数与裂纹参数,对照结果表明本文结果的退化解与文献[19] 中的结果基本一致。但存在些许误差,原因是曲梁半径无穷大不可能真实存在,本文设置R= 10 000 m 得到的结果已经与文献基本吻合。因此这一误差并不影响本文解的有效性验证。另外还建立了两端简支EB 的有限元模型,对比了本文的退化解与有限元算例的位移解,结果基本吻合,从而进一步验证了解的有效性。

图2 在简谐激励下梁稳态响应时各点简谐运动的幅值曲线(h′ =0.2)
3.2 几何物理参数对ECB 振动响应的影响
本节内容分别分析了裂纹深度、裂纹位置、曲梁半径对振动响应的影响以及双裂纹之间的相互影响。
图3(a) 和图3(b) 所示是以裂纹深度h′和裂纹位置L′为自变量时的无量纲化的挠度g(ξ;0.5),其横坐标是无量纲化的曲梁的跨度ξ,从图中可以看出挠度随着裂纹深度h′和位置L′的增大而增大。从物理意义看,曲梁上产生最大挠度的位置也发生了变化,如果裂纹深度较大或者裂纹位置较靠近跨中,裂纹处的挠度就会大于跨中挠度;相反,裂纹深度较小或者裂纹位置远离跨中,曲梁的最大挠度仍在跨中产生。
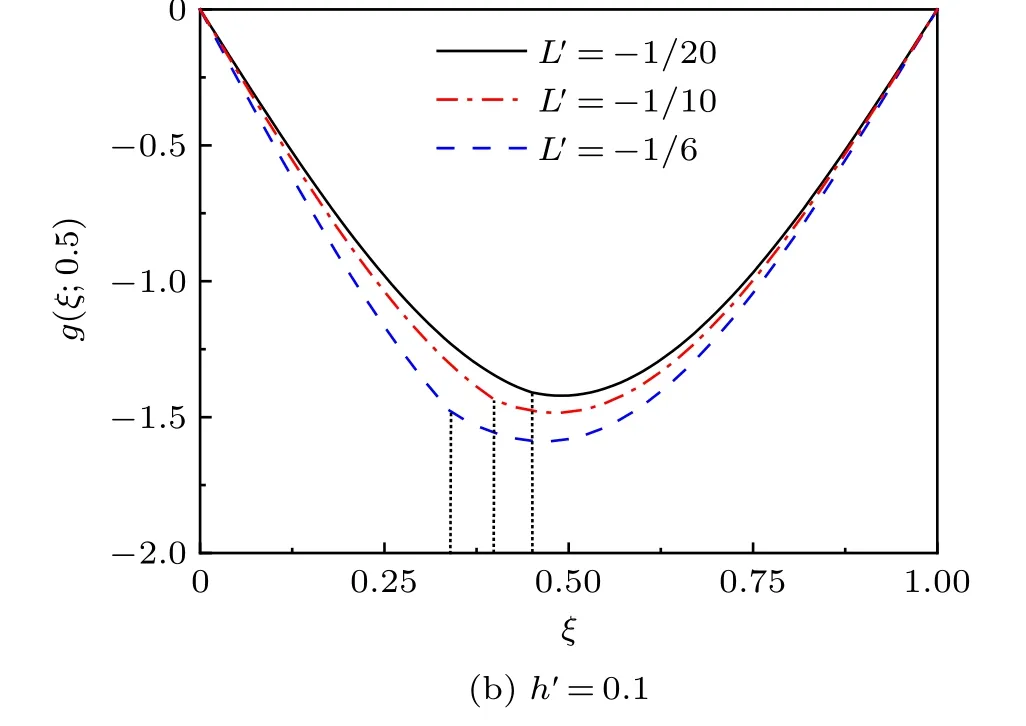
图3 ECB 的无量纲化位移g(ξ,0.5)(R =2,垂直虚线表示裂纹位置)(续)
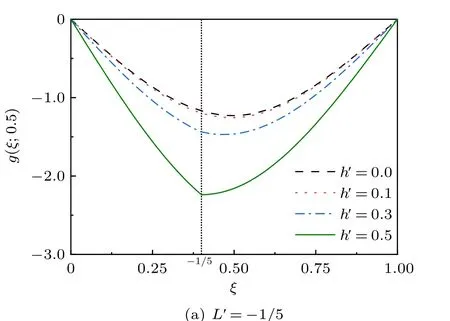
图3 ECB 的无量纲化位移g(ξ,0.5)(R =2,垂直虚线表示裂纹位置)
图4 是不同半径下的ECB 无量纲化的挠度g(ξ;0.5),其横坐标是无量纲化的曲梁的跨度ξ。从图中可以看出,随着半径的减小,ECB 的挠度逐渐减小,最大挠度也逐渐接近裂纹位置。
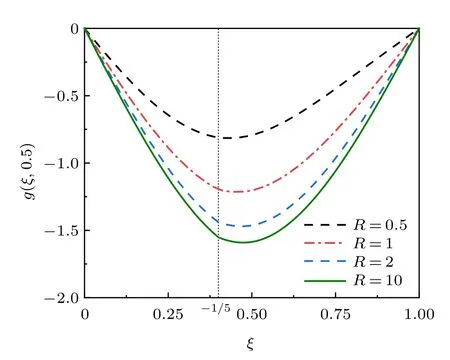
图4 不同半径下ECB 的无量纲化位移g(ξ;0.5) (h′ =0.3,垂直虚线表示裂纹位置)
假设两个裂纹深度相同并且在曲梁上的位置中部对称,可表示为±L′(0 ≤L′≤0.5)。为了研究双裂纹曲梁中两个裂纹之间的相互作用,引入两个裂纹深度相同的单裂纹梁,位置表示为+L′,-L′。图5 所示是ECB 无量纲化的挠度g(ξ;0.5),其横坐标是无量纲化的梁的跨度ξ。图中填充区域的面积表示两个裂纹之间相互作用的强度,面积越小,挠度g(ξ;0.5;±1/5) 和gsum(ξ;0.5) 之差越小,相互作用越明显,反之亦然。

图5 ECB 的无量纲化位移g(ξ;0.5)(h′ =0.3,垂直虚线表示裂纹位置)
4 结论
本文研究了多裂纹ECB 强迫振动的Green 函数解,适用于不同边界条件下的ECB。数值计算中,通过将多裂纹ECB 退化解与多裂纹EB 模型文献解和有限元算例的位移值比较,验证了解的有效性。通过探究裂纹深度、裂纹位置、曲梁半径对曲梁挠度的影响,得出以下结论:(1) 随着裂纹深度和裂纹位置的增加,ECB 的无量纲挠度逐渐变大;(2) ECB 无量纲挠度随着半径的增加而增大;(3)以双裂纹梁为例,研究了裂纹之间的相互作用,用响应挠度曲线之间的面积表示了相互作用的强度。文中所研究的理论公式可为相关领域的分析和计算提供理论参考。
