开槽型盘式异步磁力耦合器调速特性

2021-12-29杨超君朱莉吴盈志彭志卓邰蒋西张磊

电机与控制学报 2021年11期

杨超君，朱莉，吴盈志，彭志卓，邰蒋西，张磊

(江苏大学机械工程学院，江苏镇江 212013)

0 引言

异步磁力耦合器可通过气隙的调控来控制输出转矩及转速，适用于多种工况，能够避免传统传动方式中的摩擦磨损问题，具有节能性及过载保护和软启动等功能，多用于石油、化工等环境恶劣的领域。异步磁力耦合器在机械传动中表现出的优势引起了众多磁力传动相关方向学者的重视[1-7]。

国内外许多学者针对异步磁力耦合器做了相关研究，Lubin T等[2]应用矢量磁位法推导出盘式异步磁力耦合器的轴向力和转矩的解析表达式，并分析了磁场分布；Mohammadi等[3]应用等效磁路法推导出盘式磁力耦合器磁通密度及转矩的表达式；Vahid Aberoomand等[4]应用等效磁路法推导出双面永磁轴向涡流耦合器的转矩公式；东华大学朱姿娜等[5]建立了具有多对弧形永磁体结构的磁力耦合器的转矩解析模型，对转矩参数进行了分析；沈阳工业大学张炳义等[6]应用区域划分法对磁力耦合器的漏磁导进行计算。上述研究致力于耦合器转矩及磁场理论公式的推导，为异步磁力耦合器的性能研究奠定了理论基础，但未建立异步磁力耦合器的转差率或输出转速与气隙之间的关系(即调速关系)，无法通过气隙厚度的定量调节控制从而达到实现速度或负载的调节。江苏大学杨超君等[7-13]多年来针对多种结构的磁力耦合器的结构参数与传动性能、磁场分布以及节能方面进行研究，在此基础上，近年来也开展了机械特性、调速性能的探讨，率先提出了调速关系模型及调速特性的研究。其中，文献[7-10]分别建立了实心筒式、实心盘式、鼠笼筒式以及鼠笼(即开槽型)盘式等各类磁力耦合器在恒转矩负载工况和变转矩负载工况下的调速关系式。但是，上述文献中对开槽型盘式异步磁力耦合器(slotted-type axial-flux asynchronous magnetic coupler,SAAMC)调速特性的研究尚不全面，仍需深入分析探讨。

为解决SAAMC的实际调速问题，本文以一台18极16槽的SAAMC样机为例，分析其磁路结构特点，采用等效磁路法推导出其转矩表达式，并建立恒转矩负载、二次方率负载，尤其是恒功率负载工况下的调速关系计算模型，模拟获得机械特性、调速特性曲线，特别是功率特性曲线，并对三种负载下的调速性能进行分析，以及对其进行试验研究，分析工作参数对SAAMC调速性能的影响，验证理论模型的正确性。

1 电磁转矩及调速关系模型

1.1 基本结构及调速机理

SAAMC的结构模型如图1所示，导体转子由导体及轭铁两部分组成，导体加工有扇形槽，装配于导体轭铁的齿上，呈现轭铁与铜导体的交替排列。永磁转子由轴向均匀充磁的扇形永磁体与轭铁组成，扇形永磁体沿周向N、S极交替排列，安装在轭铁表面。其调速模型如图2所示，假设以永磁转子作为主动转子，当电机带动主动转子转动时，主动转子和从动转子之间产生转速差，导体转子切割磁力线产生感应电流，感应电流产生的感应磁场与原永磁磁场耦合实现扭矩传递。磁力耦合器的结构参数及材料属性见表1和表2。

图1 磁力耦合器结构模型Fig.1 Structural model of the magnetic coupler

图2 磁力耦合器调速模型Fig.2 Speed-control model of the magnetic coupler

表1 磁力耦合器结构参数Table 1 Structural parameters of the magnetic coupler

表2 磁力耦合器材料属性Table 2 Material properties of the magnetic coupler

1.2 电磁转矩计算公式

为计算SAAMC的电磁转矩，本文运用等效磁路法对电磁转矩公式进行推导。将磁力耦合器在永磁体平均半径处沿周向展开，从而在此二维展开模型上分析磁力耦合器的磁通路径。

为便于磁通路径分析，在进行磁场转化为磁路时，做以下假设：

1)主磁通量垂直通过永磁体、气隙和导体盘；

2)仅考虑耦合器永磁体产生的磁场，不考虑感应磁场对原磁场的影响；

3)忽略外界条件对材料性能的影响，故磁路中各组成部分的材料性能保持不变；

4)磁路中轭铁不发生磁饱和，永磁体的磁导率与导体的电导率均为定值。

图3为磁力耦合器的磁通路径，主要由3个部分组成：主磁路Ⅰ、相邻磁体间漏磁路Ⅱ及单个永磁体侧面的漏磁路Ⅲ。

根据图3所示的磁通路径，建立SAAMC的等效磁路模型，由于该磁力耦合器的导体盘上存在齿槽，导体与轭铁交错排布，在耦合器工作的过程中，铜导体层上的磁通路径经过轭铁和铜两个磁导率不同的部分，计算铜导体层磁阻时，需要对轭铁和铜的磁导率进行等效计算。图4为磁力耦合器的等效磁路模型，其中，Fm为永磁体磁动势，Φ为总磁通，Φ0为主磁通，Φ1为漏磁通，R0为永磁体磁阻、R1为气隙磁阻、R2为铜导体磁阻、R3为铜导体轭铁磁阻、R4为永磁体轭铁磁阻、R5为相邻两磁极间漏磁阻、Rmi为永磁体单侧漏磁阻。考虑到本文所研究的耦合器中永磁体为紧密排布，漏磁路Ⅲ对整个磁路的影响甚微，所以永磁体单侧漏磁阻Rmi可以忽略不计。

图3 磁力耦合器磁通路径Fig.3 Magnetic flux path of the magnetic coupler

图4中，Fm为永磁体的磁动势源[13]，表达式为

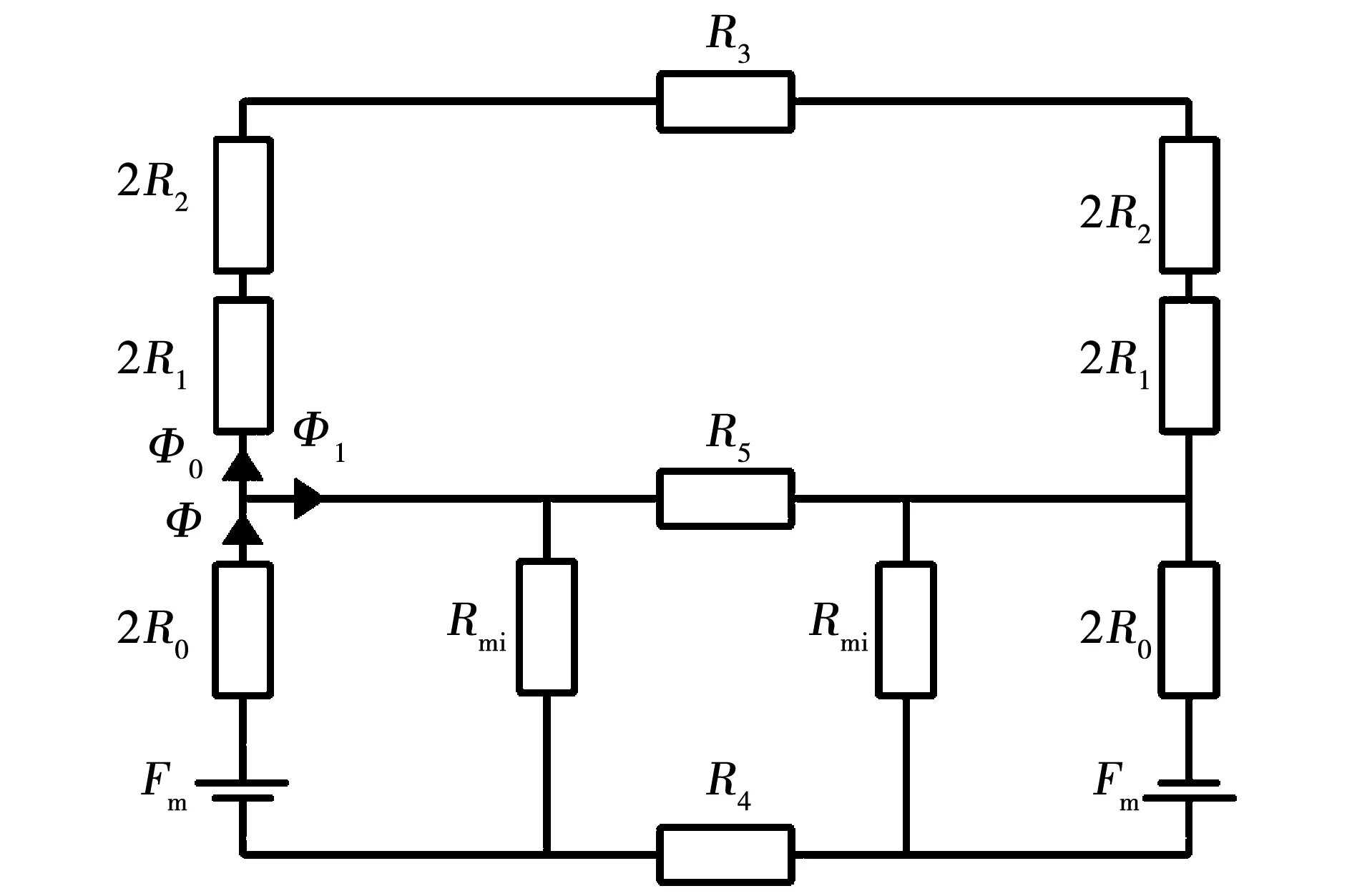
图4 磁力耦合器等效磁路模型Fig.4 Magnetic equivalent circuit model of the coupler

Fm=Hchm。

(1)

根据磁阻计算公式，得到永磁体磁阻、气隙磁阻、铜导体磁阻、铜导体轭铁磁阻、永磁体轭铁磁阻及漏磁阻[14]分别为：

(2)

(3)

(4)

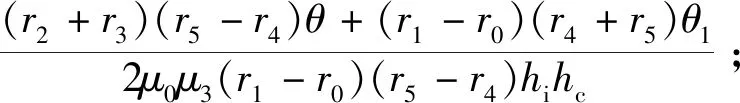
(5)

(6)

(7)

式中：μ0为真空磁导率；μ1为永磁体相对磁导率；μ2为导体层的等效磁导率；μ3为轭铁的相对磁导率；θ为单个永磁体的圆心角；θ1为齿槽的圆心角；θ2为铜导体的圆心角，如图1所示。

由于铜导体与轭铁形成交替排列，导体的磁导率需进行等效计算，其等效磁导率[15]为

(8)

根据基尔霍夫定律，等效磁路模型中各物理量之间的关系为：

(9)

将式(2)～式(7)代入到式(9)，可得

Φ0(g)=

(10)

根据磁通密度的计算公式，SAAMC关于气隙g的平均气隙磁通密度表达式为

(11)

为了考虑磁力耦合器实际运行时，齿槽对原磁场的影响，引入鼠笼电机中的卡特系数[16]，得到磁力耦合器的卡特系数为

(12)

其中：

(13)

式中：Bg为修正后气隙磁密；σm为槽宽缩减因子；δ为单个扇形导体的平均弧长；λ为单个扇形导体及其相邻两个扇形轭铁的平均弧长之和，见图3。

根据文献[2]中的电磁转矩计算方法，结合式(12)，并考虑三维端部效应，得出磁力耦合器的电磁转矩T关于气隙厚度g的计算公式为：

(14)

其中：

(15)

式中：KR为三维校正因子；σ为铜层的电导率；s为转差率；p为永磁体的极对数；n0为输入转速；Kcm为卡特系数；m、α和γ均为自定义参数；Δl为导体延伸长度。

1.3 调速关系计算模型

由调速原理可知，磁力耦合器可以通过调节转子间的气隙厚度g来控制输出转速nout，并将调速过程中转子间的气隙厚度g与输出转速nout或转差率s间的关系定义为磁力耦合器的调速关系。本节在1.2节的基础上，将建立恒转矩负载、二次方率负载和恒功率负载三种工况下的调速关系模型。

1)恒转矩负载调速关系模型。

恒转矩负载设备有传送带、轧钢机、提升机等，负载转矩为定值，即T(g)=Tload=Tc，则

(16)

其中：

(17)

2)二次方率负载调速关系模型。

(18)

3)恒功率负载调速关系模型。

恒功率负载设备有造纸机及机床主轴等，负载转矩与转速成反比，即T(g)=Tload=9 550P/nout，则

(19)

运用数值分析软件，对以上3种工况下的调速模型进行离散化求解，可得到其调速特性。

2 电磁场及调速特性仿真分析

为了验证电磁转矩及调速关系的数学模型，本文运用有限元软件对SAAMC进行三维建模与仿真分析。

2.1 三维模型建立

图5为在有限元分析软件中建立的SAAMC的三维模型，其结构参数和材料属性分别见表1、表2。三维模型建立后，对其进行网格划分及求解设置。

图5 磁力耦合器三维模型Fig.5 3-D model of the magnetic coupler

2.2 气隙磁场仿真分析

图6为气隙厚度为6 mm时耦合器永磁体的磁场强度云图，可以发现永磁转子的磁场强度整体上大于铜转子磁感应强度。永磁转子上磁场强度在两永磁体之间达到最大值，导体转子上磁感应强度在齿槽边缘达到最大值。图7为气隙厚度为6 mm、输入转速1 200 r/min、转差率10%时的瞬态磁感应强度云图，永磁转子上磁感应强度略低于永磁体的磁场强度，但分布规律基本一致。

图6 永磁体的磁场强度云图Fig.6 Magnetic field intensity nephogram of permanent magnet

图7 瞬态磁感应强度云图Fig.7 Transient magnetic induction intensity nephogram

2.3 机械特性与功率特性仿真分析

SAAMC的结构参数及工作条件确定时，将电磁转矩与输出转速、转差率之间的关系曲线(nout=f(T)或T=f(s))称为机械特性曲线，将输出功率与转差率之间的关系P=f(s)称为功率特性。图8为输入转速1 200 r/min，气隙厚度为1 mm下的机械特性曲线，当负载转矩小于启动转矩Tst时，磁力耦合器启动。启动后，电磁转矩先增大后减小，转差率为sm时，电磁转矩达到最大值Tm，即(Tm，sm)为磁力耦合器的最大转矩点。从模拟结果可以发现不同气隙厚度下，最大转矩点的转差率均为sm=15%(见图10)。图9为输出功率随转差率变化的曲线，可见气隙厚度为1 mm时，在转差率sP1=11%处达到最大功率值Pm=20.35 kW，即(sP1，Pm)为气隙厚度1 mm时的最大功率点，气隙厚度为14 mm时，在sP2=13%处达到最大功率值Pn=2.26 kW，即(sP2，Pn)为气隙厚度14 mm时的最大功率点。可见，磁力耦合器最大转矩点的转差率固定不变，最大功率点的转差率随着气隙厚度的增大而略有增大，处于sP1～sP2范围。且运行转差率小于最大转矩点或最大功率点处转差率时，转矩或功率随转差率减小而减小的速度较快，反之则较慢。另外，由各曲线间的距离可以看出，最大转矩值和最大功率值均随气隙厚度的增大呈非线性减小，减小速度先快后慢。所以需要较大转矩和功率时，应在较小工作气隙下，选择最大转矩点或最大功率点附近的区间进行调速。

图8 机械特性曲线Fig.8 Mechanical characteristic curve

图9 变气隙下输出功率随转差率变化曲线Fig.9 Variation curves of output power with slip rate under variable air gaps

2.4 调速特性仿真分析

图10为恒转矩负载下的调速特性曲线，可知输出转速区间为n0～nm时，耦合器稳定运行，其中nm为最大转矩点(Tm，sm)处的转速，点a～e属于稳定运行点。若负载由T0增加为T1，将气隙厚度由4 mm减小为2 mm即可以保持输出转速为n1不变，工作点由a点转移到b点；若负载保持为T2不变，将气隙厚度由1 mm增大到2 mm即可以将输出转速由n1调整到n2，工作点由c点转移到d点。即磁力耦合器可以实现两种模式的速度调控：其一为负载转矩值变化时，改变气隙厚度控制输出转速不变；其二为负载转矩值不变时，改变气隙厚度控制输出转速达到目标值。

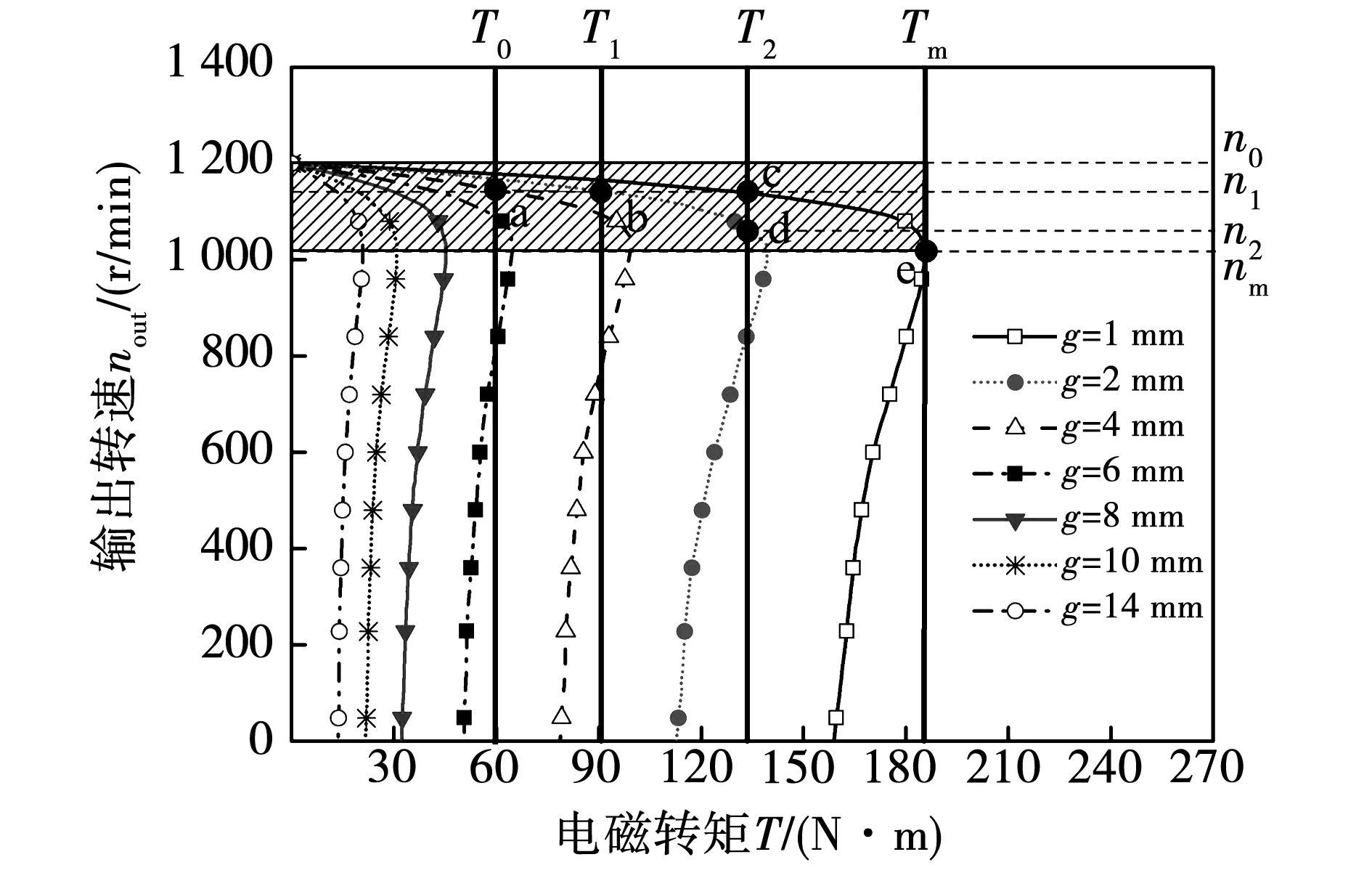
图10 不同气隙处恒转矩负载调速特性曲线Fig.10 Speed-control characteristic curves under constant torque load at different air gaps

图11为二次方率负载下调速特性曲线，系数为k1、k2及k3的二次方率负载曲线与不同气隙厚度下的机械特性曲线的交点处均稳定运行。负载系数为k2=1.59×10-4时二次方率负载曲线与气隙厚度为1 mm的机械特性曲线交于最大功率点N，此时调速区间为0～nk2，可达到最大功率，负载系数减小为k1时，调速区间增大为0～nk1，功率减小较快(如图9)，负载系数增大为k3时调速区间减小为0～nk3，功率减小较慢。可见，以与最小工作气隙的最大功率点相交的二次方率负载曲线的系数为临界值，负载系数越小调速范围越大，功率减小较快，适合小转矩下的大范围调速；负载系数越大，调速范围越小，但功率减小较慢，适合大转矩下的小范围调速。

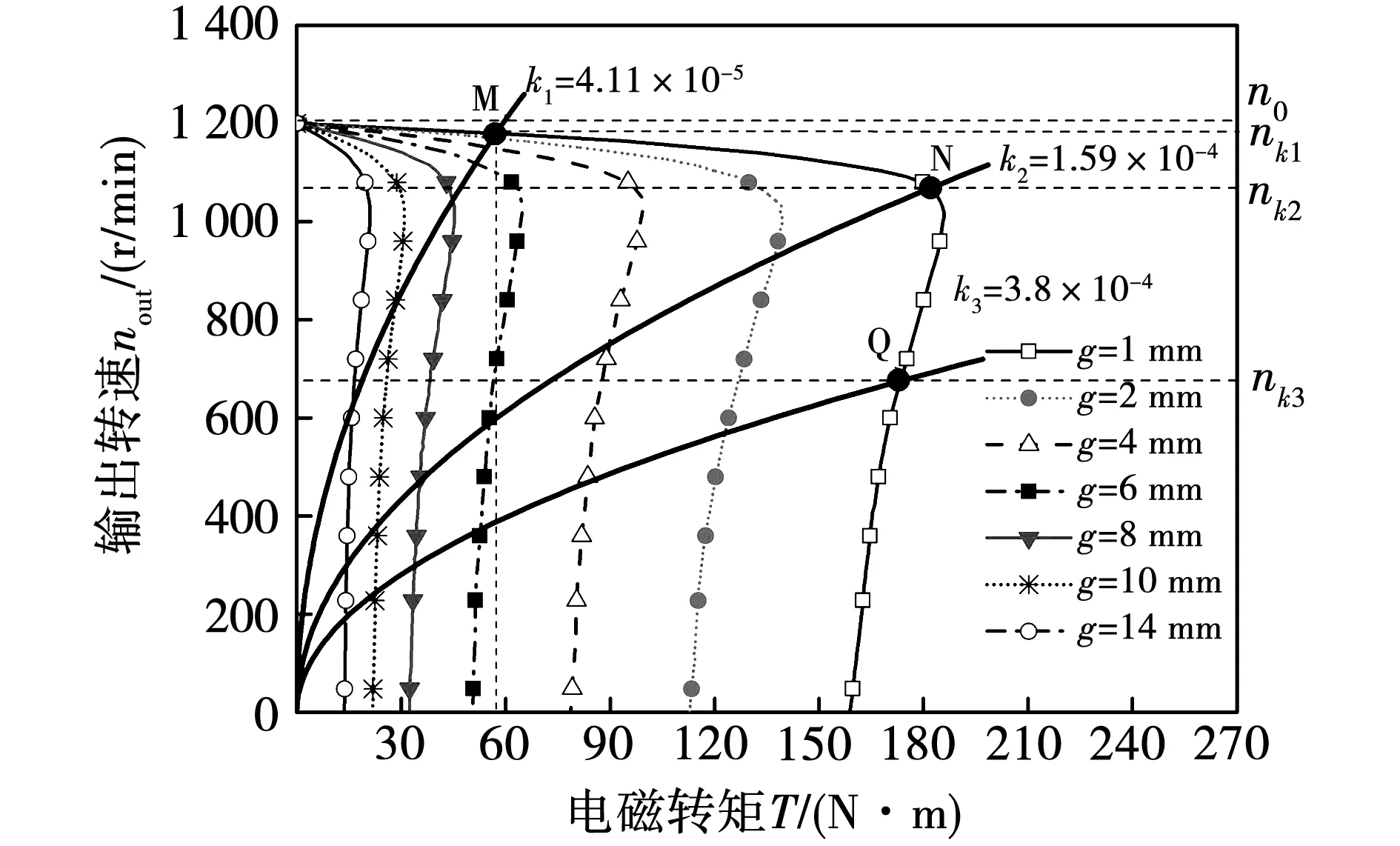
图11 二次方率负载不同气隙下调速特性曲线Fig.11 Speed-control characteristic curves under quadratic rate load at different air gaps

图12为恒功率负载调速特性曲线，f～k为一定气隙时的最大功率点。

图12 恒功率负载不同气隙下调速特性曲线Fig.12 Speed-control characteristic curves under constant power load at different air gaps

图13为图12中方框处的放大图，当转速大于最大功率点对应的转速时，磁力耦合器处于稳定运行区域。恒功率值为P1时，A～E点为稳定运行点，F～J点为不稳定运行点，调速区间为nP1～nP2，可进行调速的气隙范围为1～8 mm。当负载功率值为P2时，K～M点为不稳定运行点，此时可进行调速的气隙范围减小为1～4 mm。当负载功率值增大为P3时，负载曲线与气隙厚度1 mm的机械特性曲线相切于最大功率值点N，仅有N点为稳定运行点，此时无法进行调速。可见，负载功率值越大，可进行调速的气隙范围越小，磁力耦合器可以带动的最大恒功率负载为P3=20.35 kW，与最小工作气隙1 mm处的最大功率值(见图9)相等。

图13 图12中A～E处的局部放大图Fig.13 A local enlargement at points A～E in Fig.12

3 实验验证

为进一步验证电磁转矩及调速关系的计算值与仿真值的准确性，需对磁力耦合器的调速过程进行实验验证，由于实验条件限制，仅对调速过程中的稳态工作点进行实验。

3.1 实验装置

图14为SAAMC的实验平台。平台的动力源为5.5 kW的三相电机，通过变频器控制其输出转速。JC型传感器用于测量磁力耦合器输入以及输出端的转矩和转速，磁粉制动器提供恒负载或风机提供二次方率负载。实验过程中给定负载，改变气隙厚度，测量不同气隙厚度下的输出转速，得到气隙厚度与输出转速和转差率的关系曲线。

图14 负载试验平台Fig.14 Test platform with loads

3.2 实验结果及分析

图15为磁力耦合器输入转速1 200 r/min，使用磁粉制动器提供10 N·m恒转矩负载时，不同气隙下输出转速和转差率的实验值、计算值及模拟值的对比图，三者趋势基本一致。但是，由于实验过程中存在摩擦、振动以及测量误差等不可避免的因素影响，实验值较计算值和模拟值偏小。图16为磁力耦合器输入转速为1 100 r/min时，使用风机提供系数为k=1.025×10-6二次方率负载时，不同气隙厚度下输出转速、转差率的实验值与计算值和模拟值的对比图，当气隙厚度在6～14 mm时，三者趋势基本一致，但当气隙厚度达到14 mm之后出现较大偏差。除上述不可避免的因素影响外，大气隙下磁力耦合器带载能力弱、受摩擦转矩影响更大，也会引起较大偏差。可见，实验结果与计算、模拟结果在小气隙范围内具有较好的一致性，而在二次方率负载下，当气隙厚度较大时，产生的偏差较大，但其偏差小于5%。