基于电感辨识的内置式永磁同步电机电流模型预测控制

贾成禹，王旭东，周凯

(哈尔滨理工大学 电气与电子工程学院，哈尔滨 150080)

0 引 言

永磁同步电机广泛采用的电流控制策略是基于转子磁场定向(field-oriented control，FOC)的单输入单输出比例积分(PI)结合d、q轴电压前馈补偿的电流解耦控制[1-2]。近年来的研究表明，由于模型预测控制(model predictive control ，MPC)算法具有快速的动态性能、以及处理多变量约束的能力等优点，被提出作为永磁同步电机电流控制的一种可行的替代方案[3-5]。由Bemporad等人提出的显式模型预测控制[6](explicit MPC，EMPC)，将多参数规划理论引入状态和输入受二次约束的线性时不变系统的最优化求解中来，用离线求解方式解决多参数规划问题，对约束状态空间分区并设计各区间的显式反馈控制规律，在线计算部分简化为根据系统当前状态，选择实施相应的状态反馈控制律，这种方法把大量计算转移到离线进行，从而克服了传统MPC在线计算量大的缺点，而且有坚实的理论基础，因此受到广泛的关注[7]。

文献[8]提出一种内置式永磁同步电机的显式模型预测电流控制策略，获得了较高的电流环动态性能，设计了在线扰动观测器克服了模型参数变化引起的稳态误差，但是扰动观测器算法较为复杂，在线计算量较大。电机在运行中其参数可能随着温度、磁饱和程度等条件变化，预先设定的固定参数难以实现预测控制算法的理想性能，参数在线辨识是提高控制系统鲁棒性的有效方法，目前应用较广泛的是基于最小二乘法的辨识算法，其结构简单，对叠加白噪声的信号可以实现无偏估计。文献[9]应用RLS算法，实现了对永磁同步电机的定子电阻、永磁体磁链以及d、q轴电感参数的辨识，并用辨识的参数来优化PID参数，能够在电机参数发生变化时快速实现电流的精确控制，但为了使辨识结果收敛，需要施加d轴电流扰动，会影响输出转矩。文献[10]详细讨论了应用RLS辨识算法时“数据饱和”和“测量噪声”对辨识精度和动态性能的影响，并采用改进的递推最小二乘来提高辨识的精度和收敛速度，但是在RLS 中同时引入遗忘因子和加权因子两个可调参数增加了系统调试的复杂度。

为解决传统MPC在线计算量大的问题，本文结合文献[9]和文献[10]的RLS辨识算法并对其进行综合及优化，提出了一种新颖的基于EMPC技术的电流预测控制策略，给出了预测模型和约束条件的线性化方法，以及控制器实现的详细步骤，并设计基于RLS的辨识算法在线辨识d、q轴电感来提高模型预测算法对模型参数误差的鲁棒性，将参数辨识与模型预测控制相结合，获得了高动态响应电流控制效果。

1 IPMSM模型预测控制方法

1.1 线性约束系统的模型预测控制

n个状态变量、m个输入、r个输出的线性系统，其离散时间状态空间模型为：

(1)

其中：x∈Rn为系统状态，u∈Rm为系统输入，y∈Rr为系统输出，满足如下约束：

(2)

其中：H，L和M分别为定义状态和输入约束的矩阵。MPC应用在带有约束条件的线性系统，其控制原理是利用离散时间线性系统模型，在有限的预测时域Np内，以x(k)为系统初始状态，根据系统当前的状态、输入预测系统后续的状态，可以用以下状态方程描述：

(3)

当MPC设计的控制目标为使系统的输出y(k)能够追踪参考输入r(k)时，通常设计为一个二次型的代价函数来评估其性能指标：

r(k))+(u(k+i-1)-

utar(k))TR(u(k+i-1)-utar(k))]。

(4)

其中Np为预测时域，Q>0，R>0是用于惩罚当前状态和控制行为的加权矩阵。通过求解使得代价函数J的值最小，从而得到满足约束条件的控制输入u*(k)。由式(1)～式(4)描述的具有约束条件的有限时域线性系统的最优控制问题可以转化为多参数规划问题，对约束状态空间分区并设计各区间的显式反馈控制律，并可离线求解，这种方法被称为显式模型预测控制(explicit model predictive control,EMPC),可解决在线求解最优化问题计算量大、难以满足实时性的问题。采用EMPC方法得到的最优控制规律是关于当前系统状态参数的线性仿射函数，在每一个约束状态空间分区中，都有如下控制规律：

u*(k)=Kix(k)+ki。

(5)

其中i为当前状态参数向量x(k)所在的约束状态空间区域划分的编号，这样在线计算部分简化为根据当前系统状态参数向量x(k)，确定其在状态空间区域分区上所处的区间号i，由此可获得相应的状态反馈控制律。这种方法把最优化求解转移到离线进行, 在线计算得到极大简化。

1.2 IPMSM数学模型

转子磁场定向的同步旋转坐标系(d-q坐标系)中，星型连接三相永磁同步电机的定子电压方程可以写成如下形式：

(6)

式中：ud，uq为定子电压d、q轴分量;id，iq定子电流d、q轴分量；Rs定子电阻；Ld，Lq分别为d,q轴电感；Ψf永磁体磁链；ωe为转子电角速度。为满足数字控制需要，综合考虑动态模型精度，选取Ts=100μs为时间步长，采用前向欧拉法离散化得到离散时间的模型如下：

(7)

可以写为向量形式的状态空间表达式：

i(k+1)=Adi(k)+Bdu(k)+f(k)。

(8)

其中：

(9)

式中：f(k)代表反电势和交叉耦合效应的影响，在每个采样时刻可由测量的转子转速和交、直电流通过计算得到。选择电流为系统状态，电压为系统输入，在每一个很小的电流环控制周期中，做出如下近似：即在预测时域内认为f(k)是一个常数扰动，即：

f(k+i)=f(k)=fk，i∈{1…Np-1}。

(10)

根据式(8)和假设条件式(10)可以得到线性的系统模型：

(11)

iref(k+i)=iref(k)，i∈{1…Np}。

(12)

通过扩张扰动状态向量f(k)到系统式(11)可以得到该控制系统的线性预测模型：

(13)

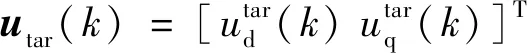
iref(k))+(u(k+i-1)-

utar(k))TR(u(k+i-1)-utar(k))]。

(14)

由于采用显式模型预测控制方法，目标电压向量需要通过选定的状态参数来表达，以便能够离线求解，由式(7)可知稳态时目标电压为：

(15)

当转速较高时，定子电阻的值很小其压降相比于转速相关项的电压可以忽略，求得目标空间电压矢量：

(16)

电流参考值和实时测量的电流反馈值的差值，目标参考电压与当前输入电压的差值在代价函数(14)中都得到了惩罚，从而保证了稳态时系统的实际输出能够准确的跟踪参考输入。IPMSM驱动系统的两个主要的约束条件是d-q平面上的电流和电压的二次不等式约束，其约束条件描述如下：

(17)

(18)

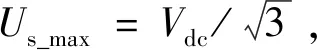
(19)

(20)

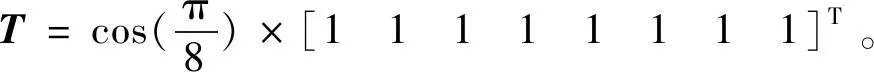
2 电感参数辨识算法

2.1 递推最小二乘法原理

递推最小二乘算法是在前一次估计结果的基础上，利用获取的新的测量数据对前一次估计的结果进行修正，从而递推地得出新的估计值。这样迭代的进行参数估计直到参数的估计值收敛到真实值为止，这种方式在线计算量小且收敛快，可实时在线地辨识出系统的参数。本文基于递推最小二乘方法设计的电感在线辨识算法可以概括为：

θ(k)=θ(k-1)+K(k)ε(k)，

(21)

ε(k)=y(k)-φT(k)θ(k-1),

(22)

K(k)=P(k-1)φ(k)[λI+

φT(k)P(k-1)φ(k)]-1,

(23)

P(k)=[I-K(k)φT(k)]P(k-1)/λ。

(24)

其中，y(k)为输出矩阵；φT(k)为反馈矩阵；θ(k)为系统待辨识的参数矩阵；ε(k)为估计误差，I为单位矩阵，K(k)为增益矩阵，P(k)为协方差矩阵。在测量值都有相同的权重的条件下，随着观测数据的增多递推最小二乘法会出现数据饱和现象，为了防止新数据的作用被旧数据淹没，故引入遗忘因子λ，其作用就是将旧数据按照指数衰减规律逐渐给“遗忘”，从而突出新数据的作用。

2.2 电感辨识模型设计

电感参数值对铁心的饱和程度很敏感，其饱和程度随着d、q轴电流幅值的变化而快速变化。该辨识算法用于快速的辨识出d、q轴电感参数，执行周期与电流环控制周期一致，辨识算法运行过程中保持永磁体磁链Ψf和定子电阻Rs的值不变。又根据d、q轴电流方程(7)选定待辨识参数矩阵为：

(25)

输出矩阵为：

(26)

反馈矩阵为：

(27)

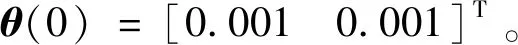
2 仿真与实验

1.5 仿真结果分析

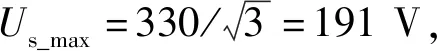
表1 仿真模型的参数Table 1 Parameters of simulation model

图1 系统整体框图Fig.1 Overall system block diagram

图2 电感辨识仿真结果Fig.2 Simulation results of inductance identification

辨识结果的误差率用辨识值与实际值之差的绝对值除以实际值来表达，其结果如图3所示，其稳态误差均小于0.15%，精度较高。在Ld和Lq分别突变的两次动态过程中，d、q轴电感的辨识结果的最大误差分别为6.38%和15.35%，动态过程误差在能接受的范围之内。

图3 辨识误差仿真结果Fig.3 Simulation results of inductance error

验证了电感参数辨识的正确性之后，接下来利用辨识结果来计算扰动项和目标电压，电流环采用EMPC算法对整个系统进行仿真。仿真过程0.6 s，按照表1设定电机参数，给定目标转速5 000 r/min(523.59 rad/s)，在0.25 s时刻d、q轴电流从0 A阶跃到id=-200 A，iq=252 A，保持电流参考值不变直到0.4 s时刻，电流指令以阶跃的方式变化为id=-87 A，iq=146 A。图4展示了d、q轴电流的阶跃响应波形，可见EMPC电流控制器能够提供快速的动态响应，几乎没有超调，稳态后能够准确追踪电流参考值。

图4 d、q轴电流阶跃响应仿真结果Fig.4 Simulation results of d- and q-axis current step response

图5为代价函数值的变化情况，以及状态参数向量xtar(k)在各个采样时刻所对应的状态空间分区号。可知在0.25 s和0.4 s参考电流发生阶跃变化的时刻，代价函数值迅速增大，随着反馈电流快速的跟踪上参考值后而减少到0，验证了模型预测控制是通过惩罚状态的偏差而使得代价函数值最小继而获得最优控制输入；在0.25 s时刻的电流动态过程由于状态向量的多个参数变化范围较大，因此激活了多个状态空间分区，说明EMPC控制器这次较大的电流阶跃过程中采用了不同的状态反馈控制规律，以便能更快地跟踪参考值的变化。

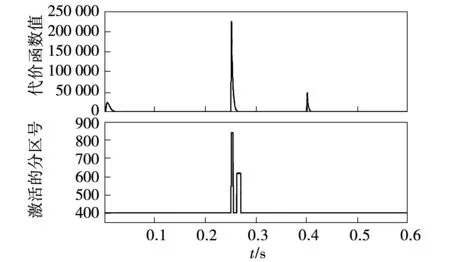
图5 EMPC控制器的代价函数和激活区域的仿真结果Fig.5 Simulation results of the cost function value and the activated region number

图6为控制输出即d、q轴电压波形，可见稳态时波动很小，在0.25 s电流阶跃时，电压矢量幅值Us达到最大值191 V，电压约束条件触发，EMPC电流控制器在动态调节过程中能充分利用SVPWM线性调制的最大输出能力以实现最快的电流动态响应，控制电压波形变化规律简单，说明是以代价函数所定义的最优方式实现控制目标。

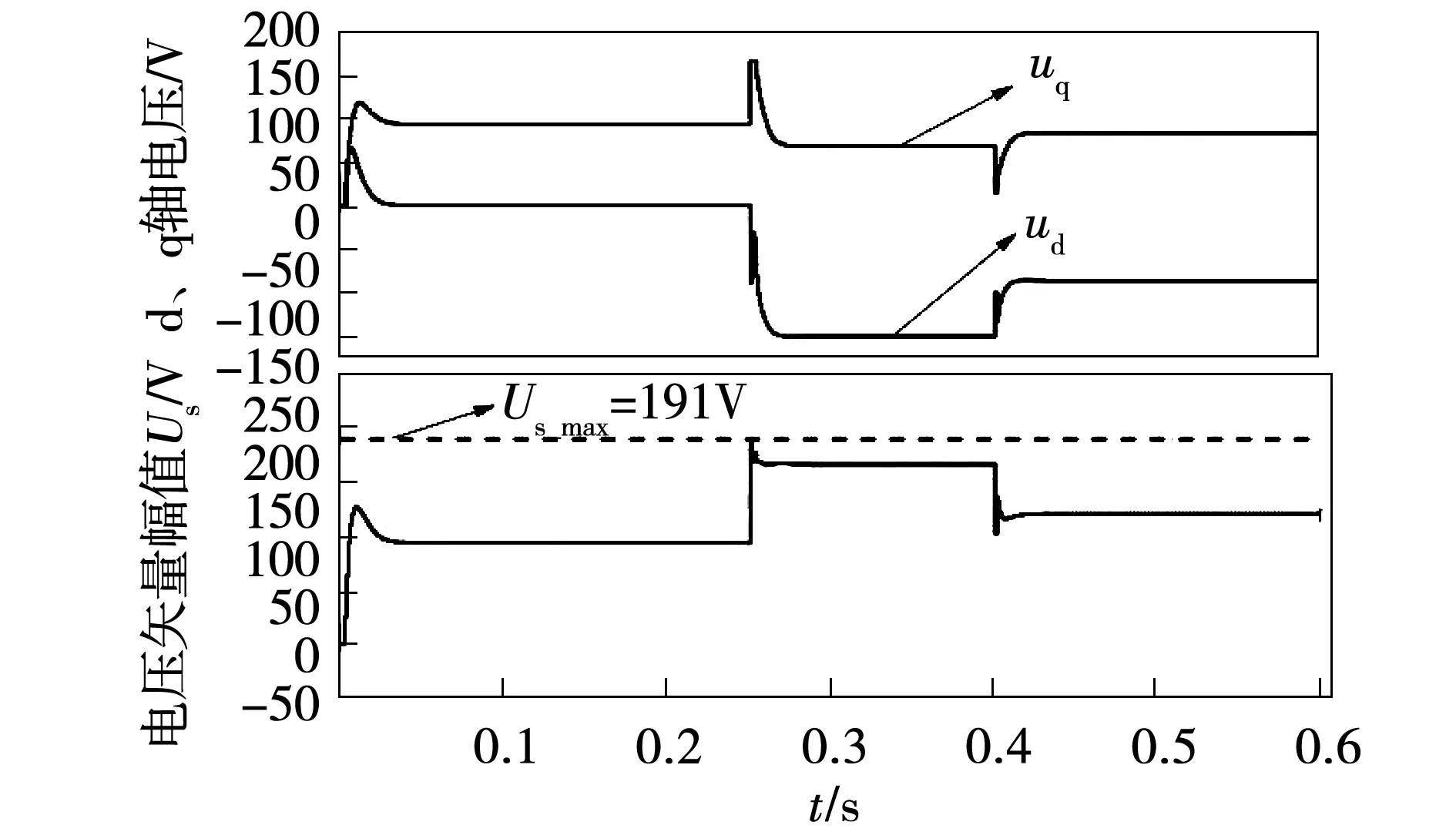
图6 d、q轴电压波形仿真结果Fig.6 Simulation results of d-and q-axis voltages

1.6 实验结果分析

实验所用的电机参数与表1一致，搭建了以英飞凌的高性能处理器Tricore TC1782为核心的逆变器平台进行了实验验证，采用SVPWM调制，逆变器开关频率10 kHz。实验过程如下：测功机作为负载，拖动被测电机到额定转速4 500 r/min(ωe=471 rad/s)，0.42 s时刻给定电流id=-284 A,iq=289 A。0.65 s时刻阶跃到id=-87 A,iq=146 A。图7展示了以表1中的电感值为辨识算法初始值的d、q轴电感参数在线辨识结果，可见0.42 s这次电流阶跃，导致辨识到的q轴电感值从初始值0.282 mH减少到0.271 mH，d轴0.067 mH减少到0.061 mH，这是因为d轴电感在永磁体强磁场下通常已经处于磁饱和状态，所以交叉饱和效应对其影响不大，但对q轴电感有显著影响。

图7 d、q轴电感辨识结果Fig.7 Identification results of d- and q-axis inductance

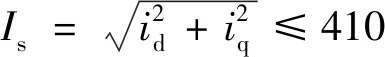
图8 d、q轴电流阶跃响应实验结果Fig.8 Experimental results of d-and q-axis currents step response

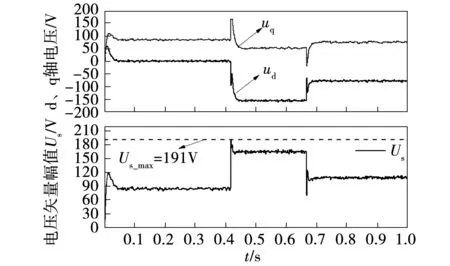
图9 d、q轴电压波形Fig.9 Experimental results of d-and q-axis voltages

图10 EMPC控制器激活区域和代价函数实验结果Fig.10 Experimental results of the activated region number and cost function value

4 结 论

本文提出一种基于带遗忘因子的RLS的电感参数在线辨识，结合模型预测控制的电流控制器的设计方法，通过将辨识结果应用于IPMSM动态模型中的转速相关项的计算，从而得到被控对象的线性状态空间方程，依据此线性模型设计了模型预测电流控制算法。同时应用显示模型预测控制技术，离线求得最优状态反馈，解决了在线计算量大的问题。本文所提出的电感参数辨识算法能够准确的辨识出电感参数，具有计算量小、收敛快的特点，与显示模型预测控制算法构成的闭环系统可以实现高性能电流动态响应；采用在线辨识参数的方式提高了模型预测控制策略对参数变化的鲁棒性，获得了高动态电流响应，仿真和实验均证明了所提方法有效性和实用性，可以成功地应用于内置式永磁同步电机的电流控制中。