电动汽车用PMSM带滤波补偿三阶滑模自抗扰控制

王晓远，刘铭鑫，陈学永,2，李小宁

(1.天津大学 电气自动化与信息工程学院，天津 300072；2.天津内燃机研究所，天津 300072)

0 引 言

随着全球气候问题日益加剧，低污染、高效的电动汽车深受关注，逐渐成为研究的热点问题。内置式永磁同步电机因其电磁转矩大、调速范围宽等优点[1-3]，广泛地应用于电动汽车驱动电机领域中。在电动汽车中常采用最大转矩电流比(maximum torque per ampere,MTPA)控制的永磁同步电机(permanent magnet synchronous motor, PMSM)矢量控制方法。相比较于id=0控制方法，MTPA能够充分利用电机的磁阻转矩，从而实现以较小电流得到相同转矩的目的，更符合电动汽车对于大转矩的要求[4]。

然而，电动汽车具有运行工况复杂、干扰大等特点，因此对驱动电机的控制系统有着更高的要求。传统应用的PI控制器无法满足PMSM控制系统对高给定跟踪性能与强抗扰能力的要求。伴随着非线性控制理论的发展，模型预测控制(model predictive control, MPC)[5-8]、模型参考自适应控制(model reference adaptive control, MRAC)[9-10]、滑模控制(sliding mode control, SMC)[11-14]等开始被用来替代PI控制用以驱动永磁同步电机。其中，滑模控制是一种变结构控制，滑模控制函数的开关特性将系统的工作点限制在滑动模态上，并进一步运动到稳定点，具有响应速度快、抗扰能力强等优点。但滑模控制通常是使用较大的开关增益来实现对干扰的快速控制，这将会导致控制系统所不期望的抖振现象的发生。

针对这一问题，一些学者致力于设计新型滑模趋近律与开关函数。文献[15]设计了一种基于新型趋近律和高阶快速终端滑模观测器的新型滑模控制方法，有效地减小了负载扰动引起的速度波动；文献[16]提出了一种改进型变指数趋近律的滑模控制器，在一定程度上抑制了抖振；文献[17]将一种新型的分数阶滑模控制器用于永磁同步电机转速环控制，具有较好的鲁棒性。但这一类改进方法，当永磁同步电机运行于低速受到干扰时，仍存在着抖振问题。另有一些学者将滑模控制与干扰观测器相结合，利用干扰观测器等效估计控制系统内部的扰动，并利用这一估计的扰动对滑模控制器进行补偿，从而减轻干扰变化对滑模控制器性能的影响[18-19]。然而，干扰观测器的设计依赖于精确的控制模型， MTPA控制策略的数学模型较为复杂，计算量过大。

自抗扰控制[20]因其优越的抗扰性能以及不依赖被控对象精确数学模型的优点受到国内外学者的广泛关注。其主要思想为将控制系统内部不可建模的部分与外界环境的未知干扰当作系统的总干扰，由扩张状态观测器观测出来，进行补偿以消除干扰的影响[21]。文献[22]将自抗扰控制与滑模控制结合在了一起，无需建立精确的永磁同步电机数学模型，具有良好抗扰性能的同时减小了滑模控制所带来的抖振影响，但其仅仅将改进技术应用于电流环，转速环仍采用传统的PI控制。文献[23]将滑模自抗扰控制融入转速-电流控制器的设计中，并将已知扰动与未知扰动分离以减小计算量，具有调速范围宽、抗扰能力强的优点。但是在电动汽车用PMSM控制系统中，通常会使用低通滤波器滤除由系统内外部产生的干扰在转速环中产生的噪声，将会导致转速反馈存在相位延迟的问题。

论文采用滑模控制思想提高电动汽车用永磁同步电机控制性能，将自抗扰控制引入其中，利用低通滤波器数学模型实时补偿转速反馈信号，提出电动汽车用永磁同步电机带滤波补偿三阶滑模自抗扰控制(filtered sliding mode active disturbance rejection control，FSM-ADRC)。为了削弱滑模控制器的抖振，避免使用最大转矩电流比控制策略所带来的计算模型复杂的问题，提高控制系统给定跟踪能力与抗扰性能，对未知扰动的实时估计补偿，提高负载扰动以及电机参数失配等情况下的转速响应能力与抗扰性能。

1 二阶滑模控制

1.1 PMSM数学模型

本文所研究的被控对象为内置式永磁同步电机，使用最大转矩电流比控制策略。内置式永磁同步电磁转矩表达式为

(1)

式中：p为电机极对数；ψf为转子永磁体磁链；iq为q轴电流；id为d轴电流；Ld、Lq分别为d、q轴电感。

PMSM运动状态方程与dq轴电压方程为:

(2)

式中：TL为负载转矩；J为转动惯量；ω为电机角速度；B为摩擦因数；ud、uq分别为d轴与q轴电压；R为定子电阻。

1.2 PMSM二阶滑模控制器动态模型

结合PMSM运动状态方程与电压方程，考虑未知扰动的影响。选取角速度ω为状态变量x1，则转速环滑模控制器状态方程可以设计为:

(3)

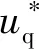
f为包含系统内部扰动与外部扰动的总扰动。将系统内部扰动fn定义为

(4)

其中：

(5)

将永磁同步电机磁阻转矩放入总扰动中进行估计，可以降低MTPA控制策略的模型计算复杂度，节约时间成本。

PMSM转速环控制器总扰动为

(6)

式中：ΔR为定子电阻变化量；Δψf为永磁体磁链变化量；ΔLd为d轴电感变化量。

定义转速环滑模面误差为

δ=ω*-ω。

(7)

式中ω*为电机给定角速度。

设计二阶滑模控制器的滑模面为

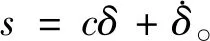
(8)

式中c>0为二阶滑模控制器滑模面系数。

将系统总扰动考虑在内，设计控制器趋近律为

(9)

式中：sgn(·)为开关函数；η>0为开关函数增益。

此时，二阶滑模控制器输出为

(10)

1.3 二阶滑模控制器收敛性分析

使用Lyapunov稳定性验证二阶滑模控制器的稳定性，表达式为

(11)

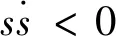
η>|f|。

(12)

2 带滤波补偿三阶滑模自抗扰控制

由于未知扰动的不确定性，若二阶滑模控制器保持稳定，则需要较大的η。这将导致滑模控制器抖振加剧，不利于控制系统稳定。而且，PMSM控制系统在使用低通滤波器滤除谐波等高频噪声干扰时会带来反馈信号相位偏移，进而导致控制系统准确性降低。针对以上问题，本文提出一种带滤波补偿三阶滑模自抗扰控制器，在二阶滑模控制器的基础上，引入自抗扰控制的思想。根据低通滤波器与PMSM数学模型构建跟踪微分器，根据滑模面函数构建非线性状态误差反馈控制律，另构建改进型扩张状态观测器进行总扰动估计，提高PMSM系统控制精度。

2.1 FSM-ADRC控制器的构建

1)跟踪微分器。

低通滤波器数学模型为

(13)

式中：ωf为滤波后电机角速度；Tω为低通滤波器时间常数。

基于低通滤波器数学模型与PMSM二阶滑模控制器方程，令状态变量xq1=ωf，构建的带滤波补偿三阶滑模自抗扰控制器跟踪微分器为：

(14)

式中：K=kt/Tω为跟踪微分器系数；FSM-ADRC控制器已知扰动fyq=-K(Riq+ωfLdid+ωfψf)。

FSM-ADRC控制器总扰动为

(15)

内部扰动为

(16)

其中：

(17)

2)非线性状态误差反馈控制律。

基于滑模控制器模型构建非线性状态误差反馈控制律，定义FSM-ADRC滑模面误差为

δq=ω*-ωf。

(18)

基于跟踪微分器模型设计FSM-ADRC的滑模面为

(19)

式中：cq1与cq2为FSM-ADRC滑模面系数，且cq1>0，cq2>0。

为使控制器可以收敛于稳定状态，设计滑模面趋近律为

(20)

式中ηq> 0为FSM-ADRC开关增益。

此时，FSM-ADRC输出为

(21)

与二阶滑模控制器相同，为使系统收敛，FSM-ADRC也需要较大的开关增益。

为解决此问题，本文使用改进型扩张状态观测器进行扰动估计，补偿到控制器输出中，极大地减小滑模控制器开关增益。

3)改进型扩张状态观测器的构建。

(22)

三只松鼠股份有限公司2012年12月成立于安徽芜湖，主要从事于坚果类、茶类和休闲零食类等食品的新兴互联网企业，整个业务流程涉及产品的研发、分装和销售，并在淘宝天猫商城上线65天后就成为了中国坚果类电商食品第一名，是中国第一家纯互联网食品品牌企业。三只松鼠的成功有其独特之处，通过对其创业方式、营销手段和企业文化等方面的探讨研究，为其他同类型企业的发展提供借鉴。

(23)

式中rq>0为转速环改进型扩张状态观测器扰动增益。

另，将FSM-ADRC滑模面趋近律替换为

(24)

此时，控制器的输出为

ηqsgn(sq)]/K。

(25)

2.2 FSM-ADRC控制器稳定性分析

为验证FSM-ADRC收敛性能，所构建的Lyapunov函数为

(26)

则

(27)

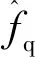
(28)

则

(29)

此时，只要ηq选取任意大于0的值均可使控制系统稳定，极大地削弱了滑模控制器的抖振现象。三阶FSM-ADRC控制器结构框图如图1所示。

图1 三阶FSM-ADRC控制器结构框图Fig.1 Structure block diagram of third order FSM-ADRC controller

2.3 d轴电流环控制器的构建

在d轴电流环中，采用一阶滑模自抗扰控制器(sliding mode active disturbance rejection control， SM-ADRC)。

1)跟踪微分器。

令状态变量xd1=id，基于d轴电压方程构建的d轴电流环跟踪微分器为

(30)

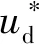
已知扰动fyd为

(31)

未知扰动fd为

(32)

2)非线性状态误差反馈控制律。

定义d轴电流环滑模面误差为

(33)

设计d轴电流环控制器滑模面为

(34)

式中cd>0为d轴电流环滑模面系数。

设计d轴电流环滑模面趋近律为

(35)

式中ηd>0为d轴电流环滑模面开关增益。

此时，d轴电流环控制器输出为

(36)

式中

(37)

3)改进型扩张状态观测器的构建。

将d轴电流环改进型扩张状态观测器的误差定义为

(38)

改进型d轴扩张状态观测器方程为：

(39)

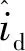
将式(35)改为

(40)

改进后的SM-ADRC控制器输出为

(41)

一阶SM-ADRC控制器结构框图如图2所示。

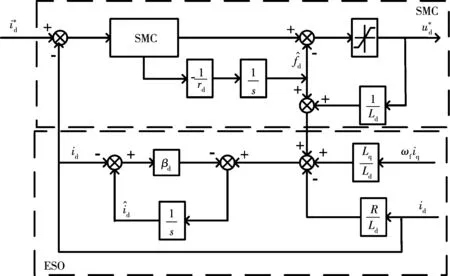
图2 一阶SM-ADRC控制器结构框图Fig.2 Structure block diagram of first order SM-ADRC controller

3 仿真分析与实验验证

电动汽车用内置式永磁同步电机带滤波补偿三阶滑模自抗扰控制系统结构图如图3所示。为验证本文所提控制方法的有效性，针对永磁同步电机控制系统分别做了仿真与实验验证。仿真与实验所用的永磁同步电机参数如表1所示。

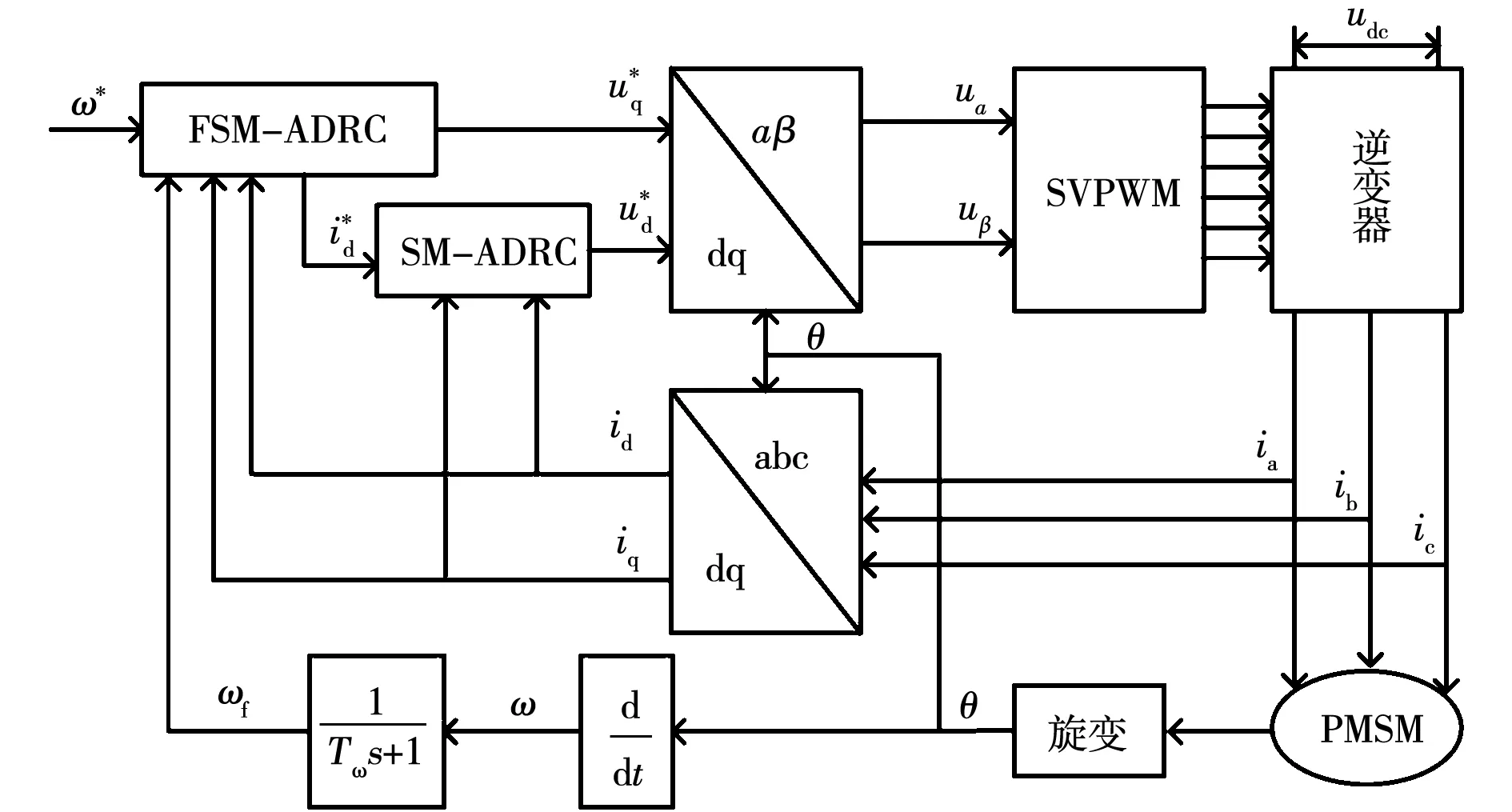
图3 FSM-ADRC控制系统结构框图Fig.3 Structure block diagram of FSM-ADRC control system

表1 仿真与实验用PMSM参数Table 1 PMSM paraments used in simulation and experiment

3.1 仿真分析

为测试FSM-ADRC控制系统抗负载扰动能力，设置控制系统给定转速为1 200 r/min，负载转矩由最初的空载状态到0.4 s时突增至50 N·m，上述三种控制策略抗负载扰动性能与给定跟踪误差对比如图4所示。

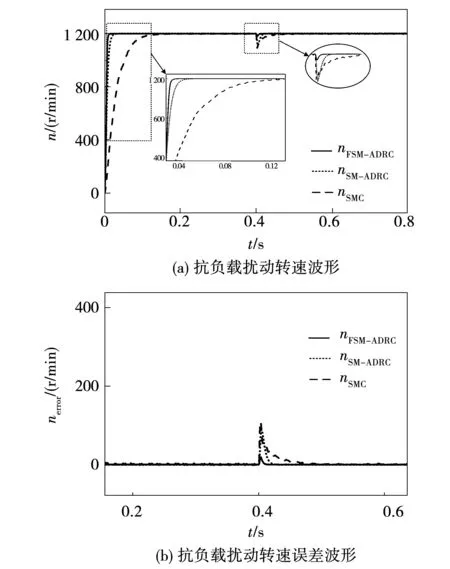
图4 抗负载扰动转速仿真波形Fig.4 Anti load disturbance speed simulation waveform

三种控制方法在负载扰动时性能对比如表2所示。可以看到，FSM-ADRC控制方法相较于SMC与SM-ADRC控制方法更快地到达给定转速1 200 r/min，无抖振现象，且在50 N·m的负载扰动时转速最大跌落为30 r/min，误差仅为2.5%。

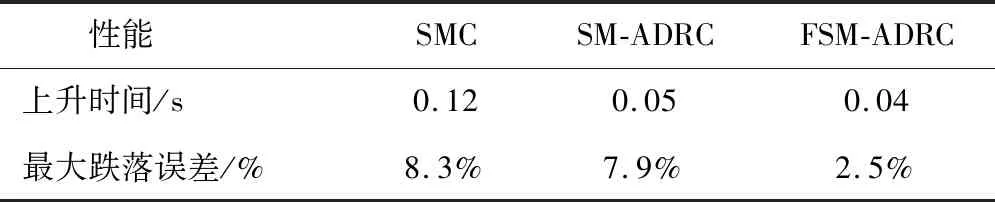
表2 三种控制方法在负载扰动时性能对比表Table 2 Performance comparison table of three control methods under load disturbance

为测试电动汽车用永磁同步电机FSM-ADRC控制器的给定跟踪能力，分别给予控制系统正弦与三角给定转速，对比滑模控制方法、滑模自抗扰控制方法以及本文所提出的带滤波补偿滑模自抗扰控制方法，得到三种控制方法的正弦给定与三角给定跟踪转速与误差波形分别如图5与图6所示。

图5 正弦给定转速仿真波形Fig.5 Sine given speed simulation waveform

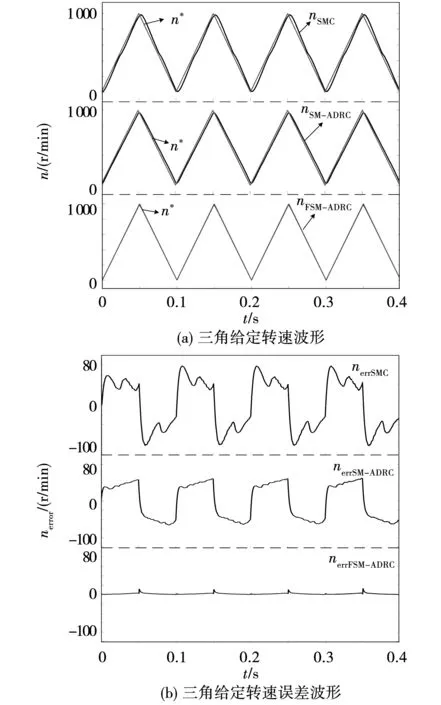
图6 三角给定转速仿真波形Fig.6 Triangle given speed simulation waveform

可以看到，跟踪正弦与三角给定时，FSM-ADRC方法由于进行了滤波补偿，相对于SMC与SM-ADRC控制方法具有更精准的给定跟踪能力，跟踪误差较小，几乎没有幅值衰减与相位偏移问题。正弦给定与三角给定相对于阶跃给定而言更加难以跟踪， 因此可以证明FSM-ADRC具有很好的跟踪精度，可以满足电动汽车对于实时准确跟踪的需求。

由于电动汽车在复杂工况下行驶易导致电机内部参数的变化，为测试FSM-ADRC控制方法对电机参数变化的敏感性，在参数失配情况下进行负载扰动实验。

图7为给定转速1 200 r/min、0.4 s突增50 N·m负载情况的参数失配时三种方法永磁同步电机抗负载扰动转速波形。三种方法在电机参数失配情况下性能对比如表3所示。

表3 三种控制方法参数失配负载扰动时性能对比表Table 3 Performance comparison of three control methods anti-load disturbance speed with motor parameter change

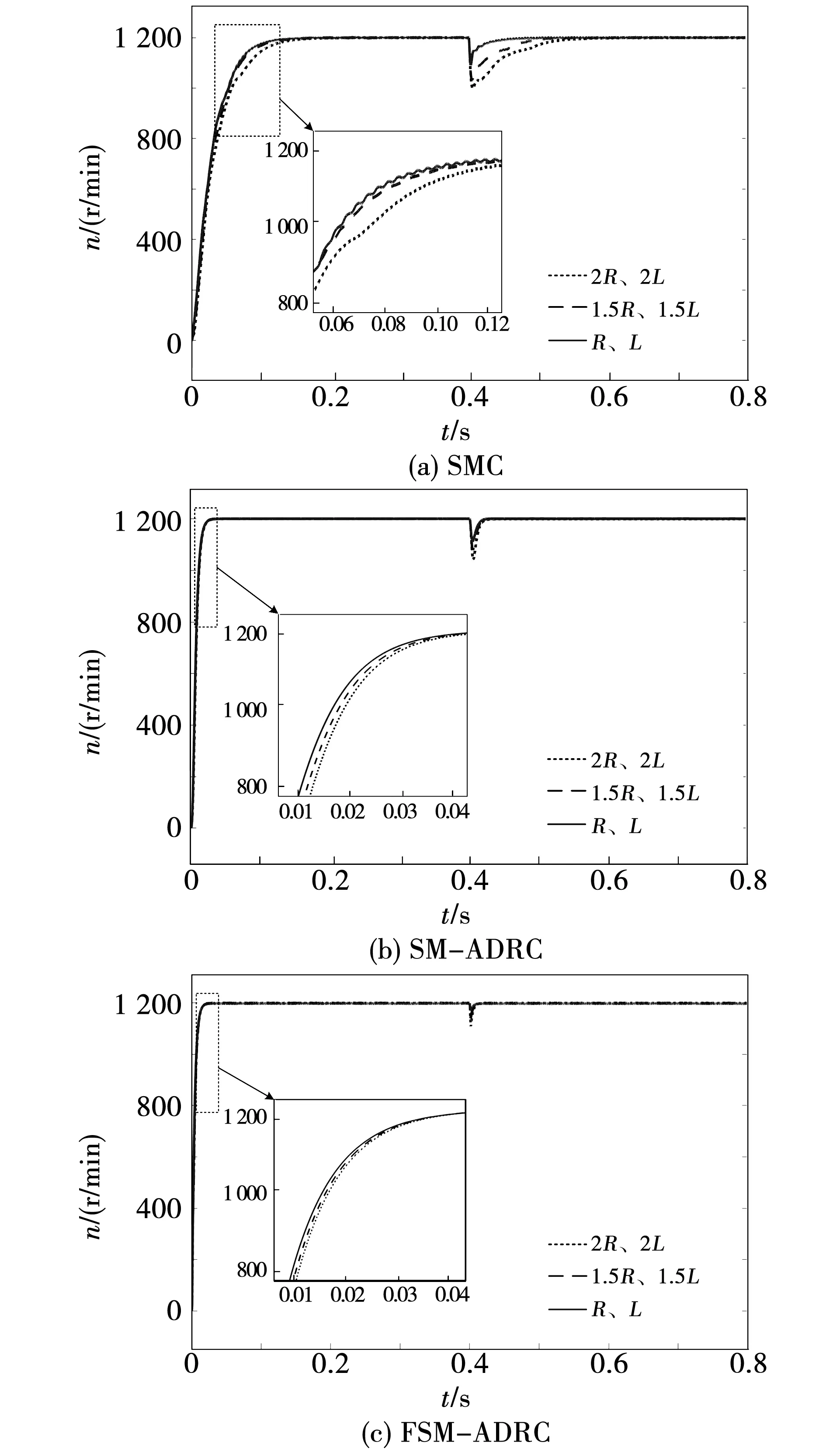
图7 三种方法电机参数失配抗负载扰动转速仿真波形Fig.7 Three methods anti-load disturbance speed with motor parameter change speed simulation waveform

与SMC与SM-ADRC控制方法相比，电机参数失配情况下，FSM-ADRC控制方法的转速上升时间基本未变，转速最大跌落误差虽略有增加，但相比较于SMC控制方法与SM-ADRC控制方法在电阻、电感值增加100%时，转速最大跌落误差分别增大11.5%与7.6%相比，FSM-ADRC控制方法仅增大3.8%，可以相对更加快速地回归稳定状态，对电机参数变化的敏感度较低。

图8为永磁同步电机参数失配时FSM-ADRC控制系统正弦与三角给定转速跟踪仿真波形。FSM-ADRC在参数变化前后均保持很强的给定跟踪能力，误差值很小。由此可见，FSM-ADRC永磁同步电机控制系统对参数变化的敏感性较低。

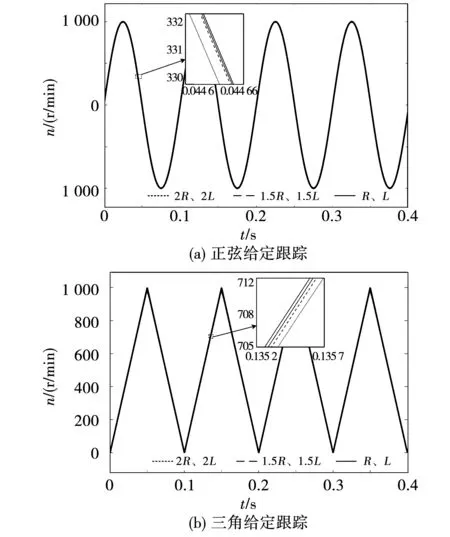
图8 正弦及三角给定转速仿真波形Fig.8 Sine and triangle given speed simulation waveform

仿真结果表明，本文所提的FSM-ADRC永磁同步电机控制系统具有良好的鲁棒性，相对于SMC与SM-ADRC具有更加良好的给定跟踪能力与抗负载扰动性能。

3.2 实验验证

为进一步验证所提方法，所用的实验平台如图9所示。

图9 实验平台Fig.9 Experimental platform

设定给定转速为1 100 r/min、空载启动，分别使用三种控制方法的永磁同步电机抗负载扰动转速实验波形如图10所示。可以看到，FSM-ADRC控制方法比SMC控制方法具有更加快速的动态响应能力。而且，相比较于其他两种控制方法，FSM-ADRC在负载突变时的转速波动更小，抗负载扰动能力更优。

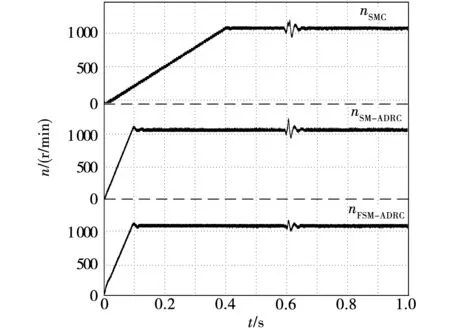
图10 抗负载扰动转速实验波形Fig.10 Anti load disturbance speed experimental waveform

为在实验中验证SMC、SM-ADRC与FSM-ADRC控制器在电机参数失配时的电机敏感性，分别设置三种控制器中的电阻与电感量为实际值的两倍。由图11所示，当电机参数失配时SMC与SM-ADRC控制器抗扰性能均有明显降低，其中SMC控制器电机参数失配时转速最大跌落误差与原来相比增加了12.8%，SM-ADRC增加了8.4%。而FSM-ADRC控制器性能几乎没有变化，与电机未失配时相比仅增加了4%。由此可见，FSM-ADRC永磁同步电机控制系统对电机参数变化不敏感，可以适用于多种复杂工况。

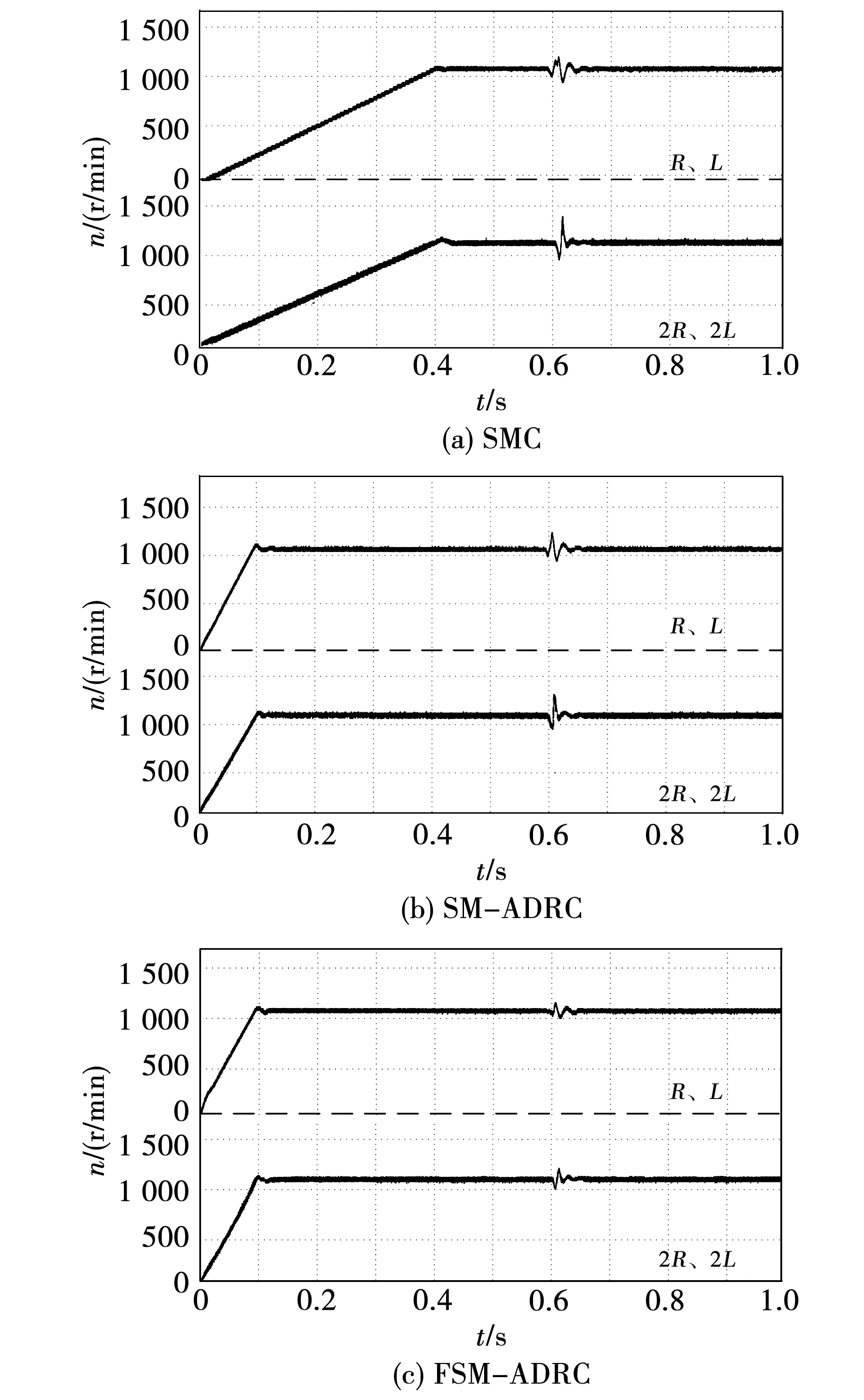
图11 电机参数失配三种方法抗负载扰动转速实验波形Fig.11 Three methods anti-load disturbance speed with motor parameter change speed experimental waveform

实验结果表明，本文所提的带滤波补偿滑模自抗扰控制方法的抗扰性能强、参数敏感性低，可以显著提升电动汽车用永磁同步电机控制系统性能。

4 结 论

针对电动汽车用永磁同步电机存在的复杂工况下控制系统抗扰性能降低以及跟踪能力变差的问题，本文提出了永磁同步电机带滤波补偿三阶滑模自抗扰控制方法，经过补偿后，滑模控制器的抖振问题有了明显改善，控制系统的抗扰性能显著提升。仿真与实验表明，与采用SMC与SM-ADRC的永磁同步电机控制系统相比，采用FSM-ADRC的控制系统具有更良好的鲁棒性，适用于对精度要求更高的控制领域。