基于特征值灵敏度的共模-差模电压控制SIDO Buck变换器稳定性分析
2021-12-29皇金锋谢锋李慧慧
皇金锋,谢锋,李慧慧
(陕西理工大学 电气工程学院,汉中 723001)
0 引 言
单电感双输出(single-inductor dual-output,SIDO)Buck变换器用一个电感实现双路输出[1],减小了变换器体积,节约了制作成本,具有广阔的应用前景[2-3],可作为便携式移动设备的供电电源拓扑,成为近年来国内外研究热点[4-10]。
工作于连续导电模式(continuous conduction mode,CCM)SIDO Buck变换器输出端存在交叉影响,严重影响了变换器的稳定性,针对SIDO Buck变换器的性能问题,国内外专家学者做了许多研究工作[11-14]。文献[11]建立了电压控制SIDO CCM Buck变换器的统一离散迭代映射模型,结果表明,电压控制SIDO CCM Buck变换器随支路开关管控制回路比例系数的减小或主开关管控制回路比例系数的增大而发生Hopf分岔。文献[12]采用状态空间平均法,分析了控制参数变化时电压控制SIDO Buck变换器的稳定性,研究结果表明,电压控制参数具有稳定上界或下界。文献[13]建立了峰值电流模式(peak current mode, PCM)SIDO Buck变换器的统一离散迭代模型,研究结果表明,变换器的稳定性与参考电流、初始电感电流和输入电压的变化密切相关。文献[14]提出了一种电容电流纹波(capacitor current ripple,CCR)控制技术,通过特征值分析了负载变化对CCR SIDO CCM Buck变换器稳定性的影响,研究结果表明,提出的CCR控制SIDO CCM Buck变换器显著降低了交叉影响并改善了瞬态性能。以上研究对提高SIDO Buck变换器的稳定性具有实际意义,但是现有文献关于控制参数变化对稳定性的影响趋势及程度还未研究。
相比传统的独立电压控制,共模-差模电压[15](common-mode voltage and differential-mode voltage,CMV-DMV)控制策略在不增加电路复杂程度的基础上能够有效降低变换器的交叉影响,然而该控制策略还未应用于SIDO Buck变换器,且关于CMV- DMV控制CCM SIDO Buck变换器的稳定性研究还未见报道。目前关于稳定性研究主要分为线性方法和离散方法,线性方法主要依据系统的传递函数,高阶系统的传递函数具有较大的近似性,这导致分析误差较大。离散方法一般适用于低阶系统,高阶系统的离散模型十分复杂且求取困难。SIDO Buck变换器具有较高的阶数,同时有更多的电路参数和控制参数,对该系统的稳定性分析变得更加困难和复杂,故而寻求更为简便的方法显得尤为重要。状态空间平均方程可表征变换器的线性特征,基于状态空间平均方程的雅克比矩阵和劳斯-赫尔维茨判据可以得到系统稳定的变换器参数和控制参数范围[16-17],然而该方法在获得稳定参数范围后无法进一步优化参数从而提高系统的稳定性。应用灵敏度理论[19],可定性定量地分析系统各个参数对特征值的影响趋势及影响程度,从而达到改善系统稳定性的目的,因此利用状态空间平均模型并结合灵敏度理论能够较为全面的对系统的稳定性进行分析。
本文以CMV-DMV控制CCM SIDO Buck变换器为研究对象,建立了系统的状态空间方程,结合雅克比矩阵和劳斯-赫尔维茨判据得到了变换器控制参数的稳定范围,利用变换器的工作模式及输出纹波电压等约束条件得到了变换器的主电路参数范围,在此基础上应用灵敏度分析了控制参数变化对系统稳定性的影响。本文研究所得结论对CMV-DMV控制CCM SIDO Buck变换器控制器设计具有参考意义。
1 稳定性分析
CMV-DMV控制CCM SIDO Buck变换器的电路结构如图1所示,将两路输出电压的和与共模参考电压进行比较生成脉冲信号Di作用于输入开关管Qi,同时将两路输出电压的差与差模参考电压比较生成脉冲信号Da和Db作用于支路开关管Qa和Qb。
图1中,UCref=Urefa+Urefb为共模参考电压,UDref=Urefb-Urefa为差模参考电压,Um为锯齿波的幅值。
为得到CMV-DMV控制CCM SIDO Buck变换器控制参数的稳定范围,需对变换器的稳定性进行分析,系统调节器采用比例积分,其传递函数为:
(1)
结合图1,由比例积分控制原理可知,变换器的瞬时占空比可表示为:
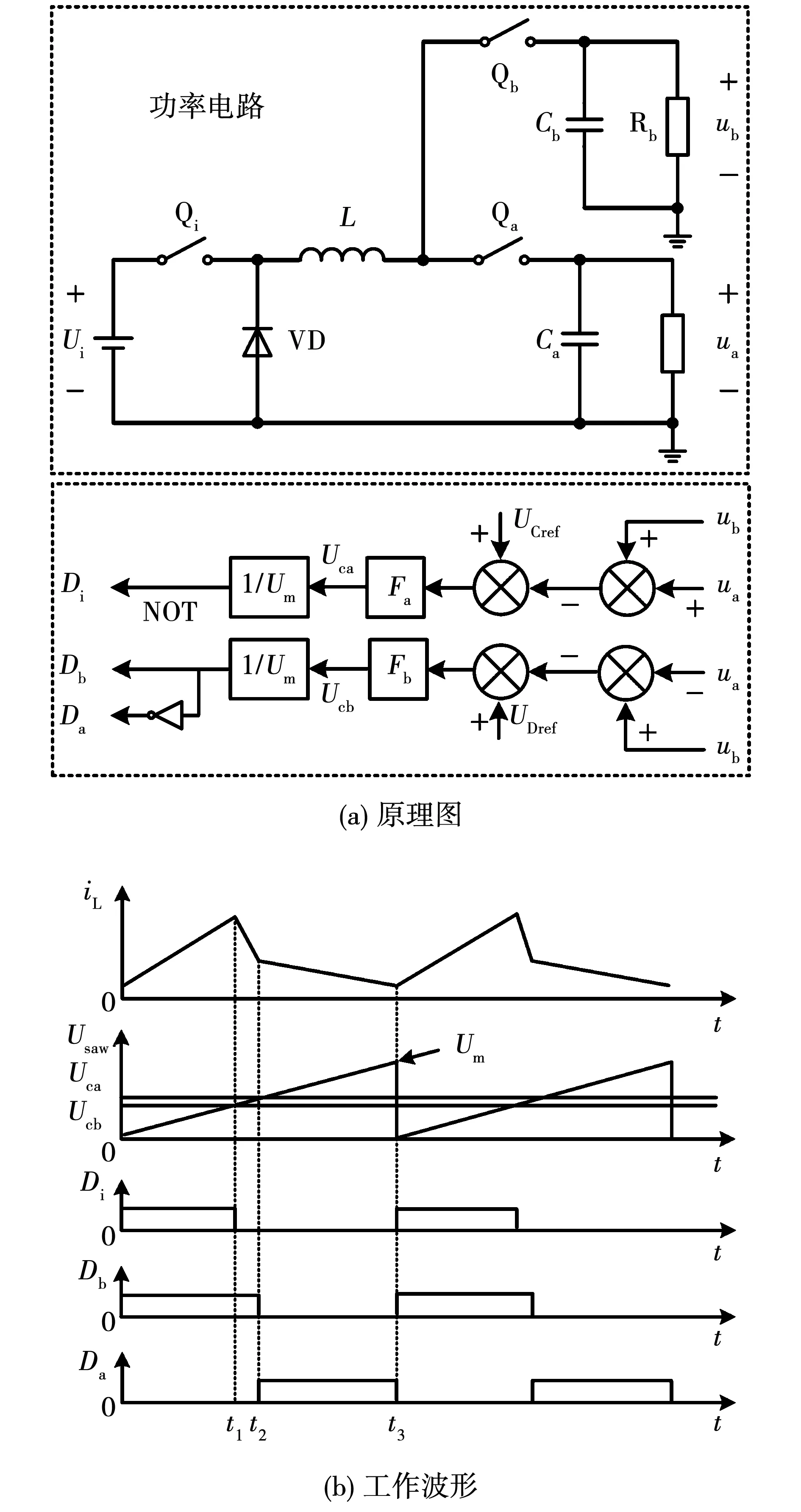
图1 共模-差模控制CCM SIDO Buck变换器Fig.1 Common mode-differential mode control CCM SIDO Buckconverter
(2)
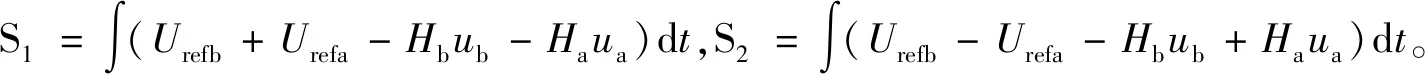
根据CCM SIDO Buck变换器的工作原理,结合状态空间平均法[16-17],可得闭环系统的状态空间平均模型为:
(3)
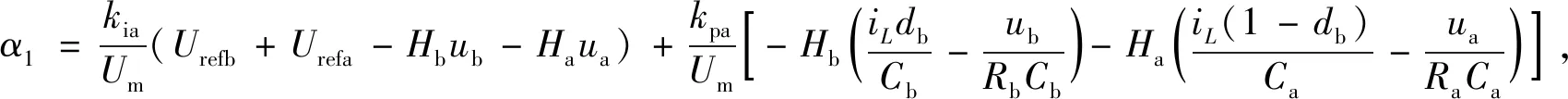
根据Floquet理论[18],结合式(3)可得系统的雅克比矩阵∂x ˙/∂x为:
(4)
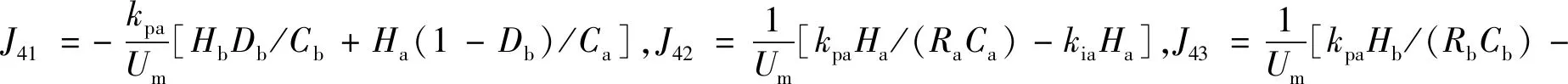
根据式(4)可以得到系统的特征方程:
|λI-J|=0。
(5)
将式(4)代入式(5)可得:
s5+as4+bs3+cs2+ds+e=0。
(6)
式(6)中a、b、c、d和e均为特征方程的系数,由劳斯-赫尔维茨判据即可得到变换器稳定的条件如式(7)所示。

(7)
式中,β=(ad-e)/a。
式(7)给出使得系统稳定的参数范围,若参数(例如控制参数)满足式(7)相关条件,则系统可工作在稳定状态。但是,满足符合条件的参数并不唯一,而是存在多组参数,在这多组参数中哪组参数更有利于提高系统的稳定不能直接得出结论,下面将应用灵敏度理论对稳定性进一步分析。
2 控制参数特征值灵敏度分析
2.1 系统特征值
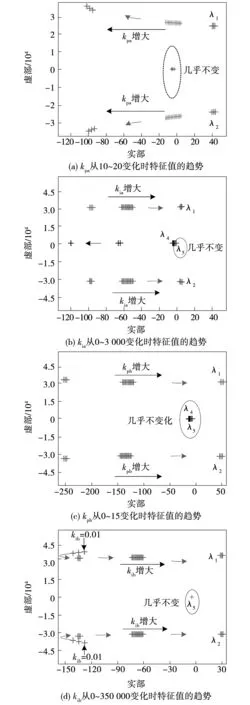
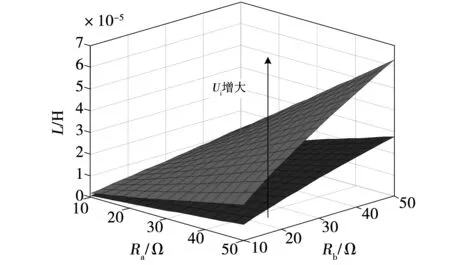
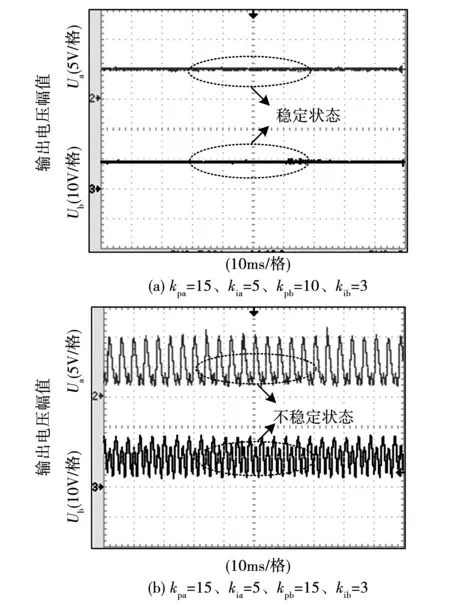
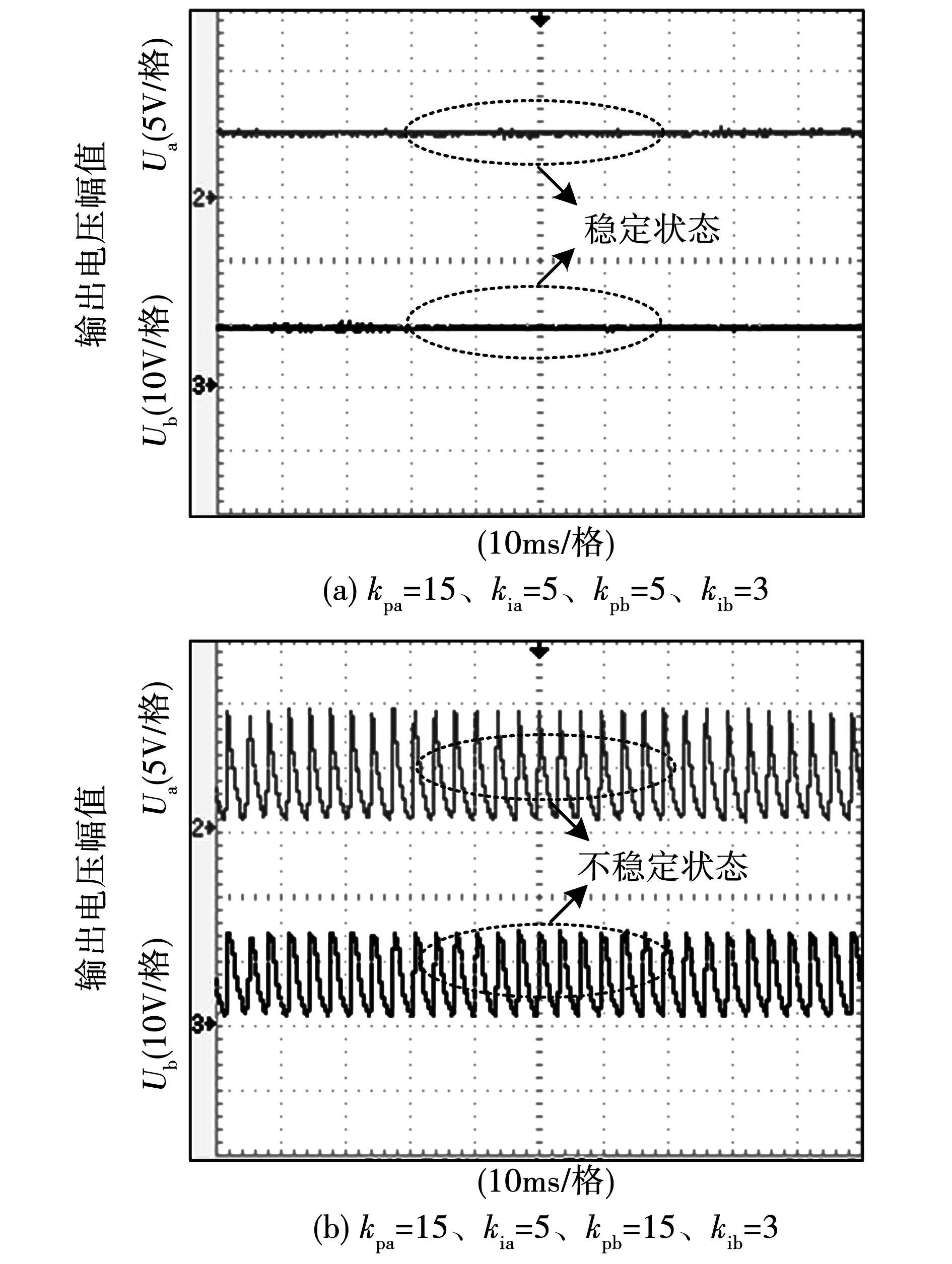
为了方便分析,现给出一组CMV-DMV控制CCM SIDO Buck变换器的参数:电感L=568 μH,电容Ca=161 μF、Cb=90 μF,输入电压Ui=20 V,负载Ra=20 Ω,Rb=20 Ω。根据式(7)可以得到控制参数的取值范围:当kpa=15、kia=5、kib=3时,kpb的取值范围为0.85 表1 系统特征值Table 1 System characteristic value 由表1可知,系统特征值的实部是负值,表明系统在平衡点处是稳定的。其中λ1,2是一对共轭复根,它的实部变化表征了系统的稳定程度,虚部变化表征了系统的阻尼程度及振荡频率的变化情况;λ4最靠近零轴,最有可能越过零轴使得系统不稳定,因此需要着重对λ1,2和λ4进行分析。 特征值灵敏度可定量表达出参数改变对系统影响的程度和趋势,从而为提高系统的稳定性提供理论指导。系统特征值λi对系统参数Kj的灵敏度[19]为: (8) 将以上变换器参数代入式(8)即可得特征值对控制参数的灵敏度,如表2所示。 表2 特征值对控制参数的灵敏度Table 2 Sensitivity of eigenvalues to control parameters 分析表2可知,λ1,2对控制参数的特征值灵敏度为复数,复数实部的绝对值大小反映了参数变化对系统稳定性的影响程度,并且当灵敏度的实部大于零时,减小该参数有利于提高系统的稳定性;当灵敏度的实部小于零时,增大该参数有利于提高系统的稳定性。结合表2,改变系统控制参数kpa、kia、kpb和kib的取值,即可得系统主要特征值的变化趋势,如图2所示。 由图2(a)可以看出,当kpa在[10,20]范围内变化时,系统的特征值从复平面的右半部分向左半部分移动,在kpa≥11.50时,共轭复根λ1,2的实部由正变负,且呈现虚部逐渐增大的变化特点;λ4、λ5为负实根并且靠近零点,最终稳定在-0.30,这表明kpa具有稳定下界。由图2(b)可以看出,当kia在[0,3 000]范围内变化时,系统的特征值从复平面的左半部分向右半部分移动,在kia≥2 865.0时,共轭复根λ1,2的实部由负变正,且呈现虚部基本保持不变的特点;λ4为负实根且从靠近零点的位置逐渐向左移动;λ5为负实根并且靠近零点,最终稳定在-0.29。由图2(c)可以看出,当kpb在[0,15]范围内变化时,共轭复根λ1,2的变化趋势同图2(b);在kpb≥12.50时,共轭复根λ1,2的实部由负变正,且呈现虚部逐渐减小的变化特点;特征根λ4、λ5的变化趋势同图2(a)。由图2(d)可以看出,当kib在[0,350 000]范围内变化时,共轭复根λ1,2的负实部先向左移动再向右移动;在kib≥331 000.0时,共轭复根λ1,2的实部由负变正,且呈现虚部逐渐减小的变化特点;特征根λ4、λ5的变化趋势同图2(a)。以上分析结果表明kpb、kia、kib具有稳定上界。 图2 控制参数变化时特征值的变化趋势Fig.2 Change trend of the characteristic value when the control parameter changes SIDO Buck变换器不仅需要设计控制参数,同时要进行主电路参数设计。主电路的电感需要满足工作模式的约束;电容需满足输出纹波电压的约束,下面给出参数设计方法。 3.1.1 电感设计 根据文献[6]可知,SIDO Buck变换器临界电感LC的表达式为: (9) 结合式(9),图3给出了临界电感在一定输入电压和负载范围内的变化情况。 图3 临界电感随负载和输入电压的变化关系Fig.3 Critical inductance changes with load and input voltage 分析式(9)可知,临界电感LC与输入电压Ui和负载Ra、Rb有关,将式(9)对输入电压Ui和负载Ra、Rb求偏导可得: (10) 分析式(10)可知,临界电感LC随着输入电压Ui,负载Ra和Rb的增大而增大,因此要求变换器全动态范围工作于CCM时,取1.2倍裕量可得变换器的电感取值范围: (11) 此时,变换器全动态范围均能满足变换器的工作模式要求。 3.1.2 电容设计 根据文献[6]可知,SIDO Buck变换器工作于CCM时两条支路的输出纹波电压分别为: (12) 分析式(12)可以看出,此时变换器的输出纹波电压与负载Ra和Rb有关,将式(12)分别对Ra和Rb求偏导可得: (13) 因此,工作在一定输入电压和负载范围内的SIDO Buck变换器输出纹波电压最大值分别为: (14) 根据式(14)可知,若变换器规定的最大输出纹波电压为UPP-a和UPP-b,电容取1.2倍裕量,则满足规定输出纹波电压要求的电容取值为: (15) 为了验证理论分析的正确性,搭建了如图4所示的CMV-DMV控制CCM SIDO Buck变换器实验平台,变换器参数如表3所示。 表3 CCM SIDO Buck变换器电路参数Table 3 Circuit parameters of SIDO Buck converter 图4 实验平台Fig.4 Experiment platform 根据式(11)和式(15)可得到满足变换器工作模式和输出纹波电压要求的电感和电容取值分别为:L=568 μH,Ca=161 μF,Cb=90 μF。 首先在Ui=30 V,Ra=Rb=10 Ω的条件下,根据式(7)可得到系统稳定的控制参数范围:当kpa=15、kia=5、kib=3时kpb的取值范围为0 图5 Ui=30 V,Ra=Rb=10 Ω时系统稳定性实验结果Fig.5 Experimental results of system stability at Ui=30 V,Ra=Rb=10 Ω 分析图5(a)可知,当控制参数为kpa=15、kia=5、kpb=20、kib=3时,控制参数在稳定范围之内,变换器是稳定的。分析图5(b)可知,当控制参数取kpa=15、kia=5、kpb=35、kib=3时,kpb的取值大于稳定值,变换器处于不稳定的低频振荡状态。 其次在Ui=20 V,Ra=Rb=20 Ω的条件下,根据式(7)可得到系统稳定的控制参数范围:当kpa=15、kia=5、kib=3时kpb的取值范围为0.85 图6 Ui=20 V,Ra=Rb=20 Ω时系统稳定性实验结果Fig.6 Experimental results of system stability at Ui=20 V,Ra=Rb=20 Ω 分析图6(a)可知,当控制参数为kpa=15、kia=5、kpb=10、kib=3时,控制参数在稳定范围之内,变换器是稳定的。分析图6(b)可知,当控制参数取kpa=15、kia=5、kpb=15、kib=3时,kpb的取值大于稳定值,变换器处于不稳定的低频振荡状态。 最后在Ui=15 V,Ra=Rb=50 Ω的条件下,根据式(7)可得到系统稳定的控制参数范围:当kpa=15、kia=5、kib=3时kpb的取值范围为0 图7 Ui=15 V,Ra=Rb=50 Ω时系统稳定性实验结果Fig.7 Experimental results of system stability at Ui=15 V, Ra=Rb=50 Ω 分析图7(a)可知,当控制参数为kpa=15、kia=5、kpb=5、kib=3时,控制参数在稳定范围之内,变换器是稳定的。分析图7(b)可知,当控制参数取kpa=15、kia=5、kpb=15、kib=3时,kpb的取值大于稳定值,变换器处于不稳定的低频振荡状态。以上实验结果验证了理论分析的正确性。 本文建立了共模-差模控制CCM SIDO Buck变换器的状态空间平均模型,利用雅克比矩阵和劳斯-赫尔维茨判据得到了控制参数的稳定范围。同时应用灵敏度理论,分析了共模-差模电压控制CCM SIDO Buck变换器特征值灵敏度对系统的稳定性影响程度。理论分析和实验结果表明:支路a的比例系数kpa具有稳定下界,积分系数kia具有稳定上界和下界;同时支路b的比例系数kpb和积分系数kib均具有稳定上界和下界。基于系统的灵敏度,得到了主导特征值对系统稳定性的影响程度,可通过合理设计控制器参数来改善系统的稳定性:即增大kpa、减小kia、减小kpb、减小kib有利于提高系统的稳定性。本文研究所得结论对共模-差模电压控制CCM SIDO Buck变换器的控制器设计具有实际的参考意义。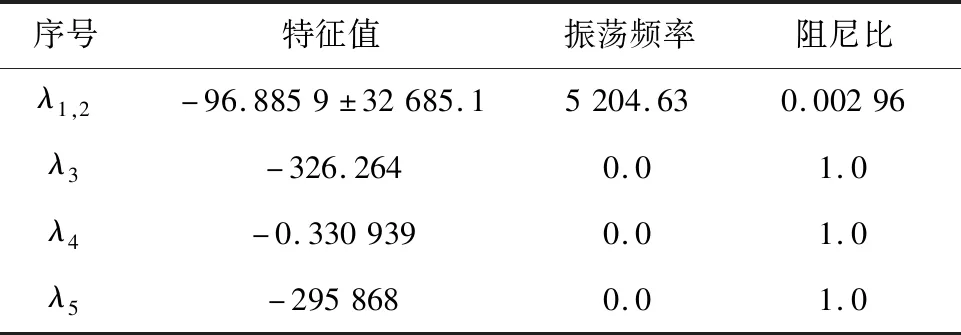
2.2 控制参数特征值灵敏度


3 实例分析
3.1 参数设计
3.2 实验验证



4 结 论
