Birkhoff系统稳定性的动力学控制1)
2020-08-11郭永新刘世兴梅凤翔
陈 菊 郭永新 刘世兴 梅凤翔
(北京理工大学宇航学院,北京 100081)
(辽宁大学物理学院,沈阳 110000)
引言
Birkhoff系统是一类应用广泛的约束力学系统.Birkhoff力学的研究已取得重要进展,如专著[1-4].在该力学系统下,关于稳定性的研究通常采用的方法是Lyapunov 函数法和一次近似法.特别对于自治和半自治Birkhoff系统而言,Birkhoff函数即为系统的积分.因此,如果Birkhoff函数在平衡邻域内是正定的,则平衡位置是稳定的.
力学系统的运动依赖于作用力以及所受的约束,因此既可以借助力来控制运动,也可以借助于约束来控制运动.前者称为动力学控制,后者称为运动学控制.本文讨论用动力学控制的方法研究Birkhoff系统和广义Birkhoff系统的平衡稳定性.虽然对于Birkhoff系统来说,其“作用力”并不明显,但是Birkhoff函数一般来说是具有能量意义的.因此,对Birkhoff系统和广义Birkhoff系统,均可借助Birkhoff函数中包含控制参数的方法来控制系统的运动.进一步地,Birkhoff系统亦可借助其附加项中所包含控制参数来控制系统的运动.这种用动力学函数来控制系统的运动,也可称为动力学控制.
针对以上构想,我们提出如下两个问题:(1)对于Birkhoff系统而言,Birkhoff函数B可依赖控制参数,若已知Birkhoff函数组Rµ(µ=1,2,···,2n),如何选取合适的控制参数使得零解稳定?(2)对广义Birkhoff系统,Birkhoff函数B或附加项Λν(ν=1,2,···,2n)可依赖控制参数,若已知Birkhoff函数组Rµ(µ=1,2,···,2n),如何选取合适的控制参数使得零解稳定?
1 系统的运动微分方程
Birkhoff方程为[1-3]

其中
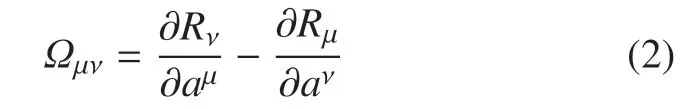
当det (Ωµν)≠0,可由方程(1)解出所有,有

其中

设方程(3)有零解
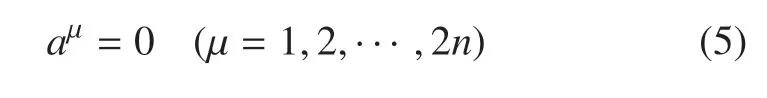
则平衡方程为

广义Birkhoff方程有形式[4-5]

其中

为附加项.设方程(7)有解

则平衡方程为

2 Birkhoff系统平衡稳定的控制
定理1假设给定Birkhoff函数B与Birkhoff函数组Rµ(µ=1,2,···,2n),其中B可含控制参数uρ(ρ=1,2,···r),则通过选取适当的控制参数可使系统的平衡是稳定的.
证明首先,选取B使之正定.其次,按方程求使之为负.由方程(3),求,有
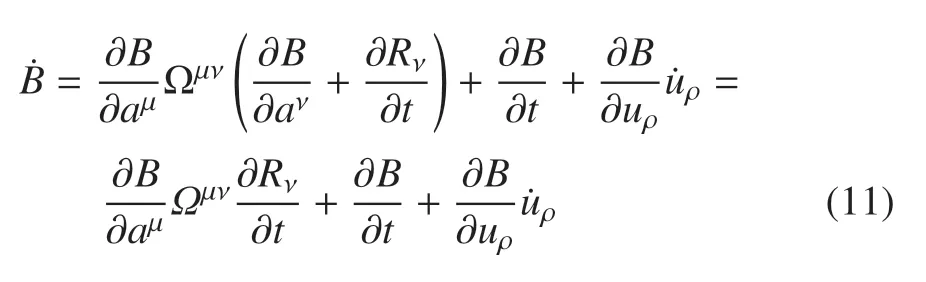
特别地,如果
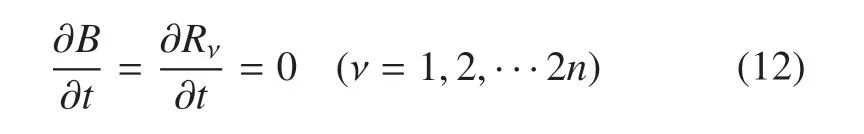
则有

如果适当控制参数uρ(ρ=1,2,···r)的选取使得<0,则平衡是稳定的.
3 广义Birkhoff系统平衡稳定的控制
定理2对广义Birkhoff系统平衡稳定的控制,可提出两类问题:
(1)对给定的Birkhoff函数B,Birkhoff函数组Rµ(µ=1,2,···,2n)和附加项Λν(ν=1,2,···,2n),如果B含控制参数uρ(ρ=1,2,···,r),则可选适当的控制参数使平衡是稳定的.
(2)对给定的Birkhoff函数,Birkhoff函数组和附加项,如Λν含控制参数,则可选适当的控制参数使平衡是稳定的.
证明首先选B为正定的.其次,求其导数.如果B含控制参数,则有
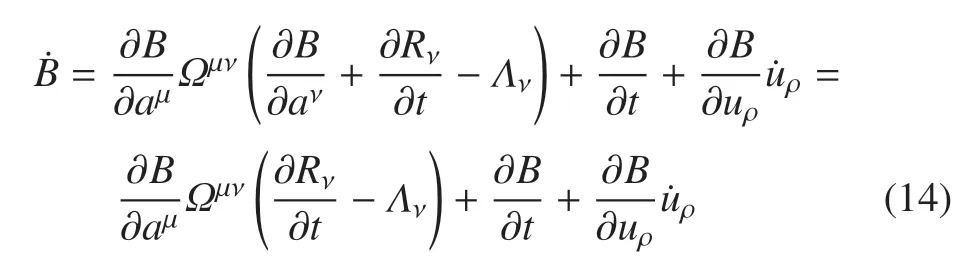
如果仅Λν(ν=1,2,···,2n)含有控制参数,则

由Lyapunov 定理可知,若适当控制参数uρ(ρ=1,2,···,r)的选取满足<0 时,系统在平衡位置是稳定的.
4 算例
例1已知四阶Birkhoff系统为
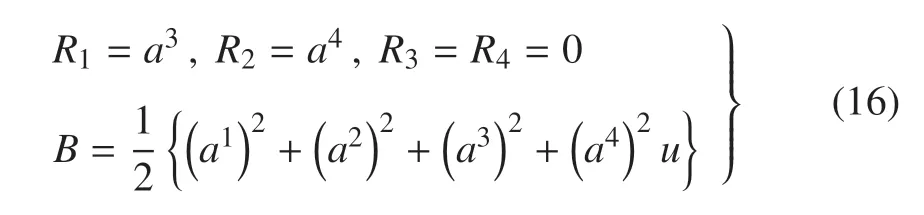
其中u=u(t)为控制参数.选取适当的u使得系统在零解aµ=0 (µ=1,2,3,4)附近是稳定的.
由式(16)可计算出

根据上述所论的方法,欲使B在aµ=0 (µ=1,2,3,4)邻域内正定,应有

根据式(13)可直接得到


例2已知广义Birkhoff系统的Birkhoff函数组,Birkhoff函数以及附加项如下

试求u=u(t)使系统的零解aµ=0 (µ=1,2,3,4)是稳定的.
由式(15)直接得到

很显然,若取u>0,则B在aµ=0 (µ=1,2,3,4)邻域内是正定的.若取


这时系统的平衡是稳定的.
例3广义Birkhoff系统为
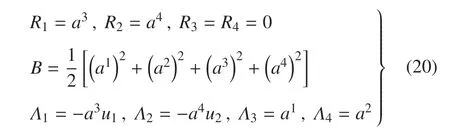
试求ui=ui(t)使系统的零解是稳定的.
同样的由式(15),我们有

因此,当控制参数选取为
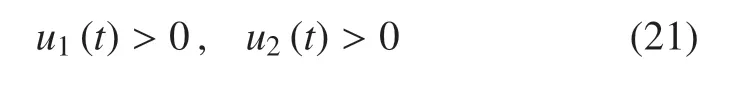
例4已知四阶Birkhoff系统为

其中u=u(t)为控制参数.选取适当的u使得系统在零解aµ=0 (µ=1,2,3,4)附近是稳定的.
首先,由Lyapunov 稳定性可知,若选定B使其正定,则
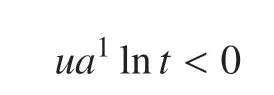
因此,有u<0,a1lnt>0 或u>0,a1lnt<0.
其次,由式(11)可知

当控制参数满足条件

5 结论
有关Birkhoff系统和广义Birkhoff系统的稳定性研究已有一些结果,如文献[6,8-14].大多结果是在给定的Birkhoff函数和Birkhoff函数组下进行研究的.本文在此基础上考虑了包含参数时的情形,研究了当系统的Birkhoff函数或附加项出现控制参数时,通过选取控制参数使得Birkhoff函数B成为定号函数,而其时间导数为与B反号的常号函数,来实现控制系统的平衡稳定性.通过例题讨论并得到了Birkhoff函数及其导数符号变化的几种可能情形.由于完整力学系统和非完整力学系统均可纳入Birkhoff力学系统,因此Birkhoff力学具有一定的普遍性.故本文的思想和方法可以进一步用来研究Hamilton 力学系统,非完整力学系统以及变质量力学系统等的平衡稳定性.
