不同位置的Mn掺杂对ZnO量子点的电磁特性影响

雷 涛 , 符斯列,2, 王春安, 缪 晶, 王琳涵

(1. 华南师范大学 物理与电信工程学院 广东省量子调控工程与材料重点实验室, 广州 510006; 2. 华南师范大学 量子物质研究院 广东省核物质科学与技术重点实验室, 广州 510006; 3. 广东技术大学 电子与信息学院, 广州 510665)

1 引 言

稀磁半导体(Diluted magnetic semiconductors, 简记为DMS)是指非磁性半导体中的部分阳离子被磁性过渡金属元素替代而形成的具有较弱磁性的一种新型半导体[1]. DMS材料可通过对电子自旋的控制来改进传统的半导体技术, 制备具有更小尺寸, 更低功耗, 更快数据处理速度以及数据断电不丢失等优越性能的新型器件[2]. DMS材料的应用主要受制于更高的居里温度, 而Dietl等人[3]通过平均场理论预测了浓度为5%的Mn掺杂ZnO半导体具有高于室温的居里温度. ZnO为直接带隙宽禁带(3.37 eV)半导体, 具有较高的激子束缚能(60 meV),热稳定性高, 优异的光电性能等优越性能, 因此被期待用于制备集电、光、磁三种性能于一体的新型器件的半导体材料, 从而受到广泛的关注与研究[4].

经过多年的研究, 有关Mn掺杂ZnO体材料体系(ZnO:Mn)的电磁特性在实验和理论模拟方面的研究都已较为成熟[5], 并且随着制备工艺的不断提高, 研究的领域已从薄膜转向纳米尺寸. 在实验方面, ZnO已成功制备各种各样的纳米结构, 例如二维的纳米带[6], 一维的纳米棒[7]、纳米线[8], 以及纳米颗粒[9]等等. 在理论方面, 谢建明等人[10]第一性原理计算了Mn掺杂ZnO纳米线. 但是有关ZnO纳米颗粒的第一性原理模拟研究的模型一般为小分子团簇(ZnO)n(n = 2～18)[11-14], 这类模型尺寸很小, 原子数极少, 且多为环状或笼状结构, 与实验[15-18]表明的ZnO纳米颗粒(直径为3 nm以上)内部仍为六方纤锌矿结构的实验结果不符, 因此难以与实验相结合并给实验提供理论参考.

本文构建了六方纤锌矿结构的ZnO量子点(ZnO quantum dot, 简记为ZnO-QD)模型,并采用第一性原理计算方法研究不同位置Mn掺杂对ZnO-QD模型的电磁特性的影响, 所得结果将为实验研究提供有价值的理论参考.

2 模型构建与计算方法

2.1 模型构建

实验表明ZnO纳米颗粒仍然保持六方纤锌矿结构, 参考部分文献对Si量子点的模拟经验[19-21], 本文ZnO-QD模型的构建方法是: 先在ZnO体材料结构中截取一定直径的球状空间区域得到分子簇, 然后采取氢原子钝化表面的悬挂键并对表面原子进行稳定性的修饰, 最后再将分子簇置于简单立方格子中心建立周期性. 本文截取的分子簇直径为1.2 nm, 简单立方格子的边长取2.4 nm(使得相邻分子簇间保持1 nm以上的间距), 得到了ZnO-QD模型, 分子式为Zn45O45H72, 共计162个原子. 整个模型近似球状, 从c轴方向上看呈现六方结构, 如图2(a)所示. 在图2(a)中的(0001)晶面上, 从里到外Zn原子所在位置设为中心(centre), 中间(middle), 表面(surface), 用C、M、S标志. 分别用一个Mn原子替换C、M、S位置上的Zn原子, 来实现三种不同位置的Mn掺杂体系, 用ZnO-QD:Mn表示, 掺杂浓度为2.222%. 其中C格点位置上的Mn掺杂体系用ZnO-QD:Mn-C标识, M格点位置上的Mn掺杂体系用ZnO-QD:Mn-M标识, S格点位置上的Mn掺杂体系用ZnO-QD:Mn-S标识, 其模型分别如图2(b)-(d)所示.

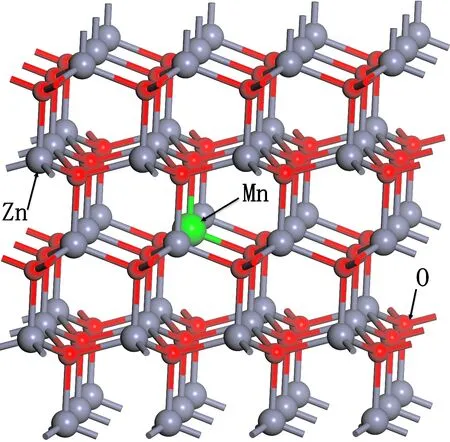
图1 3×4×2 ZnO:Mn超晶胞模型Fig. 1 3×4×2 ZnO:Mn supercell model

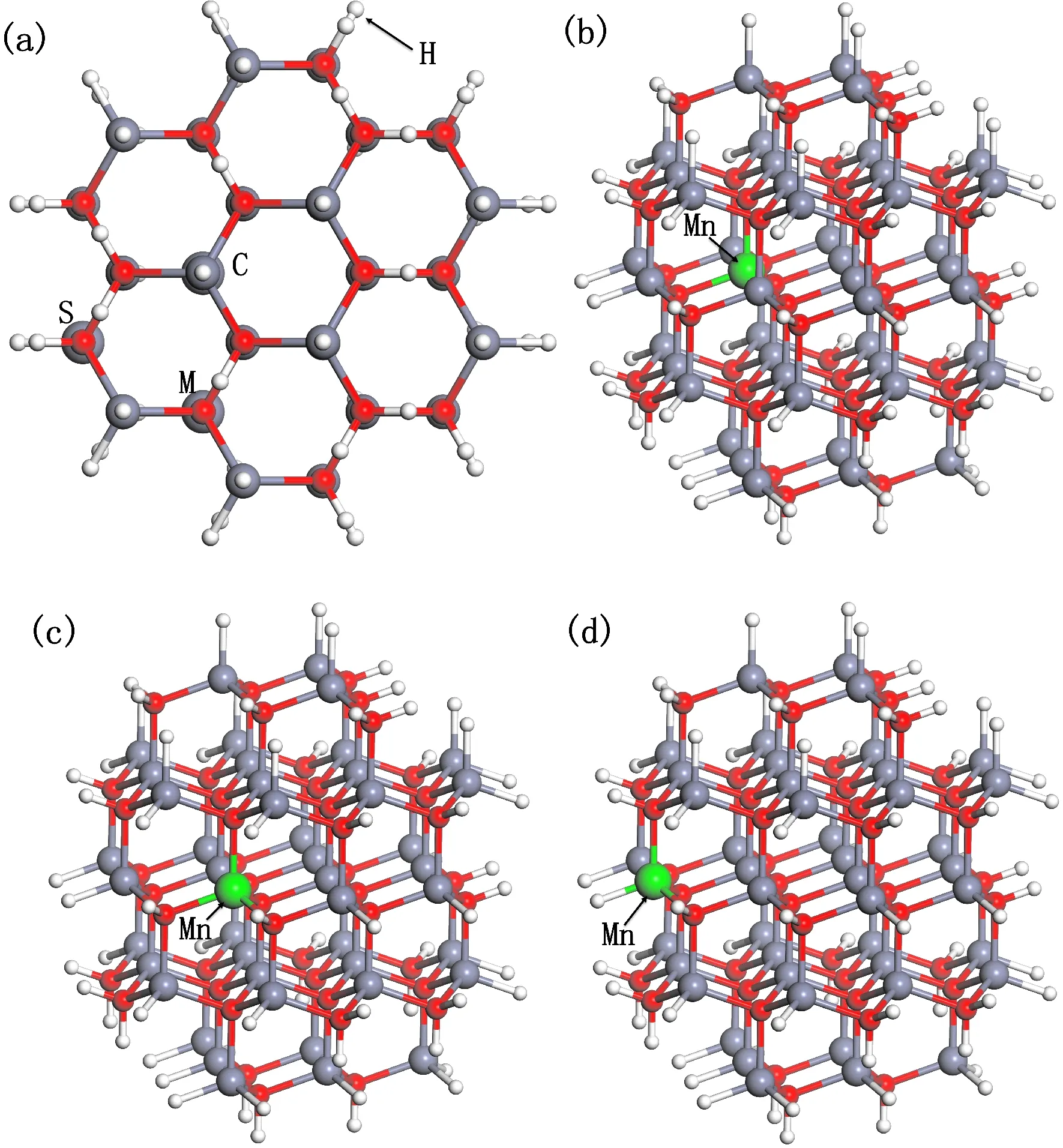
图2 ZnO-QD掺杂前后模型: (a) ZnO-QD在c轴方向的俯视图; (b) ZnO-QD:Mn-C; (c) ZnO-QD:Mn-M; (d) ZnO-QD:Mn-SFig. 2 Models of ZnO-QD before and after doping: (a) Vertical view in c-axis direction of ZnO-QD; (b) ZnO-QD:Mn-C; (c) ZnO-QD:Mn-M; (d) ZnO-QD:Mn-S

2.2 计算方法

计算软件是采用了Materials Studio软件中基于密度泛函数理论平面波赝势展开的CASTEP模块. 选取广义梯度近似(Generalized Gradient Approximation, 简记为GGA)修正的Perdew-Burke-Emzerhof 泛函处理交换关联能, 用超软赝势来描述价电子和离子实之间的相互作用. 几何优化的截断能Ecut= 700 eV. ZnO体材料的k空间网络点取3×4×2, 而ZnO-QD体系则仅取gamma点. 几何优化参数设置如下: 迭代过程中的收敛精度为 2.0×10-5eV·atom-1, 原子间相互作用力收敛标准为0.05 eV·Å-1, 最大位移为0.002 Å·atom-1, 内应力不超过0.1 GPa.

3 结果与讨论

3.1 结构与形成能分析

图3为结构优化后的ZnO-QD模型, 对比图2(a)可知ZnO-QD的结构发生不同程度变形, 尤其表面变形异构十分明显. 这与实验ZnO纳米颗粒结构表面发生变形但其内部仍为六方纤锌矿结构的结果一致[15-8].

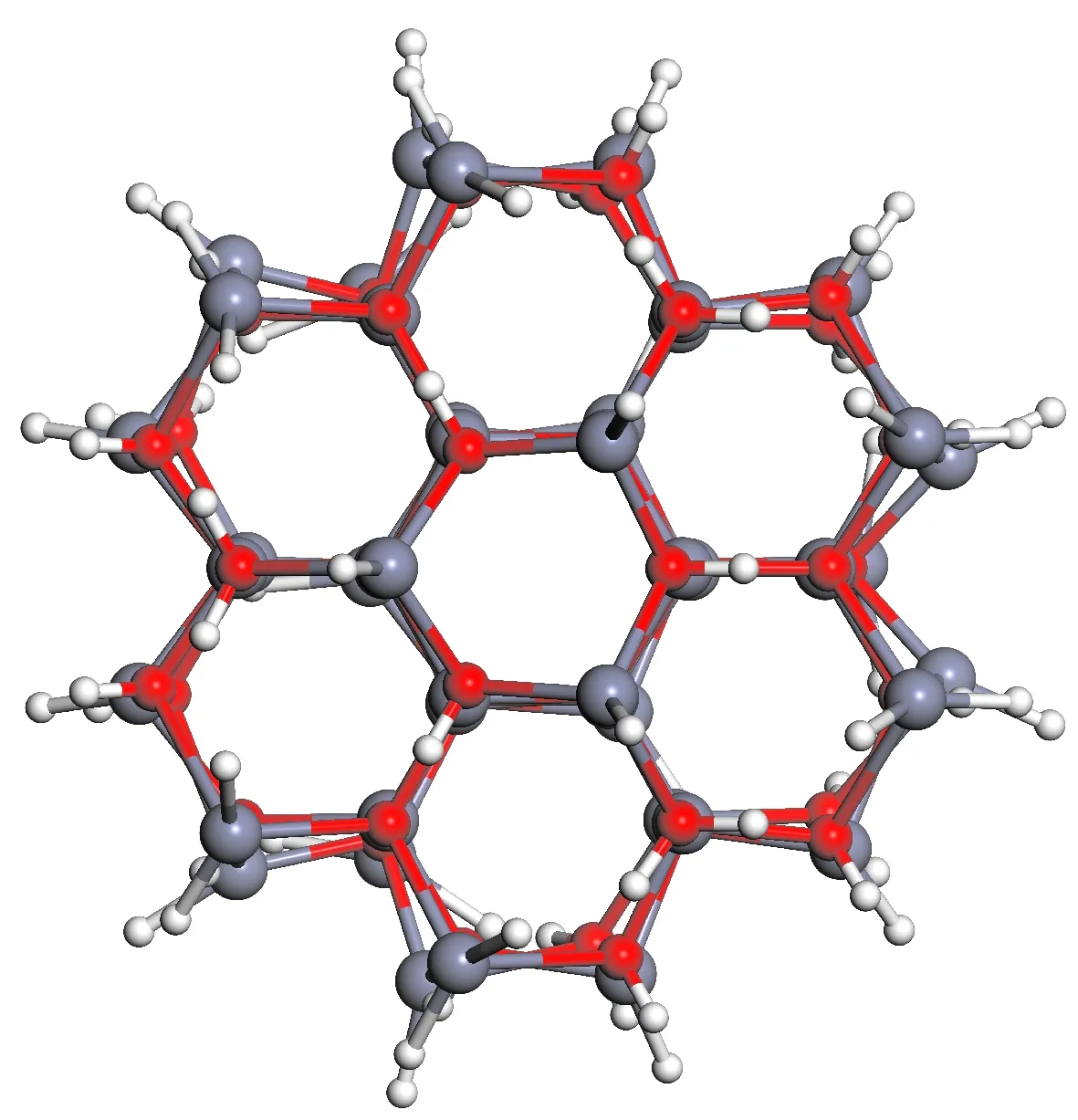
图3 结构优化后的ZnO-QD模型结构Fig. 3 Optimized structure of ZnO-QD model

表1为ZnO各掺杂体系的形成能. 其中杂质X的形成能Ef[X]定义公式[22]为:

Ef[X]=Etot[X]-Etot[ZnO]-∑iniμi

(1)

其中,Etot[X]是掺杂体系的总能量;Etot[ZnO]是ZnO体材料或者量子点结构未掺杂时的总能量;ni代表掺入或移除的原子个数, 掺入为正, 移除为负;μi表示相应原子的化学势. 由表1可知, ZnO:Mn和ZnO-QD:Mn体系的形成能基本相近. 在ZnO-QD:Mn体系中, ZnO-QD:Mn-C模型的形成能与ZnO:Mn十分相近, ZnO-QD:Mn-M体系的形成能最小, ZnO-QD:Mn-S体系的形成能最大, 并且明显增大了许多. 因此推测在ZnO-QD:Mn体系中, 中间掺杂结构最容易形成, 表面掺杂最不易形成.

表1 掺杂ZnO的不同模型结构的形成能

3.2 能带结构与态密度分析

为了了解ZnO的基本特性, 首先对本征ZnO体材料和ZnO:Mn的能带结构和态密度(density of states, 简记为DOS)进行了模拟分析, 其结果如图4(a)-(d)所示. 图4(a)、(b)为本征ZnO体材料的能带结构和总态密度图(total density of states, 简记为TDOS)、分波态密度图(partial density of states, 简记为PDOS), 由图4(a)中的能带图可知, 导带底和价带顶均在G点上, 因此证实本征ZnO体材料是直接带隙半导体. 计算得到的禁带宽度Eg= 0.750 eV, 与以往采用CASTEP计算的结果相近, 但远小于实际实验测量值(3.37 eV), 这是采用GGA方法计算和未考虑缺陷时普遍得到的结果, 但并不影响对ZnO体系电磁特性的理论分析[23]. 由图4(b)可知, 本征ZnO的价带主要由O-2p和Zn-3贡献, 导带主要由Zn-4s、Zn-3p和O-2p贡献.

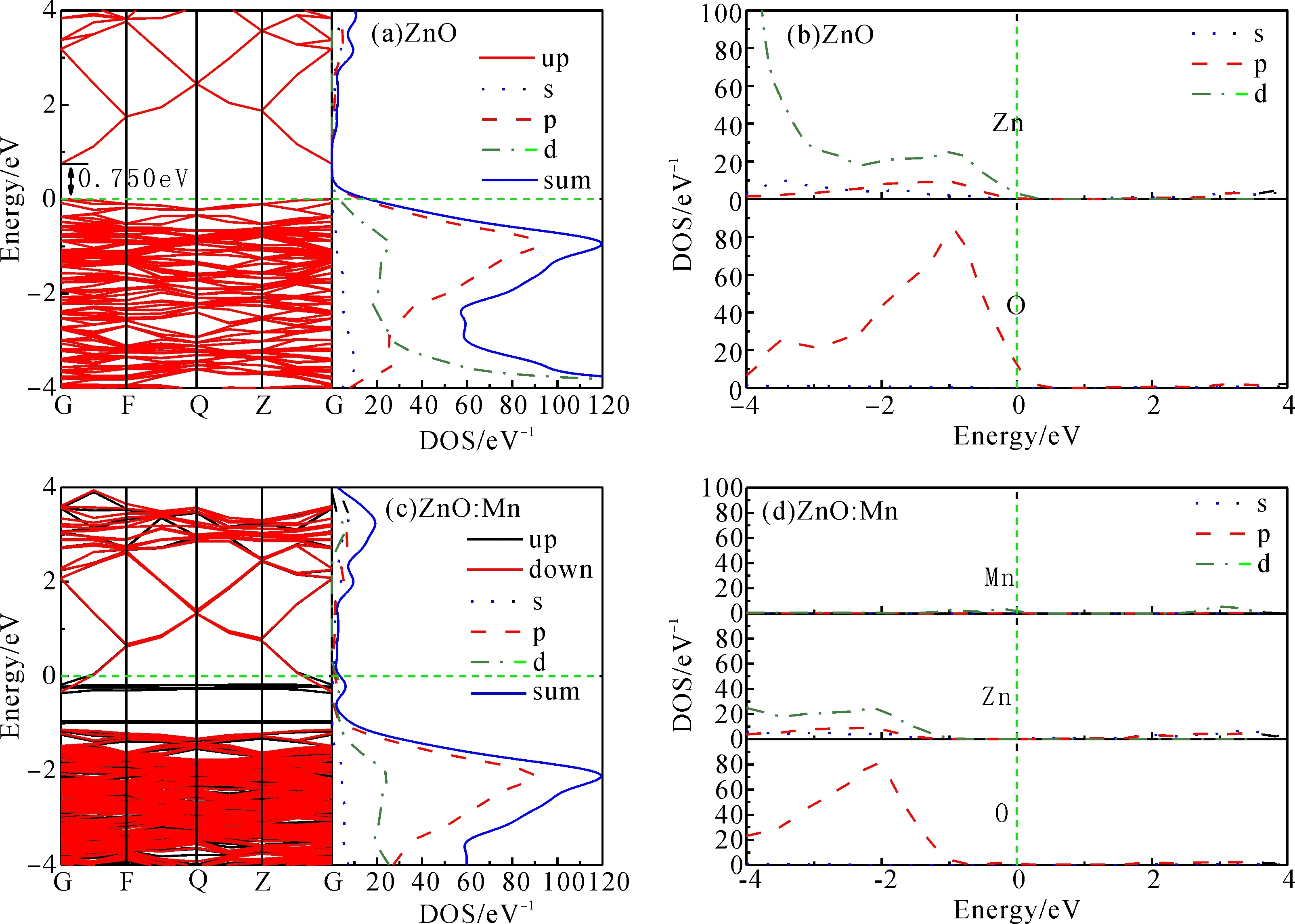
图4 ZnO和ZnO:Mn体系的能带结构图和态密度图Fig.4 The band structures and DOSs of ZnO and ZnO:Mn

图4(c)、(d)为ZnO:Mn体系的能带结构和TDOS、PDOS. 由图4(c)中的能带图可知, ZnO:Mn依然是直接带隙半导体, 但禁带宽度(0.979 eV)相对于本征ZnO略微变宽. 由于Mn的掺杂, 在禁带宽度间形成了一共5条自旋向上的杂质能级, 分别为靠近价带的2条低杂质能级和3条高杂质能级, 并且高杂质能级与导带底相交, 因此使得ZnO:Mn具有半金属性质并增强了导电性能. 由图4(d)可知, Mn态密度主要由Mn-3d态组成, 并主要作用于高导带区(2～4 eV)和禁带宽度间. 位于禁带宽度间的Mn-3d与O-2d相互重叠产生强烈的杂化作用, 使得电子和空穴被束缚在杂质周围形成局域态, 因此引入杂质能级[24].

CASTEP计算本征材料时会将0 eV设置在价带顶, 但引入掺杂后, 会将0 eV设置在杂质能级附近. 虽然带宽不变, 并不影响对材料电磁特性的理论分析, 但不利于准确的细致分析. 因此本文先将ZnO-QD的0 eV设置在禁带中间, 再以导带底(1.210 eV)为能量参考标度对ZnO-QD:Mn体系的能带结构和态密度作平移调整.

图5为ZnO-QD掺杂前后各模型的能带结构, 分别为: (a)ZnO-QD; (b)ZnO-QD:Mn-C; (c)ZnO-QD:Mn-M; (d)ZnO-QD:Mn-S. 图6(a)-(d)为ZnO-QD掺杂前后的PDOS. 由图5(a)可知ZnO-QD的禁带宽度为2.420 eV, 远大于本文计算的ZnO体材料禁带宽度0.750 eV, 这是因为ZnO体材料计算模型为无缺陷周期拓展的理想大模型, 会高估导带的电子分布以致导带底往禁带延伸, 禁带变窄, 而ZnO-QD的计算模型为单一有限小模型, 因此会更加接近实验值. 在钝化ZnO量子点模型时引入了大量的H原子掺杂, 但H掺杂并不会产生多余的电子与空穴. 由图6(a)可知H原子的态密度主要分布于高价带(-2～-1 eV)和高导带. 高价带的H-1s与Zn和O的各轨道电子产生强相互作用, 并由于H原子数较多, 以致Zn和O的态密度发生变形, 产生高峰值, 从而形成新的高价带, 导致价带顶往高能方向移动, 禁带变窄.

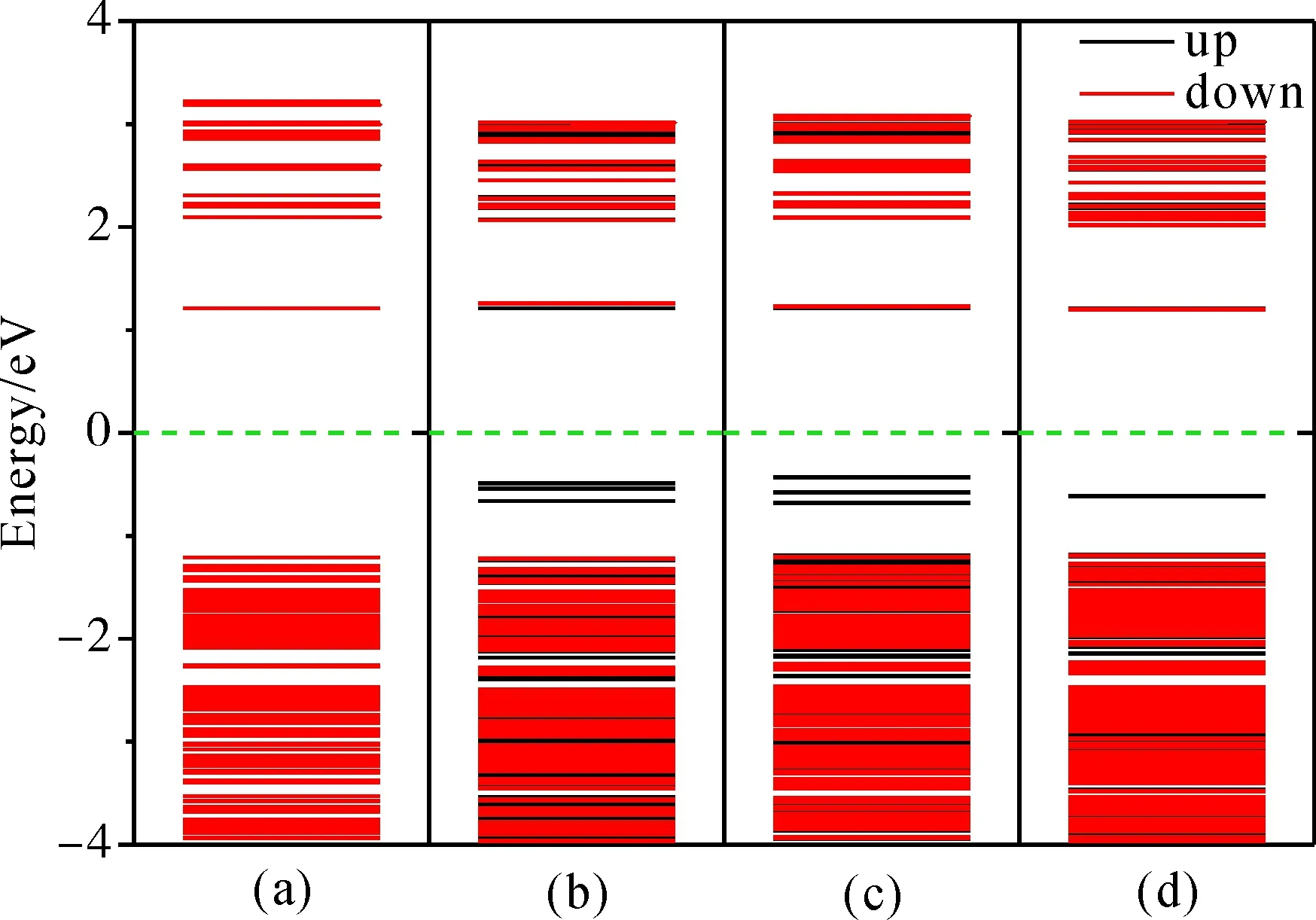
图5 ZnO-QD掺杂前后的能带结构: (a) ZnO-QD; (b) ZnO-QD:Mn-C; (c) ZnO-QD:Mn-M; (d) ZnO-QD:Mn-SFig. 5 The band structures of ZnO-QD before and after doping: (a) ZnO-QD; (b) ZnO-QD:Mn-C; (c) ZnO-QD:Mn-M; (d) ZnO-QD:Mn-S

图6 ZnO-QD掺杂前后的PDOSsFig. 6 The PDOSs of ZnO-QD before and after doping

图7(a)为不同位置掺杂时Mn的自旋态密度, 图7(b)为掺杂前后ZnO-QD的总自旋态密度, 其中Q代表ZnO-QD, C代表ZnO-QD:Mn-C, M代表ZnO-QD:Mn-M, S代表ZnO-QD:Mn-S. 由图6(b)- (d)可知, Mn的态密度主要分布于高导带(2～4eV)、下禁带(-1～0 eV)

和高价带, 结合图7(b)可以发现, 导带底附近的态密度, 在掺杂前后均无明显变化, 这说明Mn的掺杂及掺杂位置的改变对导带底的影响极小, 使得让ZnO-QD的导带底作为ZnO-QD掺杂前后的能量参考标度具有一定的意义.

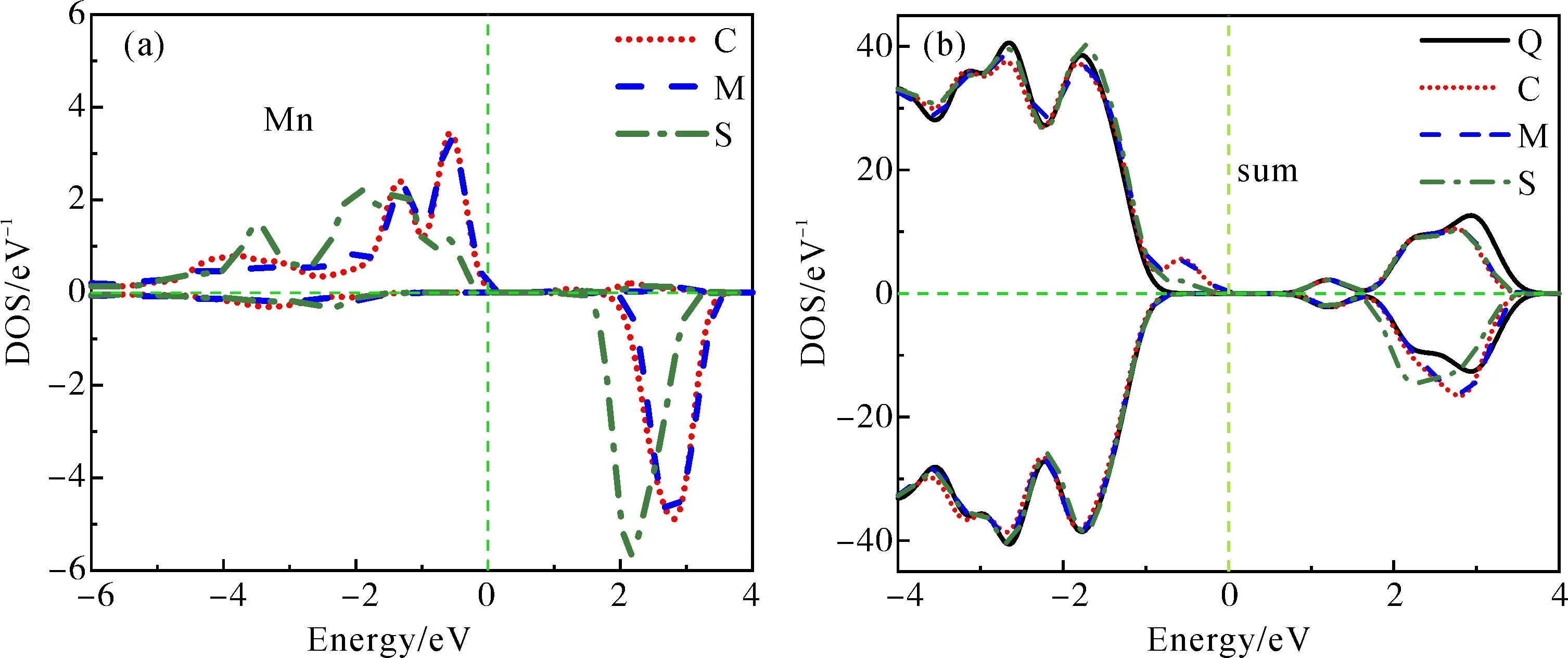
图7 ZnO-QD掺杂前后的自旋态密度: (a) Mn; (b) 态密度总和Fig. 7 The densities of spin states of ZnO-QD before and after doping: (a) Mn; (b) sum

由图5(b)、(c)的能带图可知, ZnO-QD:Mn-C和ZnO-QD:Mn-M禁带中间存在3条自旋向上的靠近价带的杂质能级, 比ZnO:Mn体系少了2条杂质能级, 结合图7(a)可知, Mn在0eV以下的态密度主要分在下禁带和高价带, 因此2条低杂质能级进入价带, 从而证实前文分析的由于大量H原子的钝化使得价带往高能方向延伸以致禁带宽度变窄的结论. 而图5(d)的能带图显示ZnO-QD:Mn-S的禁带中间只有一条杂质能级, 这是由于Mn的掺杂位置变成表面, 使得Mn原子四周原本成键的4个氧原子中的1个被H原子替代所导致的. 结合图6(b)-(d)可知, Mn中心掺杂和中间掺杂时, 杂质能级主要是由Mn-3d和O-2d贡献, 并且Mn的自旋向上部分态密度主要集中在禁带间, 因此依然产生3条杂质能级, 但Mn表面掺杂时, 杂质能级主要由Mn-3d和H-1s贡献, 并且由于1个H原子替换1个O原子与Mn成键后, 使得Mn的态密度往低能方向平移, 而自旋向上部分不仅变得平缓而且大部分已进入价带, 以致禁带间只有1条杂质能级.

为更进一步分析ZnO-QD:Mn体系的导电性, 图8为ZnO-QD:Mn体系中杂质能级上的总态密度. 表2为ZnO-QD掺杂前后各自旋能级和带宽,Ec为导带底,Ev为价带顶,Ei为杂质能级顶端,ΔEci=Ec-Ei为杂质电离能. 由表2可知, 随着Mn掺杂位置不同, 相对于未掺杂时Eg的变化很小, 但ΔEci会发生明显变化, 中间掺杂最小, 表面掺杂最大. 结合图8, 中间和中心掺杂时杂质能级上的态密度分布基本一致, 而表面掺杂时杂质能级上的态密度明显偏低. 因此中间掺杂导电性略强于中心掺杂, 表面掺杂导电性明显偏弱.

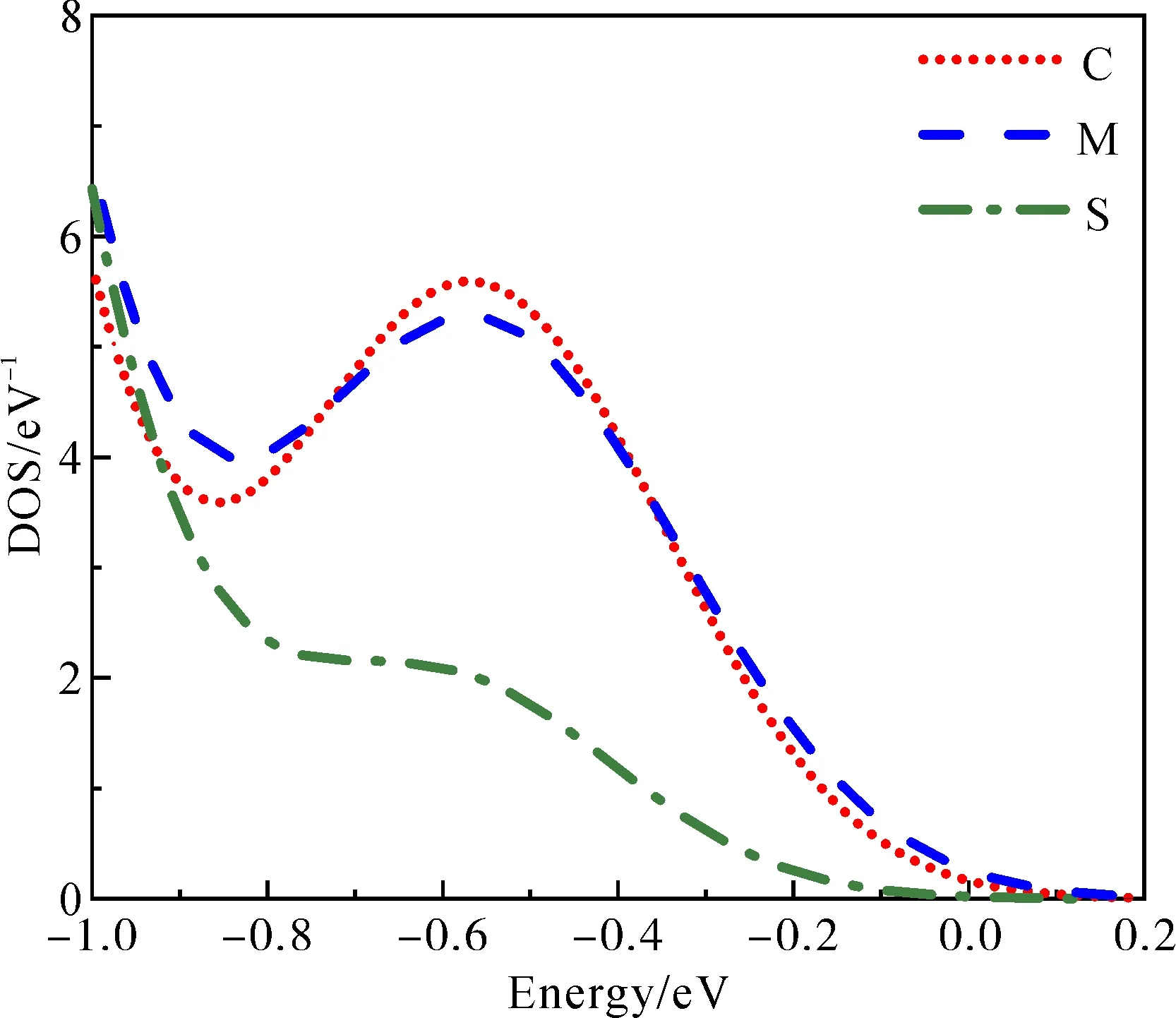
图8 ZnO-QD:Mn体系杂质能级上总态密度Fig. 8 The TDOS at impurity levels in ZnO-QD:Mn system

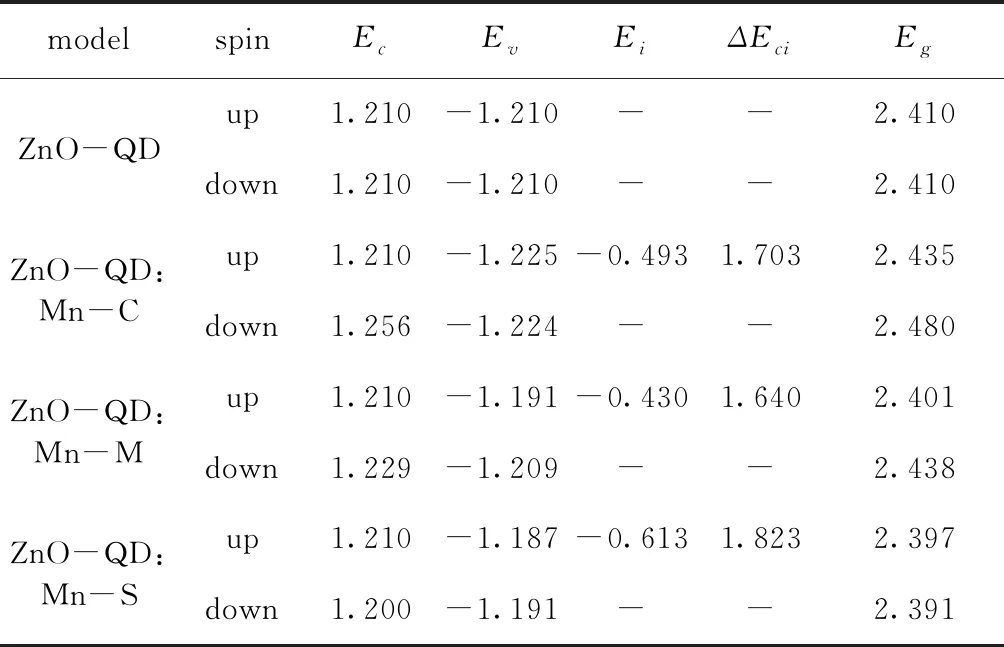
表2 ZnO-QD掺杂前后各自旋能级与带宽

3.3 磁性分析

图9(a)-(d)为ZnO-QD掺杂前后的自旋分波态密度. 图9(a)显示ZnO-QD的自旋向上与向下态密度完全一致, 因此没有磁性. 图9(b)-(d)则表明Mn掺杂ZnO-QD会使得体系高导带和下禁带的自旋向上和向下态密度发生明显不对称现象, 以致产生磁性. 并且可以发现, 中心和中间掺杂时, 磁性主要来源于Mn-3d和O-2p的相互作用, 而表面掺杂时, 磁性主要来源于Mn-3d和H-1s的相互作用. 这与前文分析的杂质能级的主要来源一致.

表3展示了ZnO:Mn和ZnO-QD:Mn体系总磁矩和各原子总磁矩. ZnO-QD:Mn体系中, 随着Mn掺杂位置由里向外变化时, Mn和H原子总磁矩会逐渐增大, Zn和O原子总磁矩会逐渐减小, 但是体系总磁矩基本保持不变. 由于ZnO-QD:Mn体系的总磁矩不为零, 并且体系中只有一个磁性原子而相邻ZnO-QD:Mn的相互影响很小, 因此一个Mn掺杂的ZnO-QD体系具有铁磁性.

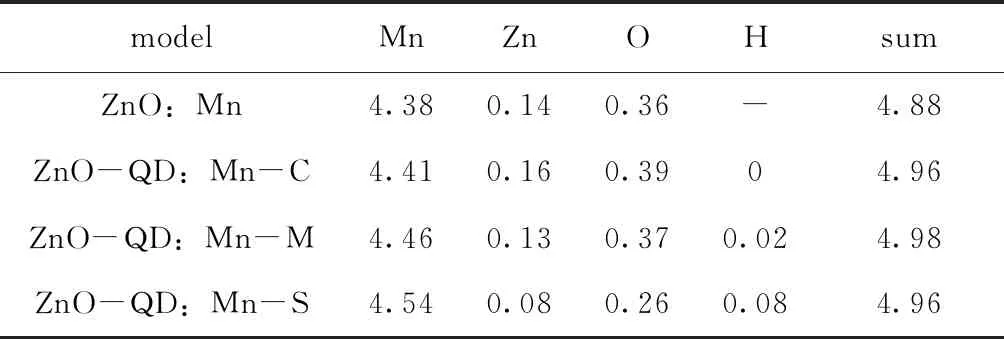
表3 ZnO:Mn和ZnO-QD:Mn总磁矩和各原子总磁矩

4 结 论

本文构建了六方纤锌矿结构并经H钝化的直径为1.2 nm的ZnO量子点模型(Zn45O45H72, 并经H钝化), 并采用基于密度泛函理论的第一性原理平面波超软赝势法对在中心、中间、表面三种不同位置掺杂的ZnO-QD:Mn体系的形成能、能带结构、态密度和磁矩进行分析. 结果表明: 大量H原子钝化会使得ZnO-QD的禁带宽度变窄; 中间位置掺杂时, 体系的结合能最低, 同时导电性能最好; 中心位置掺杂略劣于中间位置掺杂; 而表面位置掺杂时, 结合能明显偏高, 同时导电性能明显减弱. 在磁性方面, 随着掺杂位置变化,体系中各原子的总磁矩和磁矩分布会发生明显变化, 但体系的总磁矩基本不变, 并且单Mn掺杂的

图9 ZnO-QD掺杂前后的自旋分波态密度Fig. 9 The partial densities of spin states of ZnO-QD before and after doping

ZnO-QD体系为铁磁性. 中心与中间掺杂时, 杂质能级和磁性主要来源于Mn-3d和O-2p的相互作用, 而表面掺杂时, 杂质能级和磁性主要来源于Mn-3d和H-1s的相互作用, 并且Mn的态密度分布会明显往低能方向转移. 总之，在实验过程中想要得到良好电磁特性的Mn掺杂ZnO纳米颗粒, 最好避免Mn的表面掺杂.