氢原子在红外激光和极紫外脉冲组合场中的阈上电离

王 娜， 景文泉， 管 仲， 杨增强， 赵松峰

(1.西北师范大学 物理与电子工程学院， 兰州 730070； 2.陕西科技大学 文理学院物理系， 西安 710021)

1 引 言

自1979年Agostini等人首次实验观测到原子的阈上电离(ATI)现象以来[1]，原子、分子在激光场中的阈上电离已成为强场物理领域的热点课题[2-4]，譬如光电子能谱对激光绝对载波相位(CEP)[5,6]和啁啾率[7-9]的依赖、激光强度依赖的类共振结构[10-14]、低能结构[15-18]等.基于定量重散射理论[4]，原子的光电离散射截面、激光的参数(如CEP、强度和脉冲宽度)都可以从高能光电子动量谱中提取出来[19].

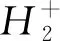
本文通过求解氢原子(H)在强红外激光与XUV脉冲组合场驱动下的TDSE,采用光电子总能谱和二维(2D)电子动量谱全面地研究阈上电离过程中的波包干涉现象，包括XUV光脉冲的强度、角频率及时间延迟对干涉结构的影响，结果表明IR+XUV方法可选择性地增强高能阈上电离谱.

2 理论方法

在偶极近似和长度规范下，三维氢原子的TDSE可以表示为：

(1)

H0为无外场的原子哈密顿量，而原子与场的相互作用项Hi(t)为：

Hi(t)=r·E(t)，

(2)

E(t)是激光的电场.总的矢量势A(t)=Air(t)+AXUV(t)对应的电场为：

(3)

含时波函数Ψ(r,t)展开为：

(4)

将末态波函数投影到一个给定动量P的连续电子的本征态上，从而可得到二维动量谱：

(5)

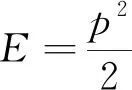
(6)

在方程(5)中对θ进行积分,可获得光电子的能量谱：

(7)

在本文中，考虑一个飞秒(fs)激光脉冲，它具有高斯包络形式[7,33].假设激光脉冲沿z轴线性偏振，则红外激光和极紫外脉冲的矢势[31]分别为：

(8)

(9)

在计算中，红外激光脉冲取固定的参数：即激光峰值强度Iir=1.2×1014W/cm2，中心波长λir=800 nm，半高全宽(FWHM)τir=7 fs.在此强度下，仅红外激光场单独作用就能使氢原子显著电离.本文中，通过改变XUV脉冲的参数，如XUV脉冲的峰值强度、角频率和时间延迟，研究这些参数对氢原子光电子能谱中干涉结构的影响. 在本文中，我们选取空间范围rmax=1600 a.u.，最大分波数lmax=120，采用非均匀时间撒点，IR和XUV的重叠区域时间步长dt1=0.02 a.u.，非重叠区域时间步长dt2=0.1 a. u..

3 数值结果和讨论

3.1 光电子能谱和二维动量谱中的干涉增强区域

首先，我们选取一个长XUV脉冲，其参数为：峰值强度IXUV=1×1012W/cm2，中心波长λXUV=50 nm, 电子吸收单个XUV光子就能到达连续态，脉冲宽度为168个光学周期. 图1(a)展示了IR和XUV脉冲的电场强度. 图1(b)为IR和IR+XUV激光脉冲分别作用下氢原子的光电子能谱. 从图中可以发现，与仅由强红外场作用下的氢原子光电子能谱相比，组合场下能谱在3～9Up能量区间的光电子产额被显著增强(本文中将称为增强区域). 为了更直观地展示干涉增强现象，图1(c)和(d)分别给出了由强红外场单独作用下和组合场作用下的二维光电子动量谱，为了简单起见，本文对所有的二维动量谱进行了归一化. 可以看出，组合场作用下的二维动量谱有更加复杂的结构，XUV脉冲的加入使得动量平行分量在1.4～2 a.u.区域内出现了明显的干涉增强结构.

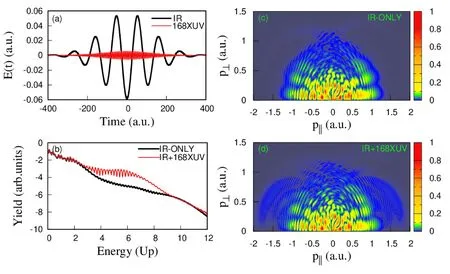
图1 (a) 激光脉冲的电场强度, (b) 氢原子光电子能谱的比较, (c) 红外场单独作用下H的二维光电子动量谱, (d) 组合场作用下H的二维光电子动量谱.Fig. 1 (a) The electric field of laser pulses. (b) Comparison of photoelectron energy spectra of H. (c) 2D photoelectron momentum spectra of H driven by the infrared laser only. (d) 2D photoelectron momentum spectra of H in the combined field.

为了研究光电子能谱对XUV脉冲的依懒性，我们选取半高全宽τXUV=0.5 fs且延迟时间不同的若干XUV脉冲组成脉冲链，其它激光场参数与图(1)相同.图2(a)为IR激光电场峰值处加入7个XUV脉冲的电场，图2(b)则为IR矢势峰值处加入6个XUV脉冲的电场.图2(c)给出了相应的氢原子光电子能谱.从图中可看出，当各个XUV脉冲加在IR激光电场峰值处时，光电子能谱中没有出现干涉增强现象，而当各个XUV脉冲加在IR矢势峰值处时，光电子能谱在3～9Up能量范围内展现出明显的干涉增强结构，而且与加入图1(b)中所示的XUV脉冲所得的光电子能谱基本一致. 这说明干涉增强主要来源于各矢势峰值处单光子电离的电子波包间的相长干涉.

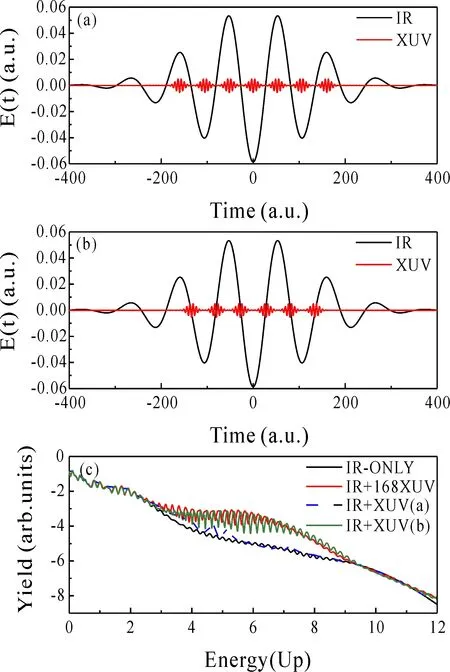
图2 激光脉冲的电场强度: (a) XUV脉冲的时间延迟分别为：t1=-160 a.u.,t2=-105 a.u.,t3=-52 a.u.,t4=0 a.u.,t5=52 a.u.,t6=105 a.u.和 t7=160 a.u., (b) XUV脉冲的时间延迟分别为：t1=-134 a.u.,t2=-80 a.u.,t3=-28 a.u.,t4=28 a.u.,t5=80 a.u.和 t6=134 a.u., (c) 氢原子光电子能谱的比较，仅IR激光 (黑色粗实线)，IR+168XUV (红色中实线)，IR+XUV(a) (蓝色划线)和IR+XUV(b) (绿色细实线).Fig. 2 The electric field of laser pulses: (a) The time delays of XUV pulses are t1=-160 a.u.,t2=-105 a.u., t3=-52 a.u.,t4=0 a.u.,t5=52 a.u.,t6=105 a.u. and t7=160 a.u., respectively. (b) The time delays of XUV pulses are t1=-134 a.u.,t2=-80 a.u.,t3=-28 a.u.,t4=28 a.u.,t5=80 a.u. and t6=134 a.u., respectively. (c) Comparison of photoelectron energy spectra of H, only the IR laser (black thick solid), IR + 168 XUV (red medium solid), IR + XUV (a) (blue dashed) and IR + XUV (b) (green thin solid).

为了探究光电子能谱中干涉增强结构的来源，我们在矢势峰值处分别加入一个时间延迟t1=-28 a.u.和t2=80 a.u.XUV脉冲，如图3(a)和(b)所示;另外，在时间延迟t1=-28 a.u.和t2=80 a.u.处同时加入两个XUV脉冲，如图3(c)所示. 图3(d)给出了对应的光电子能谱图，从图中可看出，在IR+XUV(a)组合场驱动下干涉增强区域向低能方向压缩，而IR+XUV(b)情况下则向高能方向压缩.在IR+XUV(c)情况下,光电子能谱的增强区域和干涉结构与IR+168XUV情况比较接近.这表明干涉增强结构是各矢势峰值处电离的电子波包间的相长干涉所致.

将图3(c)所示的两个XUV脉冲向左平移半个周期，如图4(a)所示，XUV(1)的时间延迟分别为：t1=-28 a.u.和t2=80 a.u.；XUV(2)的时间延迟分别为：t1=-80 a.u.和t2=28 a.u.. 图4(b)比较了氢原子的光电子能谱，在这两种情况下，干涉增强结构的差异比较小. 图4(c)和(d)给出了分别加入XUV(1)和XUV(2)相应的二维光电子动量谱，可以看出，干涉增强分别发生在p∥<0和p∥>0的区域.

3.2 干涉增强结构对XUV脉冲强度、以及光子能量的依赖

为了研究干涉增强结构对XUV脉冲强度、以及光子能量的依赖性，我们选取图1(a)所示的IR激光和XUV脉冲.图5(a)给出了中心波长(λXUV=50 nm)和半高全宽(τXUV=7 fs)不变，峰值强度不同的XUV脉冲和IR激光共同驱动下的氢原子光电子能谱.可以发现，干涉增强随着XUV脉冲强度的减小而减弱.图5(b)为XUV脉冲的半高全宽(τXUV=7 fs)和强度(IXUV=1×1012W/cm2)不变，中心波长不同的XUV脉冲和IR激光共同驱动下的光电子能谱.可以清晰地看到，随着XUV波长的增大，干涉增强区域向低能量方向移动.

为了理解图5(b)中光电子能谱截止位置随XUV脉冲波长的移动，我们采用经典力学图像，即电子的运动满足牛顿运动方程：∂P(t)/∂t=-Eir(t).根据正则动量守恒，探测器处的光电子动量为：

P(t∞)=P0-Air(t0)，

(10)

其中t0为电子的电离时刻.当XUV脉冲加入红外场矢势峰值最大处时，光电子获得最高的能量，由(10)式可以近似得到相应的截止能量为：

(11)

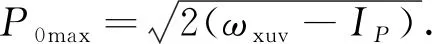
4 结 论

通过数值求解三维含时薛定谔方程，理论研究了氢原子在强红外激光和XUV脉冲组合场中的阈上电离.研究发现，当在强红外激光的适当位置加入XUV脉冲，在光电子能谱和二维动量谱中均呈现出明显的干涉增强结构，这是由不同时刻单光子电离的电子波包之间的相长干涉导致的.干涉增强的强弱(位置)对XUV脉冲的强度(波长)有很强的依赖.用红外激光和XUV脉冲驱动原子、分子的方案可实现对高能阈上电离电子产额的选择性增强.

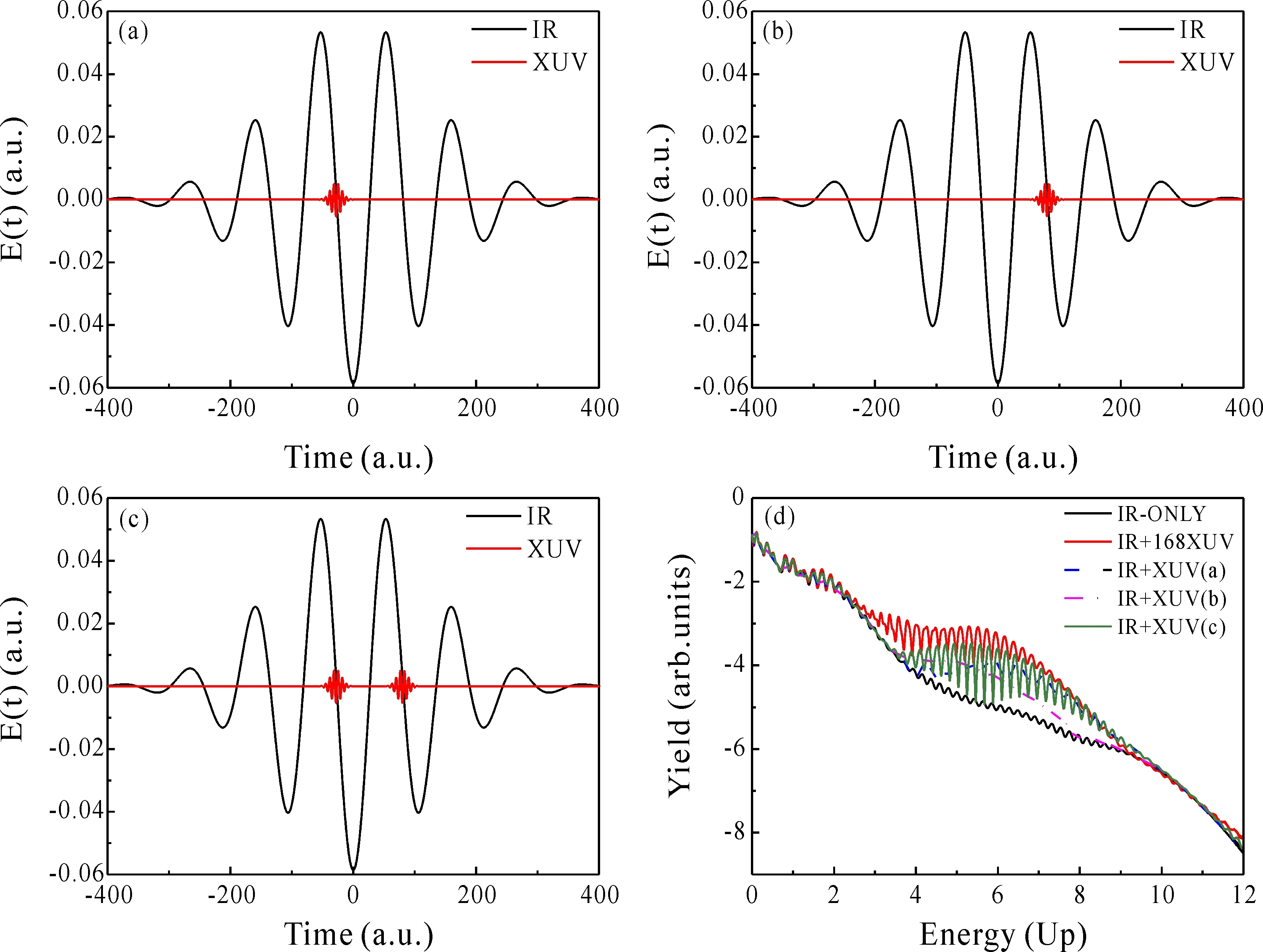
图3 激光脉冲的电场强度: (a) XUV脉冲的时间延迟为：t1=-28 a.u., (b) XUV脉冲的时间延迟为：t1=80 a.u., (c) XUV脉冲的时间延迟分别为：t1=-28 a.u.和 t2=80 a.u., (d) 氢原子光电子能谱的比较，仅IR激光(黑色粗实线)，IR+168XUV (红色中实线)，IR+XUV(a) (蓝色划线)，IR+XUV(b) (紫色点划线)和IR+XUV(c) (绿色细实线).Fig. 3 The electric field of laser pulses：(a) For the time delay of XUV pulse t1=-28 a.u.. (b) For the time delay of XUV pulse t1=80 a.u.. (c) For the time delays of XUV pulses are t1=-28 a.u. and t2=80 a.u., respectively. (d) Comparison of photoelectron energy spectra of H, only the IR laser (black thick solid), IR + 168 XUV (red medium solid), IR + XUV (a) (blue dashed), IR+XUV(b) (purple dot-dashed), IR+XUV(c) (green thin solid).

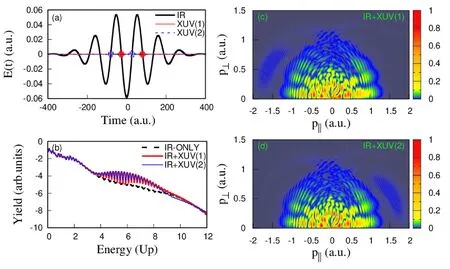
图4 (a) 激光脉冲的电场强度，XUV(1)脉冲的时间延迟分别为：t1=-28 a.u.和t2=80 a.u.，XUV(2)脉冲的时间延迟分别为：t1=-80 a.u.和t2=28 a.u., (b) 氢原子光电子能谱的比较，仅IR激光 (黑色划线)，IR+XUV(1) (红色粗实线)和IR+XUV(2) (蓝色细实线), (c) 红外场和XUV(1)作用下的二维光电子动量谱, (d) 红外场和XUV(2)作用下的二维光电子动量谱.Fig. 4 (a) The electric field of laser pulses. The time delays of XUV(1) pulses are t1=-28 a.u. and, t2=80 a.u., respectively. The time delays of XUV(2) pulses are t1=-80 a.u. and t2=28 a.u., respectively. (b) Comparison of photoelectron energy spectra of H, only the IR laser (black dashed), IR+XUV(1) (red thick solid), IR+XUV(2) (blue thin solid). (c) 2D photoelectron momentum spectra for IR+XUV(1) case. (d) 2D photoelectron momentum spectra for IR+XUV(2) case.