调控硼硫掺杂比实现金刚石n型转变的研究

李宗宝, 王 霞, 李 勇

(铜仁学院 材料与化学工程学院， 铜仁 554300)

1 引 言

由于强的sp3杂化轨道而形成的C-C四面体结构使金刚石兼具大的硬度(HV100 GPa)、高的热导率(20 W·cm-1· K-1)、宽的透光波段(0.22-2.5 μm)、高的杨氏模量(1000 GPa)和高的电阻率(1016Ω·cm)等优点，在工业、科技、国防、微电子等行业得到了广泛的应用，尤其高温高压环境下的稳定特性使其成为构建极端环境器件的重要材料[1-5]. 随着金刚石大单晶合成工艺的日趋成熟，特种功能金刚石的制备及在特定领域的应用成为研究的重点.

为有效调控金刚石的禁带宽度(～5.5 eV) ，通过元素掺杂的方式可以引入受主或施主原子，从而获得p型或n型金刚石半导体[6-10]. 然而，小剂量单一元素掺杂对于提升金刚石的半导体性能(电输运特性)并不明显，而采用重掺杂的方式易引入晶格畸变，进而严重影响金刚石的机械性能[11, 12]. 同时，虽然实验上已获得以硼元素掺杂为代表的典型p型半导体金刚石材料[12-14]，但是由于理想施主元素的缺失，具有优良电输运特性的n型半导体金刚石却鲜见报道.

对于单一元素掺杂，虽然理论证明采用氮元素替位金刚石中的碳元素会为晶胞中提供一个额外电子，使其形成n型半导体(图1d)[15]. 然而，实验结果证明，低浓度氮掺杂较难获得n半导体. 同时，吉林大学马红安教授课题组合成的高浓度氮掺杂绿色金刚石大单晶亦不具备导电性[16]. 另外，采用同主族的磷元素掺杂易在金刚石中形成深能级缺陷及磷团聚现象，亦不能赋予金刚石n型半导体特性[14]. 大量实验证明，通过采用单一元素掺杂来获得n型金刚石半导体存在诸多困难.

采用多元素协同掺杂除能有效避免因单一掺杂原子半径不匹配造成大的晶格畸变外，还能够通过不同掺杂原子的电子协同实现对能带的有效调控[17-20]，进一步获得理想n型金刚石半导体. 基于硼(B)、硫(S)元素的协同掺杂，本课题组首次获得了p、n型可调协金刚石半导体[21]. 然而, 其内含的具体物理机理尚未深入理解. 基于此，本文采用基于密度泛函理论的第一性原理方法，以形成能为主要判据，研究了B、S不同比例单掺杂及共掺杂金刚石的可能形式，通过对电子结构的比较，给出了B/S掺杂改性的微观机理，为后续实验上更好的获得n型金刚石半导体提供理论支撑.

2 理论计算方法

为从原子角度获得B-S协同掺杂在金刚石中的可能存在形式及对金刚石电学性能的影响，采用Vienna Ab-initio Simulation Package(VASP)软件包对其相关性能进行计算[22]. 在周期性边界条件下，采用GGA+PBE方法处理电子间的交换关联能[23]. 由于需要对不同掺杂浓度进行比较，我们在基础原胞(如图1a)的基础上采用2×2×2的超晶胞(共64个原子)进行建模. 由于实验中元素掺杂的浓度较低，造成的晶格畸变较小可以忽略，因此本文固定了晶角大小而只对掺杂后的晶格常数进行优化，如表1所示. 在倒格矢空间，平面波截断能取为600 eV，k点取值为6×6×6[24]，优化及性能计算中采用收敛精度为1×10-6eV/atom，原子弛豫精度为1×10-4Å. 虽然GGA会低估金刚石的禁带宽度，但仍能较好反映出元素掺杂对金刚石能带变化趋势的影响[17]，并进一步反映出对电学性能的影响.

表1 不同原子掺杂金刚石结构的晶格常数及部分键长变化

形成能是表征元素掺杂稳定性、掺杂量及元素掺杂竞争机制的特征量. 本文计算了单一元素不同掺杂比例及B-S元素协同掺杂过程中的形成能(Eform)，采用公式如下[17]：

Eform=Edoped-Ediamond-n·μcoped+n·μC

(1)

式中Edoped和Ediamond分别为掺杂后金刚石及纯金刚石的能量，μcoped和μC为掺杂原子和碳原子的能量，n为掺杂原子数目. 在同类元素不同比例掺杂中，为探究形成能随掺杂原子数量的变化关系，进一步计算了平均掺杂形成能：

Emf=Eform/n

(2)

进一步，为探究掺杂元素的分散效果，还讨论了多掺杂原子近邻及次近邻掺杂情况，并对相应形成能进行比较.

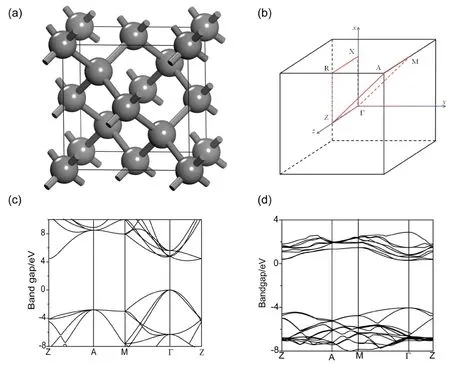
图1 (a)计算用金刚石单晶胞结构示意图,(b)金刚石的布里渊区及高对称点示意图,(c)金刚石单晶胞能带结构,(d) 微量N掺杂金刚石的能带结构.Fig. 1 (a) Crystal structure of diamond, (b) Schematic diagram of Brillouin zone and high symmetry point of diamond. Band structure of the pure diamond (c), and diamond with N doping (d).

3 结果与讨论

3.1 不同掺杂的晶格结构

基于温度梯度实验合成法[21]，掺杂元素以替位形式存于金刚石晶体. 在实验中并不能排除掺杂元素析出问题，因此元素掺杂形成能的相对大小可以有效反馈实验中杂质原子掺杂的难易度. 基于B、S元素在金刚石中的可能存在形式，计算了其不同比例掺杂金刚石的总形成能，同时采用平均形成能评估原子掺杂的难易度，如图2所示. 由图2(a)可以看出，(1)单个B原子替位掺杂形成能较低(～4.3 eV)，证明其易于形成对金刚石的掺杂；(2)双B原子及三个B原子共掺杂的平均形成能低于单B原子掺杂形成能，且随掺杂浓度的增加，平均形成能变化不大，证明B原子可以实现大比例替位掺杂金刚石；(3)大比例B原子共掺杂中，近邻掺杂的平均形成能最低，证明B原子对金刚石晶体进行掺杂时易于在晶体中形成团聚，与实验结果相吻合[21]；(4)随着B掺杂比例的变化，金刚石晶胞参数变化较小(表1)，证明B掺杂不易造成金刚石晶格结构的畸变，从而对金刚石硬度等的影响较小，为较理想的掺杂元素. 究其原因为B原子(0.95 Å)与C原子相仿的原子半径大小(0.86 Å). 对于S元素掺杂，由图2(b)可以看出：(1)单个S原子掺杂的平均形成能均远大于单个B原子掺杂的平均形成能(约为后者的3倍)，证明S掺杂难于B掺杂；(2)多S原子共掺杂平均形成能小于单一S元素掺杂形成能，同时非近邻平均形成能最低，证明S单掺杂倾向于分散替位掺杂形式. 由于S原子半径(1.04 Å)远大于C原子半径，使S掺杂易造成金刚石晶格畸变(表1)，进而需较大能量实现S替位掺杂. 再次，由于B元素掺杂不存在明显的阈值，对于B、S协同掺杂，影响其掺杂浓度的因素主要源于S元素的掺杂比例. 为此，我们主要讨论B∶S=1∶1，2∶1和1∶2三种不同比例掺杂的形成能，如图2c所示. 通过比较可以看出，B与S以2∶1比例近邻协同掺杂时的平均形成能最低，应为最可能出现的稳定协同掺杂存在形式. B-B-S近邻结构单元的出现，使B替位所形成的晶格收缩与S形成的晶格膨胀有效抵消，从而使掺杂后的金刚石晶体结构具备更好的热力学稳定性.

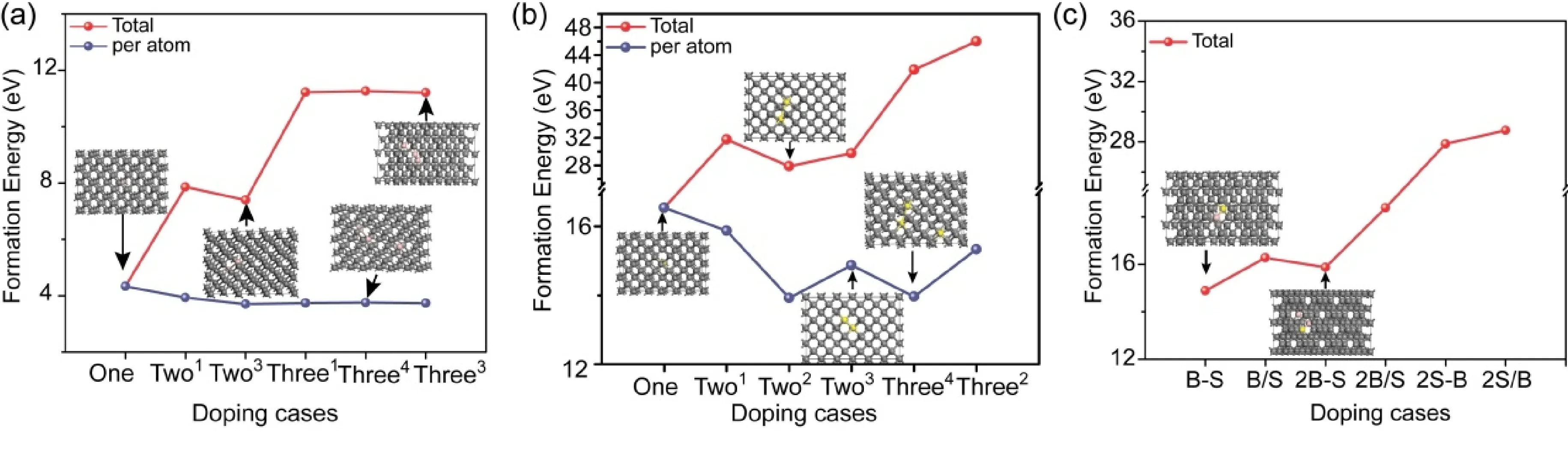
图2 (a)不同比例B掺杂金刚石，(b) S掺杂金刚石和(c) B-S共掺杂金刚石的形成能. 其中(a)和(b)分别给出了平均单个原子掺杂的形成能. 内嵌图为不同比例掺杂后最优化晶胞结构.Fig. 2 Formation energies of diamonds with different B dopings (a), S dopings (b) and co-doping of B and S(c). Average atom formation energies of B or S dopings are also showed in (a) and (b), respectively, while the stabilized crystal structures are also presented.

3.2 B掺杂金刚石电子结构

在不同比例B近邻掺杂金刚石最优化晶体结构基础上，为深入探究掺杂B元素对金刚石性能的影响，进一步计算了其能带及态密度，如图3所示. 由图3(a-b)可以看出，由于B原子较C原子少1个价电子，B替代C后在晶格中引入空穴而使价带顶能级上移并穿越费米面，微弱减小了金刚石的禁带宽度；通过态密度可以看出，掺杂后的价带顶能级主要由C/B-2p轨道贡献，B掺杂未在禁带中形成杂质能级. 由于B原子半径较C原子半径小，因此掺杂后的C-B键键长较C-C键变长并在掺杂位置处发生微小晶格畸变.伴随掺杂后共价键作用的减弱，电子局域性进一步增强，提升了其在其它高对称k点的能级密度[25]. 进一步，当双B原子团簇协同掺杂金刚石晶体后，在缺陷处同时引入一空穴对. 由于双B原子在空间结构上的对称性，较单B原子掺杂，其在禁带中形成一条浅缺陷能级. 双硼原子的近邻掺杂，由于空穴的引入使C-B和B-B键的成键电子发生缺失，从而使C/B-p电子能级向高能量方向移动，进而成为深缺陷能级. 同时，C-B键耦合作用的减弱使掺杂后金刚石价带顶能级进一步弥散，增大载流子有效质量，减弱了载流子迁移率. 当进一步增加掺杂B原子，在金刚石中形成的线性B-B-B排列结构使B及近邻C的2p态重叠进一步加强，中间B电子云向近邻B的移动使其2p态能级在禁带中位置更加局域而促使禁带中杂质能级进一步加深，带隙由1.104 eV增加为1.21 eV，成为电子空穴强复合中心. 此外，由于载流子有效质量决定半导体载流子的迁移率，因此通过调控而获得较小的有效质量，能够进一步提升半导体的电学性能. 我们计算了B掺杂前后金刚石的有效质量，如表2所示. 通过对比可以看出，由于B替位掺杂后新B-C键的形成，其进一步改善了价带顶的能级结构，使空穴有效质量由未掺杂时的0.35 m0减小为0.242 m0(2B)和0.279 m0(3B)，能够有效提升其空穴载流子迁移率[26]，与实验结果吻合较好. 总之，随着替位B掺杂量的增加，易在禁带中产生深缺陷杂质能级.该杂质能级在外电场作用下，可成为载流子跃迁的中间桥梁[20]，而提升金刚石的整体电学性能；另外，空穴有效质量减小利于其空穴迁移率的提升. 总之，B单掺杂会在禁带中产生深缺陷杂质能级，影响金刚石半导体的光学性能但在特定电场条件下利于电学性能提升，但其准确控制掺杂比例尚存在困难.

3.3 S单掺杂金刚石

由于S原子比C原子多2个价电子，单个S原子替代C原子后在晶格中引入了两个自由电子，易造成费米能级上移至导带底附近并伴随在导带底附近形成新的浅缺陷杂质能级[27]，与氮掺杂类似，使金刚石由p型半导体转变为n型半导体，如图4a和图1d所示. 在晶格中引入的富余电子被晶格所共享，进而利于提升掺杂后金刚石的载流子迁移率[28]. 通过对应的PDOS图(图4b)可以看出，由于硫所提供的富余2p电子未与紧邻C原子成键而使其弥散于费米面附近，展宽导带底能级的同时有效降低禁带宽度；对于价带顶能级，C-S成键轨道与C-C成键类似，形貌基本保持不变. 进一步增加近邻S原子掺杂，由于富余电子的进一步掺入，两条新的杂质能级进一步填充在禁带中，如图4(c)所示. 由图4(d)可以看出，由于C-S-S-C结构的产生，S原子的未成键电子为S-C共享，该未成键电子所形成的杂质能级使电子更易跃迁至导带底，从而大幅提升金刚石的导电性能. 虽然进一步远距离掺杂S原子能够进一步提升禁带中杂质能级的密度(图4e)，但其只是进一步加密杂质能级数量并与近邻掺杂相似. 总之，S元素的掺杂，由于在晶格中引入富余电子，从而使金刚石由p型半导体变为n型半导体，同时大幅提升载流子浓度而提升其导电效率，与实验结果吻合较好. 然而，由于S的大剂量掺入易引起晶格畸变，不利于保持金刚石的机械性能，因此小剂量S与B的协同掺杂有望在保持其机械性能基础上获得n型半导体.

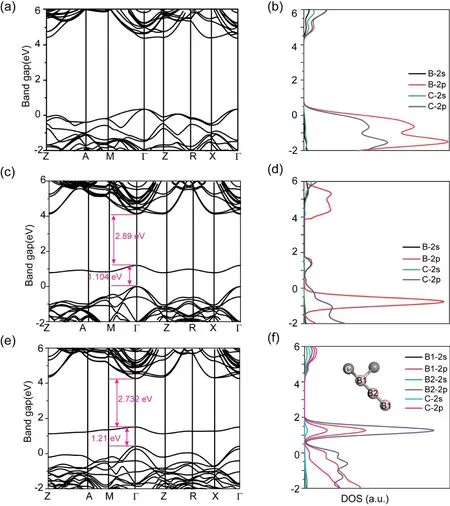
图3 不同比例B掺杂的金刚石电子结构图. (a)和(b)为一个B原子替位C原子后的能带图和态密度图,(c)和(d)为两个B近邻掺杂金刚石的能带图及态密度图,(e)和(f)为三个B近邻掺杂金刚石能带图及态密度.Fig. 3 Electronic structures of diamonds with different B dopings. Band structures and partial densities of states (PDOS) of diamonds with one B atom substituting for one C atom (a-b), two B substituting for two neighboring C atoms (c-d), and three B atoms substituting for three neighboring C atoms (e-f).

表 2 不同元素掺杂后的金刚石电子及空穴有效质量

图4 不同比例S单掺杂金刚石电子机构. (a)和(b)分别为一个S原子替位C原子能带图和分波态密度,(c)和(d)为两个S次近邻掺杂金刚石能带图及态密度,(e)和(f)为两个近邻S与另非近邻S共掺杂金刚石能带图及态密度. 其中(a), (c), (e)中红色给出直线费米面.Fig. 4 Electronic structures of diamonds with different S atoms. Band structures and PDOSs of diamonds with one S atom substituting for one C atom (a-b), two S atoms substituting for two neighboring C atoms (c-d), and third S atoms substituting for the non-neighbor C atoms (e-f). Red lines in (a), (c) and (e) give out the Fermi level.

3.4 B-S协同掺杂金刚石

大量理论和实验证明，通过互异性原子协同掺杂，能够有效克服单元素掺杂存在的弊端. 基于此，我们前期实验通过B-S协同掺杂获得了高电导率的p型半导体金刚石大单晶，并通过调整B、S的掺杂比例实现金刚石从p型向n型的转变. 虽然第一性原理模型所采用的掺杂比例无法与实验完全等同，但不同掺杂比例引起材料性能的变化趋势与实验趋势相同. 基于此，在形成能结果基础上(图2)，我们讨论了三类B/S典型比例近邻掺杂(B∶S=2∶1，B∶S=1∶1和B∶S=1∶2)的电子结构，如图5所示. 由图5及表2可以看出： B-B-S掺杂结构金刚石(B∶S=2∶1)，由于B较C外层少1个价电子，而S较C多2个价电子，因此B-B-S结构协同掺杂未在晶格中掺入富余电子，使掺杂后金刚石保持p型半导体性质；掺杂造成的晶格缺陷使S-2p电子较C-2p电子更加局域，进而贡献并扩宽了导带底能级；掺杂的B原子因为较弱的得电子能力，使B-2p电子主要贡献并扩宽价带顶能级. 两者的共同贡献进一步减小了金刚石的禁带宽度，如图5a-b所示. 进一步增加S掺杂比例为B∶S=1∶1，通过图5c可以看出，B-S原子对的协同掺杂在晶格中引入富余电子而使金刚石实现了由p型向n型的转变(与实验所得负Hall系数相吻合[21]). 由于B原子较小的半径对S原子掺杂所形成的晶格畸变形成了缓冲，共掺杂造成的晶格畸变较S单掺杂小. 较小的晶格畸变及电子掺杂注入使金刚石导带底附近的杂质缺陷能级局域为浅缺陷能级(0.59 eV)，能够明显提升金刚石的电导率. 进一步通过添加S原子而增加富余电子的注入，在金刚石晶格中易形成B-S-S掺杂基团(B∶S=1∶2). 相较于B-S掺杂，一方面，多余电子进入晶格进一步增加了费米面底部杂质能级数量，有望进一步提升载流子的浓度；另一方面，S掺杂进一步造成较大的晶格畸变(图5f)，在价带顶引入一深缺陷能级(0.87 eV)，形成新的捕获中心，不利于电学性能提升. 通过上述不同比例协同掺杂的对比可以看出：B与S同比例掺杂，因为独立电子的存在使金刚石成为n型半导体；当进一步增加B掺杂量，则使金刚石保持p型半导体并呈现与B单掺杂类似的趋势；当进一步增加S掺杂量时，由于晶格畸变的产生使金刚石价带顶产生深缺陷能级，进而影响其电学性能. 因此，调控金刚石由p型向n型转变的最佳阈值比例为B∶S=1∶1. 同时，为保证导带底附近施主能级为浅缺陷能级，n型金刚石半导体的最佳掺杂比例亦应控制为等比例掺杂.我们实验中采用原始投料比作为参照[21]，通过实验中所获得的转变阈值(B∶S=1∶3)与本理论值(B∶S=1∶1)的对比可以看出，S元素在实验过程中发生了析出，从而使实际进入晶格中的数量少于实际投料量，与形成能的计算结果相吻合.

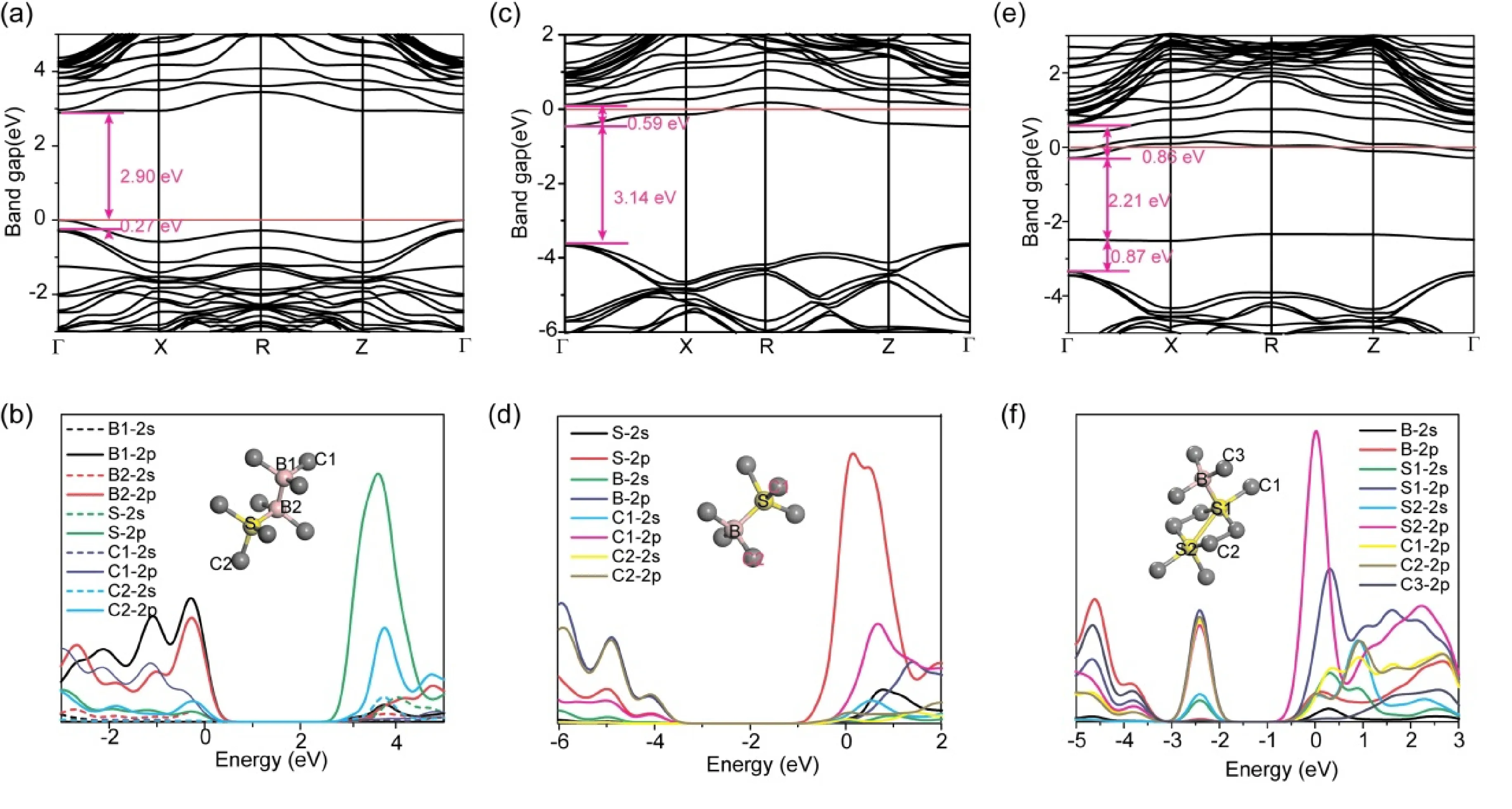
图5 (a)和(b)为B∶S= 2∶1掺杂金刚石的能带及态密度图；(c)和(d)为B∶S = 1∶1掺杂能带及态密度图；(e)和(f) 为B∶S= 1∶2掺杂能带及态密度图. (a)-(c)中红线为费米面位置.Fig. 5 Band structures and PDOSs of diamonds with ratio B∶S= 2∶1 (a-b), B∶S= 1∶1(c-d) and B∶S= 1∶2 (e-f). Red lines in (a)-(c) are Fermi levels.

4 结 论

采用第一性原理，本文主要讨论了不同浓度B和S协同掺杂实现金刚石半导体由p型向n型的转变. 通过形成能的比较得出B元素在金刚石中无掺杂阈值且易团聚；在保证金刚石机械性能条件下，S的掺杂浓度较小. 由电子结构计算得出，B替位掺杂易在晶格中引入空穴，大浓度B掺杂使金刚石保持p型半导体且在价带顶产生深能级缺陷. 该深缺陷能级在特定外电场条件下为载流子提供了跃迁桥梁，利于金刚石电学性能的提升； S掺杂虽在晶格中引入电子，使金刚石转变为n型半导体，但大浓度掺杂所造成的晶格畸变对机械性能影响较大. 相对于其他比例掺杂，B∶S=1∶1协同掺杂在保证小晶格畸变条件下获得n型金刚石半导体且形成能最低，为最可能掺杂方式. 通过实验与理论所得B-S物料比进一步证明实验合成过程中存在S元素的析出现象.