自动翻越式玻璃幕墙清洁机器人设计
2021-12-27卢红煜秦明旺王浩坤李红阳
卢红煜,秦明旺,王浩坤,李红阳
(西南石油大学 工程学院,四川 成都 610500)
0 引言
随着建筑业的发展,出于采光和减质量考虑,越来越多的建筑采用玻璃幕墙作为外墙面,但要维持良好的采光率就需经常对玻璃幕墙进行清洁[1-2]。高空作业“蜘蛛人”存在极大安全隐患(图1),而目前市场上现有自动擦窗机普遍是单一平面作业,依靠吸盘或者导轨实现运动,作业范围窄,需不断通过人工更换作业面,才能实现大范围清洁,特别是对于在中间有钢结构的玻璃以及建筑物转角处,现有技术基本没法处理[3-5]。基于此,本文设计一款可自动越障的玻璃幕墙清洁机器人,不仅能够达到传统玻璃墙清洗机的清洗效果,还能实现外墙之间自动翻面和跨越障碍的功能,高效、可靠地完成清洁工作。

图1 “蜘蛛人”和现有擦窗机器人
1 清洁机器人整体结构设计
清洁机器人整体结构如图2所示,主要由吸附系统、行走运动系统、玻璃清洗系统组成,将履带式行走机构与真空吸附腔体设计为一体,极大地简化了结构,从而减轻了机器人自质量。机器人的直线运动采用履带式行走机构,有效增大机器人与玻璃面的驱动接触面积和摩擦力,以防在玻璃面上打滑[6-7]。机器人在垂直壁面工作时,其真空吸附力尤为重要,为减少泄漏量,在真空吸附腔体底部设有密封裙。同时,设计选用微型负压传感器实现真空吸盘内的负压监测。清洁机器人越障作业如图3所示,通过解除接近障碍物的真空箱体的负压,使其通过雪橇状的弧形条直接越过障碍物,擦拭装置直接通过转动弹簧回复原位。翻面作业如图4所示,当遇到转角时,通过舵机抬起前端机架,前进至机架可以吸附在另一工作面上。当吸附稳定后,再抬起后端机架缓慢前进从而完成整个换面动作。

1—擦拭装置;2—连接架;3—机架;4—移动体;5—舵机。图2 清洁机器人整体结构

图3 越障作业示意图

图4 翻面作业示意图
2 静力学计算分析
在清洗状态下擦窗机器人仅在Oxy平面进行直线和转向运动。当机器人静止吸附于玻璃上时,履带被制动,故仅考虑机器人与壁面间相对滑动。
2.1 清洁状态下真空吸附力的计算
图5为履带式运动状态下机器人沿y轴方向运动时的静力学受力分析图,下面对这种情况进行受力分析。

图5 直线运动静力学受力分析图
图5中:Ni为各接触部分的支持力,i=1,2,3,4,5;fi为各接触部分的摩擦力,i=1,2,3,4,5;FP为单个吸盘吸附力;h为机器人质心与玻璃壁面间距离;l为相邻真空腔体间的距离;G为擦窗机器人自身重力。根据摩擦特性:
(f1+f2+f3+f4+f5)-G=0
(1)
此时垂直壁面和平行壁面的受力需满足:
3FP-(Ν1+Ν2+Ν3+Ν4+Ν5)=0
(2)
所受平衡力矩为
FPl+2FPl+3FPl-N4l-2N3l-3N2l-4N1l-Gh=0
(3)
设密封条与玻璃壁面间的摩擦系数为μ1;履带与玻璃壁面间的摩擦系数为μ2;清洁刷与玻璃壁面间的摩擦系数为μs。由对称性可简化计算,取N2=N3=N4=N。则有:
f1=μsΝ1;f5=μsΝ5
(4)
f2=f3=f4=μ1Ν+μ2Ν=(μ1+μ2)Ν
(5)
联立式(1)-式(5)得吸盘吸附力:
(6)
支持力:
(7)
为避免机器人从玻璃壁面倾翻落下,在颠覆力矩作用下,应满足Νi≥0,即有
(8)
引入安全系数k,联立式(6)和式(8)得吸盘吸附力范围
(9)
实际工作中,清洁刷与玻璃壁面间摩擦力可忽略不计[8],则有
(10)
由机器人主要参数可得:h=110 mm,l=710 mm,m=5 kg;取重力加速度g=9.8 m/s2,摩擦系数μ1=0.25,μ2=0.20;安全系数k=2。由式(10)得
FP≥2×Max{36.30 N;7.59 N}=72.6 N
因此,此处取吸盘吸附力FP=100 N。
2.2 翻面作业时真空吸附力的计算
图6为清洁机器人翻面时静力学受力分析图。机器人通过舵机使前清洁盘和前两个真空吸附腔体向上抬起,由第三个真空吸附腔体向前运动从而跨越障碍物或完成换面工作。

图6 翻面作业静力学受力分析
图6中:N为玻璃壁面对真空腔体的支持力;Νs为玻璃壁面对清洁盘的支持力;Fpm为吸盘吸附力;l为吸盘中心与清洁盘间距离;f为玻璃壁面对腔体的摩擦力;fs为玻璃壁面对清洁盘的摩擦力;H为质心到玻璃壁面的距离;G为机器人自身重力。由机器人不发生滑落和倾覆的临界平衡方程
∑Fy=0;∑Fz=0;∑MA=0
(11)
得
(12)
密封条材料与玻璃壁面间的摩擦系数为μ1;清洁刷与玻璃壁面间的摩擦系数为μs,得
f=μ1Ν+μ2Ν;fs=μsΝs
(13)
联立式(12)、式(13)得吸盘吸附力:
(14)
支持力:
(15)
要使机器人在玻璃壁面可靠吸附,需满足
(16)
引入安全系数k,并联立式(14)、式(16),得吸盘吸附力范围:
(17)
由机器人实际尺寸及参数得:H=1 000 mm;l=710 mm;m=5 kg;取重力加速度g=9.8 kg/s2;摩擦系数μ1=0.25;μ2=0.20;μs=0.10;安全系数k=2。
由式(17)得
Fpm=2×Max{165.57 N;69 N}=325.14 N。
因此,此处取Fpm=350 N。
由以上计算分析可得:擦窗机器人直线运动状态下吸盘吸附力可取100 N;转向状态下吸盘吸附力应达到350 N。
3 真空箱体可行性分析
真空箱体的密封性能是保证吸附结构正常使用的前提,为此根据清洁机器人作业时的不同工况分析箱体的密封性能。密封条橡胶是实现真空箱体密封性能的主要元件,本文选择Mooney-Rivlin模型来表征橡胶的超弹性本构模型。
3.1 Mooney-Rivlin模型
常用的Mooney-Rivlin模型的应变能可以表示为
(18)
式中:W为应变能密度;Cij为 Rivlin系数;I1、I2分别为第一、第二Green应变不变量。
一般近似认为橡胶材料不可压缩,按Mooney-Rivlin方程的简化形式,提取前两项,则应变能表示为
W=C10(I1-3)+C01(I2-3)
(19)
由kirchhoff应力张量tij和Green应变张量γij之间的关系得
(20)
橡胶材料主应力与其主伸长比之间的关系为
(21)

(22)
将两参数的Mooney-Rivlin方程代入上式,有
(23)
真实应力t1和工程应力t=γσ,因此,得出工程应力与应变关系为
(24)
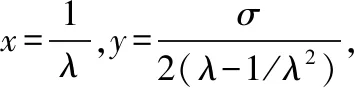
3.2 真空箱体有限元模型建立
真空箱体采用304不锈钢材料,其参数如表1所示。

表1 箱体材料性能参数
根据箱体橡胶的工作特点,真空箱体简化后结构如图7所示。

图7 箱体简化后真空箱体三维模型图
密封条为橡胶材料,采用Mooney-Rivlin超弹本构对其定义,其模型系数C10=1.1,C01=-0.3,D1=0,近似为不可压缩材料,材料拉断伸长率为650%。模型网格划分:箱体采用六面体线性缩减积分C3D8R单元,密封条采用六面体线性杂交C3D8H单元,网格模型如图8所示。

图8 箱体网络模型
边界条件设置如下:将基地板下表面完全固定,密封条与箱体实施绑定约束,真空箱体内的真空度通过改变箱体内外表面的压力实现。实际工况中,清洁机器人在玻璃上移动,根据橡胶与玻璃之间的摩擦系数,在接触属性中通过罚函数定义摩擦系数为0.25。
3.3 密封条密封与失效分析
针对小型清洁机器人真空度在10~40 kPa范围内,本节对不同真空度下密封条的接触应力和Mises应力进行对比分析,研究真空度对密封条力学性能的影响规律。密封条密封性能是评价真空箱体性能的主要依据,取不同真空度下密封条与基地板的接触应力结果如图9和图10所示。

图9 不同真空度下密封条接触应力云图
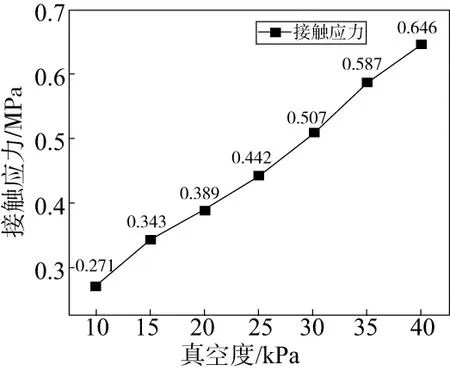
图10 不同真空度时密封条接触应力曲线
从图9可知,密封条接触应力较大值主要集中在箱体接触边缘,边缘两侧的接触应力较小,真空箱体与密封条接触区域的正下方起主要密封作用,故该区域接触应力最大。从图10可知,随着真空度变大,密封条接触应力也随之变大,相应地其密封性能也逐渐增强。当真空度为40 kPa时,密封条的接触应力最大为0.646 MPa。
相应的Mises应力是评价密封条是否失效的另一指标。为了判断不同真空度下系统的强度,分别计算了不同真空度下密封条的应力值,其计算结果如图11和图12所示。

图11 不同真空度下密封条Mises应力云图

图12 不同真空度下密封条Mises应力曲线
由图11可知,密封条应力主要集中在两侧边缘处。因密封条在箱体的挤压下发生变形,一部分橡胶被挤压到边缘,从而导致应力变大。当挤压力过大时,密封条将在边缘处发生溃烂。根据图12可知,随着真空度的增大,密封条的Mises应力随之增大,最大值为0.364 MPa,未超过橡胶材料的强度极限,故真空箱体在实际工作中密封条不会发生失效。
3.4 清洁状态下密封条密封性能分析
针对真空箱体移动时对密封条进行动态分析。根据实际清洁机器人移动速度,设置真空箱体的速度为4.42 m/min,分别计算真空度为10 kPa、20 kPa、30 kPa以及40 kPa下密封条的接触应力,选取密封条上4点绘制接触应力曲线如图13所示。
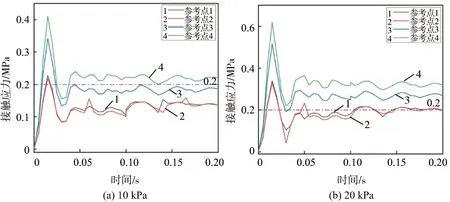
图13 移动时密封条在不同真空度的接触应力曲线
动态分析分为抽真空和移动两个过程,0~0.1 s为抽真空加载过程,0.1~0.2 s为真空箱体移动阶段。当接触应力<0.2 MPa时,密封条的密封性能较差,无法保证箱体的正常移动。从图13可知,当真空度<20 kPa时,密封条上有些部位的接触应力<0.2 MPa,不能满足箱体正常移动的要求,故机器人在完成清洁作业的时候真空度应超过20 kPa。
3.5 翻面作业时密封条密封性能分析
越障作业时,只有一个真空箱体支撑整个机器质量,且还需额外承受一个弯矩作用,故对接触应力较小的一侧进行密封性能分析。从图14可知,当真空度为10 kPa时,因真空箱体提供的吸力不足,翻转作业时,密封条上有些部位的接触应力为0,说明此时密封条与基地板不再接触,实际作业中不允许发生。
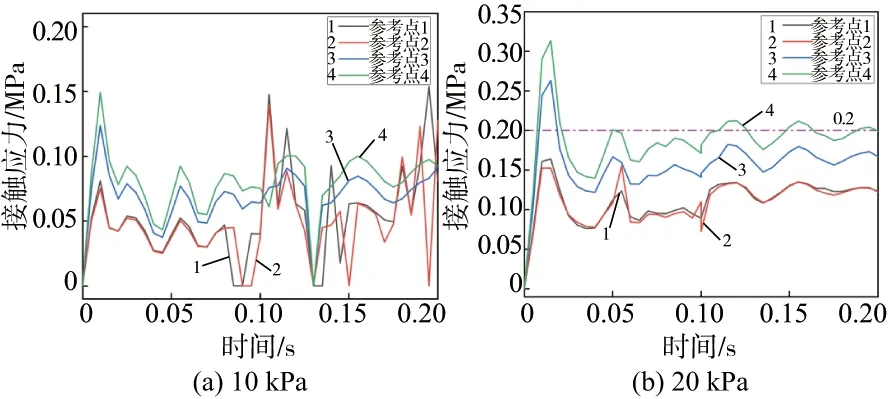
图14 翻转时密封条在不同真空度的接触应力曲线
随着真空度的增大,当真空度超过10 kPa后密封条与基地板一直保持接触状态。但为了保证机器人工作时的可靠性,应该以密封条的接触应力大小来评判其接触性能。当真空度为40 kPa时,翻转作业过程,密封条的接触应力都>0.2 MPa,说明此时密封条的密封性能较好。最后计算得到当真空度为35 kPa时,密封条的接触应力就已经超过0.2 MPa,故实际机器人在翻转作业过程中真空度的区间范围为35~40 kPa。
4 结语
本文设计了一款可自动翻越式玻璃幕墙清洁机器人,可实现自动翻面和越障功能。对清洁机器人各状态进行了力学和运动学的相关计算分析,得出理论所需最小吸附力、实际转向的半径以及需要克服的阻力矩、关键部件的安全系数等,并对其最关键部位真空箱体进行可行性分析,利用静态力学分析与动态显示分析求解得到密封条在不同工况下的接触应力与Mises应力,得到以下结论:
1)密封条的接触应力和Mises应力随着真空度的增大而增大,当真空度达到最大值时,密封条材料不会发生失效;
2)在清洁作业过程中,真空箱体的真空度应超过20 kPa;
3)在翻转作业中,真空箱体的真空度区间应在35~40 kPa范围内选取。
