单齿轮副面齿轮分扭传动机构的接触斑点分析研究
2021-12-27李科攀刘李叶佩佩靳广虎
李科攀,刘李,叶佩佩,靳广虎
(1.南京航空航天大学 直升机传动技术试验室,江苏 南京 210016;2.中国航空发动机集团有限公司 湖南动力机械研究所,湖南 株洲 412002)
0 引言
面齿轮传动具有传动比大、可靠性高和结构紧凑等诸多优点,在航空、船舶等高速、重载机械传动领域具有良好的应用前景。美国军方已将面齿轮应用于直升机主减速器中。LITVIN F L等[1-2]研究了面齿轮的齿面方程、齿宽特征和接触分析;谭武中等[3]分析了面齿轮在直升机传动系统中的应用前景;汪中厚等[4]研究了正交面齿轮副的接触斑点及传递误差。
在面齿轮分扭传动机构方面,BOSSLER R B[5]提出了一种具有两个功率提取路径传递转矩的齿轮装置。赵宁等[6]分析了同轴面齿轮传动系统的静态均载特性;在面齿轮制造方面,王延忠等[7]提出使用蝶形刀具通过磨削的方式来加工面齿轮;唐进元团队[8]提出了面齿轮的插铣加工及刨削加工。
由上述分析可知,对于传动系统中同时包含多个面齿轮副且考虑承载变形的接触特性影响因素的研究尚且欠缺。因此,本文首先根据受力分析了机构中的承载变形;建立了包含承载变形的面齿轮副接触轨迹方程;获得了承载变形对接触斑点在面齿轮齿面上位置的影响规律;并通过有限元分析对该理论方法进行了验证。
1 传动机构的承载变形分析
在图1中,动力通常由圆柱齿轮输入,并将功率分流至两个面齿轮。然而,由圆柱齿轮流向两个面齿轮的功率往往不均等,从而影响到面齿轮的接触,并最终影响系统的寿命。为分析载荷分配对上下两个面齿轮副接触斑点的影响,需要对机构中的受力情况进行分析。
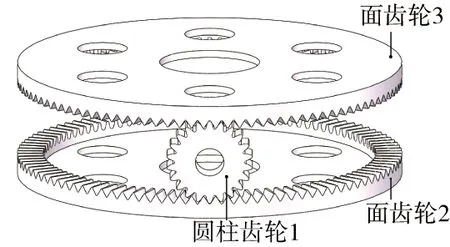
图1 单齿轮副分扭传动机构模型
如图2所示,将啮合力分解,获得面齿轮的轴向力和切向力。对面齿轮2,两个分别为Fz21和Fx21,面齿轮3则为Fz31和Fx31。面齿轮2和面齿轮3相应于圆柱齿轮的反作用力分别为Fy12、Fx12、Fy13和Fx13。
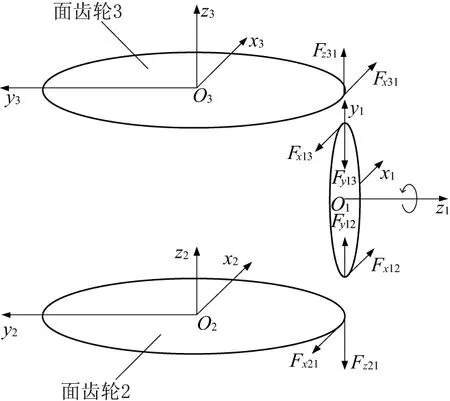
图2 传动机构的受力分析示意图
根据理论力学中力的平移理论,作用在刚体上的力可以平移到任一点,但必须附加一个力偶,使力偶矩等于原力对新作用点之矩。如图3所示,以圆柱齿轮为研究对象,当Fy12和Fy13不能在y1方向平衡时,圆柱齿轮1的支撑轴将在y1方向产生径向变形ay1;同时,圆柱齿轮1的支撑轴受到(Fy12-Fy13)引起的弯矩My1作用,会在y1z1平面内产生弯曲变形by1。同样,Fx12和Fx13不能在x1方向平衡时,圆柱齿轮1的支撑轴将在x1方向上产生径向变形ax1,此时在(Fx12-Fx13)引起的弯矩Mx1的作用下,圆柱齿轮1的支撑轴会在x1z1平面内产生弯曲变形bx1。在驱动转矩T1和反作用转矩(Fx12+Fx13)r1的作用下,小齿轮的支撑轴会产生扭转变形s1。
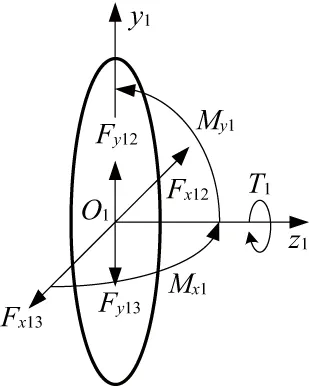
图3 圆柱齿轮力的简化示意图
如图4所示,以面齿轮2为研究对象,切向力Fx21使得面齿轮2的支撑轴在x2方向上产生径向变形ax21;在切向力Fx21产生的弯矩Mx2的作用下,面齿轮2的支撑轴会在x2z2平面内产生扭转变形bx21;在轴向力Fz21的作用下,面齿轮2的支撑轴会在z2方向上产生轴向变形az2,同时轴向力Fz21会在y2z2平面内产生弯矩Mz2,并在y2z2平面内使得面齿轮轴线产生倾转角变形bz21。此外,支撑轴还存在扭转变形s2。

图4 面齿轮力的简化示意图
2 包含承载变形的齿面接触轨迹方程
根据已有研究成果[9],可将各项承载变形转换为安装误差。如图5和图6所示,假设圆柱齿轮和面齿轮无承载变形时的坐标系分别为Sgc和Sfc,有承载变形发生的坐标系分别为Sgc′和Sfc′。那么通过坐标转换可以得到对于两个坐标系之间的转换关系。
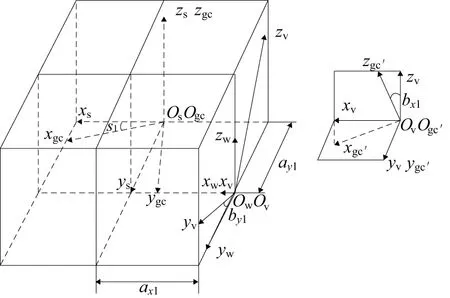
图5 圆柱齿轮变形量的转化
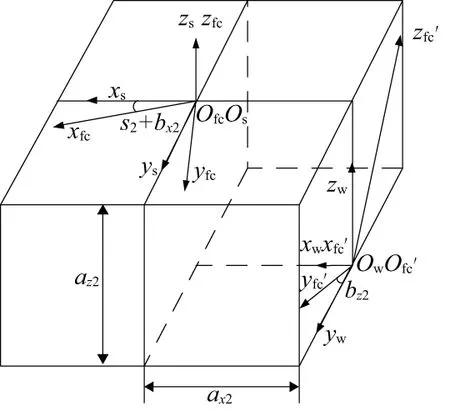
图6 面齿轮变形量的转化
在圆柱齿轮坐标系Sg中,圆柱齿轮的齿面∑g和面齿轮的齿面∑f在接触点处应有相同的位置向量和法线向量,其在数学上的表达式为
(1)
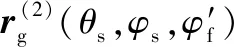
(2)
式中:Mgc,f为面齿轮与圆柱齿轮之间的坐标转换矩阵;Agc,f为Mgc,f前三行、前三列所组成的子矩阵。将式(2)代入式(1)中可获得包含变形量的面齿轮副啮合点应满足的方程,即
(3)
式中:rgx(1)、rgy(1)、rgz(1)和rgx(2)、rgy(2)、rgz(2)分别表示rg(1)和rg(2)的分量;ngx(1)、ngy(1)、ngz(1)和ngx(2)、ngy(2)、ngz(2)分别表示ng(1)和ng(2)的分量。求解式(3)可获得面齿轮齿面方程中的参数θs和φs,带入到面齿轮齿面方程即可获得面齿轮齿面上的接触点。
3 承载变形对接触斑点的影响
根据弹性体的接触理论以及点接触面齿轮副中的齿面几何特性,可获得圆柱齿轮与面齿轮啮合副齿面接触点处的接触椭圆的长、短半轴的计算公式为
(4)
式中:μ1、E1和μ2、E2分别为圆柱齿轮和面齿轮材料的泊松比、弹性模量;K11、K12和K21、K22分别为圆柱齿轮和面齿轮在啮合点处的主曲率;u和v为椭圆积分函数,可根据求得的τ数值查椭圆积分系数表[10]获得。参数τ为
(5)
根据以上理论,对系统中的接触椭圆进行计算,本文所使用的参数如表1所示。
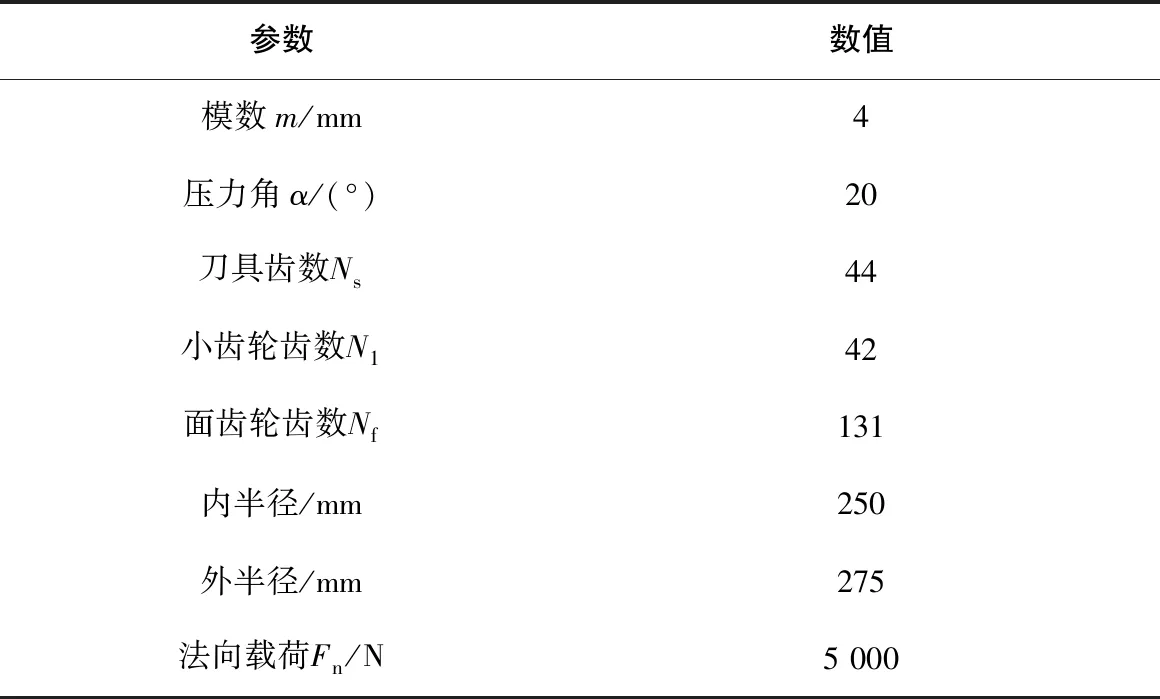
表1 系统的结构参数
定义面齿轮2处和面齿轮3处的面齿轮副分别为面齿轮副2和齿轮副3。为研究承载变形对机构中每个面齿轮副接触斑点的影响,分别计算了圆柱齿轮承载变形(包括ax1、ay1、bx1、by1和s1)和面齿轮承载变形(包括ax21、az2、bz21、bx21和s2)对各面齿轮副接触椭圆的影响。计算结果如图7-图9所示;数据统计结果如表2-表4所示。表中最后一行表示无变形时接触斑点中心在面齿轮齿面上的原始位置。
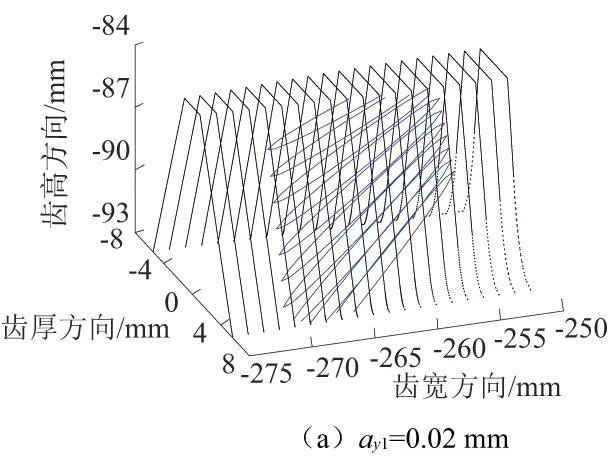
图7 圆柱齿轮变形对面齿轮副2接触斑点的影响
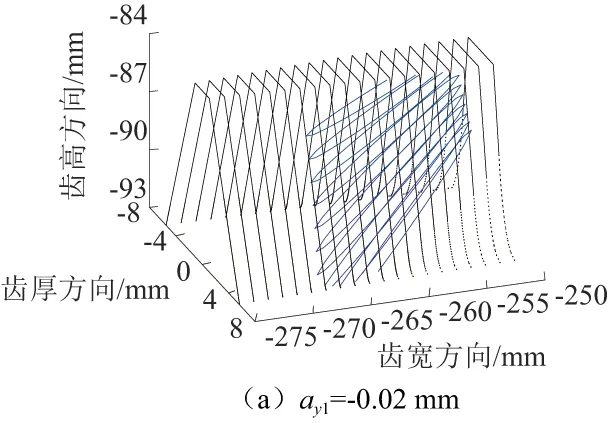
图8 圆柱齿轮变形对面齿轮副3接触斑点的影响
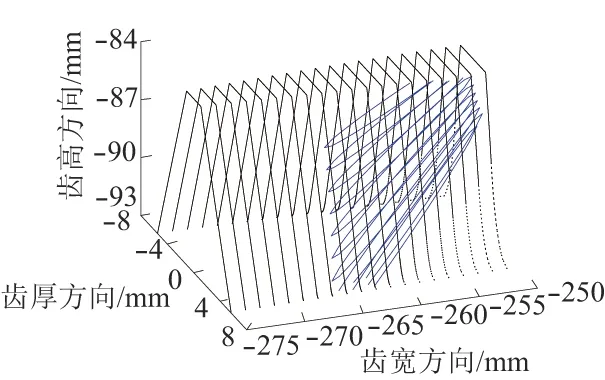
图9 面齿轮2变形bz21对面齿轮副2接触斑点的影响
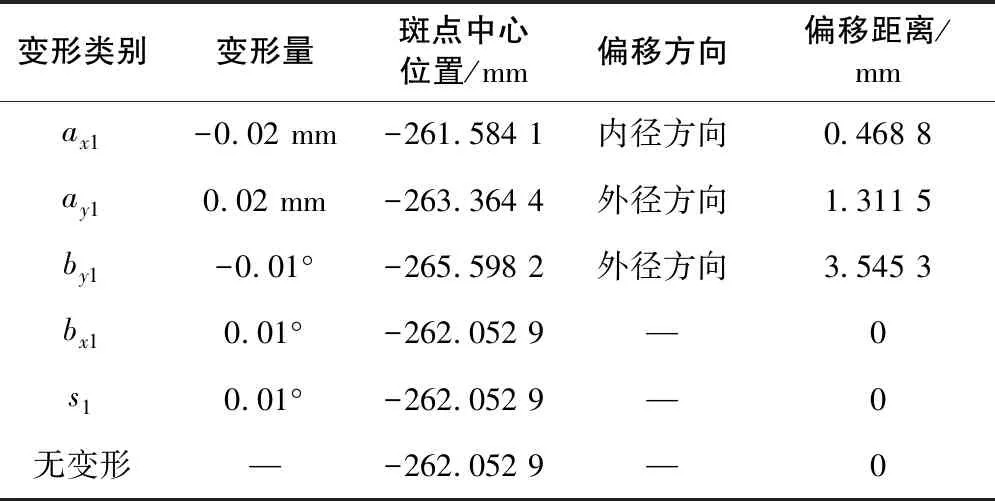
表2 圆柱齿轮变形对面齿轮副2接触斑点位置的影响
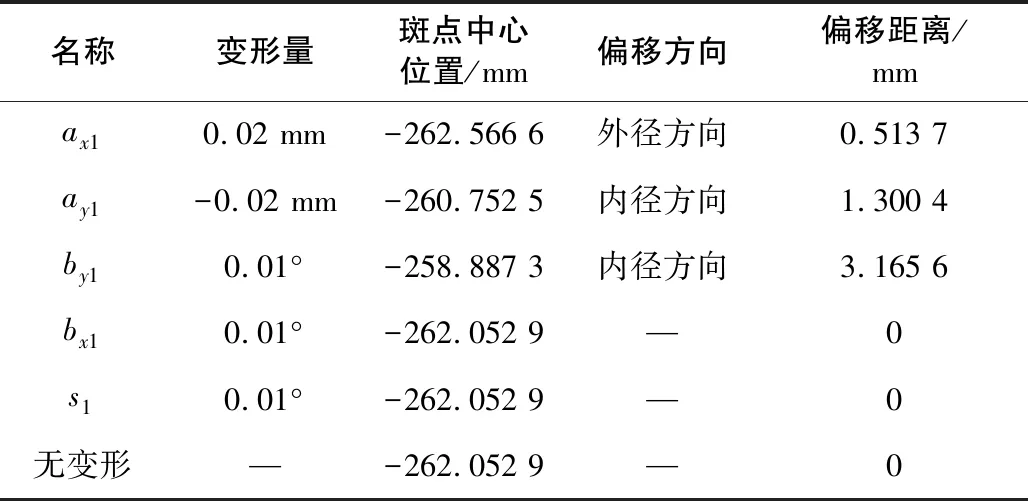
表3 圆柱齿轮变形对面齿轮副3接触斑点位置的影响
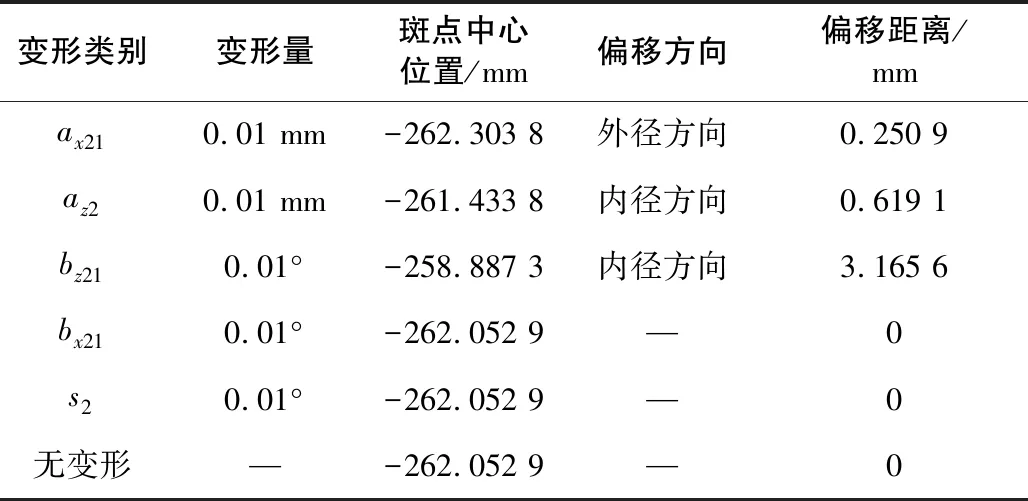
表4 面齿轮2变形对面齿轮副2接触斑点位置的影响
根据图7-图9和表2-表4可知:
1)面齿轮齿面上接触斑点的长轴远大于短轴,接触斑点近似为沿长轴方向的线段,接触斑点的方向为由内半径的齿顶指向外半径的齿根。
2)圆柱齿轮和面齿轮的承载变形使接触斑点在齿面上的位置发生改变。对于面齿轮副2,使接触斑点沿面齿轮2齿面向内半径方向移动的有ax1、az2和bz21,使接触斑点向外径方向移动的有ay1、by1和ax21;对于面齿轮副3,使接触斑点沿面齿轮3齿面向内半径方向移动的有ay1、by1、az2和bz21;使接触斑点向外径方向移动的有ax1和ax21;其他变形量对接触椭圆的位置基本无影响。
4 有限元验证
为验证接触斑点理论分析的有效性,通过Ansys分析软件对系统的接触进行仿真。有限元模型如图10所示。对圆柱齿轮施加转矩2 500 Nm。
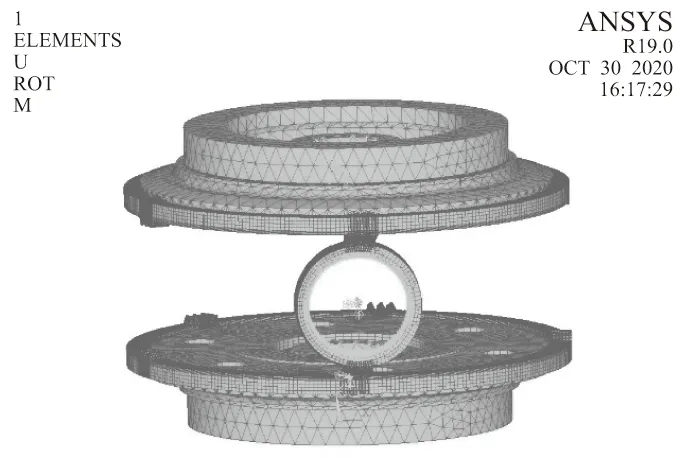
图10 分扭传动系统网格划分结果
图11为有限元分析结果。由图可见,接触域中心的连线为斜线(接触椭圆的长轴)指向内径的齿顶;接触椭圆的长轴远大于短轴。这与理论分析获得的接触椭圆分布趋势以及接触椭圆长、短半轴尺寸之间的关系一致,间接验证了理论分析的有效性。
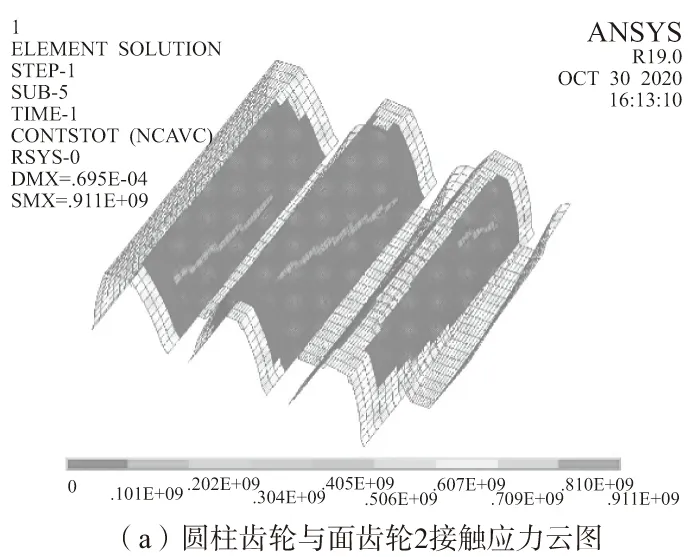
图11 圆柱齿轮与面齿轮啮合齿面的接触应力云图
5 结语
1)单齿轮副面齿轮分扭传动机构两支路的啮合力会使圆柱齿轮与面齿轮的空间相对位置发生改变,使接触斑点偏离理想接触位置;
2)由于两个面齿轮的空间位置以及面齿轮副间的承载力差异,相对于两个面齿轮来说,圆柱齿轮的承载变形分为正值和负值,因此对两面齿轮齿面接触椭圆位置的影响正好相反;圆柱齿轮与面齿轮副齿面接触椭圆对两齿轮轴线夹角的变化最敏感;
3)为降低承载变形对接触斑点位置造成的影响,使机构中的各个面齿轮副都具有良好的接触效果,应采取调整措施使两支路载荷尽量均等,使接触斑点位于面齿轮齿面中部,以延长机构的使用寿命。
