星轮支承刚度对两级星型齿轮传动系统均载特性的影响

吕世恒，李政民卿

(南京航空航天大学 机电学院，江苏 南京 210016)

0 引言

星型齿轮传动系统因具有功率分流、结构紧凑、承载能力高等优点，在航空、船舶等传动领域应用较为广泛[1]。星型轮间载荷分配的均匀性是考量星型齿轮传动系统性能的重要因素，因此开展星型齿轮传动系统的均载特性研究具有重要意义。

目前，国内外学者对星型齿轮传动系统均载特性已经开展了大量研究。孙振宇等[2]研究了齿轮误差对系统静态均载的影响规律；袁擎宇、鲍和云等[3-5]建立了不考虑星轮横向振动的两级星型齿轮传动系统均载分析模型，分析了综合误差对系统均载的影响规律；宁凤莲[6]开展了两级星型齿轮传动系统的均载测试试验研究；MO S等[7-8]研究了工况、误差以及浮动量等对两级星型齿轮传动系统均载特性的影响，并开展了均载测试试验研究。国内外学者已针对误差、中心轮支承刚度以及浮动量等因素开展了大量的研究；但在大部分的均载分析模型中，存在双联星轮处的支撑刚度足够大的假设，忽略了双联星轮的横向振动对系统均载特性的影响。

因此，本文以两级星型传动系统为研究对象，根据平移与扭转变形的变形协调关系，提出了双联齿轮弯扭耦合振动边界条件，建立了考虑双联星轮横向振动的弯扭耦合动力学模型，分析了星轮支承刚度对系统均载特性的影响规律，为两级星型齿轮传动系统支承结构的设计提供了理论支撑。

1 两级星型齿轮传动系统

两级星型齿轮传动系统结构，如图1所示。其中太阳轮Z1为输入轮，星型轮Z2与星型轮Z3为双联齿轮，它们以太阳轮为中心均匀分布；内齿圈Z4为输出轮，与太阳轮Z1同轴。输入功率经由太阳轮Z1分流给N个星型轮Z2，又经过星型轮Z3汇流到内齿圈Z4输出。

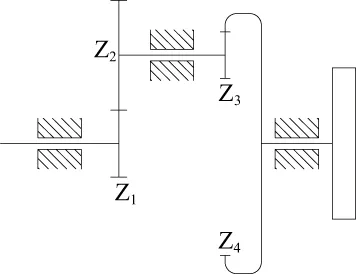
图1 两级星型齿轮结构示意图

2 两级星型齿轮传动系统动力学建模

2.1 双联齿轮弯扭耦合振动边界条件

在两级星型齿轮传动系统中，由于内外齿轮副啮合线为两条空间异面直线，使得双联星轮两端受到不同方向的力，产生了复杂的空间运动。因此，在以往的两级星型传动系统动力学模型中，通常假设双联星轮支承刚度很大，忽略了星轮的横向位移以简化建模过程。为考虑双联星轮横向振动对系统动力学的影响，本文根据平移与扭转变形的变形协调关系，将双联齿轮横向振动当量为扭转振动，形成双联齿轮弯扭耦合边界条件：

θeq=x/rb

(1)

式中：θeq为星轮当量扭转角；x为星轮弯曲振动位移量；rb为星轮基圆半径。

根据星型齿轮传动系统实际结构绘制双联齿轮静态受力图，如图2所示。

图2 双联齿轮静态受力图

根据图示结构，利用材料力学应变能计算方法，计算双联齿轮弯曲与扭转变形时的应变能，并结合应变能等量关系，形成当量扭转刚度的计算方法：

(2)

式中：keq为双联轴当量扭转刚度；θAst、θDst分别为双联轴两端齿轮受静态力时扭转角；xAst、xDst分别为双联轴两端齿轮受静态力时沿啮合线方向的位移；kr为双联轴扭转刚度；FA为星型轮Z2所承受的合力；FD为星型轮Z3所承受的合力，rb2、rb3分别为星型轮Z2与星型轮Z3的基圆半径。

2.2 两级星型齿轮传动系统弯扭耦合动力学模型

将两级星型齿轮传动系统简化得到系统等效力学模型，如图3所示。在简化模型中将星型齿轮机构的各构件均看作刚体，并且太阳轮Z1、内齿圈Z4、两级星型齿轮(Z2i、Z3i)为基本浮动构件。啮合副处及支承处的弹性变形用等效弹簧刚度表示，图中K1-2i表示太阳轮与星型轮Z2之间的轮齿啮合刚度，K4-3i表示内齿圈与星型轮Z3之间的轮齿啮合刚度；Kx1(Ky1)和Kx4(Ky4)分别表示太阳轮Z1与内齿圈Z4支承处横向(纵向)的等效弹簧刚度。其中K2i表示星型轮Z2在啮合线方向的等效支承刚度，K3i表示星型轮Z3在啮合线方向的等效支承刚度，Ki表示双联齿轮轴的扭转刚度。此系统共有(6+4N)个自由度，其广义坐标如下：

图3 星型齿轮传动系统等效动力学模型

X=[θ1,x1,y1,θ2i,θ3i,x2i,x3i,θ4,x4,y4]T。

其中：θ1为太阳轮扭转的微转角；x1为太阳轮中心横向微位移；y1为太阳轮中心纵向微位移；θ2i为第一级第i个星型轮扭转的微转角；θ3i为第二级第i个星型轮扭转的微转角；x2i为第一级第i个星型轮中心的啮合线方向微位移；x3i为第二级第i个星型轮中心的啮合线方向微位移；θ4为内齿圈扭转的微转角；x4为内齿圈中心横向微位移；y4为内齿圈中心横向微位移；本文中下标i表示不同支路(i=1,2,3)。

2.3 系统运动微分方程

根据系统结构布置位置，由几何分析可得如下啮合线方向的位移：

式中：rb1为太阳轮的基圆半径；rb2、rb3分别为星型轮Z2、星型轮Z3的基圆半径；rb4为内齿圈的基圆半径；αw、αN分别表示外啮合齿轮副与内啮合齿轮副的啮合角；xn1-2i、xn4-3i分别表示外、内齿轮副沿啮合线方向的位移；e1-2i、e4-3i分别表示外、内齿轮副间的准静态传递误差。

根据上述啮合线位移分析，易得各齿轮副间的动态啮合力为

(4)

式中：Fd1-2i、Fd4-3i分别表示外、内齿轮副间的动态啮合力；c、k分别表示齿轮副间等效阻尼与等效弹簧刚度。

根据2.2节中系统动力学模型可推得系统运动微分方程：

(5)

式中：I1、I2i分别为太阳轮与星型轮Z2的转动惯量；I3i、I4分别为星型轮Z3与内齿圈的转动惯量；m1、m2i分别为太阳轮与星型轮Z2的质量；m3i、m4分别为星型轮Z3与内齿圈的质量；T1为太阳轮的驱动转矩；T2为内齿圈的负载转矩。

3 均载特性分析

3.1 均载系数计算方法

在两级星型齿轮传动系统中，存在多支路分汇流结构，各支路间载荷分配的均衡性直接影响系统的工作性能与寿命。通常采用均载系数表征传动系统的不同支路间载荷分配的均匀性。本文给出两级星型齿轮传动系统均载系数定义如下：

(6)

式中：ΩW(ΩN)表示系统外(内)齿轮副均载系数；CdWi(CdNi)表示第i支路外(内)齿轮副动态啮合力的均方根值；np表示两级星型齿轮系统总支路数。

3.2 不同均载分析模型对比分析

为研究星轮横向振动对系统均载的影响，本文以两级星型齿轮传动系统为研究对象，分别利用未考虑星轮横向振动以及考虑星轮横向振动的均载分析模型，开展系统均载特性分析。具体系统参数如表1所示。

表1 两级星型齿轮系统基本参数

根据系统基本参数，以准静态传递误差为动力学激励[9]，利用龙格库塔法，开展系统响应分析，获得两种模型下系统各支路的动态啮合力，如图4所示。其中线1表示第1支路动态啮合力，线2表示第2支路动态啮合力，线3表示第3支路动态啮合力(本刊为黑白印刷，如有疑问请咨询作者)。

图4 系统各支路的动态啮合力时域图

由上述分析可知，两种均载模型所计算的动态啮合力变化规律一致，证明了本文所提出的均载分析模型具有合理性。其中值得注意的是，在未考虑星轮横向振动的均载分析模型中，外齿轮副的均载系数为1.059，内齿轮副的均载系数为1.042；而在考虑星轮横向振动的均载分析模型中，外齿轮副的均载系数为1.045，内齿轮副的均载系数为1.034，其结果均小于未考虑星轮横向振动的均载分析模型。这主要是因为在未考虑星轮横向振动的均载分析模型中存在星轮支承刚度无穷大的假设，星轮无法自由浮动，进而无法补偿由于制造、安装和受载变形等因素引起的各类误差，导致均载分析结果偏大。

3.3 星轮支承刚度对系统均载特性的影响规律研究

根据系统基本参数，取双联星轮的支承刚度连续变化，开展星轮支承刚度对系统均载特性的影响规律研究，分析结果如图5所示。

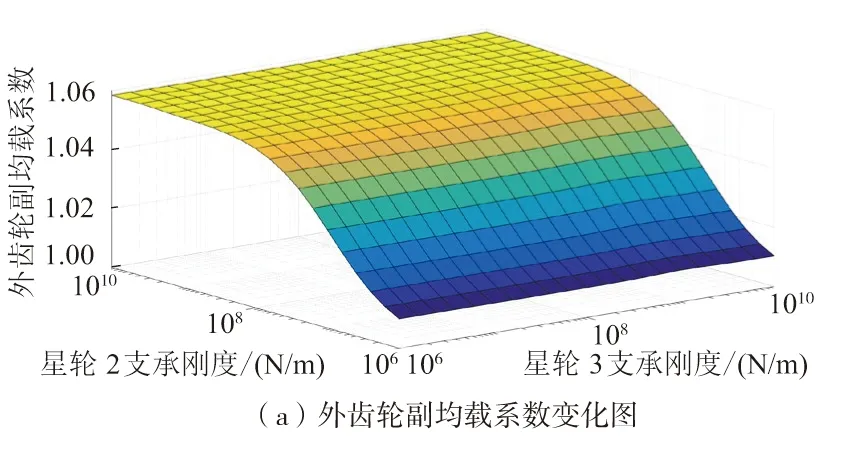
图5 系统均载系数随星轮支承刚度变化图

由图5可知，随着星轮2支承刚度的增大，系统内外齿轮副均载系数均逐渐增大，但变化速度逐渐变缓，当星轮2支承刚度>108N/m后，系统内外齿轮副均载系数逐渐逼近未考虑星轮横向振动均载分析模型的计算结果；系统内外齿轮副均载系数对星轮3支承刚度的变化不敏感。

4 结语

本文针对两级星型齿轮传动系统，提出了双联齿轮弯扭耦合振动边界条件，建立了考虑双联星轮横向振动的弯扭耦合动力学模型，开展了星轮支承刚度对两级星型齿轮传动系统均载特性影响分析。研究结论如下：

1)考虑星轮横向振动的均载分析模型，消除了星轮支承刚度足够大的假设，与实际模型更接近。

2)减小星轮支承刚度，可以有效地改善系统均载性能，相比星轮3支承刚度，星轮2支承刚度对系统均载系数的影响更大。