差速齿轮传动系统的动态啮合力影响规律研究

胡东根，李政民卿，张健

(南京航空航天大学 机电学院，江苏 南京 210016)

0 引言

差速齿轮传动系统具有结构紧凑、差速传动的特点，因此被广泛应用于汽车、船舶等传动领域。在准静态传递误差的内部激励下，系统将产生复杂的振动特性，既增大了噪声，也缩短了寿命。为此，开展差动齿轮传动系统的动力学特性研究具有重要意义。

国内外学者对差动齿轮传动系统动力学问题进行了研究。薛亮等[1]利用ADAMS软件进行了差速齿轮传动系统动力学仿真优化分析。肖泽艳等[2-3]设计了对称式行星差速齿轮传动系统，并对齿轮进行了静态和动态接触分析。VELEX P和MAATER M等[4]研究了齿轮制造和安装误差对差速齿轮传动系统振动和噪声的影响。

目前,对差动齿轮传动系统的动力学研究主要集中在定轴状态,对差动状态下的动力学特性研究较少。本文以差速齿轮传动系统为研究对象，建立了系统扭转振动模型，分析了系统在准静态传递误差激励下从定轴状态到差动状态的动力学响应，为差速齿轮传动系统的研制提供了技术支持。

1 传动系统结构及动力学模型

本文针对差速齿轮传动系统设计了如图1所示的构型方案。其主要包括两个部分：固定齿轮箱和差速齿轮箱。原动机输入经过锥齿轮1、锥齿轮2换向减速后，输出至锥齿轮3，差动输入直接作用在差动轮系中固定行星架的箱体上，最终动力输出至中间锥齿轮4。

图1 传动系统构型方案示意图

建立动力学模型如图2所示[5-7]。在建立该模型时，采用集中质量法，将原动机、联轴器、负载、齿轮、行星架等作为集中质量来处理，不考虑轴的质量，将其处理为扭转弹簧，并在齿轮啮合传动的过程中考虑齿轮间的啮合刚度和啮合阻尼。

图2 差速齿轮传动系统动力学模型

2 系统的振动微分方程

对于图2中的传动系统扭转振动动力学模型，以输入转矩作用下各个构件产生的运动方向为各自角位移运动的正方向。不考虑连接轴自身的质量，将原动机、齿轮、联轴器以及负载分别简化处理成具有转动惯量的元件，并考虑齿轮4绕公转轴线方向的自由度。所以该动力学模型是具有10个自由度的扭转振动系统，其中9个自由度分别描述了系统中的9个转动惯量元件(原动机、齿轮1、齿轮2、中间联轴器、齿轮3、齿轮4、齿轮5、行星架、负载)的扭转振动位移θM、θ1、θ2、θC、θ3、θ4、θ5、θH、θL，1个自由度描述了齿轮4绕公转轴线方向的扭转振动位移θr。

假设e为系统齿轮副间的准静态传递误差，并用不同的下标表示。由几何分析可得系统齿轮副间沿啮合线方向的位移如下：

(1)

式中：xij表示齿轮i、j间齿轮副沿啮合线方向的位移；Ri表示齿轮i的基圆半径；eij表示齿轮i、j间齿轮副的准静态传递误差。

根据上述啮合线位移分析，易得各齿轮副间的动态啮合力为

(2)

式中：Wij表示齿轮i、j间齿轮副的动态啮合力；cij表示齿轮i、j间齿轮副的啮合阻尼；kij表示齿轮i、j间齿轮副的啮合刚度。

由此可推得系统动力学方程如下：

(3)

当差动输入为0时，此时控制行星架运动的箱体固定不动，动力学方程变为

(4)

式中：IM、I1、I2、IC、I3、I4、I5、IH、Ir、IL分别为10个集中转动惯量；c1、c2、c3、c4分别为各传动轴的扭转阻尼；c5表示轴承的支撑阻尼；k1、k2、k3、k4分别为各传动轴的扭转刚度；k5表示轴承的支撑刚度;c12、c34、c45分别为各齿轮副的啮合阻尼；k12、k34、k45分别为各齿轮副的啮合刚度；TM和TL分别为作用在原动机与负载上的转矩；TH表示差动输入的力矩；r表示中间锥齿轮4到公转轴线的半径；W12、W34、W45分别为各轮齿啮合的动态啮合力。

3 传动系统的准静态传递误差分析

在齿轮啮合传动的过程中，准静态传递误差(static transmission error,STE)是齿轮传动系统中动力学关键激励，在做传动系统动力学特性分析前，求得系统准静态传递误差是必不可少的。准静态传递误差定义为：“从动轮实际位置与理想位置之间的差值”，理想位置指的是主、从动轮均为理想渐开线齿廓且无弹性变形时从动轮的位置。准静态传递误差可表示为

STE=δ2-δ1+Δf∑

(5)

式中：δ表示轮齿沿啮合线方向的变形量，下标1和2分别表示主动轮和从动轮；Δf∑表示系统等效误差，主要由齿形误差ff、中心距安装误差fa、基节误差fpb以及齿向误差fb组成。将上述4种误差沿啮合线方向拟合，有

(6)

针对本文研究的差速齿轮传动系统，计算其准静态传递误差，其中定轴状态下传动系统的准静态传递误差曲线如图3所示。为方便后传动系统动力学特性分析，对准静态传递误差曲线进行傅里叶拟合，得到傅里叶拟合的曲线如图4所示。

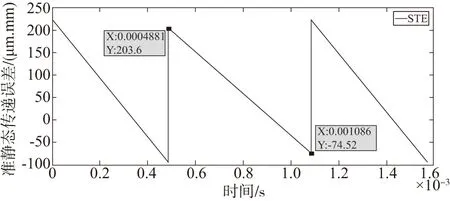
图3 稳态下准静态传递误差

图4 傅里叶拟合曲线

4 动态啮合力分析

在原动机正常工作时，主输入的功率为15 kW，转速为6 000 r/min。针对振动微分方程式(4)采用四阶龙格-库塔方法求解，然后将求解出的结果作为振动微分方程式(3)中各变量的初始状态，并采用四阶龙格-库塔方法求解，然后根据式(2)求解齿轮3、齿轮4间齿轮副从定轴状态到差动状态下的动态啮合力。动态啮合力幅值先快速衰减，后保持不变，动态啮合力随时间周期变化，如图5所示。

图5 动态啮合力变化图

改变差动输入转速，分别求解系统在不同差动输入转速下快速衰减阶段和周期变化阶段的最大动态啮合力。结果表明：当差动输入正向时，快速衰减阶段的最大动态啮合力随着转速增大而减小；反向时，随着转速增大而增大，如图6所示。当差动输入正向时，周期变化阶段的最大动态啮合力随转速增大而增大；反向时，随着转速增大而减小，如图7所示。

图6 快速衰减阶段最大动态啮合力变化趋势图

图7 周期变化阶段最大动态啮合力变化趋势图

5 结语

本文根据设计的传动系统结构，建立传动系统的动力学模型和系统振动微分方程，计算齿轮副的准静态传递误差，并将其作为传动系统的动态激励。通过Matlab/Simulink求解系统振动微分方程，改变差动输入转速的大小和方向，进行动态啮合力分析。结论如下：

1)差速齿轮传动系统从定轴状态到差动状态时，动态啮合力的幅值先快速衰减，之后保持不变，动态啮合力随时间周期变化。

2)传动系统从定轴状态到差动状态下，动态啮合力振幅在快速衰减阶段的最大值会随着差动输入转速大小和方向的变化而变化；正向时，最大动态啮合力随着转速增大而减小；反向时，随着转速增大而增大。

3)不同差动输入下，进入周期变化阶段的动态啮合力相较于定轴状态会发生变化，差动输入正向时，最大动态啮合力增大，反之减小，且正向时，随着转速增大，最大动态啮合力增大，反向时，随着转速增大而减小。