叶片式阻尼器的参数辨识研究

郭鑫星，周瑾，曹晓彦，郭勤涛

(南京航空航天大学 机电学院，江苏 南京 210016)

0 引言

直升机在飞行过程中，操纵系统的振动会给驾驶员的操作以及仪器设备带来严重的影响。为了解决这一问题，在操纵系统中加入减振装置是有效的解决方案之一。目前，操纵系统的减振方式主要采用被动减振形式，而叶片式阻尼器作为一种新型阻尼器，它具有行程大、布置灵活、散热性能好和防护性能高等优点而被广泛应用于各种减振系统中。

为了研究叶片式阻尼器的出力特性并建立准确的阻尼器模型，需要对阻尼器进行示功试验。由于其出力与旋转角位移、旋转角速度及振动频率均相关[1]，并呈现出较强的非线性关系，这给实际的动力学建模带来了一定的困难。为了解决这一问题，相关学者对阻尼器建模做了大量的研究。KWOK N M等[2]于2006年提出了双曲正切模型，通过双曲正切函数来描述阻尼器的迟滞特性；KRAUZE P等[3]用双曲正切模型建立了磁流变阻尼器的模型，并与Bouc-wen模型进行了比较；CHENG M等[4]利用考虑激励的双曲正切模型对阻尼器进行了仿真并优化。本文主要选用双曲正切模型以及双曲正切改进模型对阻尼器进行参数辨识,通过仿真和实验的对比，验证了这两种模型的有效性。

1 叶片式阻尼器

叶片式阻尼器主要由壳体、隔板、转子叶片、阻尼调节装置以及阻尼介质组成。它的主要工作原理为：当振动物体受到激励时，通过连接臂带动转子叶片旋转，形成高压腔和低压腔；油液由于压力作用，从高压腔流向低压腔，由于阻尼通道的节流作用，产生阻尼力。图1为叶片式阻尼器的实物图及内部结构图。

图1 叶片式阻尼器实物图及内部结构图

2 示功试验

为了得到叶片式阻尼器的出力特性，需要对其进行示功试验来得到位移特性图和速度特性图，然后通过实验数据来建立阻尼器的动力学模型。本次试验使用的试验机是MTS液压疲劳试验机，它在低频下具有良好的波形图，能够准确地给出指定的位移曲线。为了实验的可行性，需要在叶片式阻尼器上安装连接臂，通过连接臂将直线运动转化为阻尼器叶片的旋转运动[5]，如图2所示。试验机和阻尼器的安装示意图如图3所示。

图2 阻尼器力臂示意图

图3 试验装置系统

为了验证阻尼器在不同工况下的性能，示功试验使用正弦信号作为激励信号，幅值分别为1 mm、1.5 mm、2 mm，每个幅值下分别有1 Hz、2 Hz、3 Hz 3种频率，共有9种工况。完成示功试验后，为了能够更加直观清晰地表达叶片式阻尼器的出力特性，将上连接杆的位移通过式(1)转换为阻尼器叶片的旋转角位移(分别对应幅值为0.012 5 rad、0.018 6 rad、0.024 8 rad的简谐运动)，再通过对时间的微分得到角速度，将上连接杆受到的力根据式(2)转换为阻尼器产生的力矩。

(1)

T=F·sinα·LOA·sin(θ+α)

(2)

在示功试验后通过上述处理得到叶片式阻尼器力矩-角位移、力矩-角速度图，如图4所示。

图4 各工况下的阻尼器示功图

3 参数辨识

3.1 顺序选择遗传算法

遗传算法是由1962年由Holland提出的一种算法，它实质上是一种进化算法，在很多领域都有广泛的应用。通过遗传算法，一些多模型、多目标、非线性的函数优化问题能够方便地得到较好的结果[6-7]。遗传算法主要包括选择、交叉、变异三个主要过程，根据目标函数的值来确定是否继续进行寻优，从而得到最优解。目标函数一般取实验值与仿真值之间的平方差，其具体公式为

(3)

式中：OF为目标函数值；n为实验数据个数；Tsimu(i)为第i个点的仿真值；Texp(i)为第i个点的实验值；Tmax为实验值中的最大值；Tmin为实验值中的最小值。

顺序选择遗传算法是一种改进型的遗传算法，它与基本遗传算法的主要区别是两者个体选择操作的不同。基本遗传算法中个体的选择概率与个体的适应度值直接相关[7-8]，其计算公式为

(4)

式中：fitness(xi)为个体的适应度值；NP为种群个体数；Pi为个体的选择概率。

式(4)中如果某个个体适应度值为0，那么它的选择概率为0，这个个体就不能产生后代，这是基本遗传算法一个很大的缺点。而顺序选择遗传算法则将选择概率固定为某一个确定的值，其具体步骤为：

1)按适应度值大小对个体进行排序；

2)定义最好的个体的选择概率为p,则排序后第j个个体的选择概率为

(5)

从式(5)可以看出，每个个体被选择的概率均不为0，从而保证了遗传算法的精确性。

3.2 双曲正切模型

由于叶片式阻尼器的强非线性，普通模型难以准确预测其出力，需要寻找一种滞回模型来模拟阻尼器的滞回特性。常用的滞回模型主要有Bouc-wen模型和双曲正切模型(图5)。

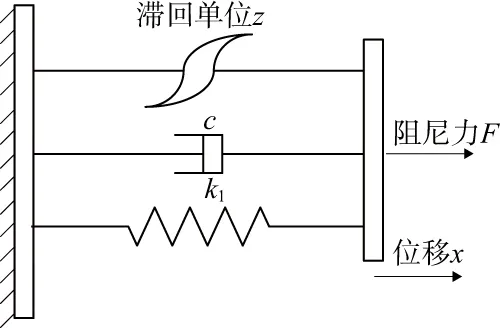
图5 双曲正切模型

双曲正切模型是一种利用双曲正切函数来描述阻尼器迟滞特性的模型，具有模型简单、易于识别、精度高等优点，适用于阻尼器的建模。它的公式为

(6)

式中：F为阻尼器的输出力；c为阻尼器的阻尼系数；k1为阻尼器的弹性刚度；k2、α、β为滞回环的形状参数；x为阻尼器的位移；f0为阻尼器的偏置力。

由于本文使用力矩-角位移、力矩-角速度特性图来描述阻尼器的特性，需将式(6)改写[9-10]，分别用角位移、角速度、力矩替代式(6)中的位移、速度、力，改写后的公式为

(7)

式中：T为阻尼器的输出力矩；θ为阻尼器的角位移；T0为阻尼器的偏置力矩。

3.3 双曲正切改进模型

为了使上述的双曲正切模型更加精准地模拟阻尼器的非线性特性，可以通过在和角速度相关的项加上一个指数系数来进一步修正阻尼器的仿真出力曲线。改进后的模型公式为

(8)

式中n为角速度指数系数。

本文主要采用双曲正切模型和双曲正切改进模型来对阻尼器进行参数辨识，其参数辨识结果如表1、表2所示。从辨识的结果中可以看出两种模型的c值均随着频率的增大而减小，随着幅值的增大也有减小的趋势，这是由于阻尼器内部油液的剪切稀化效应所导致的。k1值随着频率的增大而增加，随着幅值的增大变化较小，这与阻尼介质的可压缩性有关。参数中k2、α、β则在一个范围内浮动，没有明显的规律性。T0则是一个较小的值，这是因为实验室阻尼器是新型双通道式叶片阻尼器，改善了单通道叶片阻尼器偏置力较大的现象。

表1 双曲正切模型的参数辨识结果

表2 双曲正切改进模型的参数辨识结果

4 模型验证

4.1 双曲正切模型验证

通过参数辨识得到双曲正切模型的参数后，将其代入模型并在Matlab中仿真，得到仿真实验对比图如图6所示。从图中可以看出双曲正切模型能较好地模拟实验室叶片式阻尼器的出力特性，但在部分区域还存在一定的误差。

图6 各工况下实验仿真对比图

4.2 双曲正切改进模型验证

将辨识得到的参数代入双曲正切改进模型并在Matlab中进行仿真，得到的仿真示功曲线如图7所示。图中示功曲线从里到外分别代表1 Hz、1.5 Hz、2 Hz工况下的示功曲线，tanh1代表双曲正切模型，tanh2代表双曲正切改进模型。从图中可以看出，双曲正切改进模型在双曲正切模型的基础上进一步提高了模型的精度，尤其是在力矩与角速度的特性上，使得模型更加符合真实的曲线。这是因为阻尼器中的黏性力与速度不一定完全成线性关系，加入指数后，可以使得两者关系更加符合实际情况。从表2中目标函数值来看，双曲正切改进模型的值小于双曲正切模型的值，这也表明了双曲正切改进模型具有更好的精度(本刊为黑白印刷，如有疑问请咨询作者)。

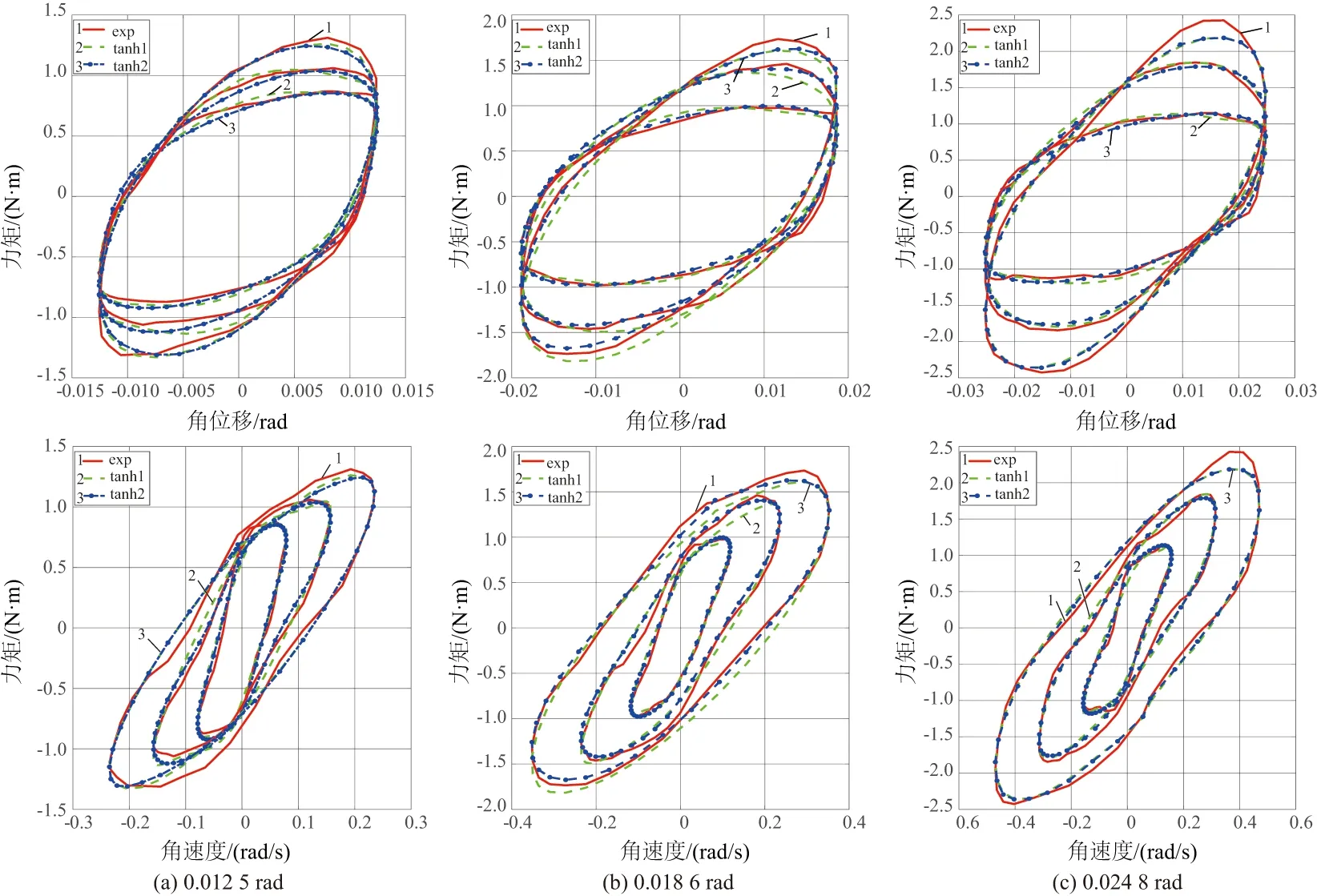
图7 改进后各工况下实验仿真对比图

5 结语

本文针对实验室的一种叶片式阻尼器进行了出力特性的研究。首先通过示功实验采集了阻尼器9种工况下的实验数据，然后以双曲正切模型为基础，将其转化为力矩形式，对修改后的模型进行了指数修正，用顺序选择遗传算法分别对双曲正切模型和双曲正切改进模型进行了参数辨识。结果表明，辨识得到的模型误差较小，可以很好地模拟实验室阻尼器的出力，而双曲正切改进模型则进一步提高了模型的精度，对以后叶片式阻尼器的建模具有一定的参考价值。