连梁阻尼器的初步设计方法

陈 彬

(成都市建筑设计研究院,四川成都 610015)

1 概述

消能减震技术是通过在结构中某些相对变形较大的部位安装阻尼器，通过阻尼器消耗地震输入能量，来实现消能减震效果。

对于弯曲变形为主的剪力墙结构，墙肢为主要承重构件，不能破坏；连梁作为地震下的第一道防线首先屈服，因此阻尼器可以布置在连梁处[1]，本文称为“连梁阻尼器”，连梁阻尼器通常有两种布置方式：一是将原有的连梁在中部断开，布置阻尼器,见图1；二是不改变原有的连梁，另外附加一道连梁，在其中部布置阻尼器，见图2。为了便于区分，本文将前者称为“单连梁阻尼器”，后者称为“双连梁阻尼器”。

图1 单连梁阻尼器

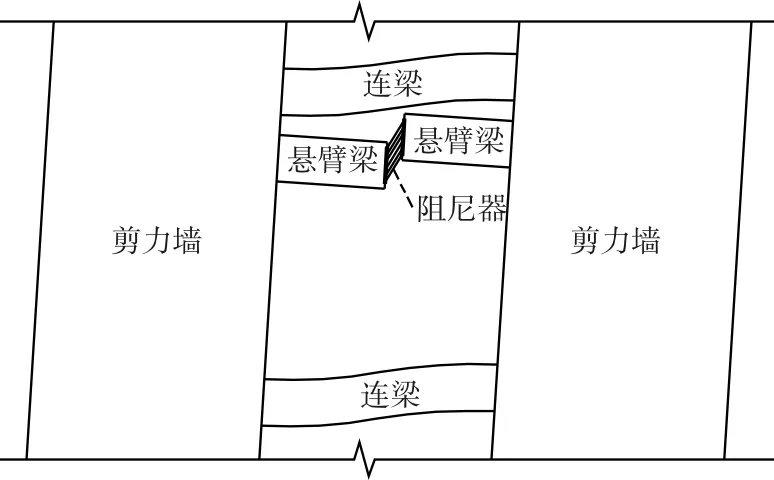
图2 双连梁阻尼器

与横放型阻尼器相比，连梁阻尼器由于是布置在连梁中，额外占用空间较小，更有利于满足建筑空间及使用功能要求。

2 阻尼器变形分析

在消能减震方案前期比选阶段，对于尚未布置阻尼器的结构，需要建立一个能够方便预测阻尼器布置后，阻尼器所能产生的变形的简便方法。本文以单连梁阻尼器为例，从阻尼器所在跨两端上下楼层的4个结点的变形入手，推导出连梁阻尼器的变形。4个结点如图3的点1、2、3、4，当结构变形后，4个结点的水平和竖向位移分别为(ui，vi)，i为结点编号，i=1,2,3,4。

对于连梁阻尼器，根据图3所示，阻尼器的变形可采用下式进行表达：

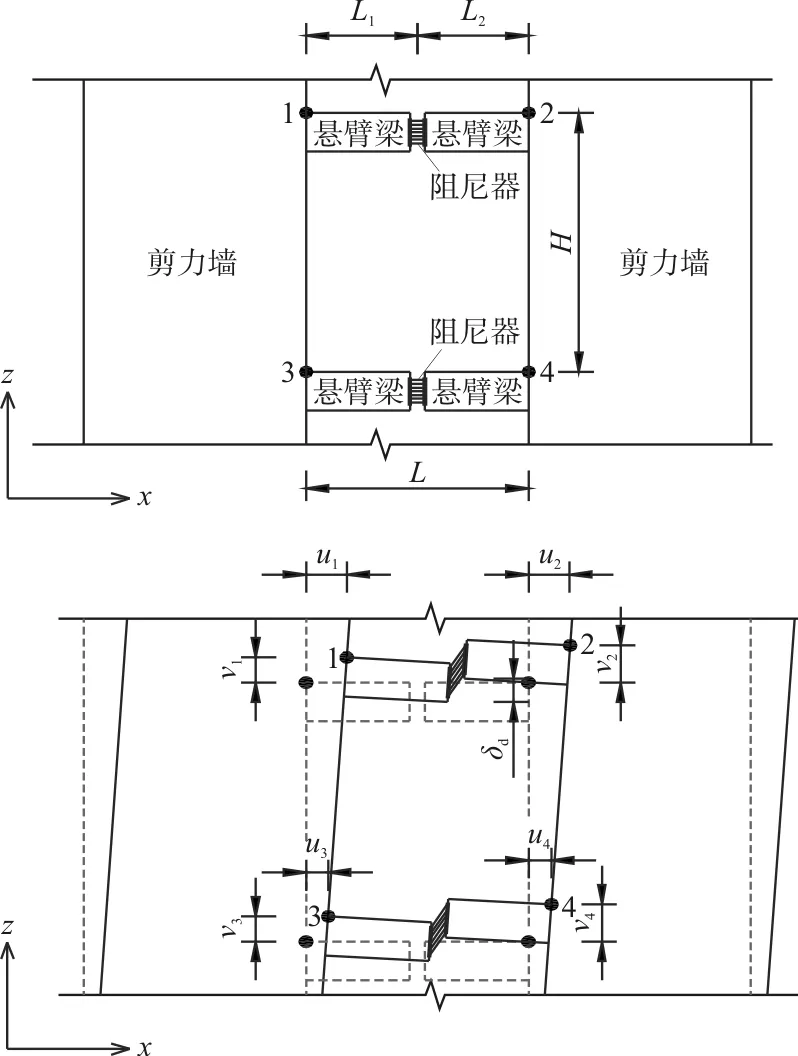
图3 单连梁阻尼器

(1)

式中：H为层高，H1、H2分别为阻尼器中心到上、下楼层的距离，且H=H1+H2；L为连梁跨度，L1、L2分别为阻尼器中心到左、右墙肢边缘的距离，且L=L1+L2。

对于单连梁阻尼器，H1=0，H2=H，阻尼器变形可简化为：

(2)

若各楼层采用刚性隔板假定，可令u1=u2=u12，u3=u4=u34，式(1)可进一步简化为：

(3)

可以看出：式(3)第一项表示阻尼器所在跨的上、下楼层的水平位移之差引起的阻尼器变形，第二项表示阻尼器所在跨的上、下楼层的转角之和引起的阻尼器变形，即：阻尼器变形是由阻尼器所在跨的上、下楼层的水平位移之差与转角之和共同引起的。一般情况下，在正X向地震作用下，第一项是正的，第二项取决于阻尼器所在跨的上、下楼层的转角，当该转角为“逆时针”时，此项为正，反之为负。

但应注意：以上计算方法是通过阻尼器所在跨度两端上下楼层的4个结点的位移来推算阻尼器变形。由此计算出的变形只是阻尼器“潜在”的最大变形，其中隐含着两个假定：一是假定结构在阻尼器位置处的变形完全由阻尼器吸收，即不考虑和阻尼器连接的构件的变形；二是假定阻尼器的刚度为零。因此，布置了阻尼器及其连接构件之后，阻尼器的实际变形将小于上述公式计算的结果。尽管如此，在前期方案比选阶段，仍可采用上述方法来评估阻尼器变形。

3 连梁阻尼器力学参数初步设计方法

当某一结构需要布置阻尼器时，需要在不影响原结构受力性能(如：自振周期、刚度)的前提下，估算出阻尼器的力学参数(如：刚度、屈服荷载、屈服位移、极限位移等)。当采用连梁阻尼器时，需要将原有的连梁在中部断开并布置阻尼器，原连梁转变为悬臂梁，从而对原结构的受力性能产生影响，为此，本文提出在不影响原结构受力性能的前提下的连梁阻尼器刚度的两种设计方法。

由于将原结构连梁断开并布置阻尼器，原连梁被两段悬臂梁与阻尼器所代替，因此，如果对阻尼器和悬臂梁刚度进行设计后，使两悬臂梁与阻尼器组成的系统在刚度上和原连梁接近，则可认为布置连梁阻尼器不影响原结构受力性能。设计方式有两种：一是不改变连梁截面，即悬臂梁截面和连梁一致，仅设计阻尼器；二是改变连梁截面，即悬臂梁截面不再和连梁一致，同时设计阻尼器和悬臂梁。

3.1 连梁阻尼器刚度等效方法一

从连梁的变形模式(图4)和结构力学原理[2]可得，连梁的横向刚度为：

(4)

式中：E为材料弹性模量，I0为连梁截面惯性矩，其余符号含义见图4。当不改变连梁截面布置阻尼器后，假设阻尼器刚度为Kd，从悬臂梁的变形模式(图4(b))和结构力学原理可得，悬臂梁的横向刚度为：

(5)

两悬臂梁和阻尼器组成的串联系统的横向刚度[2]为：

(6)

为了使结构的受力性能不发生改变，两悬臂梁和阻尼器组成的串联系统的横向刚度应与连梁的横向刚度相等，即：

K=K0

(7)

可得：

(8)

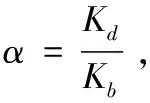
(9)

相应的阻尼器变形与串联系统总变形的比值为：

(10)

可以看出：阻尼器与悬臂梁的刚度比仅与连梁跨度L和阻尼器厚度Ld有关，与其它参数无关。如果在不改变连梁截面和原结构受力性能的前提下，设计出的阻尼器是无法选择其与悬臂梁的刚度比的。如果需要选择阻尼器与悬臂梁的刚度比，则要求悬臂梁截面不再和连梁一致，也就是连梁阻尼器刚度的第二种设计方法。

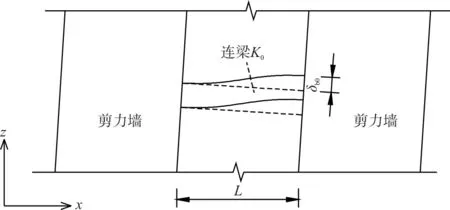
(a)连梁变形

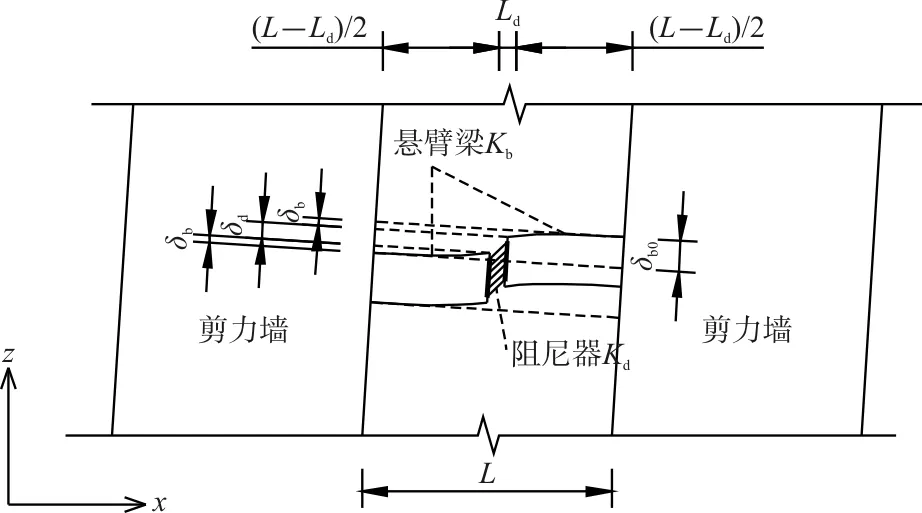
(b)阻尼器与悬臂梁变形图4 连梁、悬臂梁、阻尼器的变形

3.2 连梁阻尼器刚度等效方法二

为了使阻尼器和悬臂梁的具有所需要的刚度比α，可取阻尼器刚度：

Kd=αKb

(11)

两悬臂梁和阻尼器组成的串联系统的横向刚度为：

(12)

为了使结构的受力性能不发生改变，两悬臂梁和阻尼器组成的串联系统的横向刚度应与连梁的横向刚度相等，即：

K=K0

(13)

可得：

(14)

(15)

同时，悬臂梁的横向刚度为：

(16)

代入式(14)可得悬臂梁截面惯性矩I为：

(17)

若连梁和悬臂梁均为矩形截面，且两者截面宽度相等，则悬臂梁截面高度h为：

(18)

也就是说，如果在不改变原结构受力性能的前提下，通过选择适当的悬臂梁截面，可以设计出符合所需要的刚度比的阻尼器刚度。

3.3 连梁阻尼器刚度验证

为了验证第3.1、3.2节提出的2种连梁阻尼器刚度设计方法的准确性，本文采用ETABS建立一个30层单榀高层剪力墙结构模型，模型概况如表1所示。

表1 ETABS模型参数

各层连梁中布置阻尼器，阻尼器厚度取200 mm，分别采用以上2种方法计算阻尼器刚度：采用方法1时，阻尼器刚度由式(8)计算得385.103 kN/mm，悬臂梁截面和连梁一致；采用方法2时，分别指定阻尼器与悬臂梁刚度比为0.2，阻尼器刚度由式(5)计算得100.800 kN/mm，悬臂梁截面为300 mm×850 mm。分别计算该模型在布置阻尼器前、后的前3阶自振周期，计算结果如表2所示，可见：在连梁中布置阻尼器后，结构自振周期的变化非常小，最大变化率约为1.3 %。因此，本文提出的设计连梁阻尼器刚度的方法是合理的。

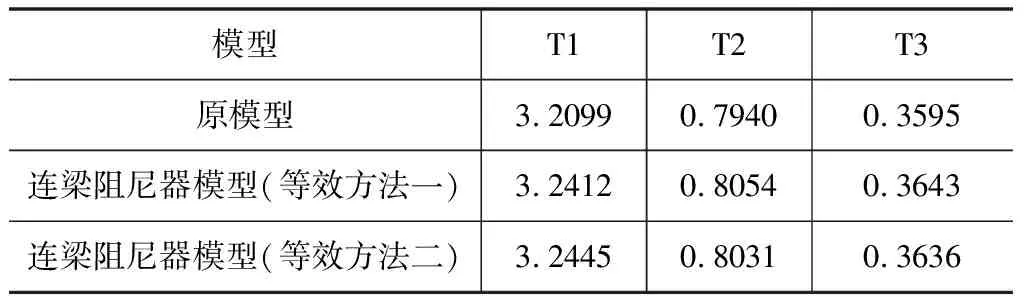
表2 布置阻尼器前、后结构自振周期对比 s

3.4 连梁阻尼器极限荷载、屈服荷载及屈服位移

根据阻尼器的设计原则，与阻尼器连接的主体结构构件(即悬臂梁)应考虑最大阻尼力作用，以保证阻尼器在罕遇地震作用下不丧失功能。《建筑消能减震技术规程》[3]7.1.6条规定：“与位移相关型或速度相关型消能器相连接的预埋件、支撑和支墩、剪力墙及节点板的作用力取值应为消能器在设计位移或设计速度下对应阻尼力的1.2倍”。由于阻尼器和悬臂梁是串联系统，所承担的剪力相等，依据该条规定，可认为阻尼器的极限荷载Fdu的1.2倍不应大于悬臂梁的屈服力Fby，该屈服力Fby同时取决于悬臂梁端部的受弯承载力Mby和受剪承载力Vby，即：

(19)

根据《混凝土结构设计规范》[4]11.7.7条，悬臂梁正截面受弯承载力为：

(20)

根据《混规》11.7.9条，悬臂梁斜截面受剪承载力为：

(1)跨高比大于2.5时：

(21)

(2)跨高比小于等于2.5时：

(22)

各符号含义同规范，从而可得阻尼器极限荷载Fdu。对于软钢阻尼器，极限荷载Fdu约为屈服荷载Fdy的2.5倍，从而可得阻尼器屈服荷载Fdy，即：

(23)

结合之前得到的阻尼器刚度Kd，可得阻尼器的屈服位移：

(24)

至此，连梁阻尼器的刚度、极限荷载、屈服荷载、屈服位移均可设计出来。当然，以上阻尼器参数还需要满足工程应用要求。

4 结论

(1)连梁阻尼器布置在连梁处，额外占用空间较小，更有利于满足建筑功能要求，是实现剪力墙结构消能减震、提高剪力墙结构抗震能力常用手段。

(2)在消能减震方案前期比选阶段，可采用本文提供的阻尼器变形分析方法来评估连梁阻尼器的变形。

(3)在消能减震初步设计阶段，在不改变原结构受力性能的前提下，可采用两种刚度等效方法设计连梁阻尼器的刚度，之后再设计出阻尼器的屈服荷载、屈服位移以及极限荷载等力学参数，可作为后续减震分析的参考依据。