具有柔性内齿圈的行星齿轮系统动态特性分析
2018-01-19王立新吴双马刘军辉陈林凯
王立新,吴双马,刘军辉,陈林凯
(郑州大学 机械工程学院,河南 郑州 450001)
1 引言
由于行星齿轮传动系统具有体积小、重量轻、可以实现分路传动、较大的传动比、效率高等优点[1],所以行星齿轮传动得到了广泛的应用。在实践中,振动和噪声一直是行星齿轮系统比较突出的问题,由于动态特性分析是分析振动和噪声的基础,所以行星齿轮系统的动态特性分析是大家关注的焦点。
研究行星齿轮的多数文献[2-3]都将行星齿轮系统的构件视为刚体,但是随着行星齿轮系统的高速化和轻量化,系统构件的变形会不断增大,尤其是作为薄壁结构的内齿圈,如果继续将其视为刚性,模型误差会比较大。
行星齿轮系统柔性构件的处理方法分为两种:(1)刚体有限元法[4-5]是将柔性构件分解为有限个刚体微段,段与段之间用虚拟的弹簧进行连接,弹簧的等效刚度用有限元软件分析出来。模型求解相对简单,但是精度不足。(2)柔性法是将构件完全柔性化,用经典弹性力学的知识分析构件,用微单元来处理柔性构件。但是如果将行星齿轮系统构件全部柔性化,会使得行星齿轮系统的运动微分方程异常复杂,难以求解。因此,将刚性模型和柔性模型[6-7]结合起来,仅考虑变形较大的内齿圈为柔性,其他构件为刚性,这样处理可以使得运动微分方程相对来说比较简单,也比较符合实际情况。纯扭转模型考虑因素比较简单,只考虑周向转动,方程比较简单,求解比较节省时间,在刚性模型中,常用来预测系统的固有频率[2,8]。但是,目前未见到文献使用刚柔耦合纯扭转模型分析系统的固有特性,所以加以探索。
2 模型的建立
建立具有N个行星轮的直齿行星传动系统的刚柔耦合模型,如图1所示。假设为平面机构,内齿圈为柔体,其他构件为刚体,太阳轮、行星架和行星轮均有1个周向自由度。齿轮间的啮合简化为弹簧系统,啮合力作用在齿轮的啮合线上,行星轮均布,润滑良好,忽略摩擦力、阻尼、陀螺效应等因素的影响。
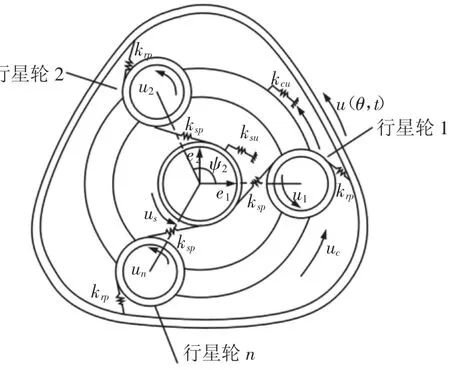
图1 行星齿轮系统的刚柔耦合模型Fig.1 The Rigid Flexibility Hybrid Model of the Planetary Gear System
取逆时针方向为正,下标c,r,s,p分别代表行星架、内齿圈、太阳轮和行星轮。内齿圈、太阳轮和每个行星轮之间的平均啮合刚度分别相等且为krp和ksp。kiu是构件的扭转刚度,Ii为系统各构件的转动惯量,其中,i=c,r,s,p。uj=rjθj(j=c,r,s,1,…,N)代表构件的扭转位移,θj—构件围绕自身轴心转动的角度;rj—基圆半径,但是rc—行星轮中心到行星架中心的距离。ψn—行星轮n相对于参考坐标系e1的角度,ψn=2π(n-1)/N(n=1,…,N)。对于内齿圈,u和w—其切向位移和径向位移;krus和krbs—切向和径向分布刚度;ρ—单位长度的质量;r—分度圆半径;v—泊松比;J—截面惯性矩;Ft—切向分布力;Fr—径向分布力。
2.1 内齿圈方程的建立
取内齿圈微段为分析对象,受力分析,如图2所示。运用牛顿第二定律对切向和径向进行分析,列写动力学方程:
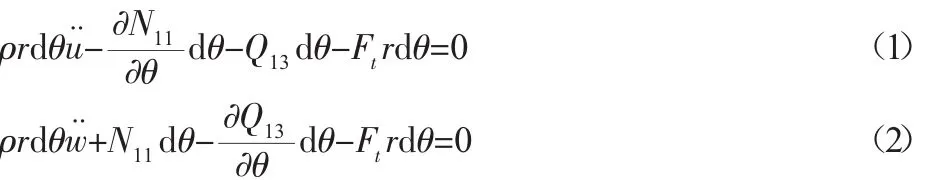
根据弹性力学知识可以得到:
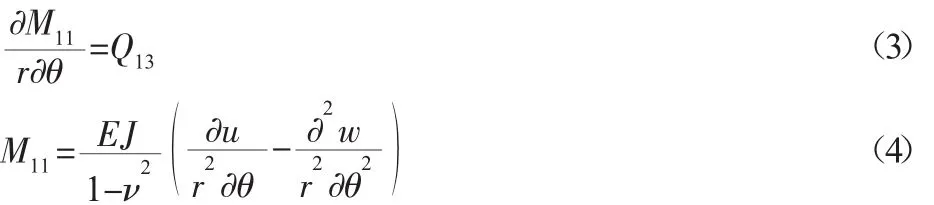
由内齿圈的不可延展性[9]可知:

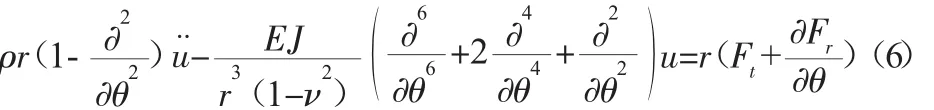
由式(1)~式(5),可以得出:Ft和Fr只能由啮合力和自身的弹性力提供。
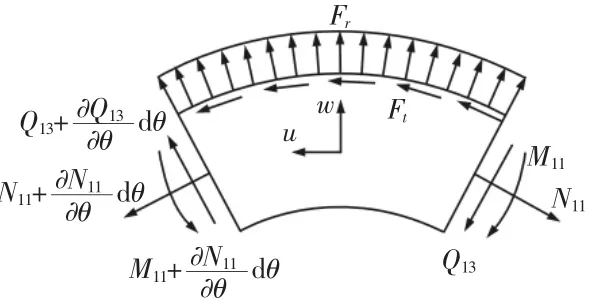
图2 内齿圈的微分段Fig.2 The Segment of the Ring
内齿圈与行星轮n相对位移分析,如图3所示。相对位移为:
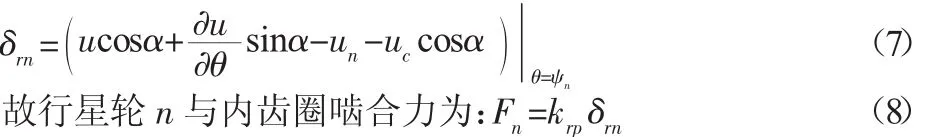

图3 柔性内齿圈与行星轮n的相对位移分析Fig.3 The Analysis of the Displacement of the Flexible Ring Gear and Planet
将行星轮n与内齿圈的啮合力分解为径向力和切向力,将径向力和切向力看成分布在啮合点附近的极小长度dl(dl=rdθ)内的分布力,因而引入δ函数,同时也避免了考虑复杂的边界条件,而Ftr和Frr相当于在(0,2π)上的分布力,所以:
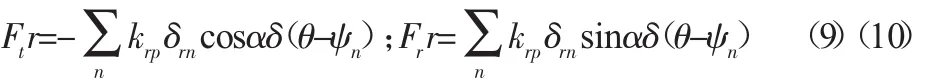
内齿圈自身的弹性为:
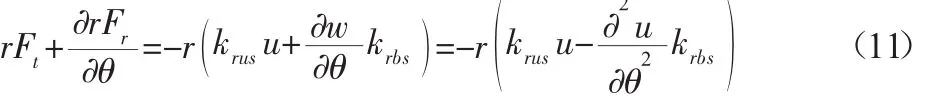
将等式(10)和等式(11)带入方程(6),整理可得方程(12)。为了把柔性变形和刚性位移分离开来,设:


式中:v—内齿圈面的振动变形;U0—内齿圈的刚体的转动;J—正整数,当J取的很大时,在等式(13)中误差就足够的小[6]。由于J没有限制,所以等式(13)可以应用到连续的柔性内齿圈中。把方程(13)带入方程(12)中,可得:
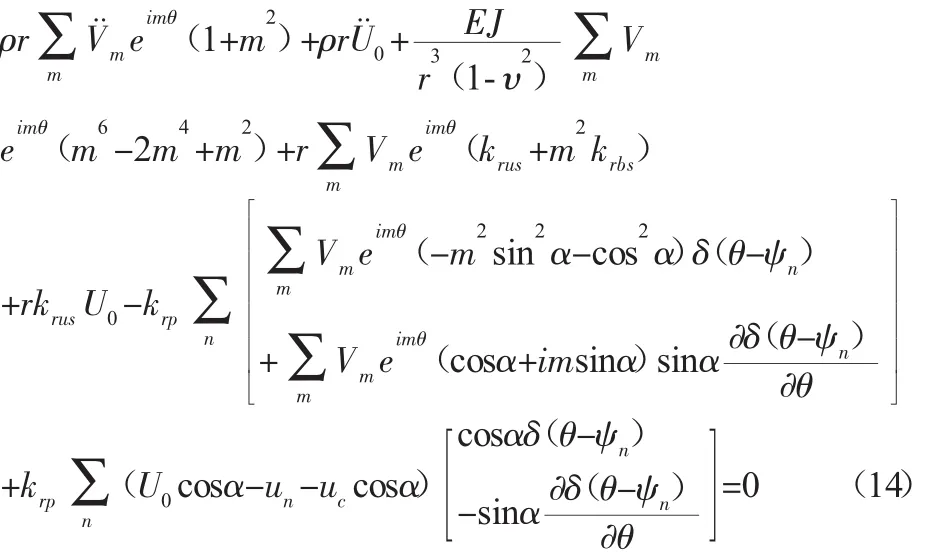
将方程(14)在(0,2π)上进行积分:
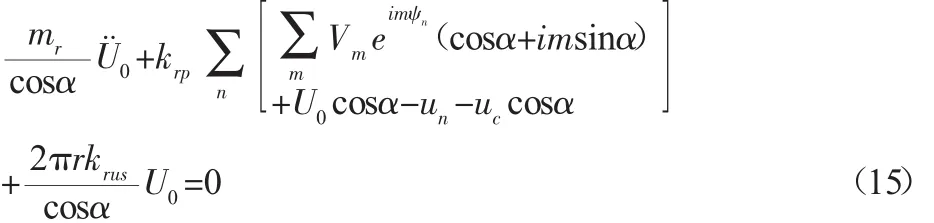
根据计算,可以得到:
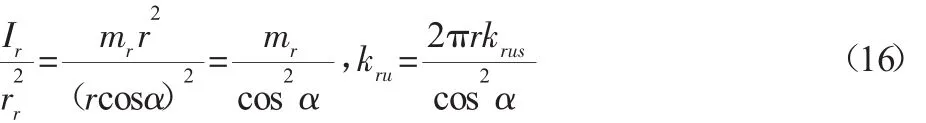
根据等式(16),并将方程(15)与刚性内齿圈方程[3]对比,可以得到:ur=U0cosα,Ir=mrr2(17)
所以内齿圈的刚性位移方程为:
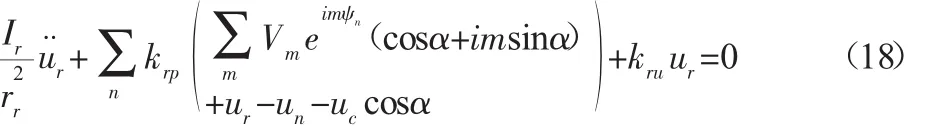
对方程乘以 e-ijθ,并对方程在(0,2π)进行积分,可以得到内齿圈的柔性变形方程。
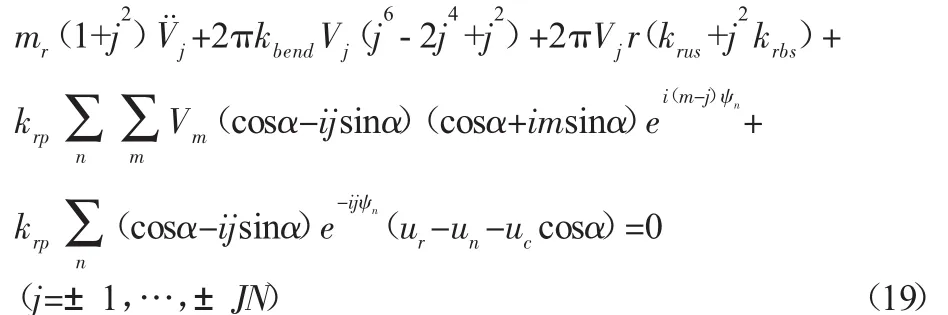
2.2 系统方程的无量纲化
为了计算方便和更精确,不再区分数值的单位,所以需要对方程进行无量纲化。
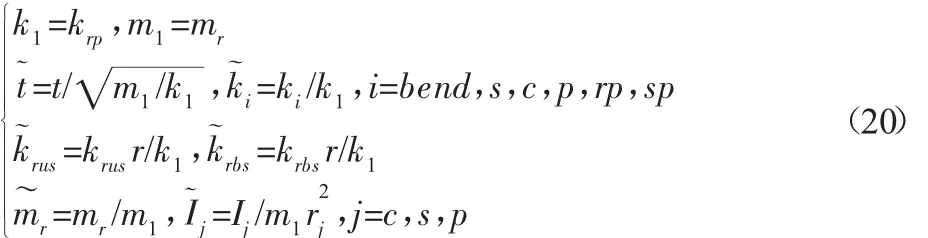
为了表示方便,下文中公式中省略了“~”。
2.3 系统的运动微分方程
由于行星齿轮系统中其他构件为刚性,所以将其他刚性构件的运动方程与内齿圈的柔性变形方程和扭转位移刚性方程相结合,得到了整个行星齿轮系统的运动方程。

在方程(22)~方程(25)中:
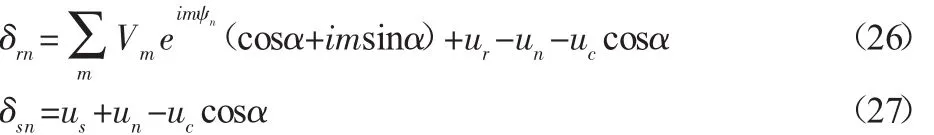
3 动态特性分析
3.1 方程的求解方法的确定
方程(21)到方程(25)经过整理,最终可以化为矩阵形式:

式中:M—质量矩阵;K—刚度矩阵;q—广义坐标矩阵。
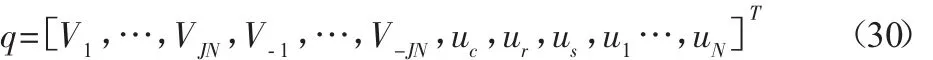
行星齿轮系统固有频率和振型的求解转化为特征值和特征向量的求解,由于方程过于复杂,采用MATLAB进行数值求解。
3.2 模态分析
行星齿轮系统的基本参数,如表1所示。当行星轮分别取为3、4、5,J=1时,刚柔耦合模型的各阶固有频率,如表2所示。为了便于比较,表2中还给出了刚性纯扭转模型的固有频率。

表1 直齿行星齿轮传动的基本参数Tab.1 Basic Parameters of the Spur Planetary Gear System
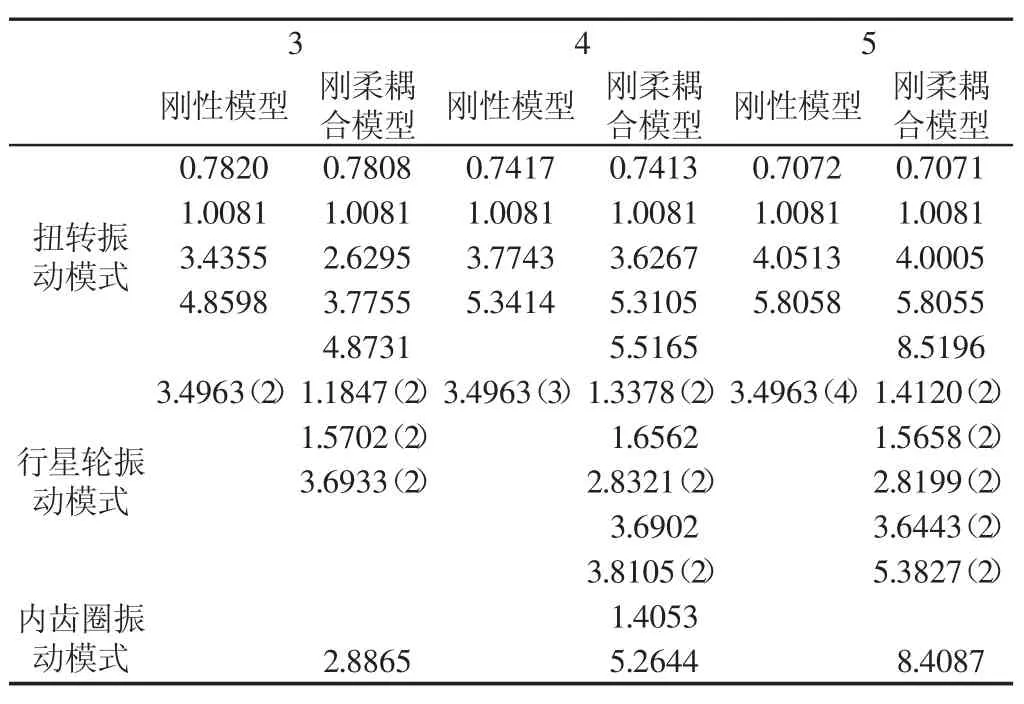
表2 行星齿轮系统的固有频率Tab.2 Natural Frequencies of the Planetary Gear System
根据振型的计算结果,当考虑内齿圈柔性时,系统的振动分为三种模式:扭转振动模式、行星轮振动模式和内齿圈振动模式,如图4所示。(1)在扭转振动模式中,系统中心构件的扭转位移均不为0,而且行星轮的扭转位移相等,即:u1=un(n=1,…,N)。(2)行星轮振动模式仅存在N≥2行星轮系中,在行星轮振动模式中,太阳轮、内齿圈和行星架的扭转位移均为0,而行星轮的扭转位移不为0;只有当N为偶数时,行星轮模式分为两种子模式,第一种子模式的行星轮位移关系为ui=-ui+1(i=1,…,N-1),其固有频率为单根,一共有(J+1)个,另一种模式的行星轮位移关系为 uj=-u(N/2)+j或uj=-u(N/2)+j(j=1,2,…,N/2)且ui≠ui+1(i=1,…,N-1),其固有频率为2重根,一共有(2N-4)J+N-2个。(3)在内齿圈振动模式中,各个刚性构件的扭转位移均为0,只有内齿圈的柔性变形。
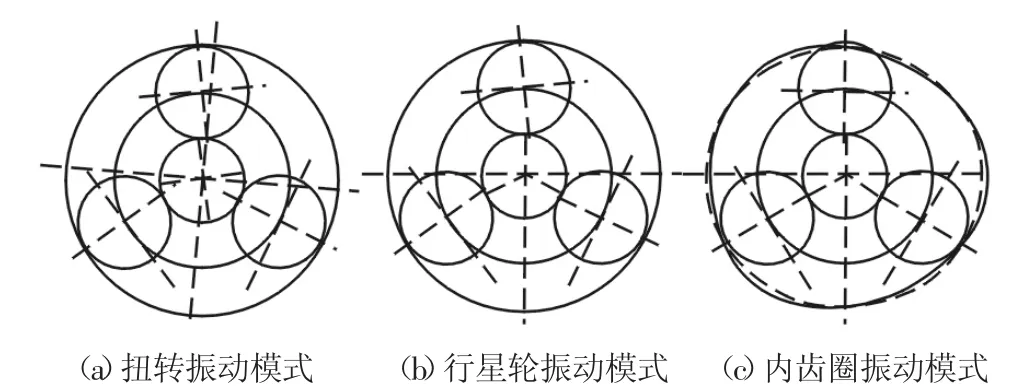
图4 行星齿轮系统的振动模式Fig.4 Vibration Modes of the Planetary Gear System
3.3 与集中参数模型的对比
由表2和表3可知,当考虑内齿圈柔性时,行星齿轮系统的动态特性发生了较大的变化。(1)当考虑内齿圈柔性时,行星齿轮系统产生了一种新的振动模式—内齿圈振动模式,使得固有频率的阶数增加了J(N为奇数)或2J(N为偶数)个。内齿圈振动模式仅体现了内齿圈的柔性变形,随着行星轮个数的增加,内齿圈振动模式的固有频率在增加。(2)柔性内齿圈对扭转振动模式有较大的影响,使得内齿圈固有频率的阶数增加J个,增加的固有频率一般为中高阶;而且随着行星轮个数的增加,第一阶固有频率出现下降,第二阶固有频率不变,其他阶固有出现明显上升。(3)柔性内齿圈对行星轮振动模式影响明显,当是偶数时,固有频率的个数增加了(2N-3)J个,当是奇数时,固有频率的阶数增加了(2N-2)J个,增加的固有频率一般为中低阶;随着行星轮个数的增加,低阶固有频率增大,高阶固有频率减小。(4)与刚性模型相比,当考虑内齿圈柔性时,固有频率的阶数增多,各阶固有频率下降。

表3 刚性模型与刚柔耦合模型的对比Tab.3 The Contrast the Rigid Model and the Rigid Flexibility Hybrid Model
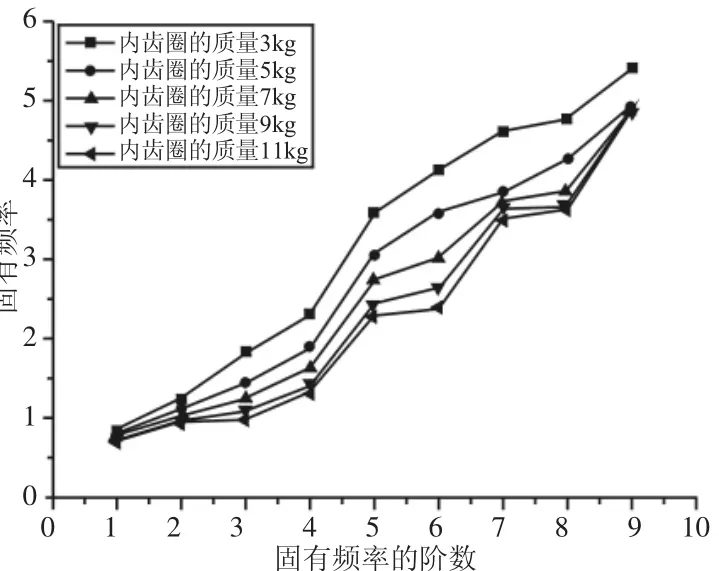
图5 内齿圈质量对固有频率的影响(N=3)Fig.5 The Effect of Ring’s Mass on the Natural Frequencies(N=3)
4 内齿圈柔性的影响
为了考察内齿圈的柔性对系统动态特性的影响,需要分析内齿圈柔性和固有频率之间的关系。内齿圈的柔性跟内齿圈的厚度息息相关,当其他条件一定时,内齿圈的厚度越薄,内齿圈的柔性越好,反过来,内齿圈越厚,内齿圈的柔性越差。与内齿圈的厚度直接相关的量就是质量,所以研究了内齿圈质量对行星齿轮系统固有频率的影响,如图5所示。随着内齿圈的质量减小,行星齿轮系统的各阶固有频率均出现上升,也就是说,内齿圈的柔性越大,系统的各阶固有频率越高;内齿圈柔性对固有频率影响的最大误差可达46.23%,因此在行星齿轮分析过程中内齿圈的柔性是至关重要的一个因素。
5 结论
通过建立具有柔性内齿圈的纯扭转模型,利用数值解分析了行星齿轮系统的动态特性,发现内齿圈柔性是影响行星齿轮系统动态特性的重要因素,并得出如下结论:(1)考虑内齿圈柔性时,行星齿轮系统的振动模式可以分为:扭转振动模式、行星轮振动模式和内齿圈振动模式;与刚性纯扭转模型相比,多出了一种内齿圈振动模式。(2)考虑内齿圈柔性时,行星齿轮系统的固有频率个数为2JN+N+3。当N为偶数时,行星轮振动模式的个数为(2N-3)J+N-1,当N为奇数时,行星轮振动模式的个数为(2N-2)J+N-1;扭转振动模式的个数为4+J;当N为偶数时,内齿圈振动模式的个数为2J,当N为奇数时,内齿圈振动模式式的个数为J。(3)与刚性纯扭转模型相比,考虑内齿圈柔性时,行星齿轮系统的对应固有频率均出现下降,而且内齿圈的柔性越大,行星齿轮系统的固有频率越高。因此,当设计行星齿轮系统时,为了避开外界干扰频率时,可以适当改变内齿圈的柔性。
[1]饶振刚.行星齿轮传动设计[M].北京:化学工业出版社,2003.(RaoZhen-gang.PlanetaryGearTransmissionDesign[M].Beijing:Chemical Industry Press,2003.)
[2]Kahraman A.Natural modes of planetary gear trains[J].Journal of Sound and Vibration,1994,173(1):125-130.
[3]王世宇,张策,宋轶民.行星齿轮传动固有特性分析[J].中国机械工程,2005(16):1461-1465.(Wang Shi-yu,Zhang Ce,Song Yi-min.Natural mode analysis of planetary gear trains[J].China Mechanical Engineering,2005(16):1461-1465.)
[4]郭明月.考虑内齿圈和太阳轮弹性的直齿行星轮系固有频率研究[D].郑州:郑州大学,2014.(GuoMing-yue.Researchonthenaturefrequencyofspurplanetarygeartrainwithelasticringandsun[D].Zhengzhou:ZhengzhouUniversity,2014.)
[5]张俊,宋轶民,王建军.计入齿圈柔性的直齿行星传动动力学建模[J].机械工程学报,2009,45(12):29-36.(Zhang Jun,Song Yi-min,Wang Jian-jun.Dynamic modeling for spur planetary gear transmission with flexible ring gear[J].Journal of Mechanical Engineering,2009,45(12):29-36.)
[6]Wu Xiong-hua,Parker R.G.Modal properties of planetary gears with an elastic continuum ring gear[J].Journal of Applied Mechanics,2008,75(3):1-12.
[7]陶庆,孙文磊,周建星.考虑齿圈柔性的行星传动系统固有特性与灵敏度研究[J].西安交通大学学报,2015,49(3):113-120.(Tao Qing,Sun Wen-lei,Zhou Jian-xing.Research on inherent characteristics and sensitivities of planetary gear transmission [J].Journal of Xi’an Jiaotong University,2015,49(3):113-120.)
[8]卜忠红,刘更,吴立言.行星齿轮传动动力学研究进展[J].振动与冲击,2010,29(9):161-166.(Bu Zhong-hong,Liu Geng,Wu Li-yan.Research advances in planetary gear trains dynamics[J].Journal of Vibration and Shock,2010,29(9):161-166.)
[9]Wu Xiong-hua,Parker R.G.Vibration of rings on a general elastic foundation[J].Journal of Sound and Vibration,2006,295(1-2):194-213.
