高转速泵地震工况下转子动力学分析

薛亚丽，石 红

（1.上海阿波罗机械股份有限公司，上海 201401；2.生态环境部核与辐射安全中心，北京 100082）

0 引言

某高转速泵是某型现役核电站的重要设备，属于核电三项安全专项设施之一。它的主要作用是在核电站正常给水系统失效时，向蒸汽发生器的相应回路提供足够的给水流量，以排出堆芯余热，直至停堆冷却系统RRA投入运行；在热停堆时和向冷停堆过渡期间，RRA投入运行前，代替给水系统，向蒸发器二次提供给水。转子作为该高转速泵的关键转动部件[1]，包含着关键水力部件，因此对其进行转子动力学的分析研究非常重要。

本文以用户对高转速泵在地震工况下参数的要求为基准，通过数值模拟的方式对高转速泵地震工况下转子动力学进行分析，并与用户要求的参数进行对比，验证泵组的转子动力学是否满足要求。

1 概述

由于该泵组属于高转速泵，其转子动力学特性对机组服役的高效性和安全性具有重要意义[2]。因此，为了保证泵组在临界转速等方面满足使用需求，需要对转子进行动力学分析。转子动力学计算包括转子临界转速计算和转子在激振力作用下的谐响应计算。

该高转速泵转子主要包括轴、首级叶轮、次级叶轮、诱导轮、平衡盘、汽机叶轮等。

（1）转子临界转速计算

根据用户要求，第一阶临界转速应大于工作转速至少25%，具体见式（1）：

式中 ncr1——转子的一阶临界转速；

n ——转子的额定转速。

扭振临界频率大于任何激励频率至少10%，具体见式（2）：

式中 ωcr扭转——扭转临界频率；

ω激励——转子的激励频率。

（2）转子在激振力作用下的谐响应

转子在激振力作用下的谐响应分析主要是计算在地震工况下，叶轮（与密封环配合处）的转子位移响应值是否小于其最小设计间隙值。

2 转子动力学分析

2.1 几何模型及有限元模型

基于UG建模软件建立的转子三维模型如图1所示。

图1 转子三维模型Fig.1 Rotor three-dimensional model

将几何模型导入到ANSYS，使用其网格划分工具生成实体单元，得到可供分析的有限元模型，如图2所示。

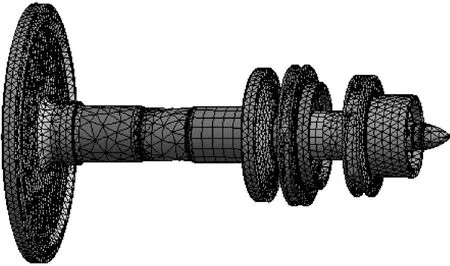
图2 转子有限元模型Fig.2 Rotor finite element model

2.2 轴承刚度

该高转速泵转子部件由水润滑轴承支撑，通过CFD模拟软件计算出水润滑轴承刚度K与轴承偏心率e之间的变化关系及轴承承载力随偏心率e的变化，计算结果分别如图3，4所示。

图3 轴承刚度K随偏心率e变化曲线Fig.3 Variation curve of bearing stiffness K with eccentricity e

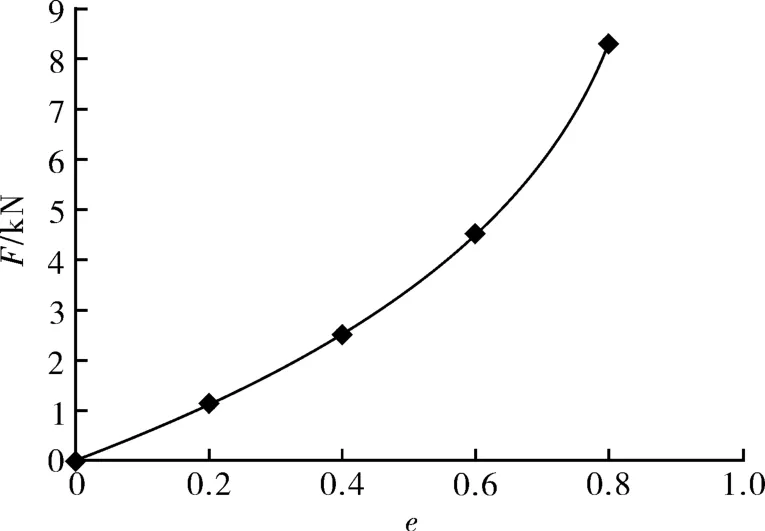
图4 轴承承载力F随偏心率e变化曲线Fig.4 Variation curve of bearing capacity F with eccentricity e

该泵组转子系统总质量为89.8 kg，重力取900 N，在轴承承载力随偏心率曲线中对应轴承偏心率约为0.2。

2.3 转子临界转速计算

转子临界转速计算需要考虑轴、叶轮、叶轮与密封环间隙、驱动机、轴承支撑刚度、阻尼和质量等因素[3]。

2.3.1 转子约束方式

泵转子部件的约束方式如图5所示，A处、B处为水润滑轴承，其轴承刚度见2.2节，约束Y、Z方向位移及Y、Z方向的转动自由度。

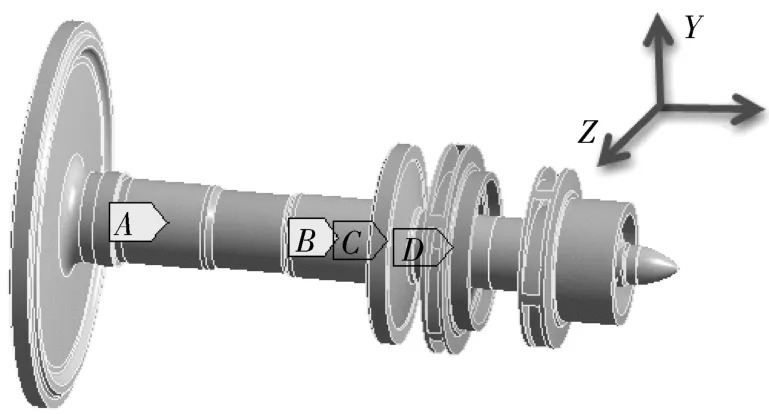
图5 转子约束方式Fig.5 Rotor restraint mode diagram

2.3.2 临界转速计算结果

按图5对模型进行约束，且把叶轮内含的介质以附加质量的形式加在叶轮上，计算获得各阶临界转速见表1，相应的坎贝尔图[4]如图6所示，各阶模态振型如图7所示。由表1可知，第一阶扭转临界转速为13 863 r/min，第一阶临界扭转频率为 231.05 Hz，激励频率为 133.33 Hz（n/60），满足第1节式（2）的要求；第一阶弯曲临界转速21 200 r/min，额定转速为8 000 r/min，满足第1节中式1的要求[5]；按照式（1）和式（2）计算后，对应的扭转频率和临界转速均满足要求。

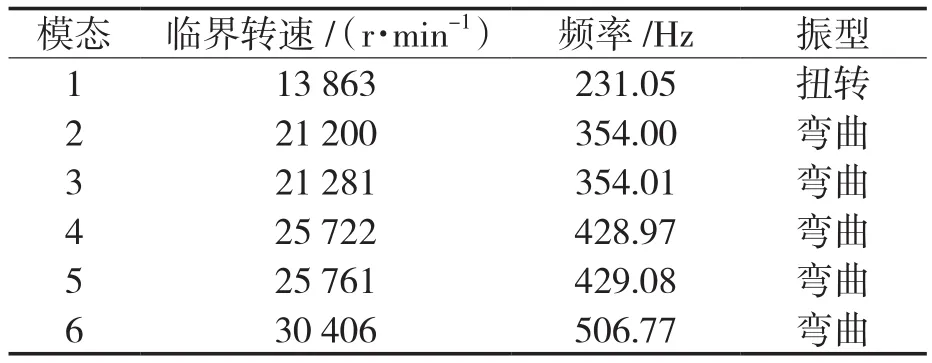
表1 临界转速计算结果Tab.1 Calculation results of critical speed

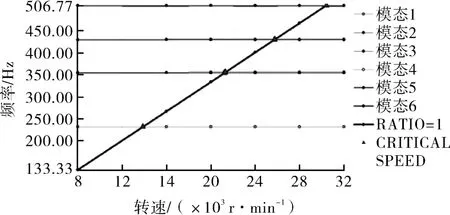
图6 坎贝尔图Fig.6 Campbell diagram

图7 各阶模态振型Fig.7 Modal vibration shape of each order

2.4 转子谐响应分析

分析用于确定线性结构在承受随时间按正弦（简谐）规律变化的载荷时的稳态响应称为谐响应分析，分析过程中只计算结构的稳态受迫振动，不考虑激振开始时的瞬态振动[6]，谐响应分析的目的在于计算出结构在相应频率下的响应值（通常是位移）对频率的曲线，从而能预测结构的持续性动力特性，验证设计是否能克服共振、疲劳以及其他受迫振动引起的有害效果。

为了分析该高转速泵叶轮水体对叶轮的径向力和泵轴不平衡量引起的不平衡径向力联合激振作用下的转子响应，采用ANSYS workbench 的Harmonic Response模块对该转子在地震工况下进行模态叠加法谐响应分析[7-10]。

2.4.1 残余不平衡质量

由于转子系统中诱导轮、首级叶轮、次级叶轮、平衡盘和汽机叶轮等转动部件质量分布不均匀，会产生残余不平衡质量，由此引起的离心力可用式（3）计算：

式中 Gc——转子的许用不平衡质量，g；

n ——转速，r/min；

R ——计算半径，mm。

通过式（3），带入转子各组成件的对应参数值，分别计算出正常工况下转子各组成件由残余不平衡量引起的离心力：Fe诱导轮=7.17 N；Fe首级叶轮=20.66 N；Fe次级叶轮=23.96 N；Fe平衡盘=22.83 N；Fe汽轮叶机=44.34 N。

将各组成件产生的不平衡力分别加载于转子系统中对应的位置，该泵组正常工况下转子激振力加载如图8所示。正常运行工况转子的工作转速8 000 r/min，对应的激振频率为133.33 Hz。

图8 正常运行工况转子激振力示意Fig.8 Schematic diagram of rotor exciting force under normal operating conditions

2.4.2 地震工况下转子谐响应分析

整个转子除了承受在正常运行工况下各部件的残余不平衡质量产生的离心力载荷外，再加载地震载荷形成地震工况，即水平方向（x和z）：±0.36 g，竖直方向（y）：±0.184 g。地震工况属于极端恶劣工况，高转速泵在地震工况下转子激振力加载如图9所示。地震工况时转子的工作转速仍为8 000 r/min，对应激振频率为133.33 Hz。

图9 地震工况下转子激振力加载示意Fig.9 Schematic diagram of rotor excitation force loading under earthquake condition

在激振频率下转子首级叶轮前密封环Y方向变形如图10所示。从图中可知其最大位移为0.007 283 8 mm。转子首级叶轮前密封环Y方向位移与激振频率的关系曲线如图11所示。

图10 首级叶轮前密封环Y方向变形Fig.10 Deformation diagram of front sealing ring of first stage impeller in Y-direction

图11 首级叶轮前密封环Y方向位移与激励频率曲线Fig.11 Y-direction displacement and excitation frequency curve of front sealing ring of first stage impeller

激振频率下转子首级叶轮后密封环Y方向变形如图12所示，从图可知，最大位移为0.004 293 3 mm。图13示出了转子首级叶轮后密封环Y方向位移与激振频率的关系曲线。

图12 首级叶轮后密封环Y方向变形Fig.12 Deformation diagram in Y-direction of rear sealing ring of first stage impeller

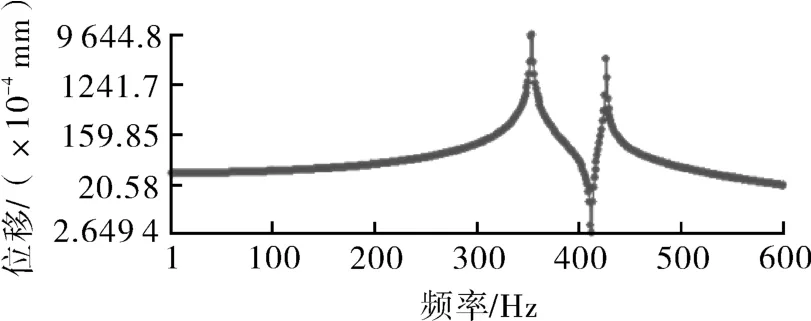
图13 首级叶轮后密封环Y方向位移与激励频率曲线Fig.13 Y-direction displacement and excitation frequency curve of rear sealing ring of first stage impeller

在激振频率下转子次级叶轮前密封环Y方向变形如图14所示，从图可知，其最大位移为0.002 776 7 mm。图15示出了转子次级叶轮前密封环Y方向位移与激振频率的关系曲线。

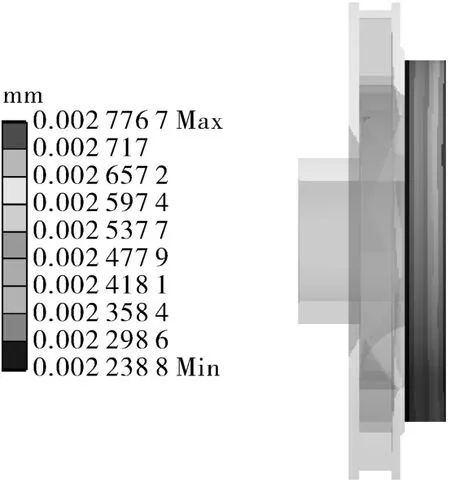
图14 次级叶轮前密封环Y方向变形Fig.14 Deformation diagram of front sealing ring of secondary impeller in Y-direction

图15 次级叶轮前密封环Y方向位移与激励频率曲线Fig.15 Y-direction displacement and excitation frequency curve of front sealing ring of secondary impeller

在激振频率下转子次级叶轮后密封环Y方向变形如图16所示，从图中可知其最大位移为0.001 699 2 mm。图17示出了转子次级叶轮后密封环Y方向位移与激振频率的关系曲线。

图16 次级后密封环Y方向变形Fig.16 Deformation diagram of secondary rear sealing ring in Y-direction

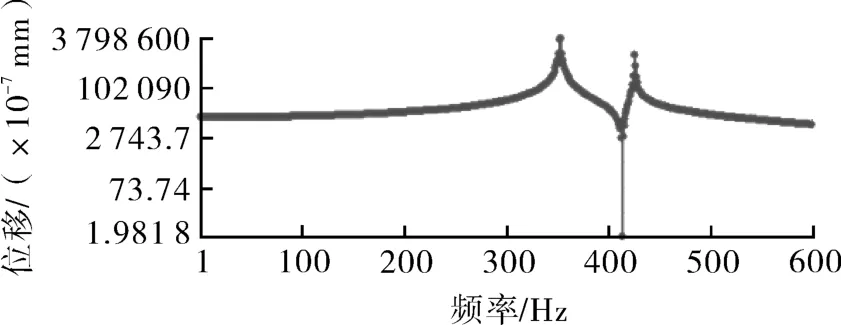
图17 次级叶轮后密封环Y方向位移与激励频率曲线Fig.17 Y-direction displacement and excitation frequency curve of rear sealing ring of secondary impeller

2.4.3 转子谐响应评定

地震工况下转子谐响应评定结果见表2，通过计算结果可知，地震工况下，转子不同位置的总位移量均小于设计间隙，转子谐响应评定结论安全。

表2 地震工况下转子谐响应计算值Tab.2 Calculated values of rotor harmonic response under earthquake condition

3 结论

（1）第一阶弯曲临界转速为21 200 r/min，满足大于额定转速的1.25倍（10 000 r/min）的要求；

（2）第一阶扭转临界转速为13 863 r/min，对应的第一阶临界扭转频率为231.01 Hz，而泵正常工作时的频率ω激励=133.33 Hz，显然满足ωcr激励＞1.1 ω激励；

（3）临界转速和扭转频率的计算结果表明该泵组在正常运行过程中转子不会发生共振，轴系安全可靠；

（4）转子在地震工况下，两级叶轮前、后密封环的设计动静间隙值均大于总位移量，表明泵组运行时不发生干涉，即地震工况下转子动力学满足设计要求。