二维隐蔽时间信道构建的研究*

刘 莉 徐芹宝 王昌达

（江苏大学计算机科学与通信工程学院 镇江 212013）

1 引言

最初在多级安全系统中，隐蔽信道（Covert Channel）是指可信系统中的高安全级用户，通过违反系统安全策略的方式将信息泄露给未授权用户的一种通信机制［1］。由于隐蔽通道所使用的通信媒介并不是为面上信道（Overt Channel）所设计的，因此隐蔽通道的容量远远小于其面上信道的容量。在包交换网络中，根据应用的通信介质，隐蔽信道大致可分为隐蔽存储信道（Covert Storage Channel，CSC）和 隐 蔽 时 间 信 道（Covert Timing Channel，CTC）。其中，CSC 使用数据包中约定的共享存储位置作为介质来传递隐蔽信息，如包头中的冗余位等；CTC使用与数据包传输相关的时间性介质作为通信介质，例如数据包发送频率、数据包间延迟等。一般地，可以通过流量归一化（Traffic Normalization）方法来消除CSC［2］，但CTC 至今无法被根除。目前有多种CTC的实现方法，如IPCTC［3］、JitterBug［4］、TRCTC［5］和MBCTC［6］等。目前对CTC的研究多集中在信道容量的扩容、信道的隐蔽性等方面。为了提高隐蔽信道的容量，本文提出了以伪包标识排列和数据包大小作为通信介质的二维隐蔽时间信道2dCTC，显著提高了现有CTC的通信容量。本文的主要贡献如下。

1）提出了一种以伪包标识排列和数据包的大小变化为通信介质的二维隐蔽时间信道2dCTC。实验结果表明，2dCTC比现有的一维CTC具有更高的信道容量。

2）设计了基于康托展开式2dCTC 编码与解码算法，提高了2dCTC的自动编码与解码效率。

2 相关工作

一般地，CTC 可分为以下3 类［8］：1）时隙信道：使用在一个时隙内传输的包的数量变化来对消息进行编码/解码；2）包间延迟信道：使用数据包传输的包间延迟（Inter Packet Delay，IPD）变化对消息进行编码/解码；3）排序信道：使用传输中数据包的ID顺序变化对消息进行编码/解码。

在第一类中，Cabuk 等［3］提出了第一个基于IP协议的简单时隙时间信道（Simple Time Covert channel，STC），该方法的主要思想是根据给定时隙内是否存在数据包来编码和解码二进制数1 或0。然而，这种方法需要发送方和接收方之间的时钟同步，而网络时钟精准同步相对困难。王昌达等［9］提出了利用在固定时间窗口内发送不同数量的IP 数据包传送多位比特，提高了传输容量，该方法同时给出了比特序列块的定界方法，因此无需时钟同步。

在第二类中，Berk等［10］提出了以相邻两个数据包传输之间的包间延迟为介质嵌入信息。在文献［7］中，通过模拟网络正常流量流的包间延迟构建CTC，由于此方法使得数据包传输的统计特性与正常数据包传输的统计特性几乎相同，所以构建的CTC具有更好的隐蔽性。Wu等［11］在CTC中引入了哈夫曼编码，在该方法中，发送者使用哈夫曼编码将隐藏消息编码到相邻数据包之间的时间间隔，该方法提高了信道的隐蔽性和容量。

在第三类中，El-Atawy等［12］提出了一种利用传输数据包ID 的排序作为隐蔽通信介质的技术。通过操控发送方模拟自然发生的数据包重新排序现象传递隐蔽信息，提高了CTC 的鲁棒性和隐蔽性性。Zhang等［13］设计了可变码长方案构造分组重组隐蔽定时信道。在该方法中，通过改变RTCP（Real Time Transport Control Protocol）数据包位置调整相邻两个RTCP 数据包内数据包的个数，来表示隐蔽消息，并且使用了格雷码提高信道的鲁棒性和不可检测性。

综上，已知的CTC 一般只使用一种通信介质，所以它们是一维CTC。为了大幅度提高CTC 的容量，本文首先提出了多维度CTC 的概念，然后作为应用的实例，构建了一个二维的时间信道2dCTC，最后理论分析与实验验证了2dCTC 具有高通信容量等优点。

3 二维隐蔽时间信道（2dCTC）的构建

本文提出的2dCTC，采用“数据包的伪包标识排列”和“数据包大小变化”相结合的二维通信介质对隐蔽信息进行编码。为便于理解，在讨论2dCTC方案之前，我们分别给出在上述两个维度上进行编码和解码过程。

3.1 基于伪包标识排列的编/解码方法

在包交换网络中，数据包在传输中的错序率大约在0.1%到3%之间［14］，这使得参与构建时间信道的数据包数量较少，其容量也相应较小。因此我们提出使用伪包标识，它是附加在数据包上取值唯一的数据块。与驻留在报头中的包ID 不同，伪包标识位于数据包的数据区域（payload area）中。图1给出了基于数据包伪包标识排序的信息编/解码的工作原理。

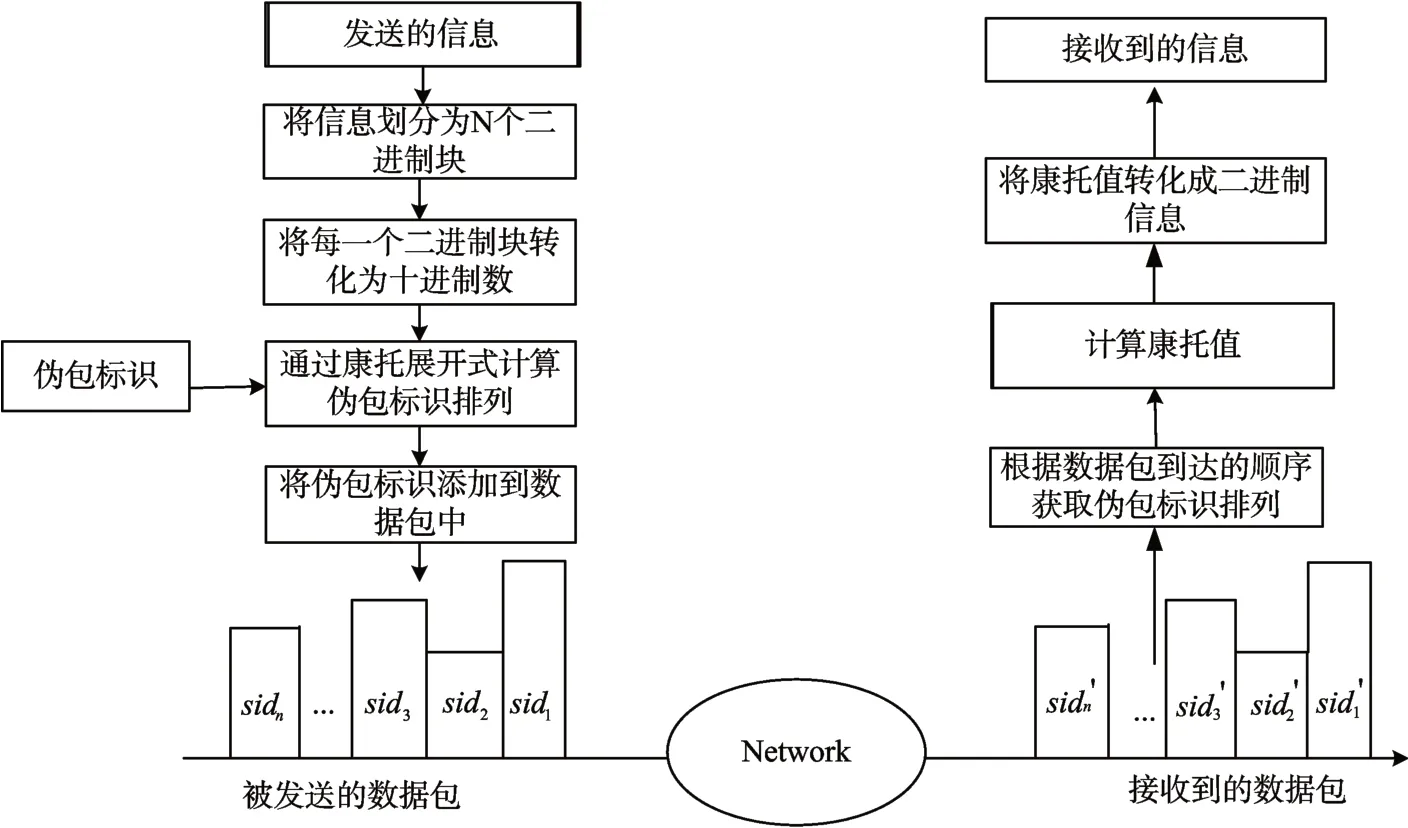
图1 基于数据包伪包标识排序的信息编/解码的工作原理

首先，将待传输的消息分为N个二进制块，即{s1，s2，s3…si…sN}，每个si包含L位二进制数。我们假设每一个si包含8位二进制数，每一个si对应十进制数为Si；{sidi|sidn∈R，i=1，2，3…n} 是数据包伪包标识的集合。则基于伪包标识排序的信息编/解码的主要步骤如下。

1）根据每个si包含的二进制的位数以及约束条件2L≤n!，计算编码表示每个si需要的数据包的个数n。因为，每个si包含8位，所以n=6。

2）根据Si的值，通过康托展开式［15］的逆运算得到相应的伪包标识排列{sid1，sid2…sidn} ，康托展开式的计算公式如下，见式（1）：

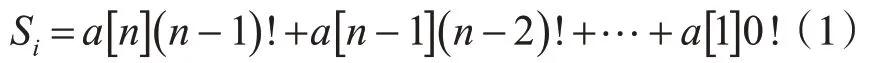
其中，Si表示康托值，a[i] 为整数，且0 ≤a[i] ≤i，0 ≤i≤n，表示当前元素在未出现元素中的序位。

使用康托展开运算代替映射表，分析其算法复杂性可知，当传输n个数据数时，运用康拓展开的逆运算的时间复杂度为O(n)，而运用映射表的复杂度为O(nlgn)。由此可见，运用康拓展开式以及康拓展开式的逆运算在计算速度上优势明显，确保了编码与解码的效率。

3）按照伪包标识排列中的顺序将伪包标识依次添加到数据包的有效负载区域，并发送数据包流。

4）在CTC的接收端，根据数据包的到达时间排列数据包的伪包标识，然后通过式（1）计算Si，从而解码出隐蔽信息。

为了更好地理解本节中的方法，在此提供一个示例。若si为00001011（对应的十进制数Si等于11）；伪包标识为{1 ，2，3，4，5，6} ，根据康托展开式的逆运算计算得到伪包标识排列：11÷5!=0…11，因此a[6 ] =0，sid1=1；11÷4!=0…11，所以a[5 ] =0，sid2=2；按照相同的方法计算可得，a[4 ] =1，sid3=4，a[3 ] =2，sid4=6，a[2 ] =1，sid5=5，sid6=3 。 因此，伪包标识的排列为{1 ，2，4，6，5，3} 。然后将{1，2，4，6，5，3} 依次添加到n个数据包的数据区域内，并以数据包流的方式发送。在接收端获取每一个数据包中的伪包标识，得到伪包标识的排列{1，2，4，6，5，3} ，然后通过康托展开式计算可得Si=11，si=00001011。

3.2 基于数据包大小变化的编/解码方法

使用数据包大小的变化对信息进行编码和解码，不易受数据包传输延迟、抖动等信道噪声的影响。图2 给出了基于数据包大小变化的消息编/解码方法的工作原理，主要步骤如下。

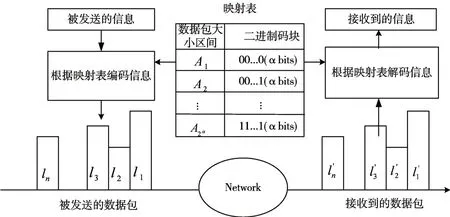
图2 基于数据包大小变化的消息编/解码方法的工作原理

1）通过公式M=HgB，R( )X统计数据包大小，其中，M为各组数据包个数；HgB，R是一个统计函数，计算每个分组中的数据包的个数；B为组距离，R表示要统计的数据包大小范围；X表示样本数据序列。

2）构建表示数据包大小与二进制块之间关系的映射表。如果一个数据包大小可以表示α位二进制数，则将通过（1）统计出的数据包个数较多的区域划分为2α个区间。

3）根据映射表及si，发送相应大小区间内的数据包。

4）接收端得到相应的数据包进行解码时，首先获取数据包的大小，根据数据包的大小通过查找映射表得到相应的信息。

为了更好地理解本节中的方法，此处提供一个示例。假设{li|li∈R，i=1，2…n} 表示数据包的大小，其中，li表示第i个数据包的大小，当数据包大小li≥l时，表示二进制中的“1”，否则表示“0”；si为00001011，数据包大小为l1＜l3＜l4＜l5＜l6＜l7＜l＜l8＜l2＜l9，则数据包发送的顺序为首先发送第1个数据包，然后依次是第3，4，5，8，6，2，9 个数据包。接收端得到需要的数据包，抓取数据包的大小依 次 为l1，l3，l4，l5，l8，l6，l2，l9，根据映射关系得到si=00001011。

3.3 二维隐蔽时间信道的构建

使用2dCTC方案对L位的信息进行编码，首先将消息为两个部分。第一部分（K位）信息通过数据包大小变化编码，另一部分（L-K位）通过数据包的伪包标识排列进行编码。图3 给出了2dCTC的工作原理。

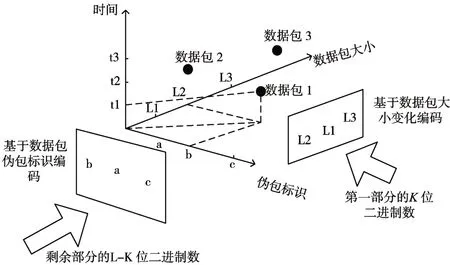
图3 2dCTC的工作原理

2dCTC编/解码的主要步骤如下：

1）根据式（2）计算编码过程中需要的数据包数量n：

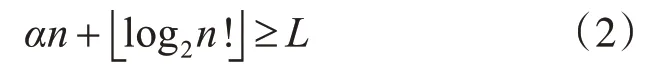
其中，α表示映射表中一个数据包大小所表示的比特数，k表示si从左往右的αn位。

2）通过数据包大小变化编码K位信息得到一组n个有序排列的数据包，并通过伪包标识排列编码L-K位信息。

3）将伪包标识按照排列中的顺序依次添加到有序的数据包中并以流的方式发送。

4）当接收端得到相应的数据包进行解码时，分别根据数据包大小变化的解码方法与基于伪包标识排列的解码方法解码信息。

算法1和算法2分别表示2dCTC的编码和解码过程。

为了更好地理解本节中的方法，此处提供一个示例。假设si=00001011；当数据包大小li≥l时，表示二进制中的“1”，否则表示“0”；数据包的大小变化满足：l1＜l3＜l4＜l5＜l＜l2；伪包标识序列为{1 ，2，3，4} ；根 据 式（2）可 知，n=4，K=0000，L-K=1011；第一部分K位信息根据基于数据包大小变化编码可知，数据包的发送顺序为第1 个，第3 个，第4 个，第5 个数据包，根据基于数据包伪包标识排序编码可知，伪包标识的排列为{2 ，4，3，1} ，因此将伪包标识2，4，3，1 依次添加到第1 个，第3 个，第4 个，第5 个数据包中，并以流的方式发送数据包。接收端根据数据包到达的顺序，获取数据包的大小为l1＜l3＜l4＜l5＜l，伪包标识排列 依 次 为{2 ，4，3，1} ，所 以 可 以 得 到K=0000，L-K=1011，因此si=00001011。

4 理论分析及实验结果

本节在理论上分析了2dCTC 的信道容量以及误码率，并通过实验将二维隐蔽时间信道与一维时间信道进行了对比。

4.1 理论分析

1）信道容量

在2dCTC中，假设n个数据包表示L比特的信息，则L和n满足公式：2L=n!mn，其中，m表示基于数据包大小变化编码中划分的区间的个数。因此，信道容量的上限为

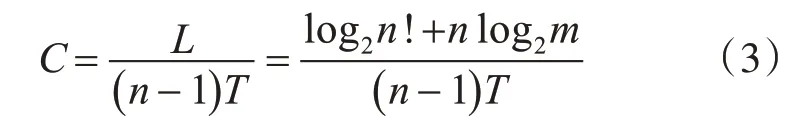
其中T表示发送相邻两个数据包之间的时间间隔。

2）误码率

由于网络噪声的存在，可能会对2dCTC的鲁棒性造成一定的影响，本文将2dCTC的网络噪声分为两类，第一类是仅仅破坏数据包的传输顺序，例如，数据包传输的时延和抖动，第二类是对传输中数据包数量造成影响，例如，数据包丢失，数据包聚合，数据包拆分和伪包的注入。

在我们先前的工作中，已经充分研究了这些网络噪声对于一维CTC所造成的影响［8，16］。我们在此基础上得出2dCTC的信道误码率。

由于数据包传输的时延和抖动的存在，接收端的两个相邻数据包之间的包间延迟Tr可以表示为式（4）：

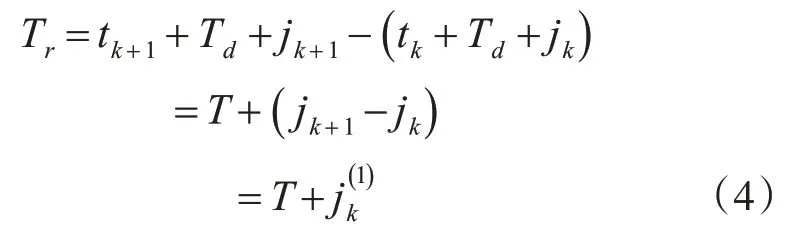
其中，Td为传输时延，jk表示时延抖动并且满足的随机正态分布，tk表示数据包发送的时刻，T表示发送相邻两个数据包之间的时间间隔。

假设Δ 为T的最小值，为了保持数据包的传输顺序，必须使得Δ+＞0，因为n个数据包包含n-1个包间间隔，所以传输误码率如式（5）所示：

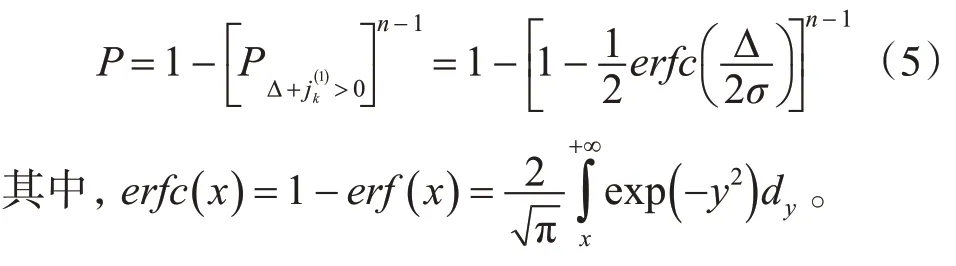
为了减小由数据包传输的时延和抖动带来的信道误码率，我们可以采取增加发送相邻两个数据包之间的时间间隔T的措施。

关于由数据包丢失，数据包聚合，数据包拆分和伪包的注入引起的信道误码率，不失一般性，假设λ表示数据包丢失的概率，μ表示数据包与其后续数据包聚合的概率，γ表示伪包注入的概率，以及ω表示数据包拆分的概率。在这些噪声下对信道误码率的期望可以表示为式（6）：

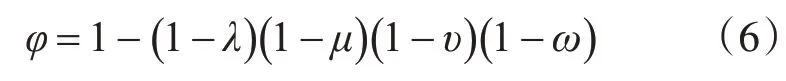
其中，φ的物理含义是至少发生一种此类噪声的概率。为了减轻数据包丢失，数据包聚合，数据包拆分以及伪包的注入对信道的负面影响，可以采取添加冗余信息，即在具有噪声的2dCTC下发送相同的消息k次，其中k≥1，且k∈N+。

4.2 实验结果

为了验证2dCTC的正确性和有效性，我们使用Python 实现了两台主机之间的隐蔽通信，通信协议为TCP。在这个实验中，数据包是通过Scapy 库生成的。本文选择400 个字节的文本文件作为隐蔽消息。数据包之间的时间间隔从5ms 依次递增到40ms。我们将2dCTC 的总时间消耗和容量分别与一维错序CTC、一维数据包大小CTC的总时间消耗和容量进行比较，其中容量的单位是bps，即在1s内传输的字节数。一维错序CTC 使用数据包真实ID 排列来表示消息，需要使用6个包表示8位。一维数据包长度CTC 是利用数据包大小的变化来表示消息，每个数据包表示1位，即8位二进制数需要8 个数据包。2dCTC 使用4 个数据包表示8 位。实验结果分别如图4（a）和图4（b）所示，实验结果表明，2dCTC与两种一维CTC相比，总时间消耗最小，信道容量也更高。

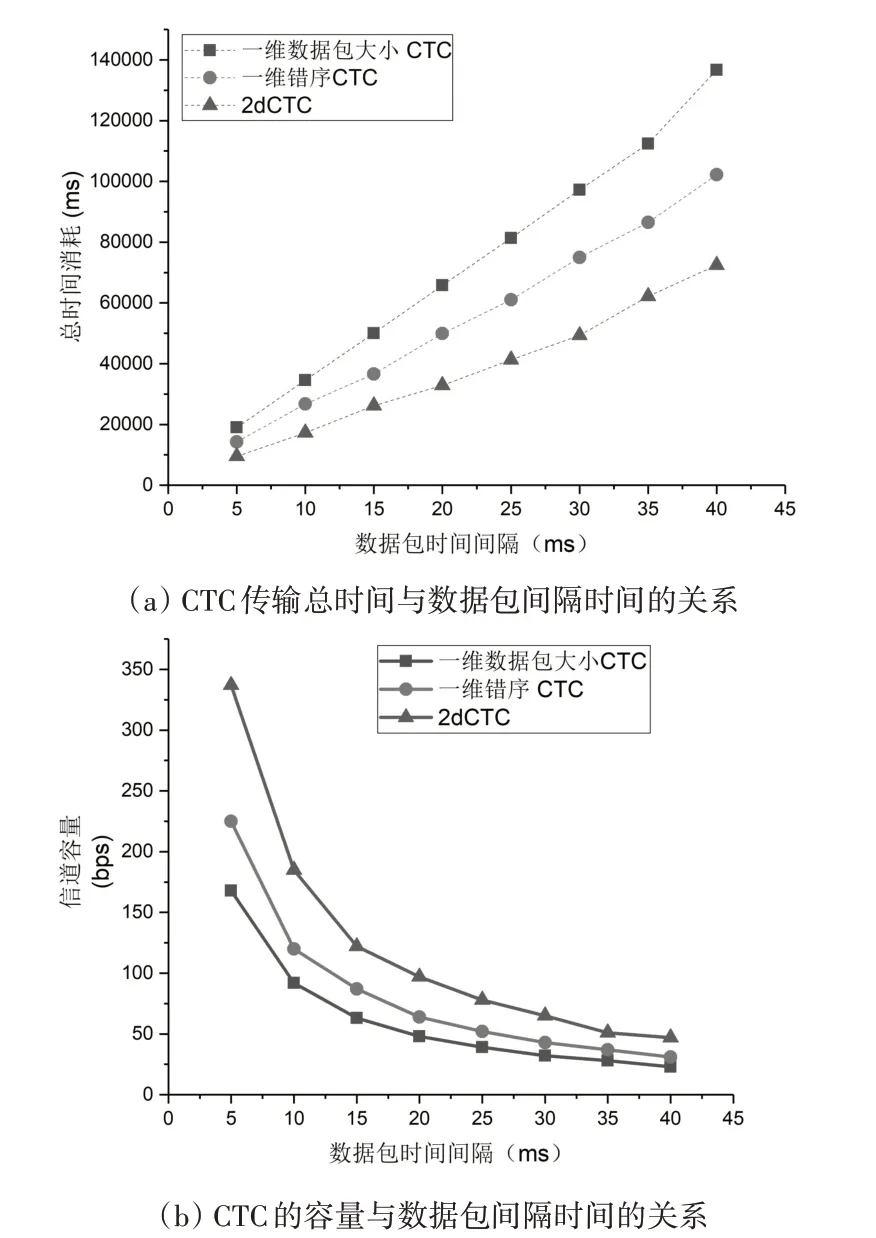
图4 实验结果

5 结语

为有效提高已有的隐蔽时间信道容量，本文首先提出了多维隐蔽时间信道的概念，作为应用设计并实现了一个二维隐蔽时间信道2dCTC。2dCTC采用数据包伪包标识排序和数据包大小变化相结合构造二维通信介质，使用康托展开进行编码与解码。理论分析和实验结果均表明2dCTC 在保证隐蔽通信效果的同时，信道容量得到了显著的提升。在下一步工作中，我们将设计具有更高维数的CTC，以进一步提高CTC的容量。