超长斜索三维气弹模型设计方法及其适应性研究
2021-12-22井昊坤李寿英陈政清
井昊坤,李寿英,陈政清
(1. 湖南大学风工程与桥梁工程湖南省重点实验室,湖南长沙 410082;2. 湖南大学土木工程学院,湖南长沙 410082)
缆索结构是大跨径斜拉桥、悬索桥的重要承重结构,其长细比大、质量轻、基频低、阻尼小,极易在多种荷载作用下发生大幅振动,影响缆索甚至全桥的的安全[1]。斜索振动主要包括内共振及参数振动[3]、风雨激振[4]、涡激振动[5]、干索驰振[7]和裹冰驰振[8]等。一般来说,斜索结构涡激共振风速低,仅对其疲劳寿命有一定的影响,但近年来,几座千米级主跨的斜拉桥拉索在高风速下发生了振幅明显的高阶涡振。MATSUMOTO 等[9]进行了高临界风速下的拉索涡振试验研究,发现当无量纲风速为60 时,可以激起拉索的8 阶振动,且设置端板可以抑制轴向流的影响。MATSUMOTO等[10]对全尺寸斜索进行现场实测,发现拉索发生7阶和8 阶的涡激振动。CHEN 等[11]对拉索进行了风洞试验,当风速为7.4 m/s时拉索发生7阶涡振,并发现风速越高拉索越容易发生多模态的振动。沈静思[12]发现苏通长江大桥上实测数据表明苏通长江大桥拉索高阶涡振可达到47 阶,并造成了套筒破坏、阻尼器漏油的现象。刘宗杰等[13]发现荆岳长江大桥JB01号拉索发生以12阶及14阶为主的多模态高阶涡振,JB02号拉索发生15阶、16阶和17阶涡振,并随着风速的增长最大出现28 阶振动。现场实测可观测到高阶涡激共振现象,但需进行详细的三维气弹模型风洞试验才能对其主要特征进行系统的研究。斜拉索或主缆均属于超细长结构,由于风洞尺寸的限制,在进行三维气弹模型设计时,存在长度和直径的几何缩尺比选择的矛盾。为此,DENG 等[14-15]提出一种新的超长索结构气弹模型设计方法,并在悬索桥竖向吊索尾流致振研究中得到了成功应用。但该方法应用到斜索结构时,可能会引起模型垂度和实际结构的差异,从而影响风洞试验结构的可靠性。基于上述讨论,本文研究了文献[14-15]的方法在超长斜索三维气弹模型设计时的适应性。以甬洲铁路某在建斜拉悬索协作体系桥梁边跨无吊索主缆为例进行三维气弹模型设计,系统研究了几何缩尺比对垂跨比、动力特性及涡振响应等的影响规律,确定了该主缆三维气弹模型的合理几何缩尺比,设计并制作了三维气弹模型。
1 斜索三维气弹模型相似关系
桥梁索结构属于超长细结构,进行三维气弹模型制作时,若以合适的索直径确定几何缩尺比,模型长度会远超风洞尺寸。若以合适的索长确定几何缩尺比,模型的直径会非常小。针对上述难点,以西堠门大桥吊索为工程背景,DENG 等[14]提出一种索结构模型缩尺新方法,即在对结构进行第1次缩尺后,在保证结构频率不变的情况下同时调整模型长度和张力大小,以实现第2次缩尺。利用此方法,设计了吊索的三维气弹模型并成功地进行了尾流致振风洞试验[15]。文献[14-15]所提方法的相似关系如表1 所示。其中,下标p 表示实际结构,下标l 表示经过初次缩尺的模型、下标s 表示经过第2 次缩尺的模型,λ1表示第1 次缩尺的几何缩尺比,λ2表示第2 次缩尺的长度缩尺比。后文将实际结构称为“原型结构”,将经过初次缩尺的模型称为“长模型”,将经过第2 次缩尺的模型为称“短模型”。

表1 三维气弹模型相似关系Table 1 Similarity criterion
2 三维气弹模型的垂跨比
将文献[13-14]方法应用到斜索模型中(这里的斜索主要包括斜拉桥拉索和无吊杆的悬索桥边跨主缆),由于在进行第2 次缩尺时张力和长度的调整比例不同,自重的作用下短模型的垂跨比与原型结构会有差别,可能会对试验结果产生影响。
本文以甬州铁路某在建斜拉悬索协作体系桥梁的边跨主缆为例,研究模型垂度对上述三维气弹模型的影响及适应性。该桥主桥采用主跨1 488 m 斜拉悬索协作体系桥。桥长2 664 m。主缆中跨矢跨比为1/6.5,主跨长度1 488 m。跨中纯悬索区段长452 m。梁上斜拉索、吊杆纵桥向间距14 或15 m,斜拉索横向间距63 m,吊杆横向间距27.5 m。本桥的立面示意图如图1所示。
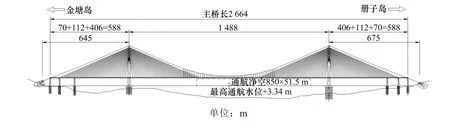
图1 桥梁立面图Fig.1 Elevation of bridge
该桥边跨主缆空间长度为727 m,外径0.804 m,提供刚度的核心面积为0.423 m2,单位长度质量3 940 kg/m,自重作用下垂度为8.39 m,垂跨比为1.15%,面内1 阶频率为0.194 Hz,面外1 阶频率为0.174 Hz。
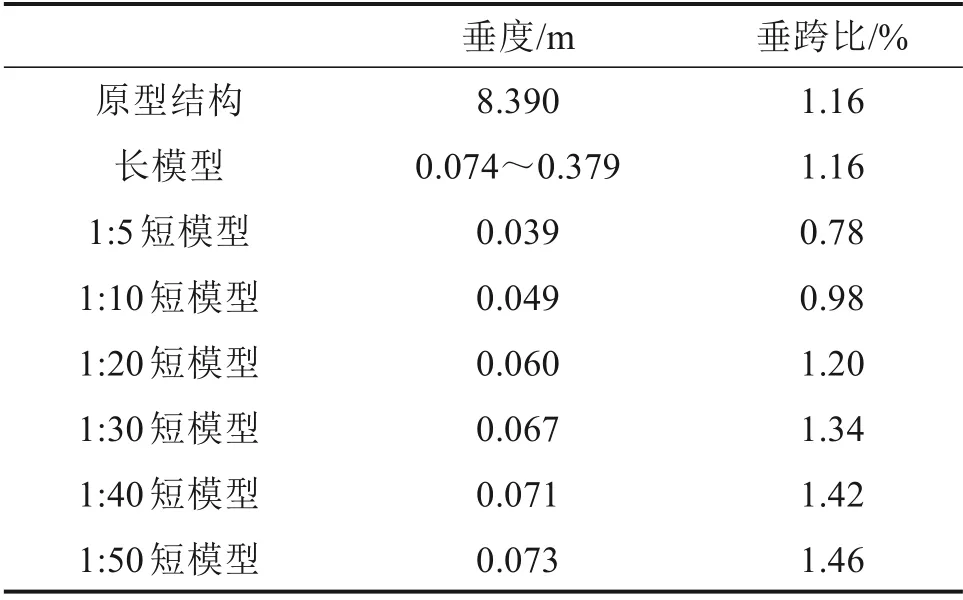
表2 3种模型的参数Table 2 Parameters of the three models
3 动力特性分析
3.1 气弹模型缩尺新方法对模型面外频率的影响
为探究气弹模型缩尺新方法对短模型动力特性的影响,利用ANSYS 有限元软件,采用Block Lanczos 法分别对几何缩尺比1:5 至1:40 下的短模型进行动力特性分析,并与长模型的结果进行对比。由于原型结构与长模型的频率严格满足频率比,因此在此处不对比原型结构的频率。图2为几何缩尺比λ1分别为1:10,1:20,1:30 及1:40 时5 m长短模型与长模型前30阶面外频率的对比。由图2可知,短模型的面外频率整体高于长模型的面外频率。
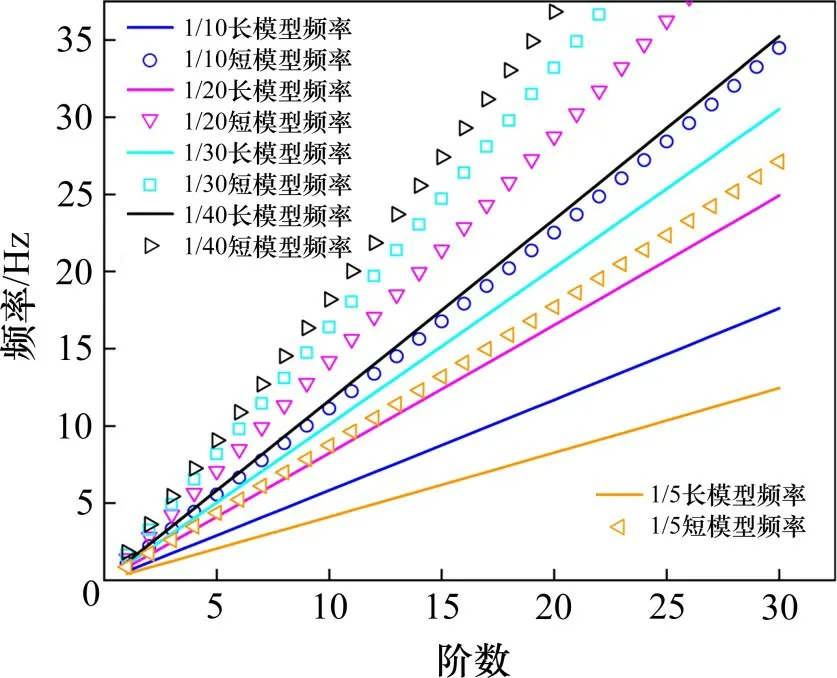
图2 短模型与长模型前30阶面外频率对比Fig.2 Comparison of frequencies outside the first 30 orders of short model and long model
3.2 气弹模型缩尺新方法对模型面内频率的影响
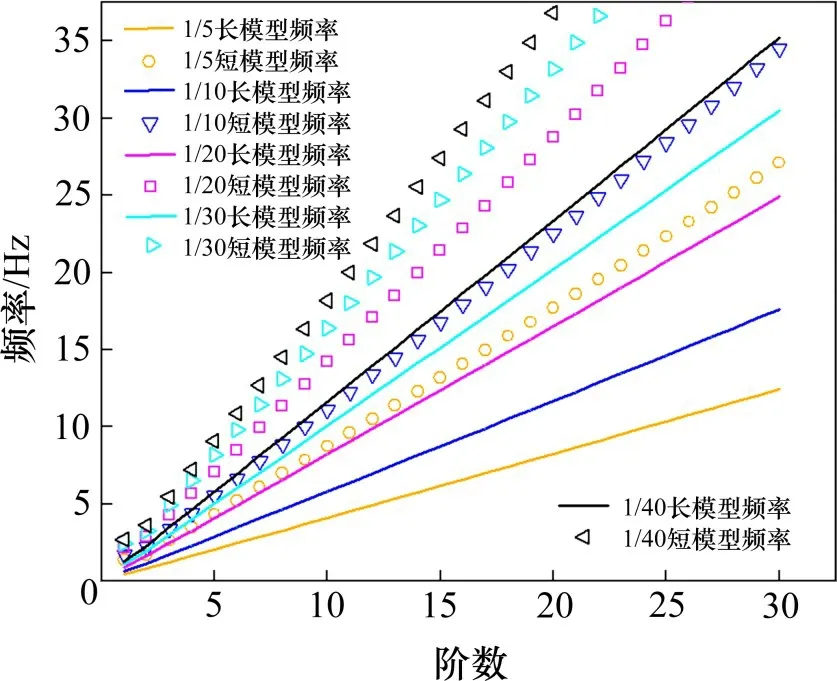
图3 短模型与长模型前30阶面内频率的对比Fig.3 Comparison of frequencies inside the first 30 orders of short model and long model
4 涡振响应分析
4.1 主缆的涡激振动三维理论模型
图4 为主缆结构的示意图,其中x轴沿主缆弦线方向,y轴沿主缆的垂度方向。主缆模型做出如下假定(16):1) 主缆本构关系满足胡克定律;2) 只考虑主缆的轴向刚度,不考虑主缆的抗弯刚度及抗扭刚度。
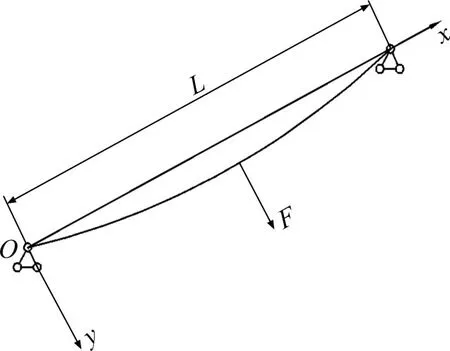
图4 边跨主缆模型Fig.4 Model of side span main cable
由于涡激共振指风速垂直于索面的特定情况,因此只考虑面内振动。在xy平面内主缆的振动偏微分方程为[16]:
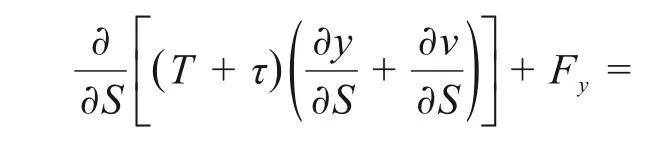
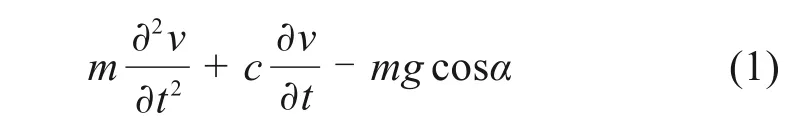
其中:T为主缆的张力;τ为振动中的附加张力;Fy为主缆面内的涡激力;c为主缆的面内阻尼系数;α为主缆两端连线与水平方向的夹角;S为主缆的曲线坐标;v为主缆沿y方向的振动位移。由主缆的静力构型及主缆微元的平衡方程可以得到:
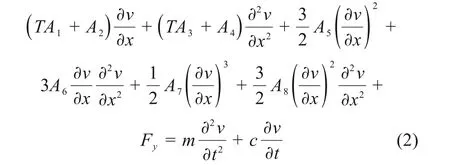
式(3)中的A1至A7为与静力构型有关的参数。表达式为:
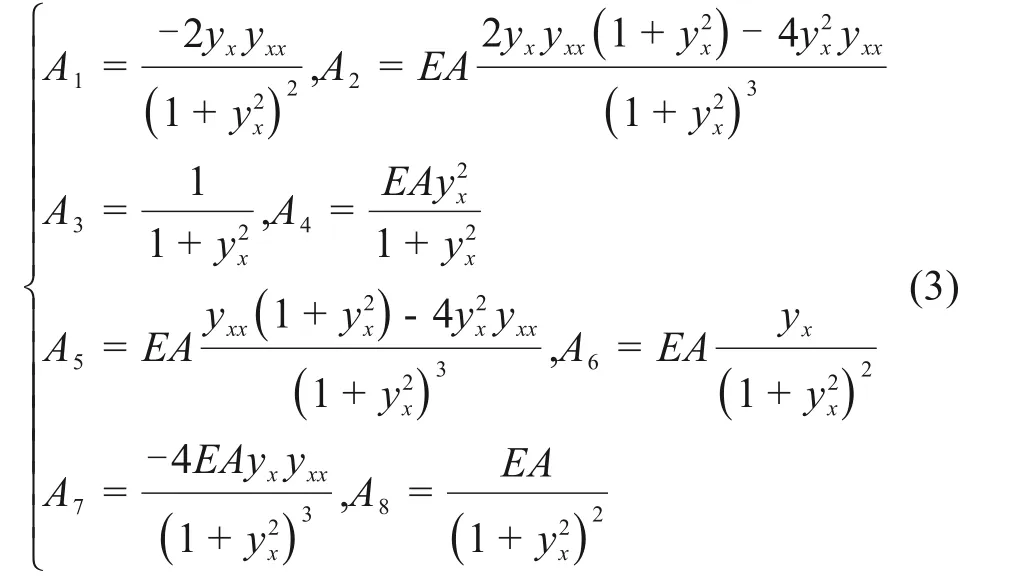
其中:yx为主缆的坐标对x的1 阶导数;yxx为主缆的坐标对x的2阶导数。
当主缆在风的作用下振动时,风在主缆表面形成交替脱落的漩涡,进而作用给主缆交替的涡激力。通常地,涡激力模型采用简谐力模型或经验非线性模型。此2种模型均含有大量参数需要通过试验进行识别,不利于数值模拟计算。因此,本文借鉴海洋立管计算涡振响应的尾流振子模型,即用范德波尔方程描述主缆的流固耦合运动,求解主缆的振动响应[17]。
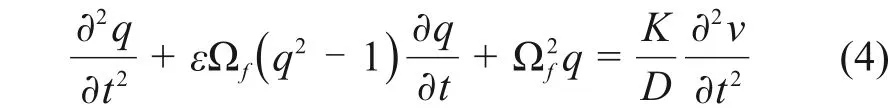
式中的流固耦合参数取用与海洋立管相关研究保持一致,其合理性已经过大量文献验证。其中:ε为非线性项参数,取值为0.3;K为结构与流体耦合参数,取值为12;q为脉动升力系数,初值为0.001;D为主缆的直径;Ωf为涡脱频率,Ωf=2πUSt/D。
式中:ri为机场优势度第i指标与旅游业发展水平的平均关联度;rj为旅游业发展水平第j指标与机场优势度的平均关联度。由此得出数据结果,可以分析机场与旅游业发展相互影响的主要因素。
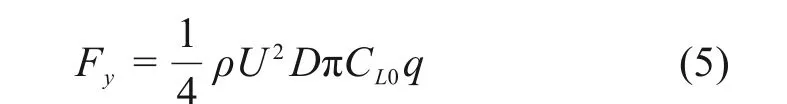
在计算得到脉动升力系数q后,可得到涡激力:
其中:ρ为空气密度,取值为1.225;U为来流风速;CL0为初始升力系数,取值为0.3。
4.2 数值求解
利用有限差分法对方程(2)进行离散,差分格式选用2阶中心差分格式。经过离散可得到主缆离散后的方程:
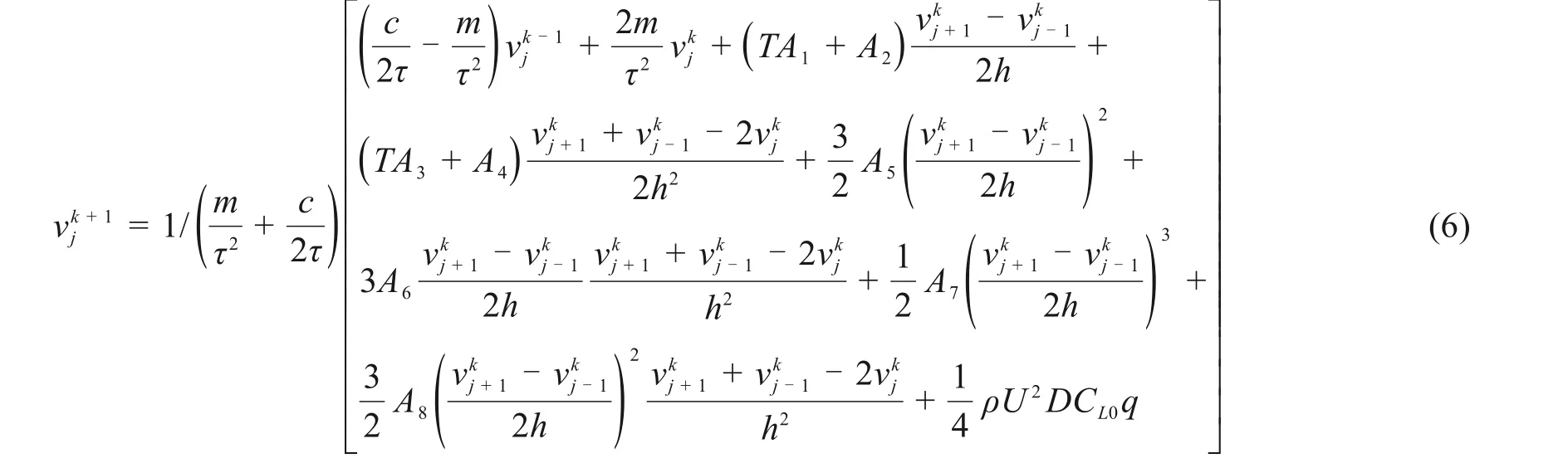
在求解尾流振子方程时,采用4阶龙格库塔法求解。

在解得尾流振子参数(8)和(9)之后,便可代入到主缆的振动方程(6)中循环求解直至得到最终结果。
4.3 程序合理性验证
利用苏通大桥NA30U 号拉索的实测数据验证理论模型。表3 为苏通桥NA30U 号索的参数。NA30U 号拉索所处A 类风场,在桥面风速为8.61 m/s 左右发生47 阶涡激振动, 振动主频为12.3 Hz,加速度幅值为30g,振幅约为0.005 m[12]。

表3 模型计算参数Table 3 Model calculation parameters
考虑风速沿拉索高度的变化。计算结果如图5所示。从图5 中可以看出:当桥面风速为7.85 m/s时拉索发生47 阶涡激振动,拉索的涡振响应幅值为0.011 m。频谱分析的结果表明拉索发生多模态振动,振动主频为12.5 Hz。由计算结果可知:1)程序计算苏通桥NA30U 号拉索发生47阶振动时的风速为7.85 m/s,略低于实测风速;2)程序计算的响应结果为0.011 m,比实测数据稍大。模拟与实测的差异主要原因为:1) 由于本文选用的涡激力模型为尾流振子方程,此方程多用于海洋立管的响应求解。当风作为介质使结构发生振动时,流固耦合参数取用与实际海洋立管计算中的流固耦合参数取用有些许差异。导致程序的计算结果与实际情况有微小差异。2) 实际拉索的振动环境较模拟更为复杂。总体而言,本文的程序与实测结果较接近,可以认为本文的程序编制合理。
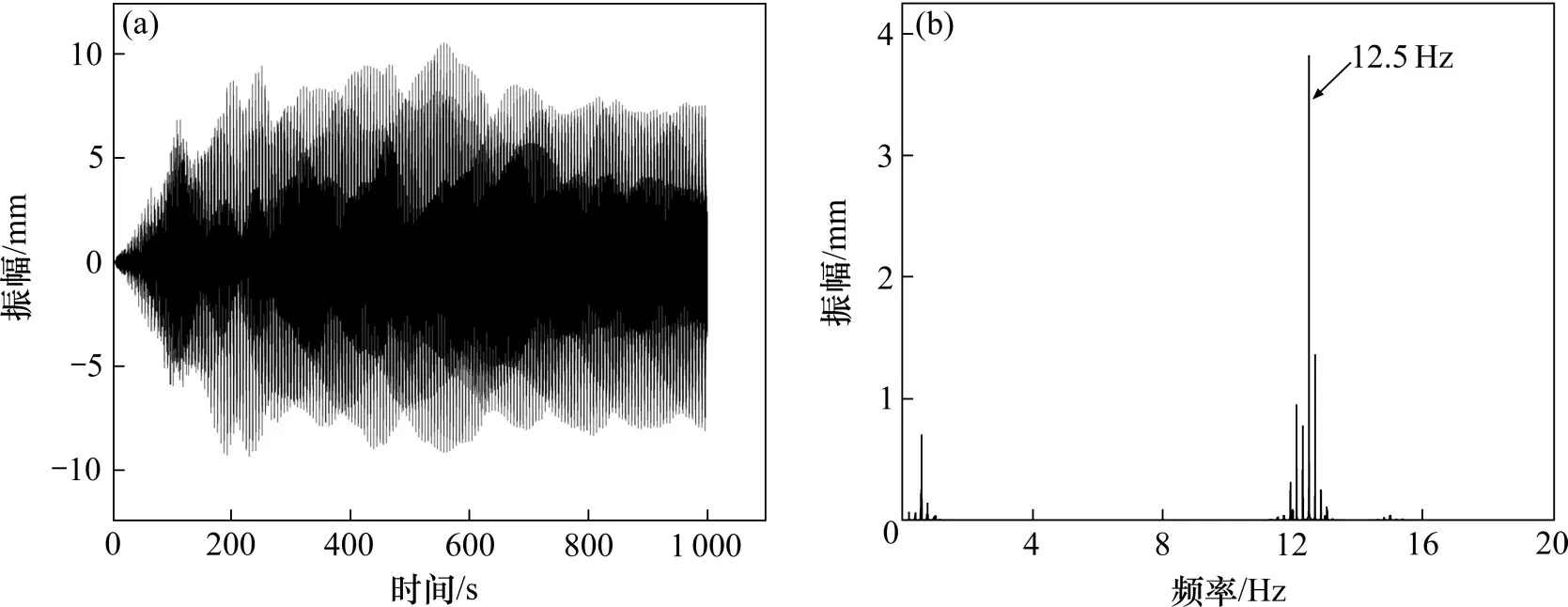
图5 程序计算桥面风速7.85 m/s时NAU30索结果Fig.5 Result of the NAU30 cable at the deck wind speed of 7.85 m/s
4.4 主缆风致响应计算
对原型结构进行均匀流场下的响应分析,发现原型结构在均匀风场作用下呈单模态振动。表4总结了原型结构的部分涡激振动计算结果。可以看到原型结构的涡振振幅约为0.04 m,无量纲振幅约为Y/D=0.05;无量纲风速U/fD约为5。
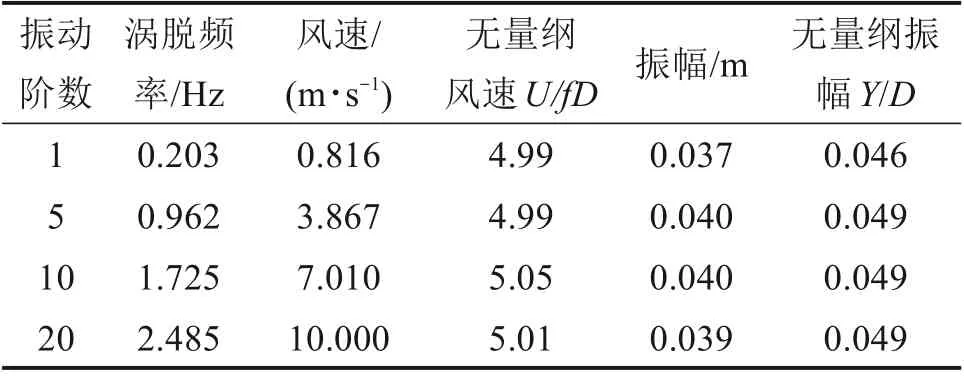
表4 原型结构均匀流场计算结果Table 4 Calculation results of uniform flow field of prototype structure
接着对长模型进行几何缩尺比λ1为1:5,1:10,1:20 及1:40 的涡振响应分析。图6 为长模型在几何缩尺比为1:5,1:10,1:20 及1:40 的涡振振幅随风速的变化规律。由图5 可知,几何缩尺比λ1为1:5,1:10,1:20 及1:40 时长模型的涡振振幅大致为0.008,0.004,0.002 和0.001 m,约等于原型结构的涡振振幅乘以几何缩尺比λ1。长模型的无量纲振幅约为Y/D=0.05。
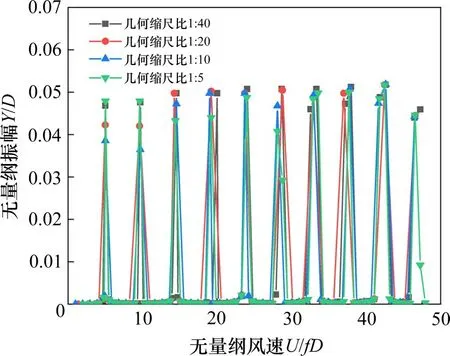
图6 长模型涡振响应计算结果Fig.6 Calculation results of vortex induced vibration response of the long model
图7 为不同几何缩尺比λ1与不同长度下短模型的涡振响应计算结果,并与长模型的涡振响应的计算结果对比。由图7可知,短模型在几何缩尺比大于1:20 时,无量纲振幅接近于0,表示在几何缩尺比大于1:20 时短模型难以发生振动。几何缩尺比在1:20 或低于1:20 时短模型发生涡激振动。短模型的响应无量纲振幅在0.05 附近,总体与长模型的响应结果接近。在相同长度下,几何缩尺比越小,短模型的无量纲振幅越小。在相同的几何缩尺比下,短模型的长度越长,无量纲振幅越小。总体而言,短模型的响应结果与长模型差距较小,可将几何缩尺比λ1定为1:20。
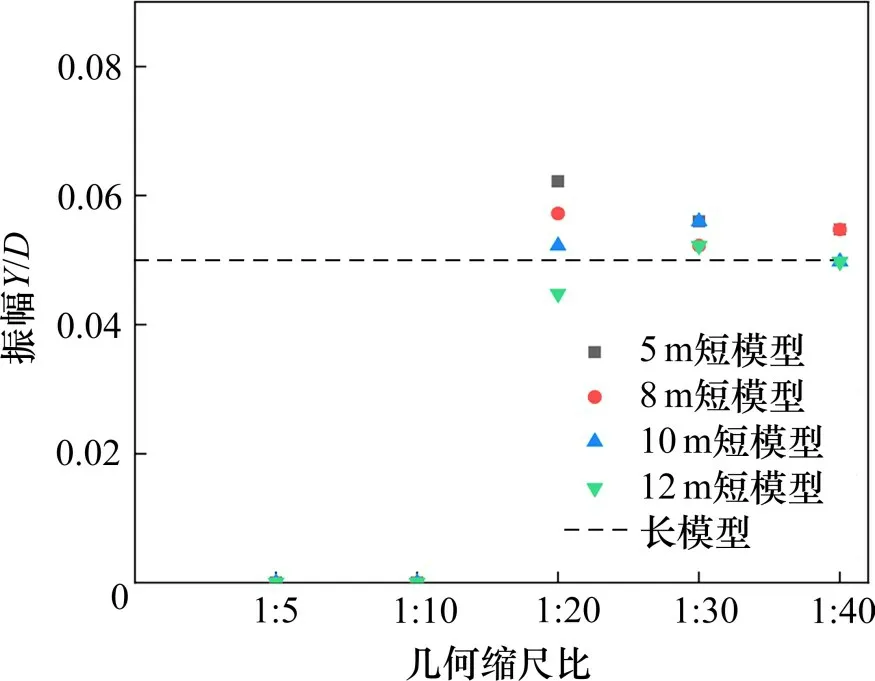
图7 短模型与长模型涡振响应结果对比Fig.7 Comparison of vortex induced vibration response between short model and long model
5 边跨主缆三维气弹模型设计
通过以上分析,并综合模型设计加工难度以及试验条件考虑,最终将模型的几何缩尺比λ1设计为1:20,模型长度设计为5 m,即长度缩尺比λ2为1:7.3。为保证模型可施加足够大的张力,采用5 m长直径0.002 m 钢丝提供抗拉刚度。模型重量由铜制外衣提供。外衣直径0.04 m,每段外衣由2 部分组成,通过内六角螺栓连接,确保外衣位置可调及外衣的多次使用。外衣通过内部挖空使气弹模型具有较低的阻尼比。每段外衣中点处设0.002 m平台以保证和钢丝连接。模型全长包含78段外衣,外衣设置间隔0.002 m。模型顶端与一个刚性柱连接,底端通过不锈钢花篮进行张力调节。图8为模型外衣示意图,图9为整体模型示意图。

图8 模型外衣示意图Fig.8 Model coat

图9 整体模型示意图Fig.9 overall model
图10 为短模型的面外自振时程及频谱图。图11 为短模型的面内自振时程及频谱图。由图10 及图11可知,模型的面内1阶频率为2.075 Hz,面外1阶频率为1.45 Hz。模型的频率与有限元分析得到的频率吻合良好。
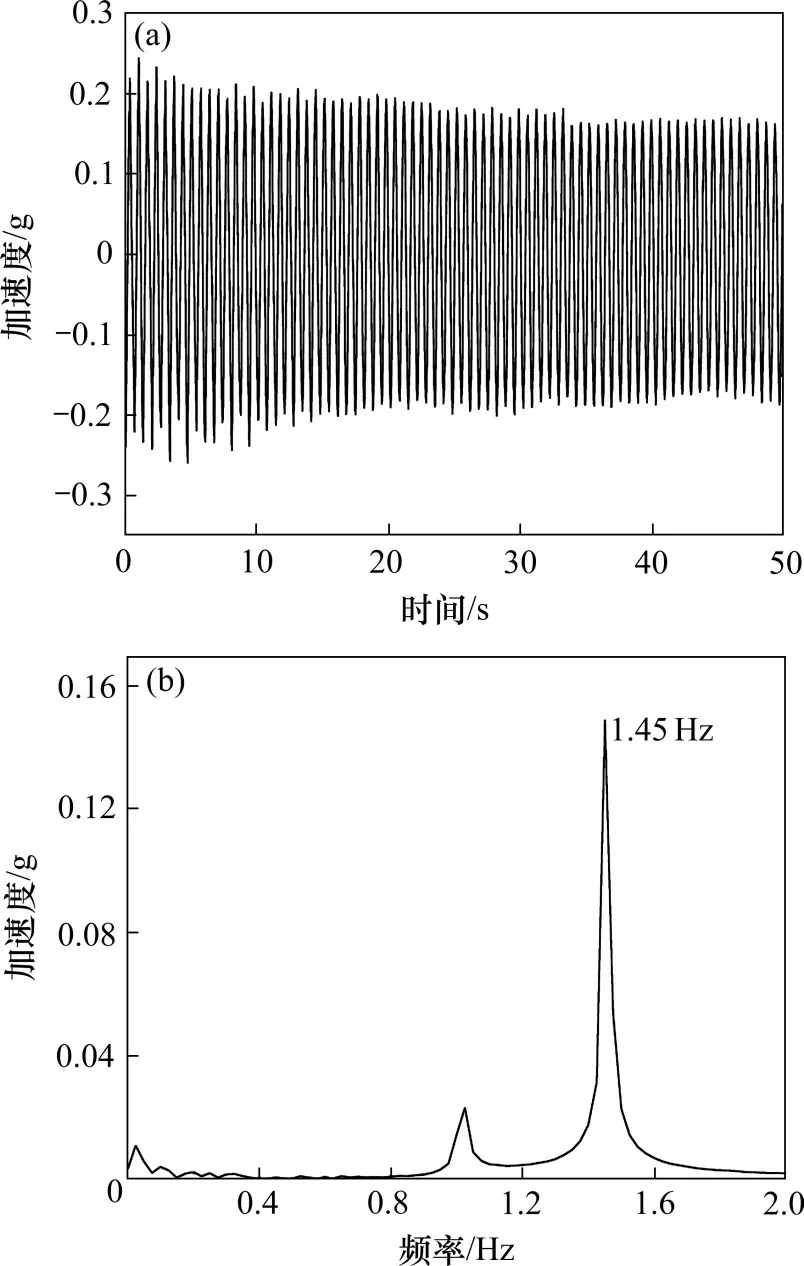
图10 面外自振时程及频谱图Fig.10 Time history and spectrum diagram of out-of-plane natural vibration
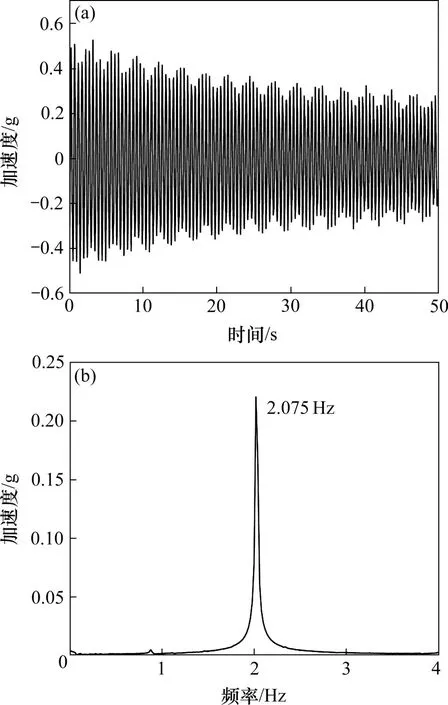
图11 面内自振时程及频谱图Fig.11 Time history and spectrum diagram of in-plane natural vibration
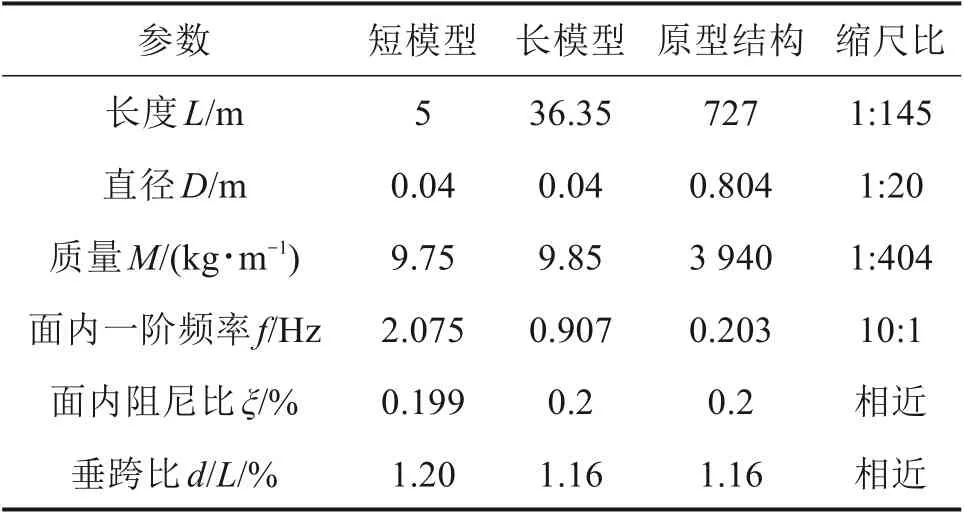
表5 模型计算参数Table 5 Model calculation parameters
6 结论
1) 该三维气弹模型设计方法使模型的无量纲垂度变大。模型设计的几何缩尺比λ1越小,模型的无量纲垂度越大。对于本文研究的边跨主缆,在几何缩尺比为1:20时垂跨比与原型结构接近。
2) 通过动力特性分析可知,该三维气弹模型设计方法得到的模型面内各阶频率高于长索模型,面外各阶频率同样高于长索模型。
3) 该三维气弹模型设计方法设计的模型涡振响应与长模型大致接近。与原型结构大致呈几何缩尺比的倍数关系。在相同的几何缩尺比下,模型的长度方向缩尺比λ2越大,模型的涡振响应越小。在相同的模型长度下,直径方向缩尺比(几何缩尺比)λ1越小,模型的涡振响应越小。
4) 采用该三维气弹模型设计方法,设计并制作了λ1为1:20,λ2为1:7.3的短模型。人工激励下得到的模型1阶频率与有限元模拟吻合良好,模型的阻尼比很低且与原型结构接近。
