基于小波神经网络的地铁基坑地表沉降随机预测
2021-12-22张蓓姚亚锋季京晨
张蓓,姚亚锋,季京晨
(1. 南通职业大学建筑工程学院,江苏南通 226001;2. 安徽建筑大学土木工程学院,安徽合肥 230022)
近年来,南通作为长三角核心城市,为适应区域经济一体化的格局,其轨道交通地铁建设正在紧张有序地开展[1-2]。根据前期的地质分析,南通地区属于长江下游三角洲冲积平原地貌,总体土质比较松软,含水率大,隧道施工时其基坑降水处理与沉降量分析对地铁隧道的变形和施工安全至关重要。以往基坑降水及沉降量预测方面的研究大多采用建立经验公式和数值分析的方法[3-6],未曾考虑到沉降量受降水因素、施工扰动和地下多变的岩土环境影响,存在一定随机性的问题,故造成计算结果与实际工程不符,可能导致安全事故发生。为此,在南通地铁软土层基坑降水试验的基础上,建立改进的小波神经网络对地铁基坑地表沉降进行随机预测,以期获得更为准确的基坑地表沉降数据,为地铁软土层基坑开挖工程提供有效基础资料[7-8]。
1 软土层基坑降水模型试验
1.1 基本工况
南通城市轨道交通1 号线1 期工程土建施工05标包含2 个地下车站、2 个盾构区间。其中某车站外包全长206.0 m,标准段宽20.7 m,端头井宽24.8 m,标准段深16.93~17.28 m,南端头井深18.92 m,北端头井深18.5 m;设4 个出入口,2 组风亭,主体及附属采用明挖顺筑法施工。车站横剖面如图1所示。

图1 某车站横剖面示意图Fig.1 Diagram of a station cross section
该车站位于南通市中央创新区,地貌类型属于长江三角洲冲积平原。车站基坑开挖以软土层工况为主,开挖现场如图2所示。为确保试降水试验结果的代表性,分别采集南通地铁车站基坑施工3 种典型软土层土样,其物理力学指标如表1所示。

图2 车站基坑Fig.2 Foundation pit of subway station

表1 软土层的力学指标Table 1 Mechanical index of soft soil layer
1.2 基坑降水三维模型
根据南通地铁基坑开挖软土层的水文地质情况,建立相应的地下水渗流三维模型[9-10]。采用有限差分法将渗流三维模型进行离散和网格划分,从而可以计算、预测抽水引起的地下水位的时空分布,如图3所示。按照工程经验,为消除边界对模拟结果的影响,将计算区域边界外扩约1 000 m。按照计算的平面范围、地层概化以及初始条件、边界条件,同时考虑抽水井、观测井、帷幕在离散模型中的空间位置,对计算区域进行离散,建立三维计算数值模型,如图4所示。其中,根据抽水井滤管位置及帷幕深度进行了分层。

图3 离散模型平面主要网格划分Fig.3 Main grid division in the plane of the discrete model

图4 离散模型三维划分Fig.4 3D division of discrete model
在封闭式围护条件下,根据建立的模型计算该车站主体基坑降水情况,60 d后水位降深曲线如图5所示。可见,坑内潜水含水层水位需满足降至基坑底以下1 m时,坑外水位最大降深0.55 m。

图5 水位降深等值线Fig.5 Contours of water level depth drop
2 降水引起地面沉降计算
按照《城市轨道交通岩土工程勘察规范》(GB50307—2012),地下水下降引起的土层附加荷载ΔP可按式(1)计算[11]:

式中:h1,h2分别为降水前和降水后水头高度;γw则代表水的重度。
根据叠加原理,地铁车站基坑降水所导致的地面总沉降量,可通过分层总和法来计算[12]。因此,结合土层附加荷载ΔP,车站基坑某软土层沉降量S可表示为式(2):

其中:φs为经验系数;U为土层的固结度;Si为土层i的沉降量;Ei为土层i的压缩模量;Hi为土层i的厚度。
将式(1)代入式(2),可得地层i降水引发地面总的沉降量计算表达式:

考虑降水的叠加影响,基坑降水运行60 d 后,在基坑周围布置相应的监测点,监测由降水引起的最大沉降。根据《建筑基坑支护技术规程》、《建筑基坑工程监测技术》等规范要求,结合南通地铁车站基坑施工的实际工况和软土层水文地质条件,综合设计监测点间距及监测点距基坑支护桩的距离,部分监测点位布置如图6所示。

图6 基坑地表沉降部分监测点位布置图Fig.6 Monitoring point layout of foundation pit settlement
选取距基坑支护桩距离分别为6,16,25,40和52 m的监测点D3-1,D3-2,D3-3,D3-4和D3-5为例,按式(3)获得的各层位节点沉降计算值与现场监测值对比结果如表2所示。
从表2可知,地表沉降计算值和监测值都随着距基坑支护距离的增大而减少,表明距离基坑支护桩越远,沉降越小。对比总沉降量计算值与监测值可以看出,沉降量的监测值与计算值总体变化规律相似,受降水因素、施工扰动和地下多变的岩土环境等影响,有时监测值高,有时计算值高,存在一定的随机性。为此,为准确有效地获得基坑地表沉降量来指导地铁施工,避免安全事故的发生,需借助人工智能算法并进行随机改进作为工具,以期更加准确预测地铁开挖中基坑地表沉降。

表2 沉降量计算值与监测值对比Table 2 Compare the calculated value of settlement with the monitored value
3 小波神经网络及随机改进
3.1 小波神经网络
小波神经网络将小波强大的变换能力和人工神经网络的非线性规划进行了有机融合,受到广大工程界的青睐[13]。该智能算法将传统的人工神经网络中的神经元替换为基于小波分析的小波元,通过数学变换,将输入层到隐含层的权值变换为新的伸缩参数,隐含层的临界值变换为新的平移参数。其结构如图7所示[14]。

图7 小波神经网络Fig.7 Wavelet neural network
网络图中隐含层的激励函数可表示为:
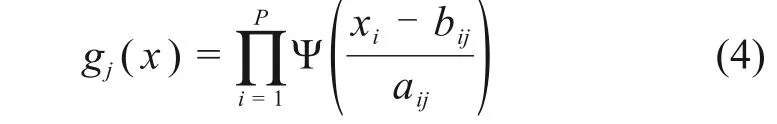
其中:Ψ表示相应的小波运算;X为网络输入量;i代表网络中不同的输入小波元;j为网络中间层代码;aij和bij代表变换后新的伸缩和平移参数。
因此,小波神经网络的输出函数可表示为:
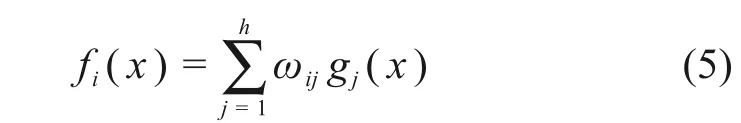
式中:h为小波网络的层级数;ωij表示输出权重。
3.2 随机改进
传统的小波网络的函数和参数虽然都经过小波的数学变换后获得,但变换方法单一固定,可能无法适应工程实际的复杂多变的工况,同时也容易导致算法逼近速率降低[15],为此考虑从以下2方面对小波神经网络进行随机改进。
1) 为解决逼近速率问题,改进后的激励函数和输出函数分别为:式中:d表示输出值的数学期望;yi表示实际的网络输出值。

2) 同时,用梯度下降的方法,对伸缩参数和平移参数进行改进:

式中:ηa和ηb为各自的训练因子,Δaj(t),Δbj(t)分别伸缩参数和平移参数的为梯度指标。改进后2个参数的梯度指标分别通过式(11)和式(12)获得。

通过以上2方面的改进,随机小波神经网络可从整体上解决逼近速率的问题,同时也能适应复杂多变的随机工况,成为人工智能预测的有效工具。
4 随机小波网络基坑地表沉降预测模型
4.1 输入量与输出量的确定
前期南通地铁软土层基坑降水模拟发现,基坑降水引发的沉降受降水因素、施工扰动和地下多变的岩土环境等影响,具有一定的随机性。结合式(3)可知,沉降量与水位降深、土层的压缩模量、土层厚度、固结度和监测点的方位等主要因素有关,故将以上5个参数作为随机小波网络基坑地表沉降预测模型的输入量。
文中旨在较准确获得地铁车站开挖过程中基坑降水后的沉降量,防止施工安全事故发生。为简化模型,故将南通地铁软土层中基坑降水引起的总沉降量作为随机小波网络基坑地表沉降预测模型的输出量。
4.2 隐含层单元的确定
在小波神经网络中,隐含层单元数的选择也很关键。隐含单元数过少,整个网络不能很好地信息处理;隐含单元数过多,会直接导致结构冗余和陷入局部最小。为均衡两者关系,通常采用下式确定小波神经网络的隐含单元数[16]。其中:Z为隐含层单元数;n为网络输入量个数;m为网络输出量的个数。

结合基坑地表沉降预测模型的输入量和输出量的个数,将n=5,m=1 代入式(11),可得z=3.78,故随机小波网络基坑地表沉降预测模型的隐含层单元数设定为4为宜。
5 工程实例验算
为验证随机小波网络基坑地表沉降预测模型的适用程度,选取南通地铁2号线某车站基坑典型软土层工况作为验证算例。将不同的水位降深、土层的压缩模量、厚度、固结度和监测点方位下的沉降预测模型值与基坑降水运行60 d 后现场监测值进行比较,预测模型中设训练效率因子ηa=0.35,ηb=0.21;网络权值ωij和ωjk初值分别为4.12和3.96,伸缩参数初值aj=1.6,平移参数初值bj=0.8,结果如表3和图8所示。

表3 基坑地表沉降随机模型预测结果Table 3 Prediction results of random model for foundation pit surface settlement

图8 模型预测值、公式计算值与监测值对比Fig.8 Comparison of model predicted value,formula calculated value and monitoring value
根据上述实例结果,本文优化的随机小波网络模型能使基坑地表沉降预测值与具体工程实测值基本吻合,误差均小于±8%。再将各监测点的模型预测值、现场监测值和传统公式计算值进行对比,可知随机小波网络基坑地表沉降模型的预测值比传统公式的计算值更接近现场监测值。由此可见该预测模型可作为南通地铁施工中基坑地表沉降预测的有效工具。
6 结论
1) 软土层基坑降水模型试验发现:降水引发的基坑地表沉降随着监测点距基坑支护桩距离的增大而减少,工程中距离支护桩越远,沉降量越小。同时,在不同的监测点沉降量的监测值与公式计算值总体变化规律相似,但受降水因素、施工扰动和地下多变的岩土环境等影响,存在一定的随机性。
2) 利用权值参数对小波神经网络的激励和输出函数进行修正,利用梯度下降的方法对伸缩和平移参数进行优化。在此基础上,以水位降深、土层的压缩模量、厚度、固结度和监测点方位为输入参数,基坑总沉降量为输出参数建立改进后的随机小波网络基坑地表沉降预测模型。该随机模型可作为南通地铁施工中基坑地表沉降预测的有效工具。
3) 工程实例表明,改进后的随机小波网络模型能使基坑地表沉降预测值与具体工程实测值基本吻合,误差均小于±8%。而且模型的预测值比传统公式的计算值更接近现场监测值。
